基于变换热力学的三维任意形状热斗篷设计∗

夏舸 杨立 寇蔚 杜永成

(海军工程大学动力工程学院,武汉 430033)

基于变换热力学的三维任意形状热斗篷设计∗

夏舸 杨立†寇蔚 杜永成

(海军工程大学动力工程学院,武汉 430033)

(2016年11月22日收到;2017年3月9日收到修改稿)

在变换热力学的基础上,通过坐标变换的方法,推导出三维任意形状热斗篷导热系数的通解表达式,并进行了全波仿真验证.结果表明∶热流均能绕过保护区域流出,保护区域的温度保持不变,而且热斗篷外的温度场并没有破坏,具有很好的热保护和热隐身的效果.这一方法把变换热力学从二维拓展到三维,具有普遍的适用性.同时,这种技术为热流流动路径和目标温度场的控制奠定了理论基础,在微芯片、电动机的保护以及目标热隐身上有潜在应用.

∶变换热力学,热斗篷,三维任意形状,温度场

PACS∶44.10.+I,05.70.—a,81.05.Xj,07.05.TpDOI∶10.7498/aps.66.104401

1 引 言

2006年,Pendry等[1]和Leonhardt[2]从麦克斯韦方程的形式不变性出发,通过坐标变换的数学方法推导出具有各向异性特性的人工超材料的参数,使得电磁波按照预先设定的路径传播,从而达到电磁隐形的目的.从此,这种控制电磁波传播的理论方法引起了广大学者极大的关注,并逐渐发展成为变换光学的一般理论[3−5].变换光学理论不但可以应用于制作隐形器件[6,7],还能用来设计波束集中器[8,9]、完美透镜[10]、波束旋转器[11]以及指向性天线等[12].后来,人们又把光学变换理论的思想应用到声波[13,14]、物质波[15]、弹性波[16]和热流[17]的传播路径设计上.

与电磁波、声波以及弹性波等不同,热流并不是一种波,仅仅是从热端到冷端的流动[18].基于导热方程的不变性,通过构造出特定的热物性参数,可以实现对热流传递方向的控制与利用,满足工程实际应用.2008年,Fan等[19]通过利用分级材料,设计出球形和椭球型热隐身衣,并对其进行了仿真验证,这是变换热力学理论第一次被提出并验证.后来,Guenneau等[20]提出一种通过20层同心的各向同性材料构建出二维非稳态热斗篷和热聚集器的方法.在此基础上,Schittny等[21]利用铜片和聚二甲基硅氧烷两种材料交替排列构建10个等厚度的环,从实验上验证了二维热斗篷的隐身效果.2014年,毛福春等[22]在变换热力学的基础上,设计出具有非共形任意横截面的柱形热斗篷热导率的表达式,并通过COMSOL Multiphysics仿真验证了热斗篷对隐身区域具有热保护的功能.同时,秦春雷等[23]将连续介质力学的方法引入热力学中,数值求解连续介质位移的拉普拉斯方程获得封闭曲线内场的形变信息,进而可以计算任意形状的热斗篷的材料参数.

热斗篷由于其特殊的导热系数分布使得热流绕过保护区域,这一特质使其能够应用于计算机芯片、高速电动机的热保护以及军事目标的伪装中.然而,目前对热斗篷导热系数研究大多数局限在二维空间里,而对于三维形状热斗篷也基本局限于球体、椭球体以及柱体等规则共形热斗篷的研究.而在实际应用过程中,这些简单规则的三维模型往往不能满足要求.而对基于拉普拉斯方程的热斗篷研究方法由于其介质参数全部是数值结果,在精确提取参数进行材料实现时困难较大,不利于在工程上实现.因此,本文基于变换热力学的方法,推导出三维任意形状热斗篷的导热系数的通用表达式,并通过全波仿真分析球体、椭球体、共形任意形状热斗篷和非共形任意形状热斗篷,验证了表达式的正确性以及热斗篷的隐身和保护双重功能,这些结果为三维热斗篷热物性参数的隐身设计和改进奠定了理论基础.

2 理论和方法

热传导是物体只依靠微观粒子(分子、原子或者自由电子)的热运动产生的热量传递的现象.在无内热源情况下,稳态热传导方程的一般形式可以写成[24]

式中,T表示区域温度,λ表示导热系数,∇表示梯度算符.

与基于麦克斯韦方程的变换光学类似,根据变换热力学理论[20],由于方程(1)具有形式不变性,导热方程在变换空间可表示为

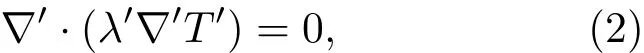
式中,T′和λ′分别表示物体在变换空间中的温度和导热系数,∇′表示变换空间中的梯度算符.变换空间与原空间介质的导热系数的关系为[25]

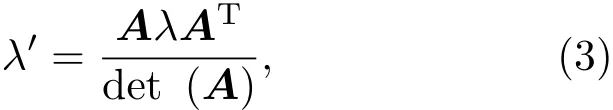
式中,A为变换空间与原空间之间的雅克比矩阵,ATAT是A的转置矩阵,det(A)为矩阵的行列式的值.不同坐标系下的雅克比矩阵是不同的,在球坐标系下的雅克比矩阵∶

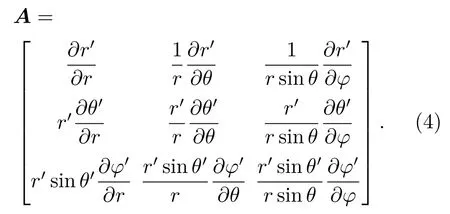
对于三维热斗篷,假设内外边界分别为r=R1(θ,φ)和r=R2(θ,φ), 为了实现对保护区域的完美隐形,把0＜ r＜ R2(θ,φ)区域压缩到R1(θ′,φ′) ＜ r ＜ R2(θ′,φ′)区域, 得到保护区域r ＜ R1(θ′,φ′). 区域r ＞ R2(θ,φ) 保持不变. 因此变换方程如下[22]∶

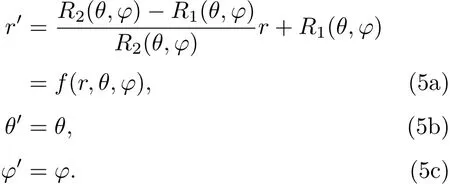
把(5)式代入(4)和(3)式,经过推导可以得到所需变换空间的导热系数为

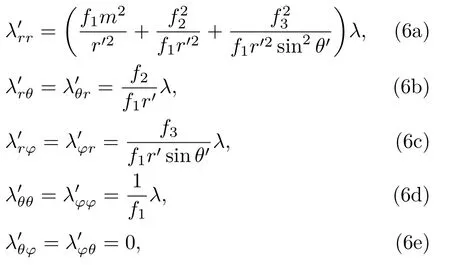
式中

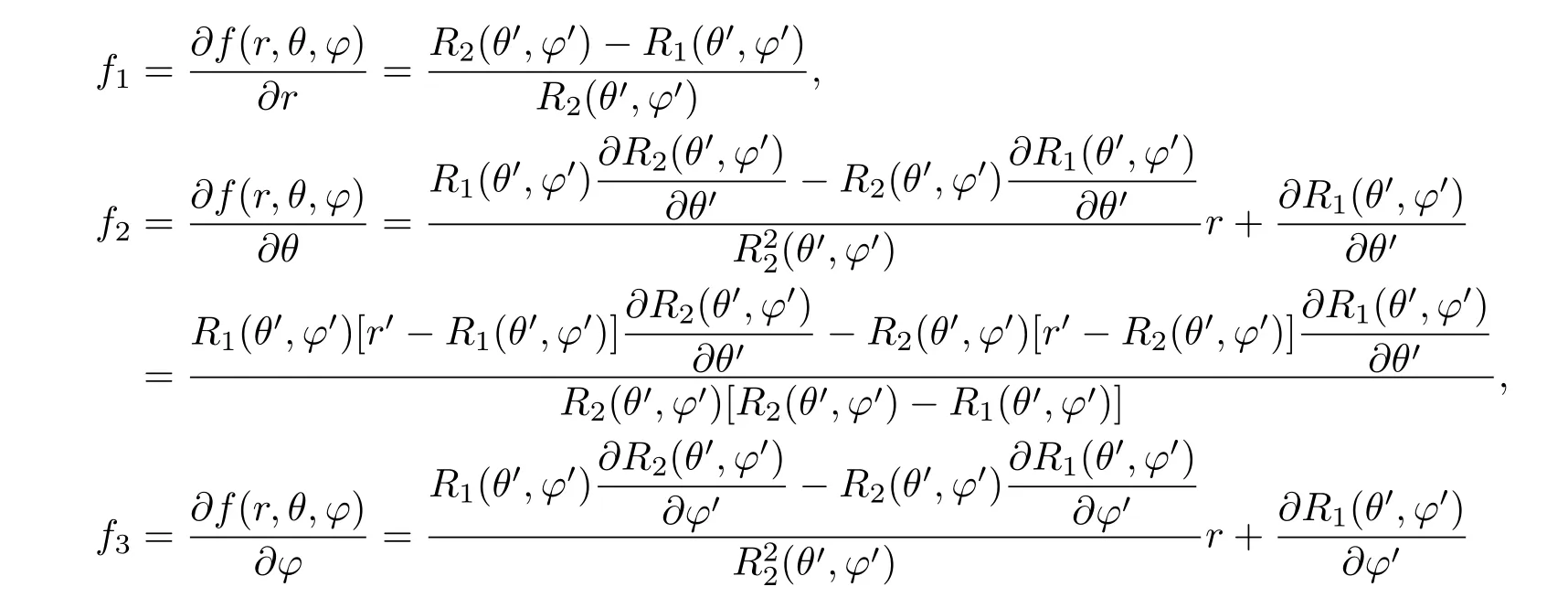
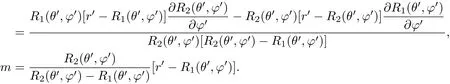
将球坐标系下的材料导热系数转换为材料在笛卡尔坐标系下的导热系数,具体转换关系如下∶

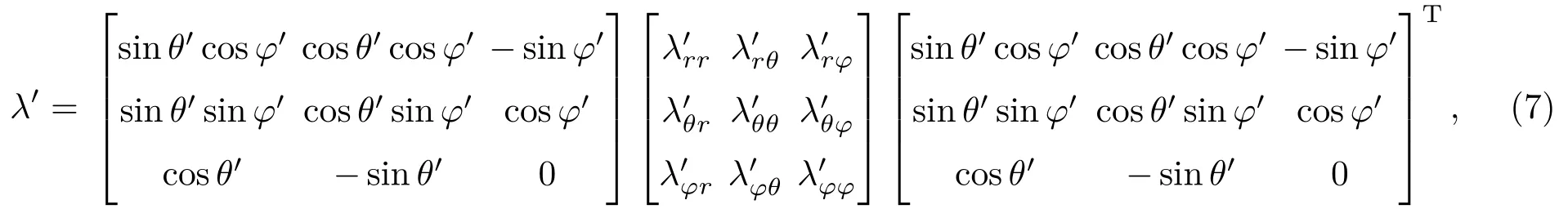
化简得到

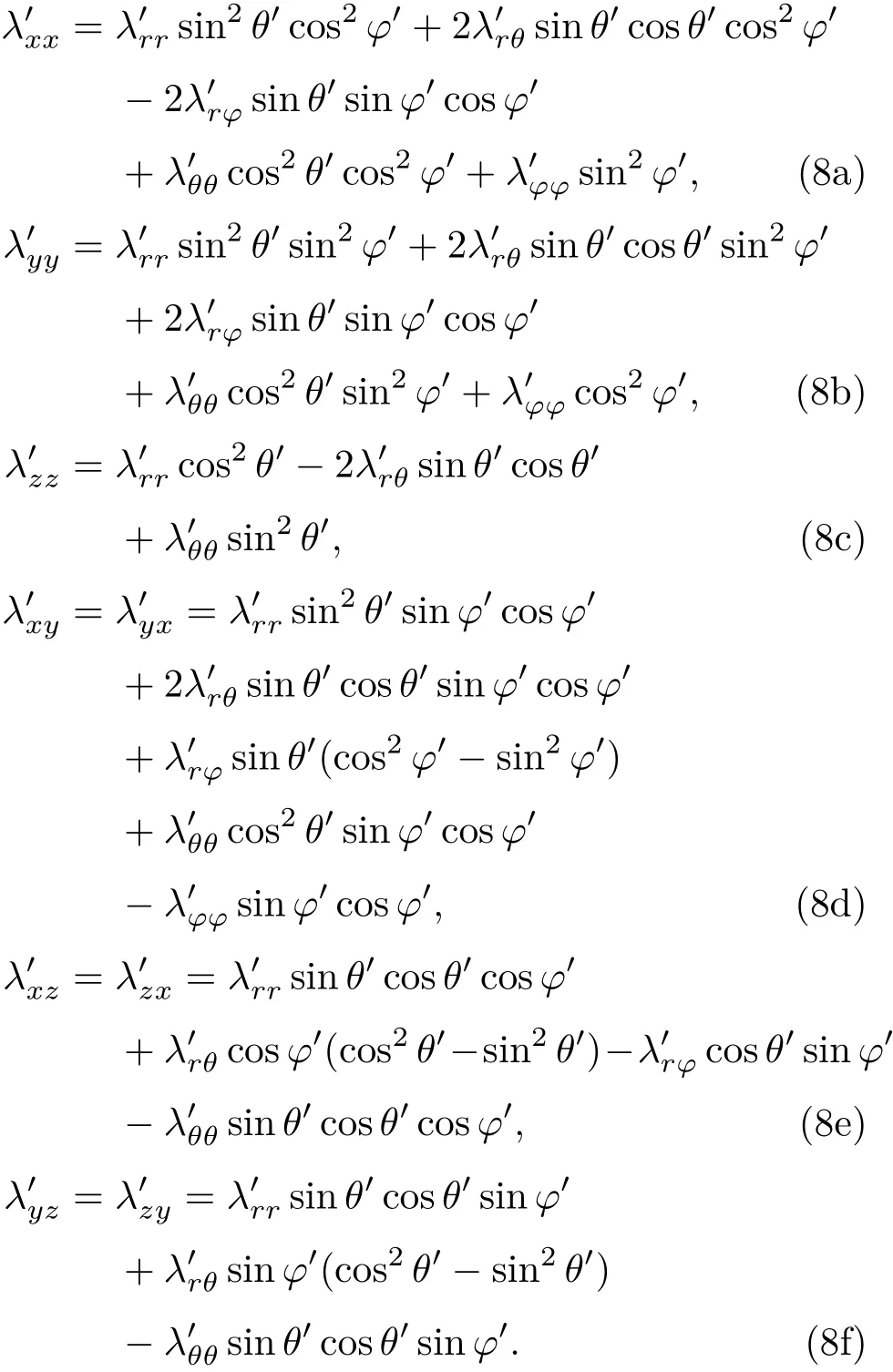
根据(6)和(8)式即可得到内外边界为r=R1(θ′,φ′)和r=R2(θ′,φ′)的三维任意形状热斗篷导热系数的一般表达式.当消去θ′,简化为二维任意形状热斗篷时,与参考文献[22]一致.

3 仿真验证与分析

为了验证热斗篷导热系数表达式的正确性,本文采用有限元仿真软件COMSOL Multiphysics进行全波仿真.假设整个区域为一个1 m×1 m×1 m的空间,前后左右四个面保持绝热,上下两个面分别保持恒温,上面为高温保持在400 K,下面为低温保持在300 K;在被保护的隐形区域和热斗篷外的区域的材料为铜.在常温下铜的各项基本参数如下∶密度ρ=8960 kg/m3,导热系数λ=400 W/(m·K),常压热容Cp=385 J/(kg·K).在热斗篷区域,材料的导热系数λ′由(6)式和(8)式计算得出.

3.1 共形热斗篷

热斗篷区域的形状主要取决于内外边界函数的选取, 当外边界函数R2(θ′,φ′)与内边界R1(θ′,φ′)的比值为常数, 且r=R1(θ′,φ′)全部区域都在r=R2(θ′,φ′) 内部时, 则此为共形热斗篷.先取典型案例球体热斗篷作为分析对象,假设内球半径R1(θ′,φ′)=0.2 m, 外球半径为R2(θ′,φ′)=2R1(θ′,φ′)=0.4 m.

图1(a)—(c)为稳态球体热斗篷的模拟结果.从图1(a)和图1(b)可以看出,未加热斗篷时,所有等温面保持平行,与热流方向垂直.在加入热斗篷后,进入热斗篷之前所有的等温面保持平行,与未加入斗篷的情况一样.在进入热斗篷区域后,等温面开始发生变化从而影响整个温度场的分布,当等温面进入上半球壳热斗篷时,由于球壳内不同位置导热系数不同,越接近内球,径向导热系数越小,所以等温面像一顶帽子扣在内球之上,而下半球壳热斗篷情况与上半球壳正好对称.内球并没有任何热流穿过,说明内球保护区域的温度保持一致.当等温面出了热斗篷后,又恢复了平行状态.图1(c)为yoz平面上的热流与等温线分布图.热流从上到下均匀流动,在斗篷外侧,等温线间距大小一致,热流密度处处相等.热流能够平滑地绕过内部的保护区域而对斗篷外部区域不产生任何影响,这与文献[26]结论一致.由于内球保护区域目标的存在不会破坏斗篷外部的温度场,同时外部热流无法进入目标的区域,从上表面方向上无法发现目标的存在.因此,此球体热斗篷具有较好的热保护和热隐身效果.

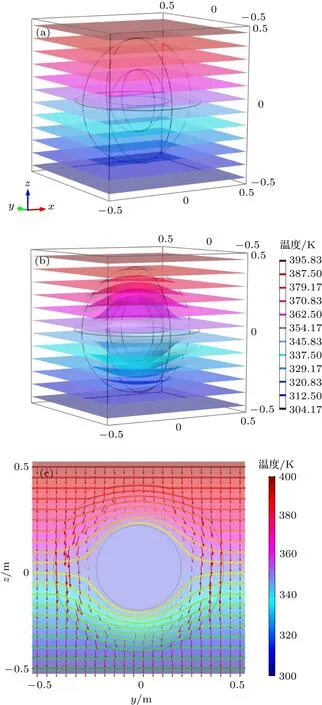
图1 (网刊彩色)球体热斗篷(a),(b)等温面分布图;(c)yoz平面的等温线和热通量分布Fig.1.(color online)Spherical thermal cloak:(a),(b)Distribution of isothermal surface;(c)isotherms and heatflux profile in the yoz plane.

图2和图3为三维椭球和共形三维任意形状热斗篷的仿真结果.椭球的球坐标方程为

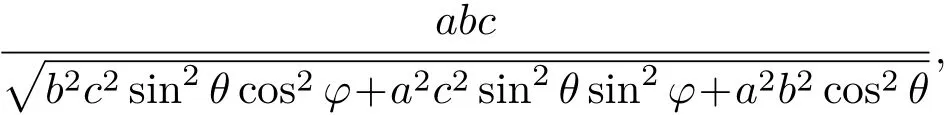
共形三维任意形状热斗篷的仿真参数方程为

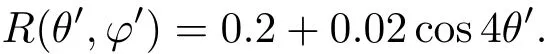
仿真时,R1(θ′,φ′)= R(θ′,φ′),R2(θ′,φ′)=1.5R1(θ′,φ′), 由图3 的仿真结果可以看出, 该热斗篷同样具有热保护和热隐身双重功能.

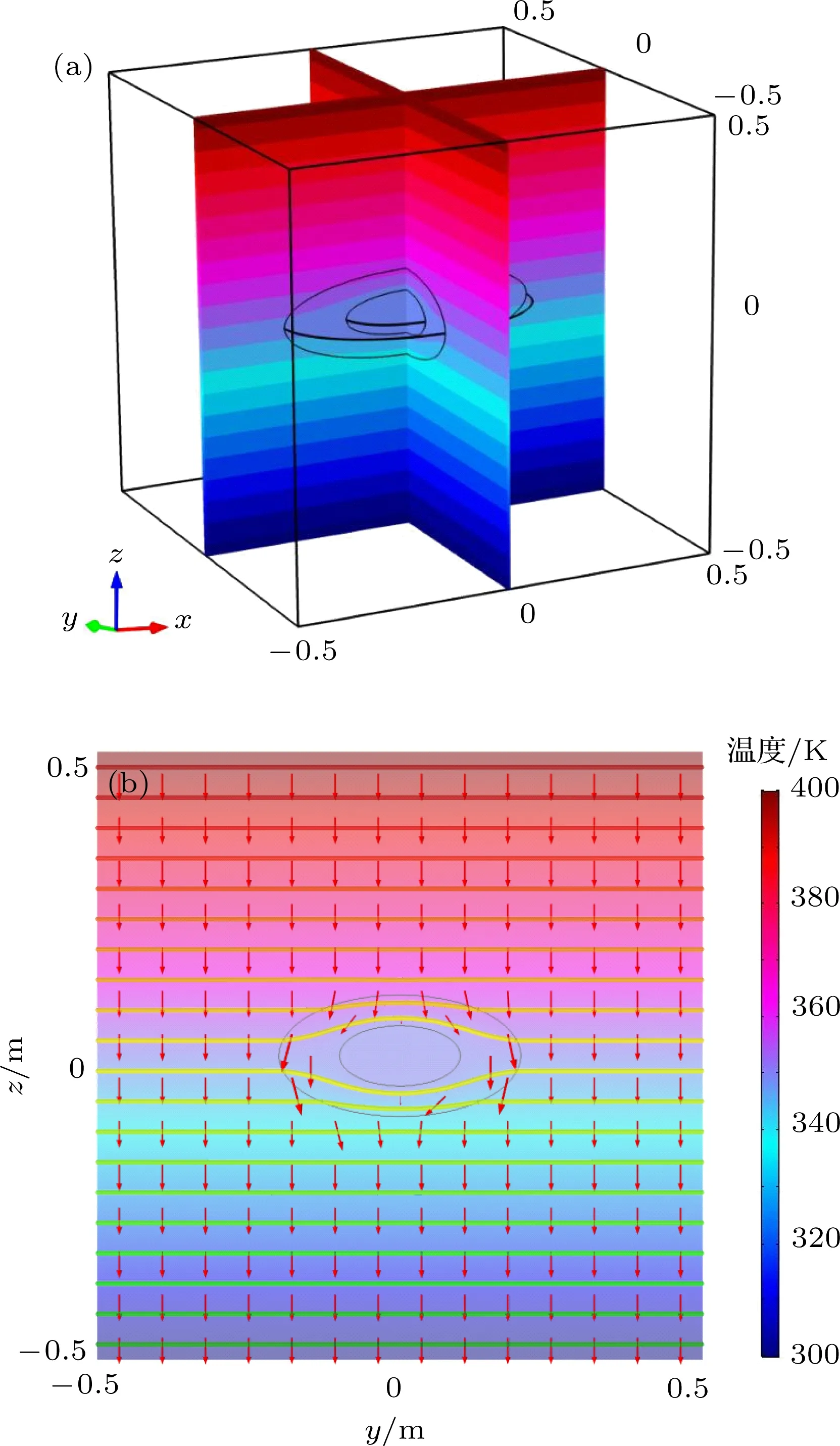
图2 (网刊彩色)椭球热斗篷 (a)三维空间温度分布;(b)yoz平面的等温线和热通量分布Fig.2. (color online)Ellipsoidal thermal cloak:(a)Three-dimensional temperature distribution;(b)isotherms and heatflux profile in the yoz plane.

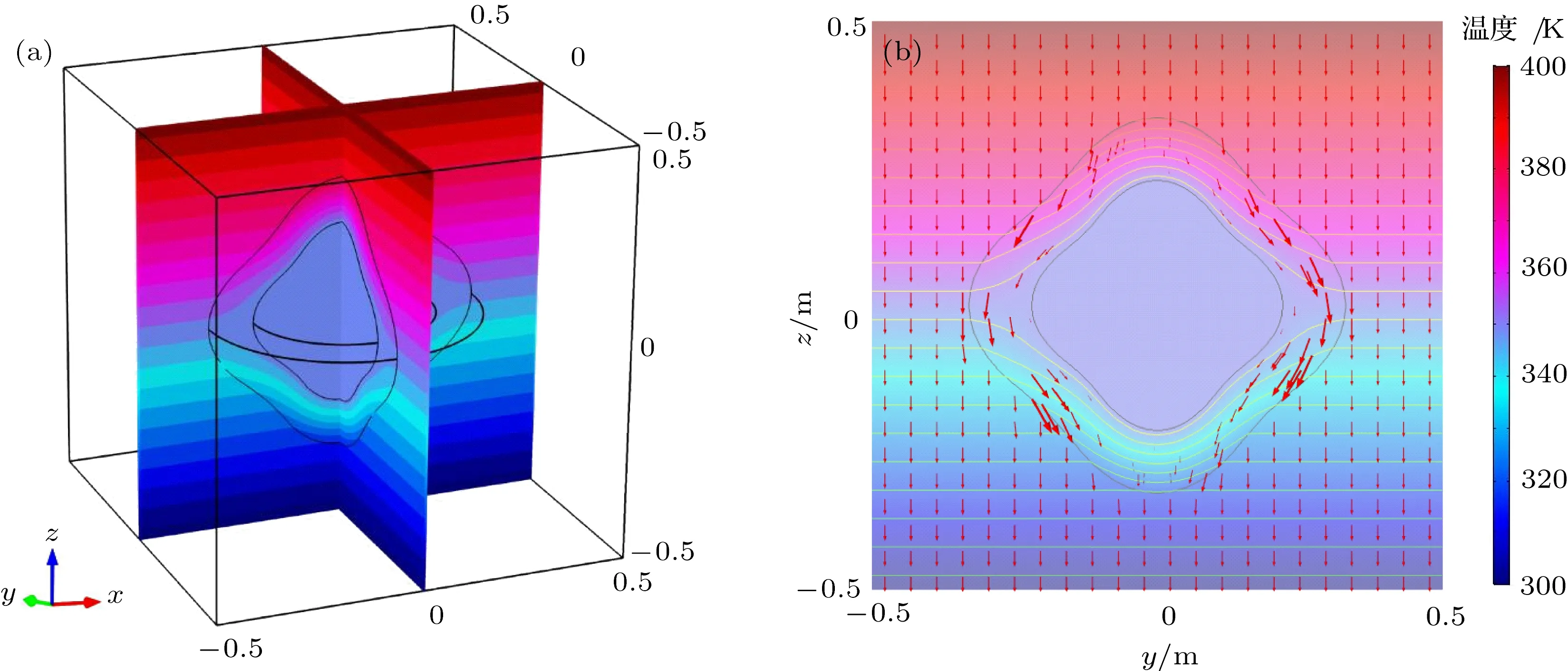
图3 (网刊彩色)共形三维任意形状热斗篷 (a)三维空间温度分布;(b)yoz平面的等温线和热通量分布Fig.3. (color online)Three-dimensional conformal thermal cloak with arbitrary shapes:(a)Threedimensional temperature distribution;(b)isotherms and heatflux profile in the yoz plane.

3.2 非共形热斗篷

为了验证方便,本文首先选取外边界函数为球体,内边界保护区域为椭球体.仿真时,球体半径R2(θ′,φ′)=0.3 m, 椭圆的具体参数a=0.15 m,b=0.1 m,c=0.05 m.具体仿真结果如图4所示.

图4(a)和图4(b)是球加椭球非共形热斗篷的整个三维空间温度分布以及yoz平面的热扩散图.球与椭球是实际工程中常见的几何体,由图可以看出,当热流经过斗篷时发生弯曲,从而绕过了内椭球,在斗篷外恢复原传递方向.因此,该斗篷也同样具有热保护和热隐身双重功能.

图5给出了非共形任意三维形状热斗篷的仿真结果. 当外边界函数R2(θ′,φ′)与内边界函数R1(θ′,φ′)比值不为常数,且内边界所围成的区域全部位于外边界之内时,则此热斗篷为非共形热斗篷.仿真时将内外边界参数设置如下∶

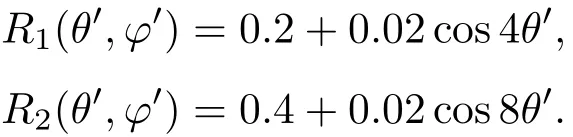
由图5可以看出,内部保护区域没有热流流入,温度保持不变,与外部热流强度大小无关.

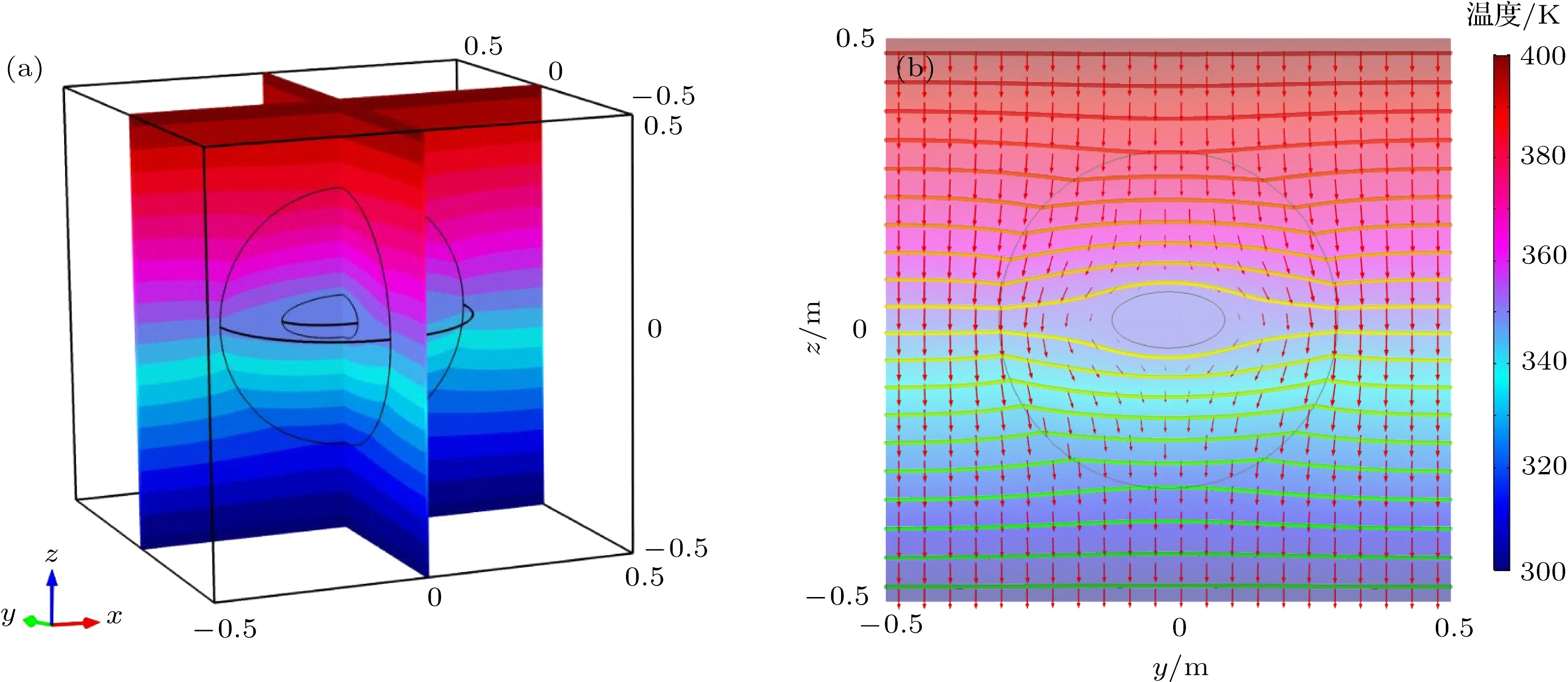
图4 (网刊彩色)球加椭球非共形热斗篷 (a)三维空间温度分布;(b)yoz平面的等温线和热通量分布Fig.4. (color online)Non-conformal thermal cloak with the sphere outside the ellipsoid:(a)Threedimensional temperature distribution;(b)isotherms and heatflux profile in the yoz plane.

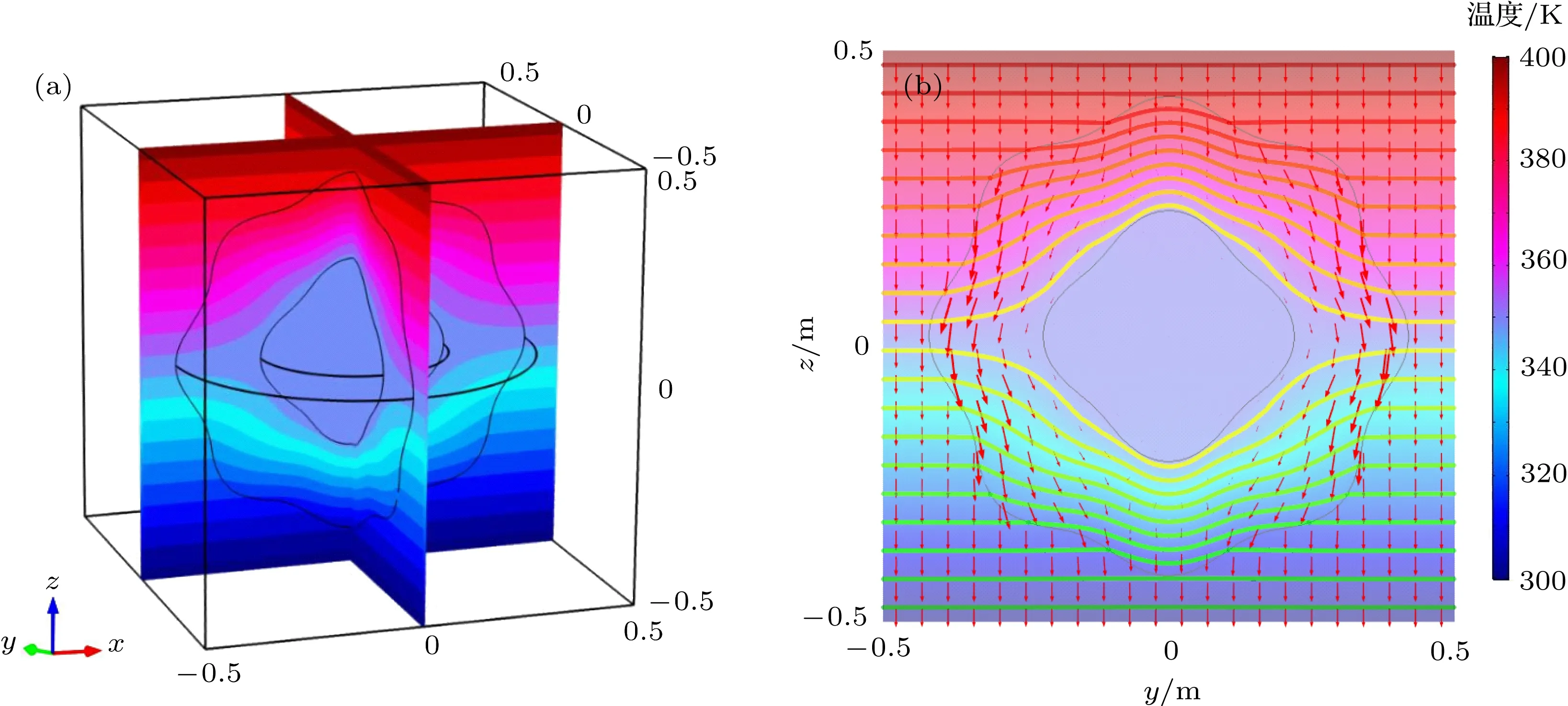
图5 (网刊彩色)非共形三维任意形状热斗篷 (a)三维空间温度分布;(b)yoz平面的等温线和热通量分布Fig.5.(color online)Three-dimensional non-conformal thermal cloak with arbitrary shapes:(a)Threedimensional temperature distribution;(b)isotherms and heatflux profile in the yoz plane.

4 结 论

根据变换热力学的基础理论,推导出了三维任意形状热斗篷的导热系数通用表达式,在此基础上设计了球体、椭球体、共形三维任意形状热斗篷、球加椭球以及非共形三维任意形状热斗篷,并通过有限元软件Comsol Multiphysics进行全波仿真,结果验证了本文所推导的三维任意形状热斗篷导热系数的正确性.在这五个算例中,热流均能在热斗篷的引导下平滑地绕过保护区域,使得保护区域不受外部热流的影响,从而起到了保护作用;同时,在热斗篷之外的区域与原先的温度场一样,并没有被保护区域的目标破坏,保持“隐形”的状态.

相比于先前对二维任意形状热斗篷以及球体、椭球体等规则三维热斗篷的研究,本文将变换热力学应用到了三维任意形状的热斗篷中去,具有更好的普适性,更加贴近工程实际应用,同时也为目标的热隐身和热保护提供了一种有效途径.

[1]Pendry J B,Schurig D,Smith D R 2006 Science 312 1780

[2]Leonhardt U 2006 Science 312 1777

[3]Pendry J B,Schurig D,Smith D R 2006 Opt.Express 14 9794

[4]Pendry J B,Schurig D,Smith D R 2007 Opt.Express 15 14772

[5]Liu Y,Zentgraf T,Bartal G,Zhang X 2010 Nano Lett.10 1991

[6]Schurig D,Mock J J,Justice B J,Cummer S A,Pendry J B,Starr A F,Smith D R 2006 Science 314 977

[7]Cummer S A,Popa B,Schurig D,Smith D R,Pendry J B 2006 Phys. Rev. E 74 036621

[8]Rahm M, Schurig D, Roberts D A, CummerSA,SmithDR,PendryJB2008Photon. Nanostruct. Fundam. Appl.6 87

[9]Aubry A,Lei D Y,Fernándezdomínguez A I,Sonnefraud Y,Maier S A,Pendry J B 2010 Nano Lett.10 2574

[10]Xu H X,Wang G M,Qi M Q,Li L,Cui T J 2013 Adv.Opt.Mater.1 495

[11]Chen H,Chan C T 2007 Appl.Phys.Lett.90 241105

[12]Enoch S,Tayeb G,Sabouroux P,Guérin N,Vincent P 2002 Phys.Rev.Lett.89 213902

[13]Chen Y,Yang F,Xu J Y,Liu X J 2008 Appl.Phys.Lett.92 151913

[14]Wei Q,Chen Y,Liu X J 2012 Appl.Phys.A 109 913

[15]Zhang S,Genov D A,Sun C,Zhang X 2008 Phys.Rev.Lett.100 123002

[16]Farhat M,Guenneau S,Enoch S 2009 Phys.Rev.Lett.103 024301

[17]Hu R,Wei X L,Hu J Y,Luo X B 2014 Sci.Rep.4 3600

[18]Li T H,Zhu D L,MaofC,Huang M,Yang J J,Li S B 2016 Front.Phys.11 1

[19]Fan C Z,Gao Y,Huang J P 2008 Appl.Phys.Lett.92 251907

[20]Guenneau S,Amra C,Veynante D 2012 Opt.Express 20 8207

[21]Schittny R,Kadic M,Guenneau S,Wegener M 2013 Phys.Rev.Lett.110 195901

[22]MaofC,Li T H,Huang M,Yang J J,Chen J C 2014 Acta Phys.Sin.63 014401(in Chinese)[毛春福,李廷华,黄铭,杨晶晶,陈俊昌2014物理学报63 014401]

[23]Qin C L,Yang J J,Huang M 2014 Acta Phys.Sin.63 194402(in Chinese)[秦春雷,杨晶晶,黄铭2014物理学报63 194402]

[24]Yang S M,Tao W Q 2006 Heat Transfer(4th Ed.)(Beijing:Higher Education Press)p43(in Chinese)[杨世铭,陶文铨 2006传热学(第四版)(北京:高等教育出版社)第43页]

[25]Yang T Z,Huang L J,Chen F,Xu W K 2013 J. Phys. D: Appl. Phys.46 305102

[26]Chen T,Weng C N,Tsai Y L 2015 J.Appl.Phys.117 054904

[27]Wu Q,Zhang K,MengfY,Li L W 2010 Acta Phys.Sin.59 6071(in Chinese)[吴群,张狂,孟繁义,李乐伟2010物理学报59 6071]

PACS∶44.10.+I,05.70.—a,81.05.Xj,07.05.TpDOI∶10.7498/aps.66.104401

*Project supported by the National Natural Science Foundation of China(Grant No.11504426)and the National Defense Foundation of China(Grant No.1010502020202).

†Corresponding author.E-mail:yangli123123@126.com

Design and research of three-dimensional thermal cloak with arbitrary shape based on the transformation thermodynamics∗

Xia GeYang Li†Kou WeiDu Yong-Cheng
(College of Power Engineering,Naval University of Engineering,Wuhan 430033,China)

22 November 2016;revised manuscript

9 March 2017)

Based on the form-invariance of the thermal conduction equation different from wave equation,transformation thermodynamics has opened up a new area for the arbitrarily manipulating of heatfluxes at discretion by using thermal metamaterials.Moreover,it can help researchers to design different kinds of thermal devices with many unique properties that cannot be simply realized by natural materials,such as thermal cloaking,thermal concentrating,thermal rotating and thermal illusion.Among these devices,the conventional thermal cloak enabling heatfluxes to travel around the inner region,has attracted the most significant attention so far.At the present time,the studies of the thermal cloak mainly focus on two-dimensional space with arbitrary shape and three-dimensional space with regular shape,which appear to be far from enough to meet the engineering requirements.In this paper,we derive the general expression of the thermal conductivity for three-dimensional thermal cloak with arbitrary shape according to the transformation thermodynamics.In this paper,the thermal conductivity in the polar coordinate system is transformed into that in the Cartesian coordinate system by means of coordinate transformation.On the basis of the expression of the thermal conductivity,we adopt full-wave simulation by using the software COMSOL Multiphysics to analyze the cloaking performances offive designed thermal cloaks,i.e.,spherical thermal cloak,ellipsoidal thermal cloak,three-dimensional conformal thermal cloak with arbitrary shapes,non-conformal thermal cloak with the sphere outside the ellipsoid,and three-dimensional non-conformal thermal cloak with arbitrary shapes.The results show that the heatfluxes travel around the protection area,and eventually return to their original paths.The temperature profile inside the thermal cloak keeps unchanged,and the temperature field outside the thermal cloak is not distorted,which proves that the cloak has a perfect thermal invisible effect.Both the conformal and non-conformal thermal cloak have perfect thermal protection and invisible function.In this paper,the transformation thermodynamics is extended from two-dimensional thermal cloak to three-dimensional thermal cloak with better universality.At the same time,this technology provides morefl exibility in controlling heat flow and target temperature field,which will have potential applications in designing microchip,motor protection and target thermal stealth.It is believed that the method presented here can be applied to other branches of physics,such as acoustics,matter waves and elastic waves.

∶transformation thermodynamics,thermal cloak,three-dimensional arbitrary shape,temperature field

∗国家自然科学基金(批准号:11504426)和国防预研基金(批准号:1010502020202)资助的课题.

†通信作者.E-mail:yangli123123@126.com

©2017中国物理学会Chinese Physical Society