吸附氢分子的振动态及熵的计算∗

王小霞 刘鑫 张琼 陈宏善

(西北师范大学物理与电子工程学院,甘肃省原子分子物理与功能材料重点实验室,兰州 730070)

吸附氢分子的振动态及熵的计算∗

王小霞 刘鑫 张琼 陈宏善†

(西北师范大学物理与电子工程学院,甘肃省原子分子物理与功能材料重点实验室,兰州 730070)

(2016年10月13日收到;2017年3月10日收到修改稿)

用第一性原理方法研究了H2在(MgO)9及(AlN)12团簇上的吸附态、振动模式及熵.分析表明,吸附体系的振动中有六个简正模式可归为氢分子的振动;由于氢分子质量很小,零点能修正对吸附能有重要影响.利用振动配分函数计算了吸附氢分子的熵,表明吸附态H2的熵主要决定于较低的同相振动的频率,并不完全与吸附强度相关;在标准大气压下70—350 K的温度范围内,吸附H2的熵与气态H2的熵之间存在很好的线性关系,吸附后H2的熵减小约10.2R.

∶团簇,H2吸附,振动态,吸附H2的熵

PACS∶36.40.—c,31.15.A—,68.43.BcDOI∶10.7498/aps.66.103601

1 引 言

气体或液体分子在固体表面的吸附涉及广泛的应用领域,在吸附态下分子的平动被限制,而分子具有振动或转动运动.吸附过程的焓变和熵变决定了吸附的平衡状态、吸脱附的动力学、表面反应的反应速率常数等重要物理量,但对吸附态的熵理论计算和实验测量都比较困难[1,2].氢气作为潜在的理想能源,吸附态的熵对于确定最佳的存储条件以及存储材料的选择都十分重要[3,4].Yang等[5]基于van’t Hof f方程分析了吸附熵变对于存储条件的影响,Tang等[6]测量了MSiH3(M=K,Rb,Cs)体系脱附过程的熵变并讨论了熵和焓的补偿作用.氢分子的物理吸附能很好地用朗缪尔模型描述,吸附平衡常数K=exp(∆S0/R−∆H/RT),∆S0为标准大气压下的吸附熵变[7];而对于氢分子物理吸附态的熵,仅有100 K左右H2吸附在分子筛中的实验研究报道[8].在有关讨论固体储氢的文献中,由于对吸附态的熵假定不同,给出的最佳储存条件差别很大.例如Bhatia和Myer[7]假定吸附的熵变为8R,给出室温下储氢的理想吸附能为15.1 kJ/mol;而Li等[9]和Garberoglio等[10]假定不同的熵变并给出了完全不同的理想吸附能.最近Campbell和Sellers[1]测量了多种气体吸附态的熵,但并未包含H2的吸附.本文利用第一性原理方法,研究了H2在(MgO)9及 (AlN)12团簇上的吸附,分析了吸附H2的振动态并计算了吸附态H2的熵.

2 计算方法

氢分子的吸附结构优化及振动频率计算釆用二阶微扰理论(MP2)[11],基函数选取了包括极化函数的三ξ基组6-311 G(d,p)[12];为了得到可靠的振动频率,结构优化采用了verytight的收敛条件(原子上的最大力为0.000002 a.u.,最大位移0.000006 a.u.).计算用Gaussian09程序[13]完成.对吸附体系的振动进行分析,得到吸附H2的配分函数,利用熵与配分函数的关系[14]

计算H2吸附态的熵,式中N为阿伏伽德罗常数,k为玻尔兹曼常数,β=1/(kT).

3 结果与讨论

3.1 吸附态H2的振动模式

氢分子很小不易极化,吸附一般较弱.MgO和AlN都是典型的离子团簇,能够对H2形成较强的吸附[15,16].对于MgO团簇,我们选取了稳定的岩盐和管状(MgO)9[17,18],而对AlN团簇我们选择了笼状的(AlN)12幻数结构[19,20].对H2吸附结构的优化表明,稳定的吸附方式是H2吸附在单个原子上,其中H2在阳离子上以侧位方式吸附,在阴离子上以端位方式吸附.笼状(AlN)12中所有Al或N原子都等价,对于H2在 (MgO)9上的吸附,我们选择了在岩盐结构四配位Mg/O原子(Mg4c,O4c)和管状结构三配位Mg/O原子(Mg3c,O3c)上的吸附.吸附态的熵决定于氢分子的振动频率,而振动频率依赖于吸附强度,因此我们选取具有不同吸附强度的结构以便于考察吸附态的熵与吸附强度的关系.图1给出了六种吸附结构,也给出了各吸附结构的吸附能∶

其中Ecluster,EH2为团簇与自由H2的能量,Ecluster@H2为吸附体系的能量.

对于一个N粒子体系,将其势能在平衡位置做级数展开,引入质量权重的位移坐标qi=则

是正定的实对称矩阵,可用正交矩阵L=[lij]将其对角化.对角化后有Nf(线性分子为3N−5,非线性分子为3N−6)个非负本征值ki,对应的本征矢为

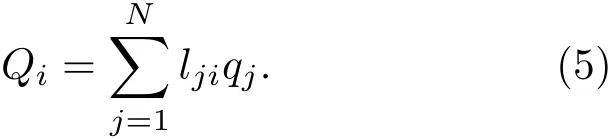
在上述变换下,体系振动的哈密顿量

图1 (网刊彩色)H2在岩盐和管状(MgO)9及笼状(AlN)12上的吸附结构Fig.1.(color online)Structures of H2molecule adsorbed on rocksalt or tube(MgO)9and(AlN)12cages.

分离变量求解则得到一系列独立的简谐振动.在每个振动模式中所有原子都以相同的频率、相位振动,(5)式给出的Qi称为简正坐标.

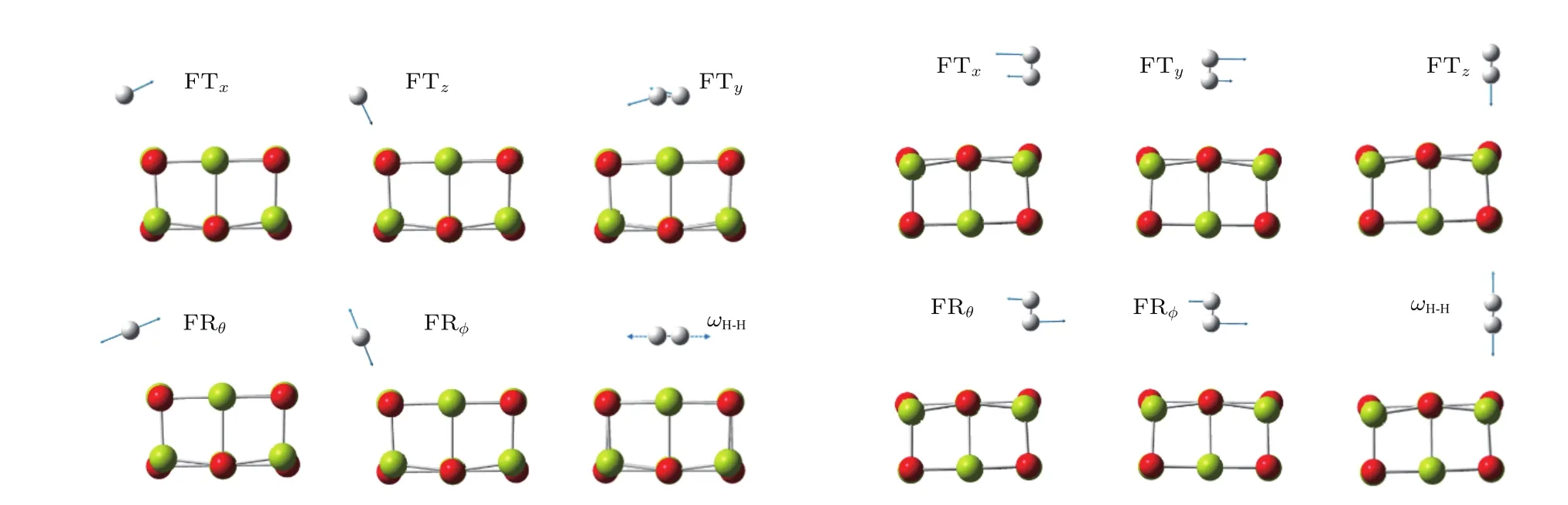
图2 (网刊彩色)H2吸附在岩盐(MgO)9中Mg或O原子上的简正振动模式Fig.2.(color online)Normal vibrational modes of H2adsorbed on Mg or O atoms in rocksalt(MgO)9.

H2吸附在团簇上后,吸附体系比原团簇多出六个振动自由度,通过GaussView对振动模式逐一甄别,发现有六个简正振动可归为氢分子,图2为H2吸附在岩盐 (MgO)9上的简正振动模式.对图1各吸附结构中H2的简正振动模式对应的简正坐标进行仔细核查,发现团簇原子的振幅比氢分子的振幅一般小两个数量级.在H2的六个振动模式中,沿着H2到吸附位方向的同相振动用FTz表示,与之垂直的同相振动中,频率较低的用FTx表示、频率较高的用FTy表示;H2以端位方式吸附在阴离子上时,与FTz相对应的异相振动即为H2内的伸缩振动ωH-H,而以侧位方式吸附在阳离子上时,ωH-H与FTy对应;另外两个异相振动相当于H2的转动,分别用FRθ和FRϕ表示.

表1列出了图1各吸附态H2的振动频率.除Al原子上的FTy外,其他FTx与FTy的振动频率都在100 cm−1以下,表明势能面的底部较平.FTz的振动频率和吸附强度相关,H2吸附在阳离子上时FTz约为300 cm−1,在阴离子上时为100 cm−1多.H2吸附在阳离上时FRθ和FRϕ对应的频率差别较大,而在阴离子上时两个频率比较接近.用相同算法得到的自由氢分子的振动频率ωH-H为4533.23 cm−1,由于吸附后H2内的结合减弱,从表1中可看出ωH-H约降低100 cm−1.

表1 吸附态H2的振动频率(单位为cm−1)Table 1.Vibration frequencies of absorbed H2(units:cm−1).

3.2 零点能对H2吸附能的影响

(4)式给出的力常数与折合质量成反比,对应的振动频率与质量的平方根成反比;对于H2的六个简正模式,折合质量近似为H2的质量,所以其振动频率较高,零点能修正对吸附能有较大的影响.因频率计算比较费时,在许多研究储氢的文献中并没有考虑零点能的修正[21−26].表2列出了(2)式定义的吸附能∆E、零点能修正∆ZPE以及考虑零点能修正以后的吸附能Eb.对于零点能修正表2中列出了用两种方法计算的值,第一种是

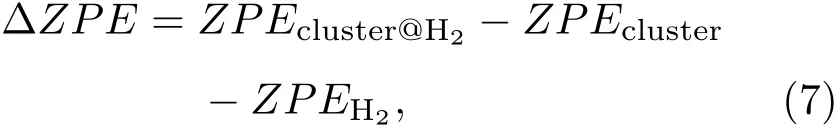
其中ZPEcluster,ZPEH2为团簇与自由H2的零点能,ZPEcluster@H2为吸附体系的零点能.第二种是利用表1的频率直接求得,鉴于吸附后H2内的振动频率明显降低,考虑了伸缩振动频率的变化ħ∆ωH-H/2∶

从表2可以看出两种方法计算的零点能非常一致,再次验证了我们甄选氢分子简正模式的正确性.表2数据表明,在阳离子Mg3c,Al和Mg4c上零点能修正达到了∆E的64%,88%和97%,因此修正后吸附能大幅减小;而在阴离子上零点能修正都已超过了∆E,因此在阴离子上的吸附不稳定.

表2 H2吸附能及零点能修正(单位为eV)Table 2.Adsorption energy and zero-point energy correction of H2(units:eV).

3.3 氢分子吸附态的熵

在简谐近似下,N粒子体系的振动近似为Nf=3N−6个独立的简谐振动的迭加,其振动配分函数为

其中θvj=ħωj/k为振动特征温度.由(1)式得到振动熵

它们为各简正模式的熵的和.由于H2的振动和其他简正模式独立,根据表1中的振动频率便可得到吸附态H2的熵值Sads.

Gaussian程序在进行频率计算时直接给出了体系在标准状态下的振动熵值,由于气态H2的振动频率很高,常温下处在振动基态对熵无贡献,将吸附体系与团簇的振动熵值相减

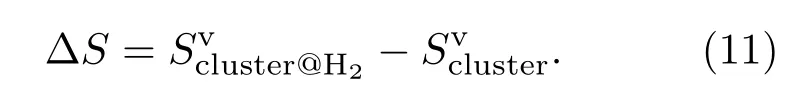
也给出H2吸附态的熵.表3给出了利用(10)式计算的标准态下H2吸附态的熵Sads与∆S,两者也非常一致.

表3 T=298.15 K时吸附态H2的熵(单位为J/mol·K)Table 3.The entropy of adsorbed H2at T=298.15 K(units:J/mol·K).

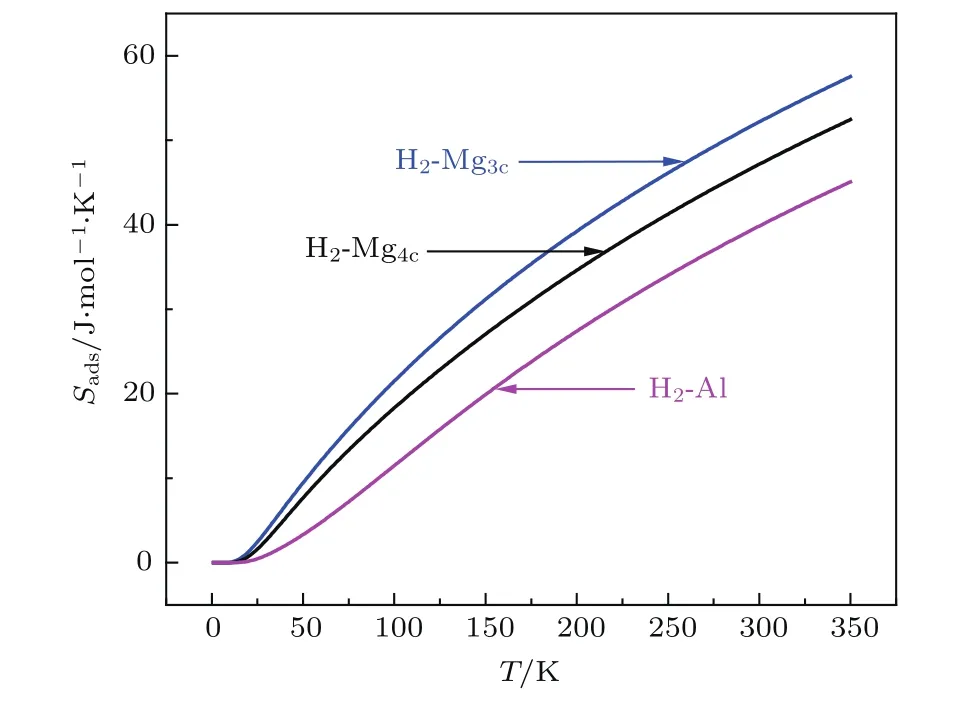
图3 (网刊彩色)不同温度下吸附H2的熵值Fig.3.(color online)The entropy of adsorbed H2at different temperature.

图3为不同温度下吸附态H2的熵,温度较低时熵值增加较快,超过150 K时Sads随温度近似做线性变化.(10)式表明振动熵对低频比较敏感,H2吸附态的熵值主要由两个同相的振动频率FTx和FTy决定;FTz与吸附强度相关,而FTx和FTy主要由势能面底部形状决定,因此吸附态的熵并不完全与吸附强度相关.如在Mg3c上的吸附最强,但在Al上吸附的熵值最小.

为了研究H2吸附前后的熵变,我们进一步考察了H2吸附态的熵和气态熵Sgas的关系.气态H2的振动对熵无贡献,平动的熵容易由下式算出∶

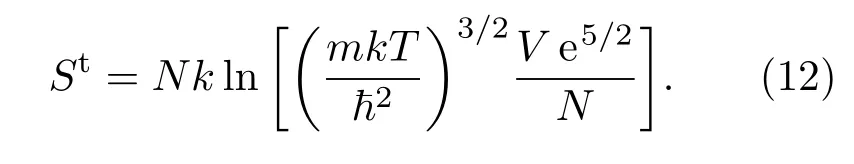
双原子分子的转动配分函数为

其中θr=ħ2/(2Ik)(I为转动惯量).由于H2是同核双原子分子,仲氢(核自旋波函数为交换反对称的单重态)只能处在l为偶数的转动能级上,而正氢(核自旋波函数为交换对称的三重态)只能处在l为奇数的转动能级上.利用熵与配分函数的关系可得到仲氢和正氢的转动熵

计算分别取了前四项,当温度低于350 K时上述两式能保证计算的精度高于10−6.由于自旋禁阻效应,常温下制备的H2当温度降低时仲氢和正氢并不相互转变而保持1∶3的比例,对仲氢和正氢的熵加权平均可得到气态H2的转动熵S(R).图4为仲氢、正氢、气态H2的转动熵以及气态H2的总熵S(T+R)(平动+转动)随温度的变化,当T高于150 K时转动熵及总的熵都随温度近似做线性变化.

图4 (网刊彩色)气态H2的转动熵及总的熵值Fig.4.(color online)Rotational and total entropy of gas-phase H2.

图5给出了标准大气压下温度从70 K到350 K时吸附态与气态H2熵的关系,可以看出二者具有较好的线性关系,对数据做线性拟合

对于H2在Mg3c,Mg4c和Al上的吸附,a分别为0.98,1.05和0.95;S0分别为−81.6,−85.58和−85.95.即斜率接近1,而吸附后H2的熵减小约10.2R.因为H2的质量小,平动、转动及振动熵与温度的关系与较重的分子都有明显的差别,因此拟合结果相较Campbell给出的斜率0.7和截距−3.3R不同[1].但这一结果却偶然地与特鲁顿规则非常接近,即在沸点(饱和蒸气压为1 bar)时非极性液体的吸附熵与气相熵近似为线性关系,斜率为1时截距为−10.3R.

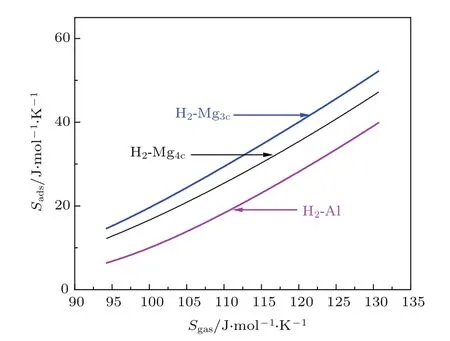
图5 (网刊彩色)P=1 bar,T=70—350 K时吸附态H2与气态H2熵的关系Fig.5.(color online)The correlation between entropy of adsorbed H2and entropy of gas-phase at P=1 bar,T=70–350 K.

4 结 论

选取了H2在岩盐和管状(MgO)9及笼状(AlN)12上的吸附,计算了振动频率,分析了吸附H2的振动,计算了吸附的熵变.对吸附体系振动模式的分析表明,氢分子的振动可以从其他简正模式中独立出来,属于H2的六个简正模式中团簇原子的振幅小两个数量级.由于振动频率与质量的平方根成反比,对氢分子的吸附,零点能修正超过了吸附能的一半,修正后阴离子上的吸附能为正.鉴于氢分子的振动与其他简正模式独立,可以利用氢分子的振动频率计算吸附H2的熵,因较低的两个同相振动频率主要由势能面底部形状决定,吸附态的熵并不完全与吸附强度相关.在标准大气压下温度从70 K到350 K变化时,H2吸附态的熵与气态熵之间存在很好的线性相关,吸附后H2的熵减小约10.2R.

感谢国家超级计算机中心在广州和深圳提供的计算资源.

[1]Campbell C T,Sellers J R 2012 J.Amer.Chem.Soc.134 18109

[2]de Moor B A,Ghysels A,Reyniers M F,van S V,Waroquier M,Marin G B 2011 J.Chem.Theory Comput.7 1090

[3]Simon C M,Kim J,Lin L C,Martin R L,Haranczyk M,Smit B 2014 Phys.Chem.Chem.Phys.16 5499

[4]Efremenko I,Sheintuch M 2005 Langmuir 21 6282

[5]Yang J,Sudik A,Wolverton C,Siegel D J 2010 Chem.Soc.Rev.39 656

[6]Tang W S,Chotard J N,Raybaud P,Janot R 2014 J.Phys.Chem.C 118 3409

[7]Bhatia S K,Myers A L 2006 Langmuir 22 1688

[8]Otero Areán C,Nachtigallová D,Nachtigall P,Garrone E,Rodríguez Delgado M 2007 Phys.Chem.Chem.Phys.9 1421

[9]Li J,Furuta T,Goto H,Ohashi T,Fujiwara Y,Yip S 2003 J.Chem.Phys.119 2376

[10]Garberoglio G,Skoulidas A I,Jognson J K 2005 J.Phys.Chem.B 109 13094

[11]Møller C,Plesset M S 1934 Phys.Rev.46 618

[12]Hehre W J,Pople J A 1972 J.Chem.Phys.56 4233

[13]Frisch M J,Tracks G W,Schlegel H B,et al.2013 Gaussian09 Revision D.01 Wallingford CT:Gaussian,Inc.

[14]Wang Z C 2008 Thermodynamics and Statistical Physics(Beijing:Higher Education Press)p192(in Chinese)[汪志成2008热力学统计物理(北京:高等教育出版社)第192页]

[15]Larese J Z,Arnold T,Frazier L,Hinde R J,Ramirez-Cuesta A J 2008 Phys.Rev.Lett.101 165302

[16]Wang Q,Sun Q,Jena P,Kawazoe Y 2009 ACS Nano 3 621

[17]Zhang Y,Chen H S,Yin Y H,Song Y 2014 J.Phys.B 47 025102

[18]Dong R,Chen X S,Wang X F,Lu W 2008 J.Chem.Phys.129 044705

[19]Liu Z F,Wang X Q,Liu G B,Zhou P,Sui J,Wang X F,Zhu H J,Hou Z 2013 Phys.Chem.Chem.Phys.15 8186

[20]Yong Y L,Song B,He P 2011 Phys.Chem.Chem.Phys.13 16182

[21]Okamoto Y,Miyamoto Y 2001 J.Phys.Chem.B 105 3470

[22]Sun Q,Wang Q,Jena P,Kawazoe Y 2005 J.Amer.Chem.Soc.127 14582

[23]Yildirim T,Ciraci S 2005 Phys.Rev.Lett.94 175501

[24]Zhao Y,Kim Y H,Dillon A C,Heben M J,Zhang S B 2005 Phys.Rev.Lett.94 155504

[25]Sun Q,Jena P,Wang Q,Marquez M 2006 J.Amer.Chem.Soc.128 9741

[26]Yoon M,Yang S,Hicke C,Wang E,Geohegan D,Zhang Z 2008 Phys.Rev.Lett.100 206806

PACS∶36.40.—c,31.15.A—,68.43.BcDOI∶10.7498/aps.66.103601

*Project supported by the National Natural Science Foundation of China(Grant Nos.11164024,11164034).

†Corresponding author.E-mail:chenhs@nwnu.edu.cn

Vibration states and entropy of adsorbed hydrogen molecules∗

Wang Xiao-Xia Liu Xin Zhang Qiong Chen Hong-Shan†
(College of Physics and Electronic Engineering,Northwest Normal University,Key Laboratory of Atomic and Molecular Physics and Functional Materials of Gansu Province,Lanzhou 730070,China)

13 October 2016;revised manuscript

10 March 2017)

The entropy and enthalpy changes upon absorption determine the equilibrium adsorption states,the adsorption/desorption kinetics,and the surface reaction rates.However,it is difficult to measure experimentally or calculate theoretically the entropy of adsorption state.Hydrogen is considered as the most promising candidate to solve the global energy problems,and the storage by adsorption on light porous solids constitutes a main avenue to research field.An ideal storage system should be able to operate under ambient conditions with high recycling capacity and suitable uptake-release kinetics.The entropy of adsorbed H2molecules is of great significance for determining the optimum conditions for hydrogen storage and for designing the storage materials.To the best of our knowledge,however,the only report on the entropy of the adsorbed H2molecules is that adsorbed on alkali-metal exchanged zeolites at temperatures around 100 K.Due to different assumptions of the entropy changes,the values of the optimum enthalpy∆H reported in the publications cover a wide range.In this paper,the adsorption states,vibrational modes,and the entropies of H2molecules adsorbed on(MgO)9and(AlN)12clusters are studied by usingfirst principal method.The computation is performed by the second-order perturbation theory(MP2)with the triple zeta basis set including polarization functions 6-311G(d,p).The very-tight convergence criterion is used to obtain reliable vibration frequencies.Analysis shows that six vibrational modes of the adsorption complexes can be attributed to the vibration of H2molecule.For these normal modes,the amplitudes of the displacements of cluster atoms are usually two orders smaller than those of the hydrogen atoms.As the vibrational frequency is inversely proportional to the square root of the mass,the zero-point energy has an important influence on the adsorption energy.The ZPE correction exceeds half of the adsorption energy,and the adsorption on the anions is not stable after including the correction.Under the harmonic approximation,the normal vibration modes are independent,so the entropy of adsorbed H2molecules can be calculated by using the vibrational partition function based on the vibrational frequencies.The results indicate that the entropy values depend mainly on the two lowest in-phase vibrational frequencies and it is not directly related to the adsorption strength but determined by the shape of the potential energy surface.In a temperature range of 70–350 K and at a pressure of 0.1 MPa,there is a good linear correlation between the entropy of adsorbed H2and the entropy of gas-phase.The entropy of H2decreases about 10.2R after adsorption.

∶cluster,H2adsorption,vibration states,entropy of adsorbed H2

∗国家自然科学基金(批准号:11164024,11164034)资助的课题.

†通信作者.E-mail:chenhs@nwnu.edu.cn

©2017中国物理学会Chinese Physical Society