任务呈现方式、任务呈现顺序影响青少年算术策略运用的年龄差异

孙 玉 卢 淳 司继伟 王婷婷

（山东师范大学心理学院，济南 250358）

任务呈现方式、任务呈现顺序影响青少年算术策略运用的年龄差异

孙 玉 卢 淳 司继伟 王婷婷

（山东师范大学心理学院，济南 250358）

结合选择／无选法与改进的PRP双任务范式，通过设置不同任务呈现顺序（字母先呈现、算术先呈现）、任务呈现方式（随机组、固定组）考察双任务协调时青少年算术策略运用的年龄特征。127名不同年级青少年参加了本实验。结果表明：（1）任务呈现方式影响双任务情境下的算术策略运用，随机组的算术策略运用表现显著差于固定组；（2）任务呈现顺序影响双任务情境下的算术策略运用，字母先呈现时的算术策略运用表现显著差于算术先呈现；（3）随着年级升高，青少年在双任务情境下的算术策略运用能力逐步提高，这种发展变化的速度是不同的。

算术策略运用；双任务协调；年龄差异；青少年

1 引言

算术能力在个体的学习、工作及日常生活中起着至关重要的作用。近年来许多研究发现，个体的算术表现与策略运用存在密切联系［1］。策略运用是指在任务情景中，个体在问题空间中选择不同策略并进行有效执行的操作加工过程，主要包含策略的选择以及执行［2］。大量实证研究发现算术策略的运用受到多种因素的影响，如情境因素［3］、个体特征［2，4］、策略特征［5-8］、问题特征［9-11］等。

近年来研究者发现中央执行系统在个体的算术策略运用中可能扮演着重要角色。司继伟、杨佳、贾国敬、周超考察了不同中央执行负荷对估算策略运用的影响，结果发现在无负荷条件下个体策略适应性更好［12］。Imbo与Vandierendonck对中央执行进行了干扰，结果发现心算任务成绩和策略选择的适宜性都受到干扰［13］。进一步研究发现，在选择估算策略方面，中国被试比西方被试更容易受到中央执行负荷的影响［14，15］。Collette和Linden采用神经成像的方法将执行功能分解为四种基本成分：抑制（inhibition）、转换过程（shifting process）、刷新（updating）以及双任务协调（dual-task coordination）［16］。因此，作为中央执行重要功能之一的双任务协调可能会在一定程度上对算术策略运用产生影响。双任务协调是一种独立存在的中央执行功能，指的是大脑如何将认知资源分配到两个或多个同时进行的加工任务。双任务协调能力独立于特定的任务，并可以部分迁移到其他的双任务情境中［17］。

目前关于算术认知策略的研究多在单任务情境下进行，涉及双任务的研究相对较少。事实上，在日常生活中的很多时候，我们要同时从事多种任务，需要将注意分配到两个或两个以上的并发任务上，比如：过马路时打电话，开车时调广播频道，看电视节目时做饭等等。个体在同时完成多种任务时需要双任务协调的参与，因此，双任务协调不仅是中央执行的重要功能，也是个体的重要认知能力，对其进行研究具有重要的意义。相对单任务，在双任务情境下，个体的反应时更长，错误率更高［18，19］。陈英和与王明怡发现双任务协调与策略放弃次数的增加呈负相关，并指出作为中央执行系统的重要成分之一，双任务协调可能也会参与到个体策略运用上来［20］。杨佳、李颖慧、司继伟和张明亮也发现，与单纯估算任务情境下的表现相比，双任务下的估算表现受到了影响，成绩更差［21］。因此，作为中央执行重要功能之一的双任务协调可能会在一定程度上对算术策略运用产生影响。但基于有限研究，目前尚不清楚，个体在不同双任务情境中算术认知策略运用表现是怎样的，又有哪些因素会影响双任务表现。Töllner，Strobach，Schubert和Müller采用同时让被试进行音调高低的辨别和视觉任务水平垂直的定位双任务，来研究任务序列的可预测性与否及其刺激间隔如何影响双任务，结果发现序列顺序的相同与否会影响双任务协调［3］。Szameitat等采用fMRI技术，让15名被试选择两个反应任务：视觉（右手按键反应）、听觉（左手按键反应），发现不同任务顺序相比于相同任务顺序需要更高的任务协调力［18］。Szameitat，Schubert，Muller和Cramon采用PRP范式并结合fMRI技术，通过设计随机组和固定组探究了哪个组的被试其双任务表现所激活的脑区更大，他们发现个体在不知道任务出现顺序的情况下，激活的脑区更大，这说明个体在知道任务出现顺序的情况下的表现要好于个体在不知道的情形下的表现［22］。因为个体在不知道任务呈现顺序的情况下，在前后两个不同任务之间的转换就需要额外的努力，这就导致了更大的脑区激活。那么，任务呈现方式是否影响双任务协调时个体的算术策略运用情况？如果存在影响，那么不同的任务呈现顺序又会产生怎样的影响？本研究将通过设置不同的任务呈现方式和任务呈现顺序，探讨不同双任务情境在双任务协调对个体算术策略运用影响中的作用。所谓任务呈现顺序，是指两个任务哪个先呈现，哪个后呈现。任务呈现方式则指，若将两个任务（双任务）作为一个试次，那么各个试次是如何呈现的，是随机呈现（两任务随机呈现）还是固定呈现（两任务按固定顺序呈现）。

此外，个体的双任务表现存在年龄差异，诸多研究也考察了双任务协调的年龄差异［23，24］。然而这些研究涉及的年龄跨度比较大，他们仅仅关注的是不同年龄的群体在双任务情境下的表现存在什么样的差异，但不利于考察个体在双任务表现的发展趋势问题。杨佳通过双任务范式研究发现，在中央执行有负荷的情况下，六年级儿童与四年级儿童策略表现的差异远远小于六年级儿童与成人之间的差异［25］。据此推测，在六年级到成人间的某个阶段，个体在双任务协调情境下的算术策略运用会存在不同的变化。所以，为了便于对此问题进行考察，本研究选取了六年级、初二和高一三个年级对不同年级阶段青少年的双任务情境下的算术策略运用表现进行了考察，旨在了解青少年双任务协调时算术策略运用的发展变化趋势及特点。

估算是指未经过精确计算而只借助原有知识对问题提出粗略答案［26］。个体进行估算时常用策略包括上调策略（向上取整，如36×47=40×50=2000）和下调策略（向下取整，如36×47=30×40=1200）［2，8，27］。选择／无选法范式常用于算术估算策略的研究［6，8，28］。该范式包含两个实验条件，选择条件和无选条件。选择条件下，个体根据要求选择合适的策略（上调策略／下调策略），用于考察个体的策略选择；无选条件下，个体要使用指定的策略解决问题，用于考察个体的策略执行。PRP范式是双任务操作研究的一个经典范式，也叫心理不应期（psychological refractory period）范式。在这种范式中，要求被试快速、连续地完成两种任务，呈现给被试的两种任务S1和S2用一定的SOA分开，两种任务都需要快速选择反应（R1和R2）。研究者发现PRP范式可以用来考察个体的双任务协调能力［29］。鉴于本研究所考察的对象包括部分小学儿童，考虑到时间因素，对儿童被试需要采用团体施测，因此声音任务不是最佳选择（采用声音任务所涉及的口头报告不能用于团体施测）。因此，将两个任务设置成视觉任务：字母任务和算术任务。

基于以上综述，本研究拟以估算任务为切入点，结合选择／无选法与改进的PRP双任务范式，探究在不同任务呈现方式（随机组、固定组）和任务呈现顺序（字母先呈现、算术先呈现）的双任务协调情境中，不同年龄个体策略运用的情况。相比随机组，在固定组中，个体可以很快选择出适应性策略，将更多的认知资源用于策略执行，从而使得策略运用表现更好。因此，本研究假设，固定组比随机组的表现好。另外，随着年龄增长，个体的工作记忆能力不断提高，而工作记忆又会促进算术策略的选择与执行［30］。因此，本研究假设，年龄大的个体比年龄小的表现好。考察双任务协调情境下个体算术策略运用表现及其年龄发展趋势，有助于进一步揭示策略运用的心理加工机制，深入了解执行功能影响个体算术认知策略的具体机制，对于丰富和完善中央执行和认知策略的理论体系具有重要意义。

2 研究方法

2.1 被试

从江苏省新沂市某小学、初中和高中分别随机选取被试六年级42名、初二41名、高一44名。三组被试的平均年龄分别为12.86岁、14.25岁、16.39岁。将每个年级的被试均随机分成两组，每组被试接受一种任务呈现方式。不同任务呈现方式下被试的分配情况见表1。

2.2 研究设计

采用2（任务呈现顺序：字母先呈现、算术先呈现）×2（任务呈现方式：随机组、固定组）×3（年级：六年级、初二、高一）×3（策略运用条件：最佳选、无选上、无选下）的混合实验设计。其中，任务呈现顺序及策略运用条件为被试内变量，任务呈现方式和年级为被试间变量。因变量为被试完成任务的正确率和反应时。

表1 不同任务呈现方式中各年级组被试的分配情况（人数）

2.3 实验任务与材料

2.3.1 算术技能测验

采用国际通用的数学技能测验 The French Kit［31］。测验包含两个子测验，一个是三个数的加法（如，6+23+44）测验，另一个是减法问题（如，54-12）和乘法问题（如，49×2）的混合测验，每部分又包含两个小部分，共计四个小部分，每一小部分为60道题目，每一部分要求被试在2分钟内解决尽可能多的题目。主试需严格控制时间，时间到即立刻提示被试开始进行下一部分的测试。正确解决的题目总数即为算术技能得分。

2.3.2 字母任务

实验中的双任务之一为字母回忆任务［32］。任务要求被试按顺序回忆字母。所采用的实验材料为由随机选取的四个小写英文字母组成的没有任何意义的字母串，如acqb，共96组（三种实验条件，每种条件下32组）。由于在算术任务中有四个数字，为保证在改变任务呈现顺序的情况下，两个任务的编码数量一致，所以字母任务采用长度为4的字母串。实验中四个字母同时呈现。在字母选取过程中控制了以下因素：（1）字母串中没有相同的字母；（2）四个字母也不能组成英语单词；（3）四个字母不交换顺序重新组合。

2.3.3 算术任务

32道两位数乘法估算题。估算题含16道同质性问题（两个乘数的个位数同时大于或小于5）和16道异质性问题（一个乘数的个位数大于5，一个乘数的个位数小于5）。在16道异质性问题中，包括8道上调题 （用上调策略得到的估算答案与精确计算的答案最接近）和8道下调题（下调策略的结果更接近正确答案）。为了排除算术领域特定效应的影响，根据以往研究［4］，在乘法题目选取上考虑了以下因素［32］：（1）两个乘数的个位数都不能为0或5；（2）两个乘数内都没有重复的数字（如33×67或37×66等不能使用）；（3）两个乘数的十位和个位不能相同（如73×76或37×67等不能使用）；（4）相同问题不交换顺序后使用（如使用37×46，就不再用46×37）。

2.4 实验程序

实验程序通过E-prime1.0软件进行编写。在实验开始前，被试先完成算术技能测验，之后给被试讲解两种估算策略：上调策略和下调策略，被试完全明白如何使用两种策略后进行实验。实验包括两个任务：字母任务和算术任务。字母任务要求被试按照顺序回忆所呈现的字母串，而算术任务在不同的策略运用条件下反应要求有所不同。实验程序分为三个组块：最佳选择、无选上调和无选下调。在每个组块开始前的指导语中告诉被试策略使用的提示，每个组块都包含32道估算题。所有被试均按照最佳选择—无选上调—无选下调的顺序进行实验。

此外，本研究设置两个实验组：随机组和固定组。在随机组中，告知被试两个任务随机出现；在固定组中，前一半的试次先呈现字母任务，后一半试次先呈现估算任务。在任务呈现前先给予被试一个提示，提示任务的呈现顺序。随机组和固定组（以最佳选择条件为例）的流程图分别见图1和图2。

图1 随机组实验流程图

图2 固定组实验流程图

正式实验前，每种实验条件下都预先安排有8道练习题。两个任务都呈现后，就可以分别对两个任务做出反应，反应顺序自由确定。字母任务要求用键盘按顺序输入相应的字母后按Enter键；估算任务要求直接输入结果后按Enter键。

2.5 数据处理

使用SPSS16.0和Excel 2003进行统计分析。

3 实验结果

4名被试没有按要求作答，最后有效被试123人。由于本研究将不同任务呈现方式（随机组、固定组）和任务呈现顺序（字母先呈现、算术先呈现）结合起来研究，而在随机组中由于字母任务和算术任务随机呈现，因此，为考察任务呈现顺序的影响，将所有试次中字母先呈现的试次与算术先呈现的试次分开进行数据分析。

3.1 双任务协调的结果

在双任务协调情境中，个体所面临的两个任务是同等重要的［3］。鉴于此，本实验通过在不同实验条件下，两个任务都正确的比例来考察被试的双任务协调能力。不同年级被试在不同任务呈现方式下的平均数和标准差见表2。

表2 不同任务呈现方式下两个任务都正确的平均比例（M±SD）

在控制算术技能的情况下，对两个任务都正确的平均比率进行2（任务呈现方式：随机组、固定组）×3（年级：六年级、初二、高一）的两因素方差分析，结果发现：任务呈现方式主效应显著，F（1，116）= 8.84，p＜0.01，ηp2=0.07，随机组中，被试两个任务都正确的比例显著低于固定组。年级主效应显著，F（2，116）=5.87，p＜0.01，ηp2=0.09，Bonferroni事后检验表明，高一显著高于六年级（0.64 vs 0.54），高一显著高于初二（0.64 vs 0.57）、六年级与初二差异不显著。二者的交互作用不显著F（2，116）=0.32，p=0.73，ηp2=0.01。总体来说，两种不同的实验情境会产生不同的双任务协调表现，而且随着年龄的增长，表现越好。

3.2 策略选择

策略选择是通过选择条件来实现的，因此在最佳选择条件下分析个体策略选择的正确率和反应时，描述性统计结果见表3和表4。

稻虾共作模式是近几年在湖北及周边省份快速发展起来的一种稻田高效生态种养模式，该模式充分利用稻田水面、土壤和生物资源，发挥了不同物种间资源互补的循环生态效应［1］，实现一水多用、种植养殖结合［2］，既促进稻田增产增效，又净化稻田养殖水体，提高了农产品品质。但在实际生产中，生产者为了追求养殖效益，过量地投喂养殖饲料，未被小龙虾取食的部分便分解残留于养殖水体中，同时小龙虾排放的粪便中亦含有一定量的氮磷营养元素排放到养殖水体中［3］，导致稻田养殖水体中氨氮、亚硝酸盐及磷含量都高于单作水稻田［4］，虽有利于水稻生长，但同时也增加了养殖水体富营养化风险。

前人研究结果显示个体的算术技能会影响策略运用［7，33，34］，因此将其作为协变量加以控制。

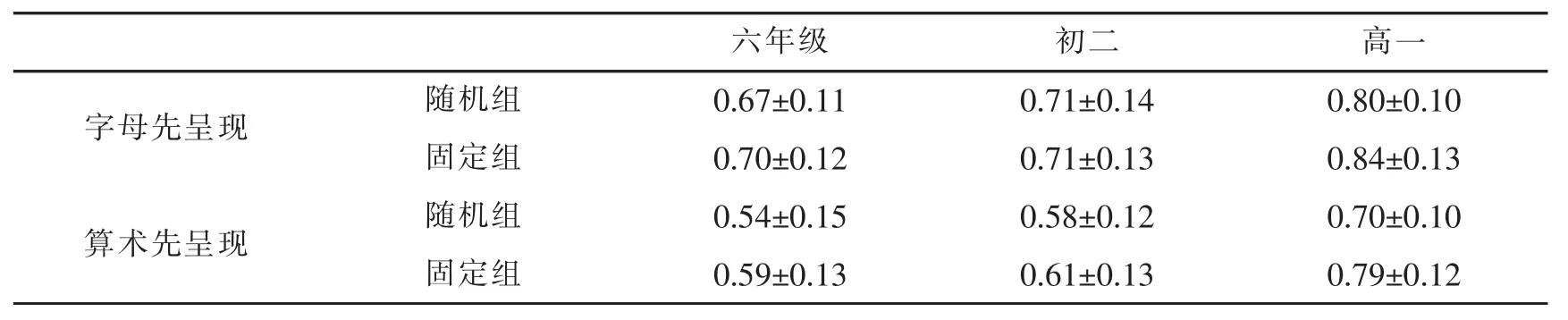
表3 不同年级被试的策略选择正确率（M±SD）

表4 不同年级被试的策略选择反应时（M±SD，单位：ms）

首先，计算了策略选择的反应时和正确率间的相关，r=-0.09，p=0.31，说明不存在速度—准确性权衡。

其次，以算术技能为协变量，对策略选择的正确率进行2（任务呈现顺序：字母先呈现、算术先呈现）×2（任务呈现方式：随机组、固定组）×3（年级：六年级、初二、高一）的重复测量方差分析。结果显示：算术技能主效应显著，F（1，116）=4.87，p＜0.05，ηp2=0.04。年级主效应显著，F（2，116）=24.07，p＜0.001，ηp2=0.29，Bonferroni事后检验发现，六年级显著低于高一 （0.66 vs.0.77），初二显著低于高一（0.63 vs.0.77），六年级与初二无显著差异。任务呈现顺序与任务呈现方式交互作用显著，F（1，116）= 4.70，p＜0.05，ηp2=0.04，简单效应分析发现，在算术先呈现的实验条件下，固定组的策略选择正确率显著大于随机组，F（1，121）=5.04，p＜0.05；在字母先呈现的实验条件下，两组策略选择的正确率没有差异。其余主效应与交互作用均不显著。

最后，以算术技能为协变量，对策略选择的反应时进行2（任务呈现顺序：字母先呈现、算术先呈现）×2（任务呈现方式：随机组、固定组）×3（年级：六年级、初二、高一）的重复测量方差分析。结果显示：年级主效应显著，F（2，116）=5.14，p＜0.01，ηp2=0.08，Bonferroni事后检验发现，六年级显著高于高一（7373 vs.6413ms）、初二显著高于高一 （7126 vs. 6413ms），六年级与初二差异不显著。任务呈现方式主效应显著，F（1，116）=6.60，p＜0.05，ηp2=0.05，随机组的反应时显著大于固定组。任务呈现顺序、年级与任务呈现方式的交互作用显著，F（2，116）=4.26，p＜0.05，ηp2=0.07，（见图3）。简单简单效应分析发现，在随机组中，六年级个体在不同任务呈现顺序题目上的反应时没有显著差异，初二（F（1，117）=8.00，p＜0.05）和高一（F（1，117）=5.06，p＜0.05）算术先出现题目的反应时显著更长；在固定组中，三个年级均无显著差异。其余主效应与交互作用均不显著。

3.3 策略执行

本研究包含无选上调和无选下调两种执行条件，无选上调反映的是被试执行上调策略的情况，无选下调反映的则是下调策略的执行情况。各年级被试策略执行的正确率和反应时见表5和表6。

首先，计算了执行上调策略的反应时和正确率间的相关，r=0.11，p=0.249，又计算了执行下调策略的反应时和正确率间的相关，r=-0.04，p=0.961，说明均不存在速度—准确性权衡。

在正确率上，年级主效应显著，F（2，116）=3.25，p＜0.05，ηp2=0.05，Bonferroni事后检验表明，六年级和高一被试策略执行的正确率差异边缘显著（0.95vs.0.97），六年级与初二、初二与高一被试的差异不显著。任务呈现顺序主效应显著，F（1，116）=8.45，p＜0.01，ηp2=0.07，字母先呈现题目的正确率显著更大。其它主效应和交互效应均不显著。

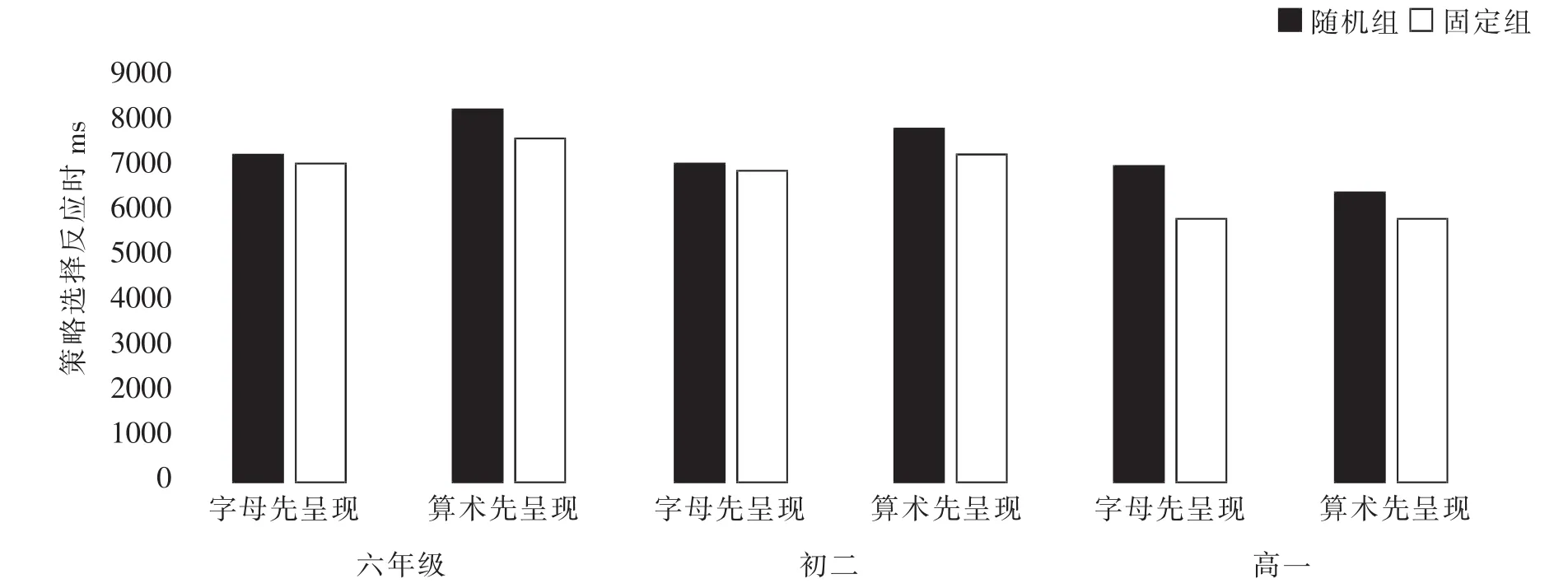
图3 任务呈现顺序、年级与任务呈现方式的交互作用图

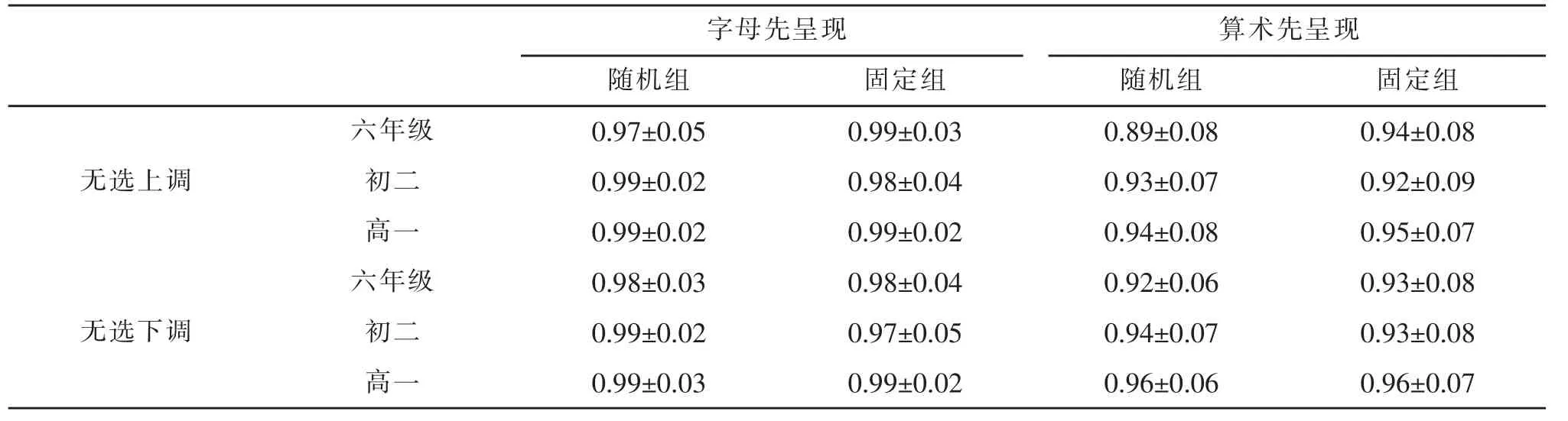
表5 无选条件下策略执行的正确率M±SD

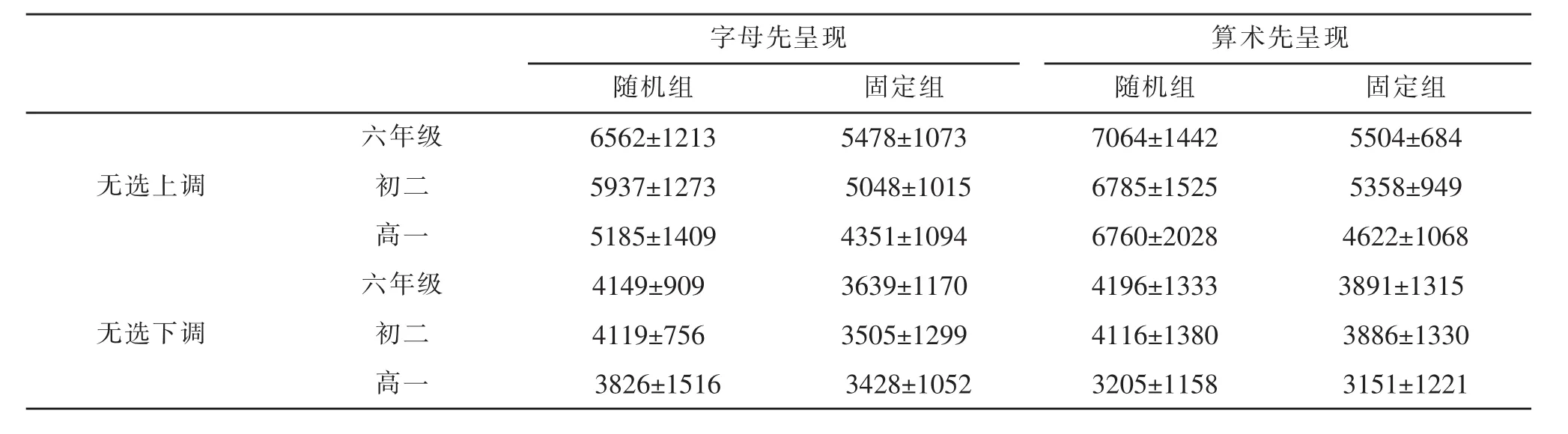
表6 无选条件下策略执行的反应时M±SD（单位：ms）

在反应时上：年级主效应显著，F（2，116）=7.60，p＜0.001，ηp2=0.12，Bonferroni事后检验发现，六年级显著大于高一（5109 vs.4276 ms），初二显著大于高一（4838 vs.4276 ms），六年级与初二差异不显著。策略运用条件主效应显著，F（1，116）=12.03，p＜0.01，ηp2=0.09，上调策略的执行反应时显著长于下调的反应时。任务呈现方式主效应显著，F（1，116）= 13.31，p＜0.001，ηp2=0.10，随机组的反应时显著长于固定组。任务呈现顺序与任务呈现方式交互作用显著，F（1，116）=5.80，p＜0.05，ηp2=0.05，简单效应分析发现，在随机组中，算术先呈现的策略执行反应时显著更长，F（1，121）=15.86，p＜0.001，ηp2=0.12，而在固定组中，差异不显著。策略运用条件与任务呈现方式交互作用显著，F（1，116）=70.24，p＜0.001，ηp2=0.34，简单效应分析发现，无选上调实验条件中，随机组的策略执行反应时显著大于固定组，F（1，121）=6.10，p＜0.05，ηp2=0.05，而在无选下调的实验条件下差异不显著。任务呈现顺序、策略运用条件与年级的交互作用显著，F（2，116）=5.19，p＜0.01，ηp2=0.08（见图4），对三因素交互作用进行简单简单效应分析，结果发现，在无选上调条件下，六年级在不同任务呈现顺序上的反应时没有差异，而初二（F（1，120）=5.48，p＜0.05）和高一（F（1，120）=14.47，p＜0.001）在算术先呈现的题目上策略执行反应时显著更长；在无选下调条件下，三个年级在不同任务呈现顺序上的反应时差异都不显著。其余主效应和交互作用均不显著。

4 讨论

本研究采用选择／无选法范式并结合改进后的PRP范式深入探讨了双任务协调影响算术计算策略运用的年龄特征。结果表明，任务呈现方式影响个体算术策略运用，表现为随机组的算术策略运用表现显著差于固定组；任务呈现顺序影响个体算术策略运用，表现为字母先呈现的算术策略运用表现显著差于算术先呈现；从六年级到高一阶段，青少年在双任务协调情境下的策略运用表现愈加出色。

图4 任务呈现顺序、策略运用条件与年级的交互作用图

4.1 双任务协调情境下青少年的策略运用

首先，本研究发现任务呈现方式影响个体策略运用，随机组个体的策略运用表现差于固定组。这一点符合研究假设，也与前人研究结果相一致［35］。从认知资源分配角度来看，个体在不知道任务出现顺序的情况下需要耗费额外的资源来关注任务出现的顺序，所以随机组中所需要的认知资源更多，而在固定顺序组中，个体已经预先知道了任务的出现顺序，这就使他们在实验开始前就形成了心理预期，心理预期减少了个体的认知资源的消耗［36］。这在一定程度上也验证了Szameitat，Schubert，Müller和Cramon的研究结果［22］。

其次，任务呈现顺序也影响了个体策略运用，表现为算术先呈现题目的策略运用表现差于字母先呈现题目。这可能是因为，在本研究中，首先呈现的任务是消失的，而第二个出现的任务直到对两个任务都做出反应后才消失，若先呈现估算任务，那么个体在进行估算时，需要对题目进行记忆题目并提取，这比字母先呈现的题目（估算题目不消失）占用了更多的认知资源，进而导致策略选择与执行效能低于字母先呈现的题目。

最后，本研究也发现执行上调策略比下调策略更难，这与没有涉及到双任务协调情境的先前相关研究相符。先前研究显示，个体在进行算术估算时，使用上调策略的反应时间明显长于下调策略且正确率更低［8，37］。这可能是因为使用上调策略时需要对两个操作数都进一位（如，34上调为40），其加工过程更复杂，消耗的认知资源更多。相比而言，下调策略更简单一些，只需将个位数舍去即可（如，34下调为30）。

4.2 双任务协调情境下青少年策略运用的年龄相关差异

从策略选择来看，总体来说，本研究发现相比低年级被试，高年级被试能够既快又准地做出策略选择（反应时短，正确率高）。Lemaire和Lecacheur的研究也发现了随着年龄的增长个体策略选择能力不断提高［2］，Hodzik和Lemaire也发现了类似结果［38］。我们认为原因可能来自两方面：（1）个体的算术能力可能会影响个体的策略选择［7］。本研究结果也显示了算术技能在策略选择正确率上的主效应，而高一学生的算术技能相对较高，因此能更准确地做出策略选择。国内学者刘伟方等人也发现算术知识在估算策略运用方面起到重要作用，同时他们还指出元认知监测对年龄差异的作用，随着年龄增长，元认知监测能力增强，个体策略选择能力也相应提高［39］。（2）执行功能中的抑制和认知灵活性与策略选择的年龄差异可能有密切关系。对于给定的题目，在选择最佳策略之前，个体必须抑制前一个策略并激活一个新的（或有时是相同的）策略［40］。从青少年早期到青少年晚期，个体的前额叶功能不断发展成熟［41］。受前额叶功能发展的影响，高一学生相对于其他两个年级的学生有着更强的认知灵活性和更有效的抑制能力，这使得高一学生能更容易地完成试次间策略的转换，从而有效避免重复效应。

当探讨个体在双任务协调情境下的策略执行表现时我们发现了相似结果。本研究结果显示随着年龄增长，不仅个体策略执行的速度加快，而且执行正确率也在不断提高，这与以往的研究结果一致［4］。王明怡与陈英和曾发现，中央执行的干扰造成了策略整体执行效果的下降［42］。在本实验中，儿童需要完成字母任务和算术任务，在完成字母任务的过程，中央执行在不停地进行执行、判断与监控，这些操作对算术认知加工造成严重干扰，这使得他们无法正确快速进行算术任务。随着年龄增长，个体工作记忆容量增加，信息加工速度也在提高，因此，年龄大的个体有更多的工作记忆资源用于认知加工，策略执行得也就越快越准。

此外，本研究还发现一个有趣的结果。在策略选择上，随机组中，六年级个体在双任务情境下不同任务呈现顺序题目上的反应时没有显著差异，而初二和高一算术先出现题目的反应时显著更长；在策略执行上，无选上调条件下，六年级在双任务情境下不同任务呈现顺序上的反应时没有差异，而初二和高一在算术先出现的题目上策略执行反应时显著更长。这似乎有悖常理，实则不然。根据认知负荷理论［43］，各种认知活动均需要消耗认知资源，从而产生一定的认知负荷，而个体的认知资源是有限的，若所有活动所需资源超过了工作记忆的容量，就会引起资源分配不足，从而影响个体的问题解决表现。已有研究发现估算策略的选择与执行需要占用工作记忆资源，而且复杂的策略比简单的策略占用的更多，难度大的问题比难度小的问题占用的也更多［30，44］。六年级个体没有差异，这可能恰恰是由于六年级个体认知资源相对较少与双任务协调能力差导致。具体来说，一方面，相比固定组或无选下调，在随机组或无选上调条件下，会占用个体更多的认知资源，这使得用于估算策略选择与执行的资源减少。另一方面，本研究在改进PRP双任务范式时，将原来范式中一种听觉任务和一种视觉任务，改进为两种视觉任务，这势必增加了协调两种任务的难度。相比初二与高一，六年级学生不但认知资源有限，而且双任务协调能力也差，这就会导致在需要占用额外认知资源的情境中（随机组或无选上调条件），不管在字母先呈现题目上还是算术先呈现题目上，个体的估算策略运用表现都很差，也会表现出在不同任务呈现顺序上的反应时没有差异。随着年龄增长，从六年级到高一，随着个体工作记忆容量增加，数字工作记忆广度也持续增长［45-47］，双任务协调能力也越来越好，因此，初二与高一学生反应时即开始出现差异，但是直到高一双任务协调能力还没有提升到能很好地协调两种认知任务的程度。

最后，本研究还发现，从双任务表现和策略运用表现来看，虽然随着年级的升高，青少年算术策略运用表现呈现出发展的趋势，但其中高一和初二、六年级的青少年算术策略运用表现的差别较大，而初二和高一青少年的算术策略运用表现的差别较小。这一方面可能与算术任务有关，算术任务为多位数运算任务，这不同于个位数简单加减运算任务。不同年级阶段的青少年可能对算术任务的熟悉程度是不同的，因此在实验过程中，如果不同年级阶段青少年对于干扰任务的加工再不同，那么这种复杂算术任务对于算术策略运用的考察便更敏感了。另一方面，这可能与双任务协调能力的发展有关。本研究发现，高一与初二、六年级双任务表现的差别较大，但是初二和高一青少年的算术策略运用表现的差别较小，初二到高一阶段双任务协调能力的提高使得个体能更好地同时处理两个任务，进而表现出在双任务情境下算术策略选择与执行得更快、更准。这也为本研究结果提供了支持。

综合本研究结果可发现，首先，任务呈现方式会影响不同年龄青少年在双任务情境下的估算策略运用。在固定呈现方式下，被试可以对下一任务产生有效的心理预期与准备，减少双任务协调时使用的认知资源，将更多的认知资源用于策略运用或其他认知过程。其次，任务呈现顺序也会影响不同年龄青少年在双任务情境下的估算策略运用。实际上，这也在一定程度上说明了任务消失与否对个体双任务协调情境下算术策略运用的影响。先呈现的任务消失势必会增加对认知资源的消耗，以至于影响双任务协调、策略运用等其他认知过程。因此，在双任务情境中，不能忽视双任务情境（包括任务呈现方式、顺序）对包括算术策略运用在内的其他认知过程影响。有研究者甚至发现通过改变任务情境，双任务协调过程中产生的认知消耗可以减少甚至消失［35］。因而，可以通过优化双任务情境，来促进个体在双任务情境下更好地完成任务。最后，本研究也发现，从六年级到高一，青少年的双任务表现越来越好，而且在双任务情境下的算术策略运用能力也有逐步提高的趋势，而且发展速度并不一致，初二到高一期间发展相对较快。这意味着，这一阶段的学生的双任务协调能力及其双任务协调时的算术策略运用等其他认知加工能力是有可塑性的。这就提醒广大教育工作者，在这一期间要注重提高学生相应的认知能力，而且研究者发现双任务协调能力是可以通过训练得到提高的［24］。因此，也可以通过提高双任务的协调能力，来促进个体在双任务情境下更好地完成任务。总之，不管是算术估算的策略运用，还是双任务协调对个体而言都是很重要的能力，但目前关于这两方面的探究还较少，研究者应加强相关研究，不断丰富理论结构及其实践应用。

1 Lemaire P.Executive functions and strategic aspects of arithmetic performance：The case of adults’and children’s arithmetic.Psychologica Belgica，2010，50（3＆4）：335-352.

2 Lemaire P，Lecacheur M.Age-related changes in children’s executive functions and strategy selection：A study in computational estimation.Cognitive Development，2011，26（3）：282-294.

3 Töllner T，Strobach T，Schubert T，et al.The effect of task order predictability in audio-visual dual task performance：Just a central capacity limitation？ Frontiers in Integrative Neuroscience，2012，6：1-13.

4 Lemaire P，Calliès S.Children’s strategies in complex arithmetic.Journal of Experimental Child Psychology，2009，103（1）：49-65.

5 Mata R，Schooler L J，Rieskamp J.The aging decision maker：Cognitive aging and the adaptive selection of decision strategies.Psychology and Aging，2007，22（4）：796-810.

6 Lemaire P， LecacheurM.Strategy switch costsin arithmetic problem solving.Memory and Cognition，2010，38（3）：322-332.

7 Torbeyns J，Verschael L，Ghesquière P.Simple addition strategies in a first-grade class with multiple strategy instruction.Cognition and Instruction，2005，23（1）：1-21.

8 Uittenhove K，Lemaire P.Sequential difficulty effects during strategy execution.ExperimentalPsychology，2012，59（5）：295-301.

9 Benjamin A S，Bird R.Metacognitive control of the spacing of study repetition.Journal of Memory and Language，2006，55（1）：126-137.

10 Son L K.Metacognitive control and the spacing effect. Journal of Experimental Psychology：Learning，Memory＆Cognition，2010，36（1）：255-262.

11 Hinault T，Dufau S，Lemaire P.Sequential modulations of poorer-strategy effects during strategy execution：An event-related potential study in arithmetic. Brain and Cognition，2014，91：123-130.

12 司继伟，杨佳，贾国敬，等.中央执行负荷对成人估算策略运用的影响.心理学报，2012，44（11）：1490-1500.

13 Imbo I，Vandierendonck A.The development of strategy use in elementary-school children：Working memory and individual differences.Journal of Experimental Child Psychology，2007，96（4）：284-309.

14 Imbo I，LeFevre J.Cultural differences in complex addition： EfficientChinese versusadaptive Belgians and Canadians.Journal ofExperimentalPsychology：Learning， Memory， and Cognition， 2009， 35（6）：1465-1476.

15 Imbo I， LeFevre J.Cultural differences in strategic behavior：A study in computational estimation.Journal of Experimental Psychology，Learning，Memory，and Cognition，2011，37（5）：1294-1301.

16 Collette F，Van der Linden M.Brain imaging of the central executive component of working memory.Neuroscience and Biobehavioral Reviews，2002，26（2）：105-125.

17 Liepelt R，Strobach T，Frensch P，et al.Improved intertask coordination after extensive dual-task practice. The Quarterly JournalofExperimentalPsychology，2011，64（7）：1251-1272.

18 Szameitat A J，Lepsien J，von Cramon D Y，et al. Task-order coordination in dual-task performance and the lateral prefrontal cortex：An event-related fMRI study.Psychological Research，2006，4（8）：1184-1199.

19 Schubert T，Fischer R，Stelzel C.Response activation in overlapping tasks and the response－selection bottleneck.Journal of Experimental Psychology：Human Perception and Performance，2008，34（2）：376-397.

20 陈英和，王明怡.儿童执行功能与算术认知策略的关系.心理科学，2009，32（1）：34-37.

21 杨佳，李颖慧，司继伟，等.工作记忆中央执行成分对估算表现的影响.心理学探新，2011，31（4）：314-317.

22 Szameitat A J，Schubert T，Müller K，et al.Localization of executive functions in dual－task performance with fMRI.Journal of Cognitive Neuroscience，2002，14（8）：1184-1199.

23 Hartley A A，Maquestiaux F.Success and failure at dual－task coordination by younger and older adults.Psychology and Aging，2007，22（2）：215-222.

24 Strobach T，Frensch P，Müller H，et al.Age－and practice－related influenceson dual－task costsand compensation mechanisms under optimal conditions of dual－task performance.Aging，Neuropsychology，and Cognition，2012，19（1）：222-247.

25 杨佳.中央执行负荷影响算术策略运用的年龄相关差异：以估算为例.山东师范大学硕士学位论文，2012.

26 司继伟.小学儿童估算能力研究.西南大学博士学位论文，2002.

27 Uittenhove K，Poletti C，Dufau S，et al.The time course of strategy sequential difficulty effects：An ERP study in arithmetic.Experimental Brain Research，2013，227（1）：1-8.

28 Siegler R S，Lemaire P.Older and younger adults’strategy choices in multiplication：Testing predictions of ASCM using the choice／no－choice method.Journal of Experimental Psychology：General，1997，126（1）：71-92.

29 Salminen T，Strobach T，Schubert T.On the impacts of working memory training on executive functioning.Frontiers in Human Neuroscience，2012，6（4）：81-89.

30 Imbo I，Duverne S， Lemaire P.Working memory，strategy execution， and strategyselection in mental arithmetic.Quarterly Journal Experimental Psychology，2007，60（9）：1246-1264.

31 French J W，Ekstrom R B，Price I A.Kit of reference tests for cognitive factors.Princeton，NJ：Educational Testing Service，1963.

32 Han S H，Kim M S.Visual search does not remain efficient when executive working memory is working. Psychological Science，2004，15（9）：623-628.

33 Smith－Chant B L，LeFevre J.Doing as they are told and telling it like it is：Self－reports in mental arithmetic.Memory＆Cognition，2003，31（4）：516-528.

34 Thevenot C，Fanget M F，Fayol M.Retrieval or nonretrieval strategies in mental arithmetic？ An operand recognition paradigm.Memory＆ Cognition，2007，35（6）：1344-1352.

35 Leonhard T，Ulrich R.Determinants of central processing order in psychological refractory period paradigms：Central arrival times，detection times，or preparation？ The Quarterly JournalofExperimental Psychology，2011，64（10）：2012-2043.

36 De Jong R.The role of preparation in overlapping－task performance.Quarterly Journal of Experimental Psychology，1995，48（1）：2-25.

37 Lemaire P， LecacheurM.Children’s strategies in computational estimation.Journal of Experimental Child Psychology，2002，82（4）：281-304.

38 Hodzik S，Lemaire P.Inhibition and shifting capacities mediate adults’age－related differences in strategy selection and repertoire.Acta Psychologica，2011，137（3）：335-344.

39 刘伟方，华晓腾，封洪敏，等.算术策略运用能力的年龄差异：元认知监测与算术知识的作用.心理发展与教育，2014，30（3）：234-243.

40 Vandamme K，Szmalec A，Liefooghe B，et al.Are voluntary switches corrected for repetitions？ Psychophysiology，2010，47（6）：1176-1181.

41 Best J R，Miller P H，Naglieri J A.Relations between executive function and academic achievement from ages 5 to 17 in a large，representative national sample.Learningand IndividualDifferences， 2011，21：327-336.

42 王明怡，陈英和.工作记忆中央执行对儿童算术认知策略的影响.心理发展与教育，2006，22（4）：24-28.

43 Cooper G，Sweller J.The effects of schema acquisition and role automation on mathematical problem solving transfer.Journal of Educational Psychology，1987，79（4）：347-362.

44 Ardiale E，Lemaire P.Within－item strategy switching：An age comparative study in adults.Psychology and Aging，2013，27：1138-1151.

45 段小菊，施建农，冉瑜英.8岁到成年期工作记忆广度的发展.心理科学，2009，32（2）：324-326.

46 李德明，陈天勇，李贵芸.认知能力的毕生发展及其分离性和个体差异性研究.心理科学，2004，27（6）：1288-1290.

47 李美华，白学军，沈德立.不同年级学生执行功能发展水平研究.心理科学，2008，29（3）：609-613.

Task-presented Mode and Task-presented Orders Influence the Age-related Differences of Arithmetic Strategy Use in Adolescents

Sun Yu，Lu Chun，Si Jiwei，Wang Tingting
（School of Psychology，Shandong Normal University，Jinan 250358）

Combining the PRP paradigm and the choice／no－choice method，the present study examined the age－related characteristics of dual－task coordination among different graders in strategy used by setting different task－presented modes（random mode vs.fixed mode）and task－presented orders（letters presented first vs.computational estimation presented first）.127 adolescents of different grades participated in this study.The main results showed that： （1）Task－presented modes influenced arithmetic strategy use in dual－task coordination.The estimation performances in the fixed mode were better than those in the random mode； （2）Task－presented orders influenced the use of arithmetic strategy in dual－task coordination.The performances of arithmetic strategy with letters presented first was poorer than those of arithmetic strategy with computational estimation presented first； （3）With the ascending of grade，the adolescents’ability of using arithmetic strategies was gradually improving，while the developing speed in different stages were different.

arithmetic strategy use；dual－task coordination；age－related characteristics；adolescents

国家自然科学基金项目（31371048）

司继伟，男，教授，博士。Email：sijiwei1974@126.com