陶瓷配方的优化计算方法

秦晓玲 / 上海市计量测试技术研究院

陶瓷配方的优化计算方法

秦晓玲 / 上海市计量测试技术研究院

根据优化设计的需要，在陶瓷配方设计中引入现代优化算法。以绝对误差为目标函数，建立了基于多目标优化的陶瓷配方优化设计数学模型，使陶瓷配方设计问题转变为以原料上下限为约束条件的求解极值问题。本文通过分析和合理选择样本数据，总结其中的数值规律，并使用MATLAB求得最优解，从而实现了陶瓷配方的优化设计。

优化算法；陶瓷配方；数学模型；MATLAB

0 引言

最优化计算方法在数学上是一种求极值的方法，以前解决最优化问题的数学方法只局限于古典求导方法和变分法（求无约束极值问题）拉格朗日乘数法解决等式约束下的条件极值问题。直到高速计算机的出现，人们才得以解决这类较大规模的优化问题，使最优化方法成为一种实用工具，因此最优化计算方法是近年来应用数学中发展最迅速的一个分支，现已渗透到科学、技术、工程、经济等各个领域。它不是传统的工程方法，却与技术和应用数学、计算机科学以及各专业领域都有密切的关系。材料科学作为一门新兴学科远不像数学、物理学那样有系统的理论和精确的数学方法，新材料、新物质的探索和研制常常是通过运用经验性方法，或称为“试错法”。陶土、釉料的配方研究至今仍基本上是一门试验科学，目前的专业理论尚不足以精确地预报这类材料的性能，因此需要通过大量的试验，摸索各种材料的性能与配比、结构与工艺条件之间的关系，继而在考虑成本、售价、利润等经济因素的约束条件下，最终计算出该材料的组成和原料成分比。可见试验方式十分繁琐且低效，因此，希望通过确定这些因素之间的数学关系，通过新的计算方法得出最优化的配比，从而可以摆脱这种复杂、低效的方式，这也是把最优化方法借助计算机这一现代化的工具应用到该领域中来的最主要目的。

1 设计优化计算方法

针对分析陶瓷成分这一点，无论是设计新材质的陶瓷配方，还是改进过的原配方，都不外乎其化学组成。传统陶瓷的组成一般来说主要是采用天然的岩石、矿物、黏土等材料作为原料。而新型陶瓷则是采用人工合成的高纯度无机化合物为原料，在严格控制的条件下经成型、烧结和其他处理而制成具有微细结晶组织的无机材料。近年来，有五种新型陶瓷受到市场的重视，也是今后分析计算的重点。

1）耐温陶瓷：日本研制出一种耐1 700 ℃以上高温的陶瓷，其是氧化铝粉末经熔化、冷却、再熔化后制成。它强度高，加工性能好，在高温下不会蜕变。

2）发光陶瓷：国外市场上的发光陶瓷是在瓷砖光泽釉表面使用丝网印刷办法，在所定图画下放以仅在紫外线照射下发生萤光的颜料，并选用荧光颜料与热固性树脂混合加热或在800 ℃下烘烤制成。该陶瓷用于室内外墙面点缀，具有良好的点缀效果。

3）超轻陶瓷：日本研制出一种比木头更轻、可浮于水上的超轻量陶瓷。它是将一种被称为“中空树脂填料”的材料按规定的份额同黏土掺和而成。用这种材料制成的陶瓷器，其比重下降至0.3，但其强度却与传统陶瓷无异。用这种超轻陶瓷材料烧制成的铺盖屋顶瓦片质量轻、耐地震，并且降低了运输成本。

4）木材陶瓷：美国科研人员发明了一种增强木材陶瓷。它是将木材浸入四乙氧基硅烷中，待吸足浸入液体后放入500 ℃的固化炉中，在炉内木材细胞内的热量和水分将四乙氧基硅烷烧结成陶瓷。与一般木材比较，其硬度更高，强度更高，是一种有广泛用途的点缀建材。

5）精密陶瓷：日本一公司研制出的这种新型建材精密陶瓷是一种主要由水溶性胶乳组成的粉末。如将100 g水泥与20 g细胞陶瓷在水解效果下构成混合物，便彻底消除了在水合效果过程中发生钙的自由度，可使水泥的寿命延长并且耐高温。当用非水模型(塑料制模)时，可得到与陶瓷相同的光泽。

综上所述，为研制这些新配方陶瓷，对其化学组成进行定量分析是非常关键的，当然其中还需要考虑到部分原料如矿物成分、微颗粒含量和胶体指数等不确定度对目标配方性能的影响。这些众多的影响因素在通常的陶瓷配方分析中往往难以顾全。陶瓷材料的分析过程是复杂多变的，目前没有通用的公式或数学模型来进行计算。因此，确定最终目标后，需要结合各种因素设计出最佳的分析方案，完成计算目标。

最优化计算方法解决实际问题一般分为五个步骤进行：

1）提出最优化问题，收集相关数据和资料；

2）给出最优化问题的数学模型,确定变量,列出目标函数和约束条件；

3）分析模型，选择合适的最优化及其求解方法；

4）编写程序求解，用计算机求最优解，本文所使用的是MATLAB；

5）最优解的检验和实施。

上述五个步骤中的工作相互支持和相互制约，在实践中常常是反复交叉进行。

1.1 建立优化设计的数学模型

在计算陶瓷配方的实验中，被用到的原料大多是天然的矿物或岩石原料，组成陶瓷配方原料的化学成份或物理性能指标与陶瓷配方绝大部分呈线性关系。因此本文采用含量配比的线性规划建立计算最佳陶瓷配方的数学模型，由此较为直观清楚地反应配料及原料的名称和用量。陶瓷原料化学组成配比计算问题的一般形式如表1所示。

这次建模试验中所取样的原材料及其配比如表2所示。

表1 陶瓷原料化学组成配比问题的一般形式

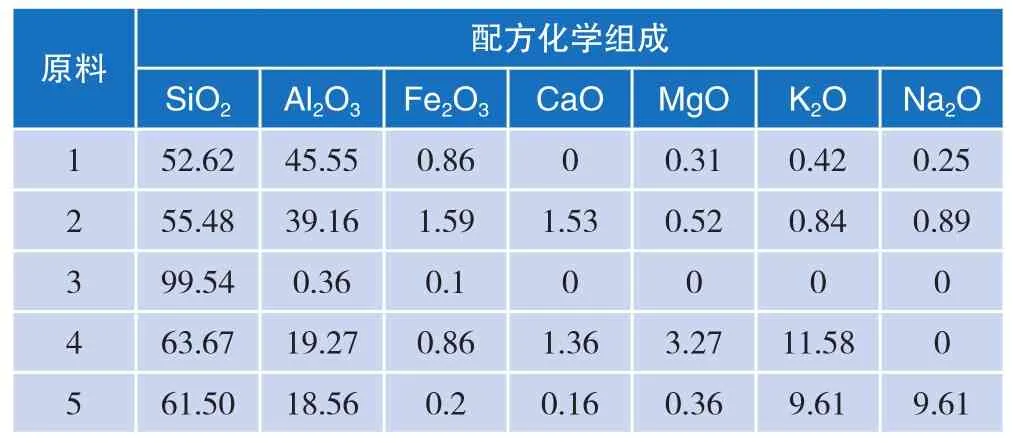
表2 选材组成

经过上述分析，陶瓷配方最优化计算的数学模型可归结为

1.2 分析模型并选择求解方法

分析原材料配比的需求是根据之前提出的最优化问题及目标确定的，因此优化目标是单一的，但考虑到原料的配比并不绝对相同，原料本身的属性、工艺参数的不确定度等都受工艺过程的影响很大，不同的工厂所生产出的原材料也不尽相同。因此，在这种情况下，需要通过约束条件加以解决。从该建模中可以看出，计算陶瓷配方问题的目标函数间具有一定的竞争关系，为了使其能一致地趋向各自的最优值，需采用统一目标函数法，根据具体情况再加权得出相对误差。这个方法的关键是加权因子的选择，本文随机选取两组因子，1号为化学成分含量因素，2号为价格因素。由此可以将原来的多目标优化问题转换为简便的单目标优化问题，如下所示：

式中：Wi，Wj—— 化学成分含量和原料的加权系数；

Yaj—— 第j个化学成分含量的目标值；

fi(x) —— 第i种原料的质量百分比；

Xaij—— 第i种原料中的第j个化学成分含量；

f(X) —— 加权后的统一目标函数值

由此，优化后的模型如下所示：

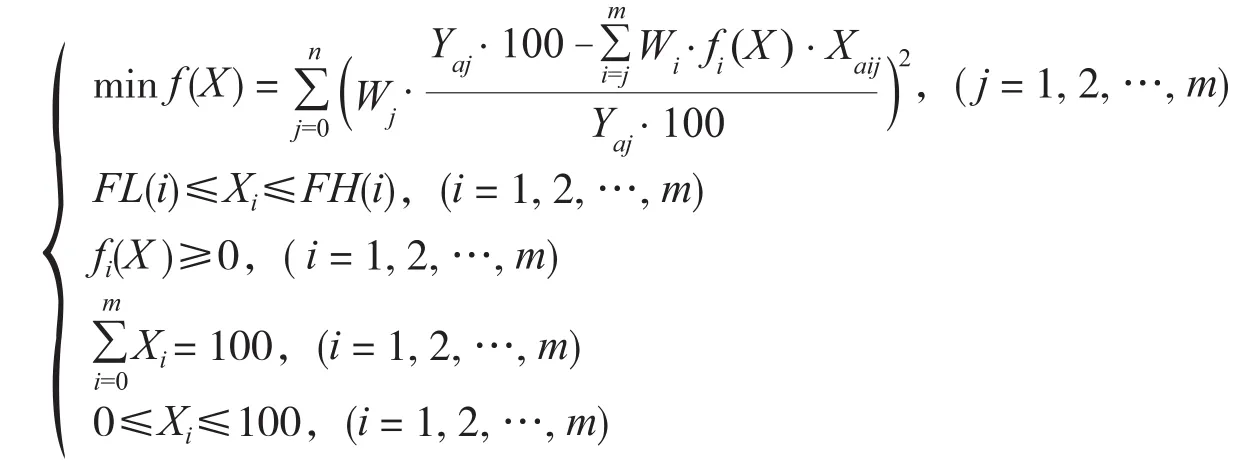
根据所选陶瓷原料的化学组成，计算其配料百分比。陶瓷原料总数为m，化学成分含量总数为n，然后将其组成一个m·n的矩阵。

1.3 计算及结果分析

陶瓷材料一般主要由 SiO2、Al2O3、Fe2O3、CaO、MgO、K2O、Na2O这七种化学物质组成，考虑到计算结果的稳定性，以追求无限接近预定值为目标，从而进行优化计算。MATLAB计算过程如下：

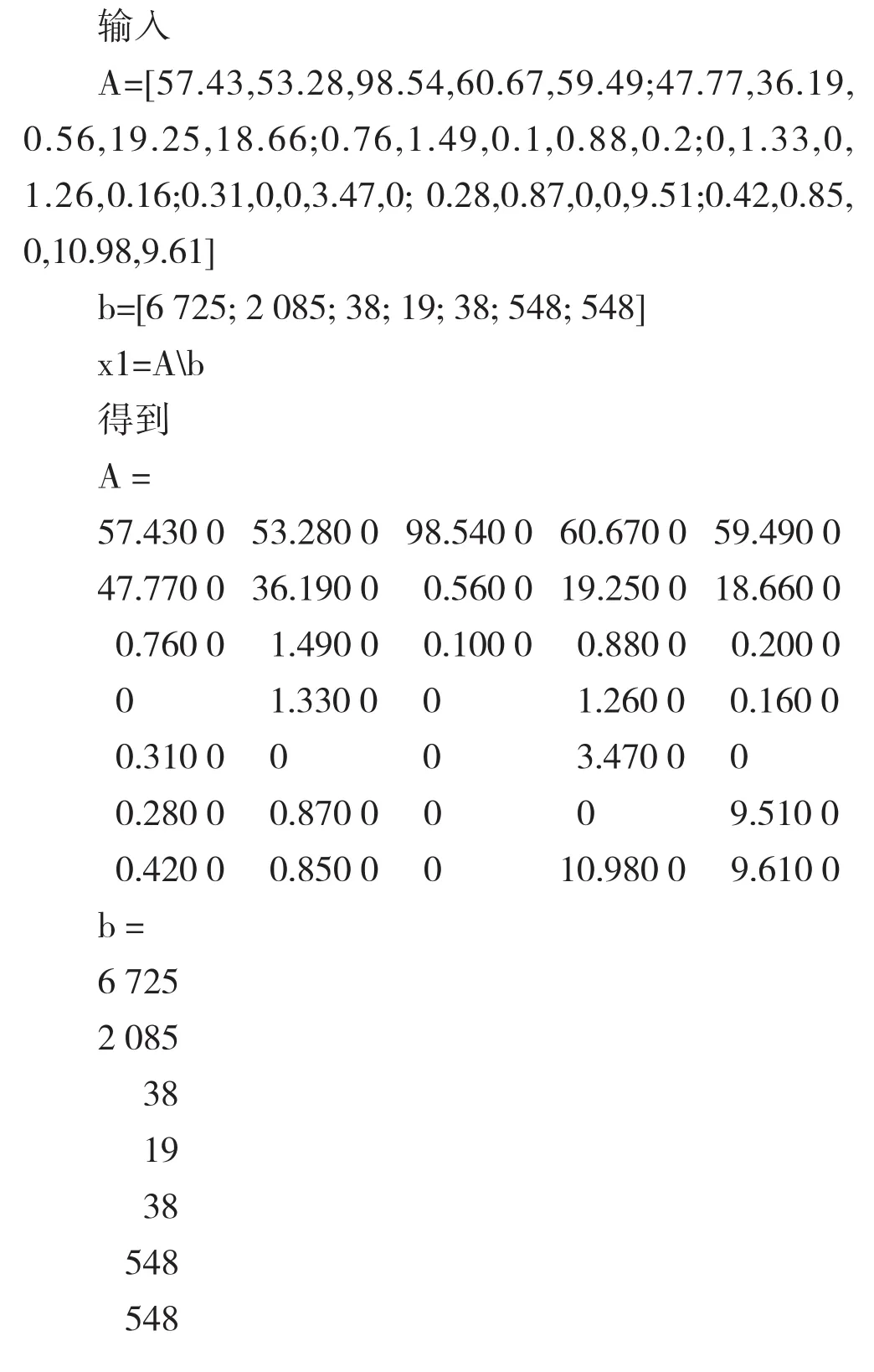
这是一个超定线性方程组，从计算结果可以看出，以绝对误差的综合作为目标函数，约束条件为原料上下限，各化学成分绝对误差都在2‰以内。显然，用最优化计算方法分析该材料既节约时间，亦可大大减少实验次数，非常适用于陶瓷材料的分析。需要说明的是，由于各种材料间的复杂性与多样性，可能某些计算值会出现偏差或无解，这时就需要重新设置约束条件后进行二次计算。

2 结语

应用最优化计算技术，在分析陶瓷配方中可以综合分析考虑影响配方的因素，这比常规计算方法所得出的结果要准确且更有效。同时通过此次建模计算可知，最优化计算是一种不可或缺的辅助手段，采用最优化计算方法不仅可以通过采集所需要的数据样本保证计算结果的可信度，更可以从多方面来体现其重要性和实用性；更可以根据分析前人积累的数据资料,发现数值之间的隐藏关系，进而用以指导科研计划,以及明确试验进行方向，甚至将该计算方法运用在工业化生产中的寻找优化区域等工作中。

[1]Douglas M.Bates.非线性回归分析及其应用[M].韦博诚译.北京：中国统计出版社，1997.

[2]陈念贻.模式识别优化技术及其应用[M].北京：中国石化出版社，1997.

[3]刘阳，曾令可.计算机在陶瓷配方设计中的应用[J].中国陶瓷工业，2002，2（9）：19-22.

[4]马致远.优化法在陶瓷釉料配方中的应用[J].佛山陶瓷，2005，2（15）：18-20.

[5]张纯禹.现代优化计算方法在材料最优化设计中的应用[J].中国陶瓷工业，2007，14（1）：23-26.

[6]杨云，黄亮.运动MATBAL实现对显微图片的数字化分析[J].机械设计与制造，2006（2）：135-137.

[7]王志强，姜群英，温其兵.陶瓷配方优化设计的通用方案开发[J].中国陶瓷，2001，4（37）：37-39.

[8]王冀海.最优化技术在陶瓷配方中的应用[J].中国陶瓷，1999，4（35）：18-35.

[9]邢文训,谢金星.现代优化计算方法[M].北京：清华大学出版社，1999.

Optimization calculation method of ceramics formulation

Qin Xiaoling

（Shanghai Institute of Measurement and Testing Technology）

According to the demand of optimization design, modern optimization algorithm is introduced in the optimization design of ceramics formulation.Taking the absolute error as an objective function, an optimization mathematical model of the ceramics formulation based on multi-objective optimization was built, which converts the design of ceramics formulation into the solution algorithm of extreme value by the constraint condition of upper and lower limit value of raw material.In the paper the sample data are analyzed and reasonably selected, the numerical rule of the sample data is summarized, and the optimal solution is obtained by MATLAB, which realizes the optimization design of ceramics formulation.

optimization algorithm; ceramics formulation; mathematical model; MATLAB