循环荷载下粉土液化流动特性拖球试验研究

刘涛, 张美鑫, 崔逢

(1.山东省海洋环境地质工程重点实验室，山东 青岛 266100；2.海洋环境与生态教育部重点实验室，山东 青岛 266100)

循环荷载下粉土液化流动特性拖球试验研究

刘涛1,2, 张美鑫1，2, 崔逢1，2

(1.山东省海洋环境地质工程重点实验室，山东 青岛 266100；2.海洋环境与生态教育部重点实验室，山东 青岛 266100)

基于流体力学中的Stokes黏滞阻力理论，以振动台试验为基础，开发了一套测量液化过程中粉土流变特性的拖球试验装置。在铺有粉土海床的模型箱内埋设光滑小球，通过测量小球水平运动过程中所受阻力值的大小，计算粉土液化的表观动力黏度，分析粉土液化过程中的表观动力黏度与超孔压比之间的关系，以及液化后表观黏度与应变率的变化规律。试验结果表明，振动台试验下，孔隙压力表现为迅速上升，粉土迅速达到液化状态；振动过程对海床固结影响较大；粉土海床在未达到完全液化状态时(ru<1)，表观黏度随超孔压比增大而减小，在液化状态下(ru=1)，剪应力随应变率增大而减小，粉土呈现出剪切稀化的特点，为典型的非牛顿流体特征。

粉质土；液化；流动特性；拖球试验；振动台试验

1 引言

现代黄河水下三角洲海床沉积物主要由高泥沙含量河流在入海口快速堆积形成的粉土构成[1]，具有高含水率、欠固结等特点[2]。该类土在波浪循环荷载作用下极易发生液化，可能诱发海床失稳、海底滑坡、海底管线破坏等，对于海上建筑有着极大的危害[3—5]。

针对土体液化的研究，日本学者Sasaki等[6]在一系列振动台试验的基础上，对砂土液化变形的发生机理进行了研究，发现液化土体有着与黏性流体十分类似的特征，并提出液化后砂土具有流动特性这一观点。随后，Hamada和Wakamatsu[7]针对1980-1990年间发生于日本的地震进行汇总分析，通过多次振动台试验，分析了土体液化的流动和移动的特点，认为液化土体流动存在与亚塑性流体相似的特点。Uzuoka等[8]将液化土体假设为一种存在屈服强度的非牛顿Bingham流体，通过考虑土体的屈服强度值，提出了等效黏滞度的概念，利用压力耦合公式求解斯托克斯公式，并实现了有限差分的求解，基于此建立了非牛顿流体的模型。刘汉龙等[9—10]进行了大量砂土液化大变形室内试验，根据结果初步提出了一个反映砂土液化应力-应变关系的双曲线模型，并且通过验证得出该模型与试验结果较吻合的结论。陈育民等[11]通过一些列室内模拟试验发现，液化状态的砂土是一种“剪切稀化”非牛顿流体，可用幂律方程来表示其本构关系，试验发现液化后的砂土能够产生较大的位移变形。刘涛等[12]以黄河口粉质土为研究对象，对波浪作用下粉土液化过程进行了分析，综合考虑试验中波浪要素、超孔压比等因素的影响，得出了液化粉土黏度随液化程度的变化趋势。

目前有关液化土体性状的研究大多局限于砂土[13—14]，而针对粉质土液化的研究，尤其是黄河口地区沉积物快速液化过程中土体性状的研究成果尚不多。在粉质土液化流变的前期研究中，虽然给出了表观黏度随液化程度的变化，但仍存在一定的局限性。本文通过设计振动台模型箱试验，分析粉土液化过程中的表观黏度与超孔压比之间的关系，以及液化后表观黏度与应变率的变化规律。

2 试验设计与试验内容

2.1 试验装置

本次试验所使用的振动台位于中国海洋大学工程学院实验室，振动台的主要技术参数如下：台面尺寸1 m×1 m(长×宽)；振动频率：60 Hz；振幅：5 mm；电机功率：1.5 kW。

为防止模型箱在装满粉土时受压变形，造成孔压从边壁的消散，选用强度较大、不易发生形变的铁箱作为试验所用模型箱。模型箱尺寸为60 cm(L)×40 cm(W)×40 cm(H)，在连接缝处涂抹环氧树脂胶水，从而提高模型箱的防水性能，振动台及模型箱如图1所示。

图1 振动台及模型箱Fig.1 Shaking table and the test box

依据模型箱尺寸，设计加工了测定流动土体黏度的拖球试验装置，如图2所示。该拖球装置置于模型箱内部，支架内侧固定有3个定滑轮和1个小型绞车，钢丝绳穿过定滑轮和绞车连接小球。通过手动控制绞车能够使小球在土体中匀速运动，并能实现正反转动。小球直径1.5 cm，埋深距海床面15 cm。拉力传感器位于支架的上部，用来测量试验过程中的拉力值。

土层中埋设土压力传感器和孔隙压力传感器，分别用于测量土体总压力和孔压，传感器布设如图2所示。其中深度D1与小球处于同一水平高度，深度D2距离模型箱底部10 cm，D1、D2相距10 cm。

图2 试验装置示意图Fig.2 Schematic diagram of test equipment

2.2 试验土样

试验用土选自黄河水下三角洲地区的粉土，土体重度γ=19.0 kN/m3，含水率ω=25%，液限ωL=20.1%，塑限ωP=13.2%，塑性指数IP=6.9。土样颗粒级配曲线如图3所示。

图3 粉土颗粒级配曲线Fig.3 Silt particle size distribution curve

实验过程中发现在高频的振动下，容器的侧壁会很快的形成排水通道，土中的水会很快的从侧壁涌出，影响数据测量的真实性。为提高土体抵抗振动液化的能力，在底层和顶层的粉土中掺入少量高岭土，使其土样配比仍处于粉质土范围内，颗分曲线如图4所示。

图4 掺杂高岭土的土样颗分曲线Fig.4 Doping kaolin soil particles curve points

2.3 试验方法

(1)制作海床前，按照预设高度将孔压、土压传感器和拖球装置固定在模型箱中，调整箱内走线，以减小走线对试验的影响。

(2)海床制备。首先，按照一定比例把土样与纯高岭土混合，加水混匀，均匀的铺设在模型箱的底层，铺设厚度约5 cm，让其自然固结1 d；中间土样首先使用搅拌机搅拌均匀，海床高度为25 cm，由于海床较松散，存在自重固结，因此海床埋设过程中，初始高度略高于拟定高度，之后固结1周；最后在表层铺设与底层相同的掺杂了高岭土的粉土，海床整体高度高于35 cm，形成表层非液化层。上部非液化层表面平整，不存在斜状面。

(3)试验前使海床静置固结5 d，由于振动台振动频率较大，模型箱表层的积水容易在振动下溅出，试验前需把水排出部分，确保不会影响试验观测人员操作的方便。

(4)振动前需要对孔压、土压初值进行记录，由于振动台振动频率较大，因此每次振动施加约20 s便停止，过程中持续记录孔压、土压数据变化，振动停止后马上通过拖球装置进行测量，记录拉力值、小球运动距离及运动时间。

振动台每次振动强烈，小球重复拖动形成的运动轨迹在下次振动中均可振动均匀，因此对试验结果不会有影响。

3 试验结果分析

3.1 试验阻力分析

由于试验装置设计较为复杂，拉动小球运动的过程中，钢丝绳与滑轮之间、钢丝绳与粉土之间都会产生摩擦阻力。因此拉力传感器测量到的数值除了小球在运动过程所受土层阻力值，还包括试验装置中的构件摩擦力值。为减小试验误差，一方面在滑轮、钢丝绳上涂抹凡士林用于润滑；另一方面要测量装置的摩擦阻力。在没有小球的情况下进行拉动，可认为传感器测到的数据为试验装置的摩擦力，且试验过程中摩擦力保持恒定。3次空拉摩擦力值见表1，可以认为摩擦力值恒定为25 N。

表1 空拉阻力值

图5为一次振动试验过程中的拉力值时程曲线，小球拖动过程中拉力值逐渐增大并维持恒定，拖动结束后拉力值迅速减小。数据处理时选择拉力值较稳定的一段作为小球运动过程中所受阻力。

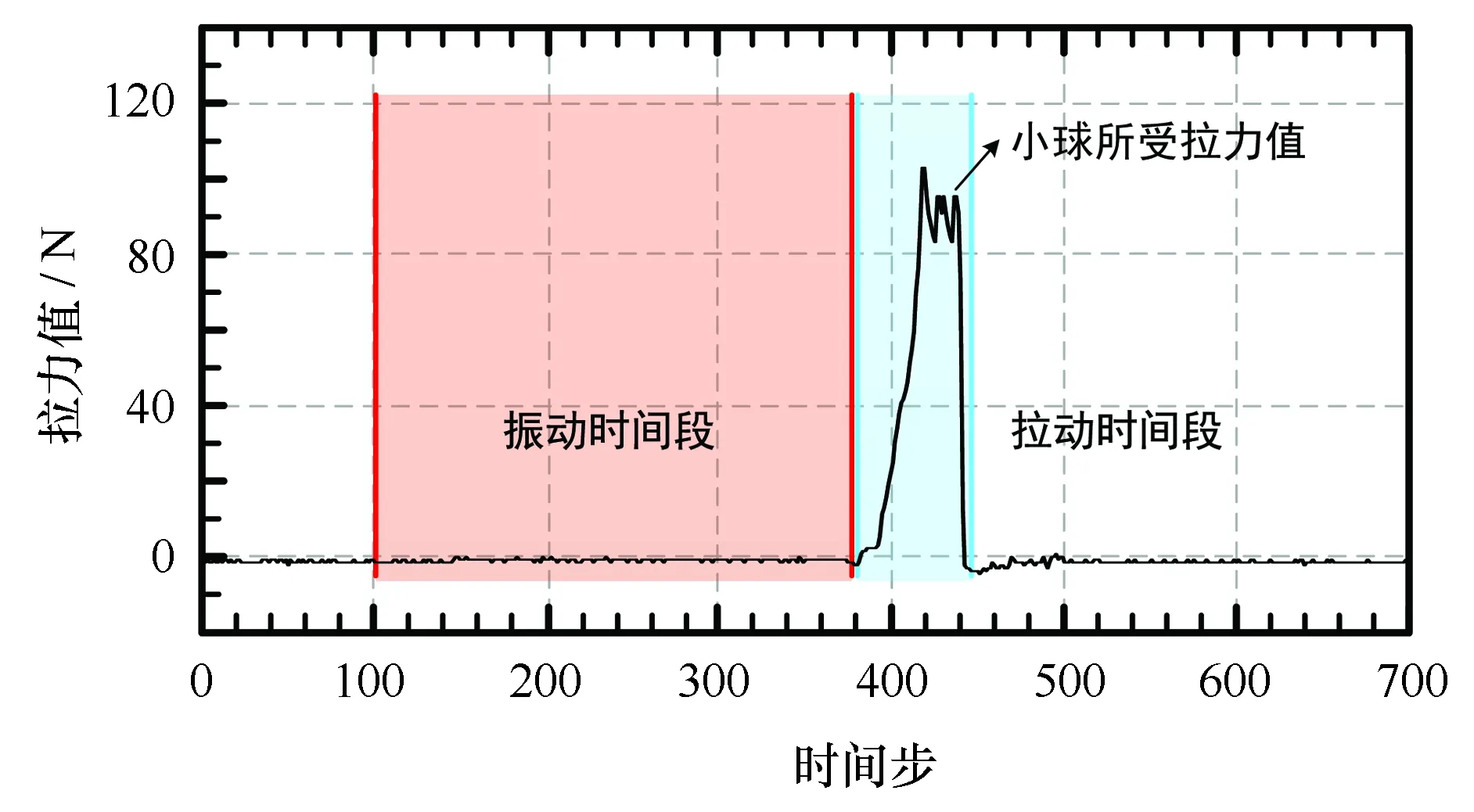
图5 拉力值时程曲线Fig.5 Rally value time curve

3.2 试验压力分析

图6和图7分别为某一组振动试验过程中土压力传感器和孔隙压力传感器测到的数据。首先由图6来分析试验过程中土体总压力变化情况。在D1深度处，即与小球处于同一高度处的总压力维持在2.0 kPa，D2深度处总压力维持在3.7 kPa左右。振动台对海床垂直方向施加的循环荷载对总压力基本没有影响，总压力可以维持在较为稳定的状态，直至试验结束。因此超孔压比可以用此土压传感器测量得到的数据进行计算。

图6 土压力时程曲线Fig.6 Earth pressure time curve

从图7中可以发现孔隙水压力在振动荷载下的累积，一段时间后能够达到液化，并且孔压能够一直保持在较高的水平。振动开始后，孔隙水压力值迅速上升，振动结束后，孔压不会马上消散，在一段时间内维持在较高水平。由于P2传感器所在位置更靠近底板，振动荷载由下向上传播，因此D2深度处的孔隙水压力升高速度更快。

图7 孔隙水压力时程曲线Fig.7 Pore pressure time curve

在振动试验过程中，振动循环次数对孔隙水压力的响应能产生一定的影响，从图7中可知，虽然振动循环次数对孔隙水压力沿海床深度方向分布趋势影响有限，但孔隙水压力最大振幅会随着振动循环次数的增加而增加。然而，振动循环次数对孔隙压力平均值几乎无影响。造成孔隙水压力最大振幅值随循环次数变化的原因在于，海床会在荷载施加后出现沉降现象。针对本次试验具体来说，海床的初始高度是35 cm，随着荷载的施加而出现不稳定现象即液化，并最终造成海床沉降，而海床沉降的发生将导致海床相对深度变小，由于孔隙水压力平均值并不随循环次数的变化而变化，因此海床相对深度的减小将最终造成孔隙水压力最大振幅值的减小。

图8为测量连续两次施加振动荷载时孔压值的变化曲线，测量的传感器为P2孔压传感器，测量深度为距海床面25 cm。第一次施加振动时间较短，在振动过程中观察到土体孔压值不断变化，这一过程中既有孔压积累又有消散，总体呈现孔压上升变化趋势。振动停止后，孔压迅速消散，并在较短时间内下降到初始值附近；随后开始施加第二次振动荷载，此次持续时间较长，由于初次振动使得土体密实，因此第二次振动过程中孔压升高曲线明显变缓，且升高到最大值后可以维持较高的孔压值不变，由于测量时间有限，没有观察到此次孔压值下降的曲线变化。

图8 P2传感器连续两次振动孔压曲线Fig.8 P2 vibration sensor twice pore pressure curve

3.3 振动对海床固结的影响

在均匀土试验中，海床高度会随着循环振动荷载的施加而往复变化，并最终出现一定沉降。为了更清晰的研究试验过程中海床沉降现象，采用千分尺对海床沉降过程进行了详细的记录。如图9所示，海床初始高度为38 cm，静置过程中由于自重固结使海床产生沉降，最终海床高度维持在35 cm；随着振动荷载的施加，海床高度突降并出现不稳定情况，逐渐产生变化最终出现一定的沉降，图10清晰地记录了振动荷载下海床沉降的情况。

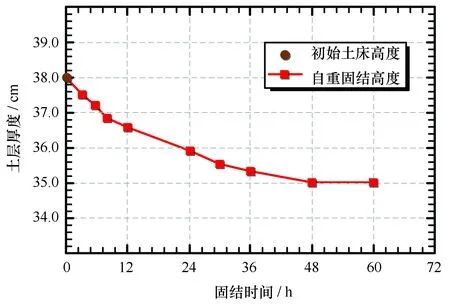
图9 土体自重固结Fig.9 Soil gravity consolidation

图10 土体振动固结Fig.10 Soil vibration consolidation

造成海床沉降的基本原因可以归结为以下两点：第一个也是重要的原因是海床液化过程中的孔压积累与消散。在孔压累积过程中，同时存在着孔压消散过程，有一部分孔隙水排出，孔隙空间减小，导致海床沉降。沉降量的大小取决于土的渗透系数和松散程度[17—18]。海床液化过程中的孔压积累与消散和海床沉降现象相互关联。第二个原因是循环振动荷载的施加使海床土颗粒之间孔隙体积减小造成海床相对密度的变化。

3.4 黏度特性分析

针对未达到液化的过程，为了分析超孔压比对液化粉土表观动力黏度的影响，选用同一天进行的多组试验数据进行分析，可以认为这组数据是在相对密度相差不大的情况下得到的，因此可以假设为在相同初始相对密度下的试验结果。图11为表观动力黏度随超孔压比的变化曲线，从图中可见，其两者关系十分明显，随着超孔压比升高(超孔压比ru<1)，表观动力黏度不断减小。土体的有效应力尚未达到0即尚未完全液化时，土体处于一种半流体的状态，而此时超孔压比已经增大到一定程度，土体表现为黏度的减小以及变形能力的增加。随着超孔压比升高，曲线不断变缓，也就是说表观动力黏度减小的速度减慢，说明土体的液化是一种渐变的过程，土体的孔隙水压力值不断上升直至引起土体模量的下降，最终完全液化，并体现出剪切稀化的非牛顿流变的特性。

图11 超孔压比(ru<1时)对表观动力黏度的影响Fig.11 Effect of excess pore pressure ratio of the apparent kinematic viscosity

在完全液化状态(ru=1)时，分析其应变率与剪应力的关系如图12所示，随着应变率增大，剪应力增长速度逐渐减缓。

图12 ru =1时剪应力-应变率的关系曲线Fig.12 The shear stress-strain rate curve(ru=1)

图13 ru=1时应变率-表观动力黏度的关系曲线Fig.13 The strain rate-apparent viscosity curve(ru=1)

根据剪应力-应变率的关系可以计算出表观动力黏度值。从图13中可以看出，对于液化后土体，表观黏度随着应变率的增大而逐渐减小，且变化趋势逐渐变缓，呈现出“剪切稀化”的特征。

4 结论

通过室内振动台下的拖球试验，得到试验结果如下：

(1)开发了一套可用于测量粉土液化过程中流动特性的拖球装置，通过小型振动台进行了液化粉土拖球试验，验证了拖球装置的可靠性。

(2)振动台试验下，孔隙压力表现为迅速上升，粉土迅速达到液化状态；试验中海床存在固结现象，振动过程对固结影响较大。

(3)通过拖球运动获得了液化粉土的黏度值，并对其黏度特性进行分析，在未达到完全液化状态(ru<1)时，表观黏度随超孔压比增大而减小；在液化状态(ru=1)时，剪应力随应变率增大而减小，粉土呈现出剪切稀化的特点，为典型的非牛顿流体特征。

[1] Prior D B, Suhayda J N, Lu N Z, et al. Storm wave reactivation of a submarine landslide[J]. Nature, 1989, 341(7): 47-50.

[2] 刘涛, 冯秀丽. 黄河水下三角洲低角度斜坡失稳模式探讨[C]//渤海湾油气田勘探开发技术论文集. 北京：中国石化出版社, 2010(7): 72-78.

Liu Tao, Feng Xiuli. Slope failure mode of low angle on Yellow River Delta[C]//Bohai Bay Oil and Field Exploration and Development Technology Proceedings. Beijing: China Petrochemical Press, 2010(7): 72-78.

[3] Pratson L F, Imran J, Hutton E, et al. Lagrangian model of subaqueous turbid surges[J]. Computers & Geosciences, 2008, 27: 701-716

[4] 孙永福, 董立峰, 宋玉鹏. 黄河水下三角洲粉质土扰动土层特征及成因探析[J]. 岩土力学, 2008, 29(6): 1494-1499.

Sun Yongfu, Dong Lifeng, Song Yupeng. Analysis of characteristics and formation of disturbed soil on subaqueous delta of Yellow River[J]. Rock and Soil Mechanics, 2008, 29(6): 1494-1499.

[5] 王良民, 叶剑红, 朱长歧. 近海欠密实砂质海床内波致渐进液化特征研究[J]. 岩土力学, 2015, 12(36): 3583-3588.

Wang Liangmin, Ye Jianhong, Zhu Changqi. Investigation on the wave-induced progressive liquefaction of offshore loosely deposited sandy seabed[J]. Rock and Soil Mechanics, 2015, 12(36): 3583-3588.

[6] Sasaki Y, Towhata I, Tokida K I, et al. Mechanism of permanent displacement of ground caused by seismic liquefaction[J]. Soils and Foundations, 1992, 32(3): 79-96.

[7] Hamada M, Wakamatsu K. A study on ground displacement caused by soil liquefaction[J]. Journal of Geotechnical Engineering, 1998, 43: 189-208.

[8] Uzuoka R, Yashima A, Kawakami T, et al. Fluid dynamics based prediction of liquefaction induced lateral spreading[J]. Computers and Geotechnics, 1998, 22(3): 243-282.

[9] 刘汉龙, 陈育民. 砂土液化后流动特性分析[C]//第一届全国岩土本构理论研讨会论文集. 北京:北京航空航天大学出版社, 2008.

Liu Hanlong, Chen Yumin. Analysis on flow characteristics of dynamic tests on post liquefied sand[C]//Symposium of the First National Geomaterial Seminar. Beijing: Beihang University Press, 2008.

[10] 陈育民, 刘汉龙, 邵建国, 等. 砂土液化及液化后流动特性试验研究[J]. 岩土工程学报, 2009, 31(9): 1408-1413.

Chen Yumin, Liu Hanlong, Shao Jianguo, et al. Laboratory tests on flow characteristics of liquefied and post-liquefied sand[J]. Rock and Soil Mechanics, 2009, 31(9): 1408-1413.

[11] 陈育民, 高星, 刘汉龙. 砂土液化流动变形的简化方法[J]. 岩土力学, 2013(6): 1567-1573.

Chen Yumin, Gao Xing, Liu Hanlong. Simplified method of flow deformation induced by liquefied sand[J]. Rock and Soil Mechanics, 2013(6): 1567-1573.

[12] 刘涛, 崔逢, 张美鑫. 波浪作用下液化粉土流动特性拖球试验研究[J]. 海洋学报, 2016, 38(3): 123-130.

Liu Tao, Cui Feng, Zhang Meixin. Dragging ball test on flow characteristics of liquefied silt under wave loading[J]. Haiyang Xuebao, 2016, 38(3): 123-130.

[13] Ye Jianhong, Wang Gang. Seismic dynamics of offshore breakwater on liquefiable seabed foundation[J]. Soil Dynamics and Earthquake Engineering, 2015, 76: 86-99.

[14] Ye Jianhong, Wang Gang. Numerical simulation of seismic liquefaction mechanism in Quaternary loose seabed[J]. Bulletin of Engineering Geology and the Environment, 2016, 75:1183-1197.

[15] Vanneste M, Sultan N, Sebastian Garziglia, et al. Seafloor instabilities and sediment deformation processes: The need for integrated, multi-disciplinary investigations[J]. Marine Geology, 2014, 352: 183-214.

[16] 杨少丽, 沈渭铨, 杨作升. 波浪作用下海底粉砂液化的机理分析[J]. 岩土工程学报, 1995, 17(4): 28-37.

Yang Shaoli, Shen Weiquan, Yang Zuosheng. The mechanism analysis of seafloor silt liquefaction under wave loads[J]. Chinese Jounal of Geotechnical Engineering, 1995, 17(4): 28-37.

[17] Zen K, Yamazaki H. Mechanism of wave-induced liquefaction and densification in seabed[J]. Soils and Foundations, 1990, 30(4): 90-104.

[18] Jeng Dongsheng. Wave-induced seabed instability in front of a break water[D]. Perth: The University of Western Australia, 1997.

崔万松，潘德炉，白雁, 等. 南海北部表层颗粒有机碳的季节和年际变化遥感分析[J]. 海洋学报, 2017, 39(3): 122-134, doi: 10.3969/j.issn.0253-4193.2017.03.012

Cui Wansong, Pan Delu, Bai Yan, et al. Satellite views of the seasonal and interannual variations of the particulate organic carbon in the northern South China Sea[J]. Haiyang Xuebao, 2017, 39(3): 122-134, doi:10.3969/j.issn.0253-4193.2017.03.012

Dragging ball test on flow characteristics of liquefied silt under cyclic loading

Liu Tao1,2, Zhang Meixin1，2, Cui Feng1，2

(1.ShandongProvincialKeyLaboratoryofMarineEnvironmentandGeologicalEngineering,Qingdao266100,China; 2.KeyLaboratoryofOceanEnvironmentandEcology,MinistryofEducation,Qingdao266100,China)

According to the theory of Stokes Law, the test apparatus of flow characteristics of liquefied silt is developed based on the shaking table tests. A steel sphere, embedded in the test box, can be moved in the horizontal direction when the silt liquefaction occurs. Resistance force and velocity of the steel sphere are measured during sphere dragging, then apparent viscosity can be evaluated. Analysis the relationship between apparent viscosity and excess pore pressure ratio during silty liquefaction. The change of apparent viscosity and strain rate after silty liquefaction is researched. The result shows that, during the shaking table test, the pore pressure showed a rapid increase, and silt quickly reached a liquefied state; there was consolidation phenomenon in the soil bed, and vibration had a great influence on consolidation. Analysis found that, when the soil has not reached completely liquefied state (ru<1), the apparent viscosity decreases with increasing of excess pore pressure ratio; when it has reached liquefied state (ru=1), the shear stress decreases with increasing of strain rate, the silt is shear thinning non-Newtonian fluid.

silt; liquefaction; fluid; dragging ball test; shaking table test

2016-05-23；

2016-10-19。

国家自然科学基金(41672272，41427803)；中央高校基本科研业务费专项资助项目(201564017)。

刘涛(1979—)，男，山东省高唐县人，副教授，主要从事海洋工程地质和海底灾害观测等方面教学与科研工作。E-mail：ltmilan@ouc.edu.cn.com

P642.1

A

0253-4193(2017)03-0115-07