基于能量方法的拉索尾流驰振风洞试验研究
吴其林, 华旭刚, 胡腾飞
(1.湖南大学 风工程与桥梁工程湖南省重点实验室,长沙 410082;2. 广西交通科学研究院,南宁 530007)
基于能量方法的拉索尾流驰振风洞试验研究
吴其林1, 华旭刚1, 胡腾飞2
(1.湖南大学 风工程与桥梁工程湖南省重点实验室,长沙 410082;2. 广西交通科学研究院,南宁 530007)
为了研究近距失稳区并列拉索尾流驰振性能,发展了基于能量方法的风洞试验方法。采用强迫振动装置重现了拉索尾流驰振现象,通过能量判断方法分析了下游拉索尾流驰振的运动方向和不稳定区域。从气动力对下游拉索做功的角度,研究了其振动机理,并对比分析了下游拉索不同振幅、来流风速以及频率对尾流驰振性能的影响。试验研究表明,基于能量分析方法所得到的结果与已有结论较为吻合,验证了该方法的可靠性。
并列拉索;尾流驰振;能量分析方法;风洞试验;强迫振动
拉索尾流驰振是指并列拉索沿风向斜列布置时,流经上游拉索后的尾流激起下游拉索振动的一种风致振动现象[1]。根据尾流驰振发生区域,可分为近距失稳区、稳定区和远距失稳区[2-3],当下游拉索超过上游拉索尾流影响区域时,尾流驰振不会发生。尾流驰振可能引起结构端部构件的疲劳开裂、严重时可能导致安装的阻尼器脱落,甚至发生两索相互碰撞的情况[4-5]。
目前,国内外学者对双圆柱尾流驰振进行了大量研究,其主要研究方法有风洞试验、理论分析与数值模拟及其交叉运用。ZDRAVKOVICH[6]认为并列圆柱间的流体形态与其相对位置有关,并将流体划分为近距干扰和尾流干扰两种类型;TOKORO等[7-8]采用气弹模型风洞试验分别对串列吊索和串列主缆进行了研究,两者均观在15°风攻角下观测到下游索(缆)以一阶模态振动为主的尾流驰振现象;李永乐等[9]通过尾流驰振风洞试验对斜拉桥并列拉索的远距失稳区进行了相关研究;而DIANA等[10-12]通过风洞试验与数值模拟方法对四分裂导线次档距振荡的尾流驰振特性进行了研究;黄伟峰等[13-14]采用数值模拟方法计算了并列索不同位置的静气动力系数,并分别采用两自由度准定常理论和单自由度驰振理论分析了下游索的失稳区域与临界风速;唐浩俊等[15]则采用基于能量方法的数值模拟对塔周长吊索远距失稳区的尾流驰振性能进行了研究。
以上学者大多都是通过风洞试验或数值模拟方法得到作用在拉索上的静气动力系数后采用理论分析方法对下游拉索的起振风速与失稳区域进行预测,或者通过气弹模型试验对下游拉索的起振风速与失稳区域进行直观判断,但前者仅从拉索的受力进行预测,而后者也只是通过测振来对临界风速作出判定,然而两者并未把发生尾流驰振时作用在拉索上的动态风荷载和动态位移有效联系起来,因此上述方法只能反映出尾流驰振的某些特性,而对其机理无法进行解释。尽管唐浩俊采用数值模拟方法从气动力输入能量的角度研究了尾流驰振性能及其机理,但尚未得到试验或事实证明,其准确性还有待进一步研究。因此,本文通过强迫振动风洞试验模拟了并列双圆柱索典型尾流驰振(近距失稳)现象,从气动力对拉索做功的角度出发,利用时域积分方法计算和分析得到下游拉索的运动方向及驰振失稳区域,并对尾流驰振的机理展开了研究,最后探讨了拉索振动幅值、来流风速以及频率对尾流驰振性能的影响。
1 尾流驰振能量判断法
拉索发生尾流驰振时,作用在拉索上的气动力做功要大于拉索自身振动所耗散的能量。因此,通过时域积分方法计算下游拉索平均单个振动周期内气动力输入的能量,并偏安全地忽略拉索由于自身阻尼所消耗的能量,以此来判断尾流驰振的发生。
考虑到采用能量分析方法对尾流驰振机理进行研究时应当侧重于振动的初始阶段,而在尾流驰振初期,拉索振幅通常很小,故强迫振动试验中下游拉索振幅应当采用较小值。同时考虑到尾流驰振由描述平均气动力现象的参数决定,因此下游拉索强迫振动的频率要小于自身及上游拉索的漩涡脱落频率。
采用强迫振动装置迫使下游拉索在均匀的横风下做稳态椭圆轨道的受迫振动,并同步记录拉索振动过程中力与位移的时程曲线,拉索能量的输入或耗散可以通过时域积分方法分别计算平均单个振动周期内阻力和升力对拉索所做的功,采用无量纲形式表示
(1)
(2)
式中:FD和FL分别为t时刻拉索所受的阻力与升力;x、y分别为拉索在直角坐标系中的位移;n为计算周期数并取整(n=26);T为振动周期(T=2.174 s);H为节段模型长度(H=1.54 m);D为拉索直径(D=0.12 m);ρ为空气密度;U为来流风速。
能量的积分采用梯形公式进行计算,平均单个周期内气动力对下游拉索输入的总能量E=ED+EL。由于拉索自身阻尼比很小,约为0.001,对尾流驰振的抑制作用很小,故在不考虑拉索阻尼的条件下偏安全地认为,如果E>0,则表明气动力对拉索做正功,拉索在运动中吸收能量,其振动状态能够保持,且振幅有增大趋势;反之如果E<0,则表明拉索运动中消耗能量,拉索现有振动状态不能维持,振幅会逐渐衰减。
2 强迫振动风洞试验
通过强迫振动风洞试验,模拟了并列拉索尾流驰振现象,从气动力做功的角度对尾流驰振特性及其机理进行了研究,探讨了不同运动轨迹、振幅、频率以及来流风速对尾流驰振性能的影响。
2.1 试验装置
试验在湖南大学HD-2风洞边界层高速试验段进行,采用湖南大学风工程试验研究中心自主研发的3自由度强迫振动装置。振动均由全数控伺服电机驱动,各自由度方向振动的初始相位连续可调,范围为0°~360°,频率范围为0~3 Hz,最小频率间隔为0.01 Hz;振幅范围为0~24 mm,隔4 mm分级可调,并可实现侧向、竖向和扭转方向的7种相互耦合运动,试验装置传动方案和驱动原理如图1和图2所示[16]。
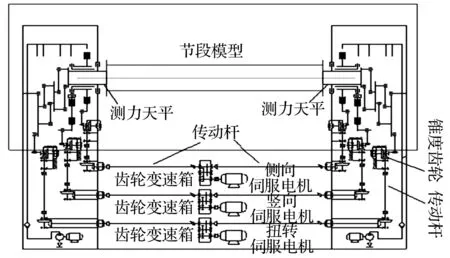
图1 机械传动原理图Fig.1 Scheme of mechanical transmission system
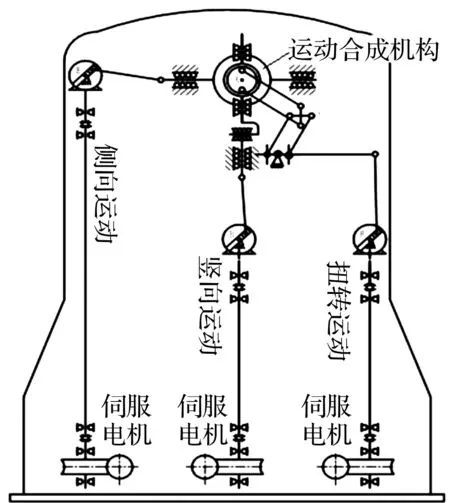
图2 机械驱动系统工作原理图Fig.2 Scheme of working principle of mechanical drive system
试验时节段模型通过两端的五分量杆式测力天平与驱动装置固结,运动时模型与天平同步,本文采用竖向和侧向两自由度耦合振动来模拟尾流驰振现象,模型两端各布置一个竖向和侧向位移计,通过东华采集系统对模型的位移与受力进行同步记录,采集时长为60 s。试验中发现下游拉索运动的惯性力远小于作用其上的气动力,且惯性力做功为0,故测力天平所得结果可直接视为气动力大小。试验中阻力与水平方向位移均以来流方向为正,升力与竖向位移均以向上为正。试验装置如图3所示。

图3 安装在风洞中的并列拉索模型Fig.3 Parallel cable models in wind tunnel
2.2 运动轨迹
尾流驰振发生的本质在于尾流中存在压力(速度)梯度,使得振动结构能够从来流中吸收能量,使其振幅不断增加,振动轨迹也不断改变。由于尾流驰振初始阶段的振幅较小,通常可将其轨迹分解为沿x和y方向的简谐振动,以及以原静止点为中心沿顺时针或逆时针(调节180°相位差得到)方向的椭圆运动(见图4)。在风速U=20 m/s时,单根拉索对应雷诺数为1.3×105,相应的斯托罗哈数约为0.2,得到拉索漩涡脱落频率为33.3 Hz。考虑到竖向和侧向振动频率应远小于拉索漩涡脱落频率,试验中基于实际工程背景取为0.46 Hz,拉索起振时,为振幅较小的椭圆轨迹,因此基于工程背景中已完成的并列拉索气弹模型尾流驰振试验结果,取水平振幅Ax=24 mm(即0.2D)、竖向振幅Ay=8 mm,得到并列拉索在水平间距比L/D=4.3、竖向间距比T/D=±1(即±15°攻角附近)以及单个圆柱工况,4种不同运动状态下气动力输入的总能量E如表1所示,下游拉索运动轨迹如图5所示。
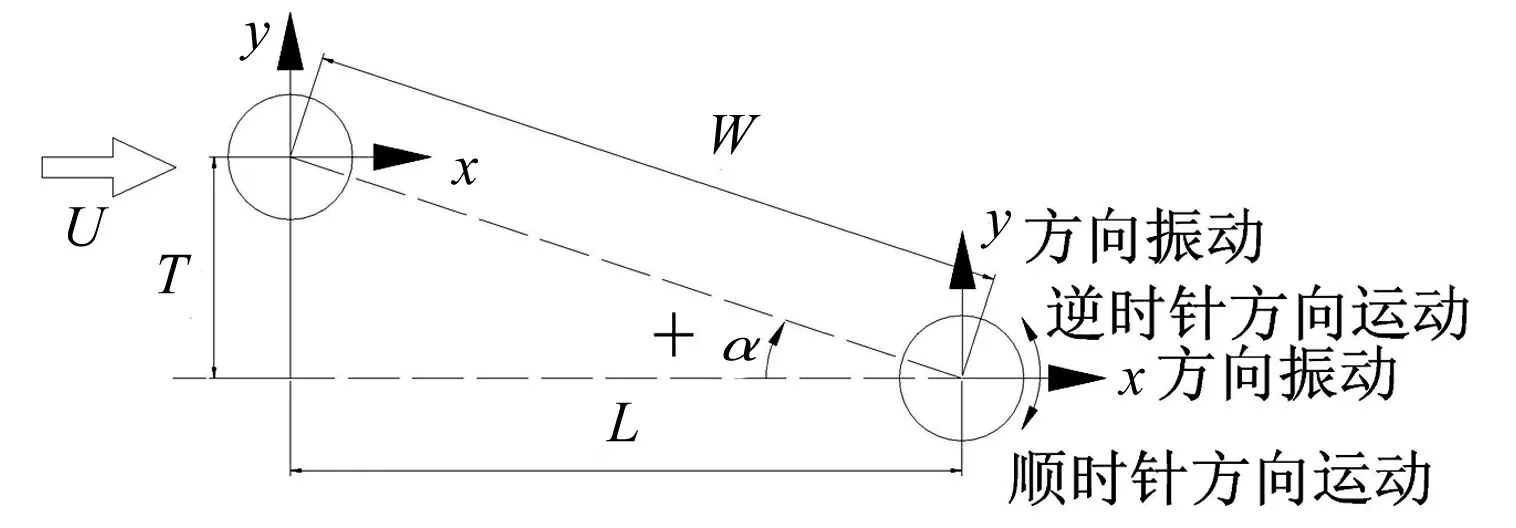
图4 振动方向示意图Fig.4 Schematic diagram of vibrating direction
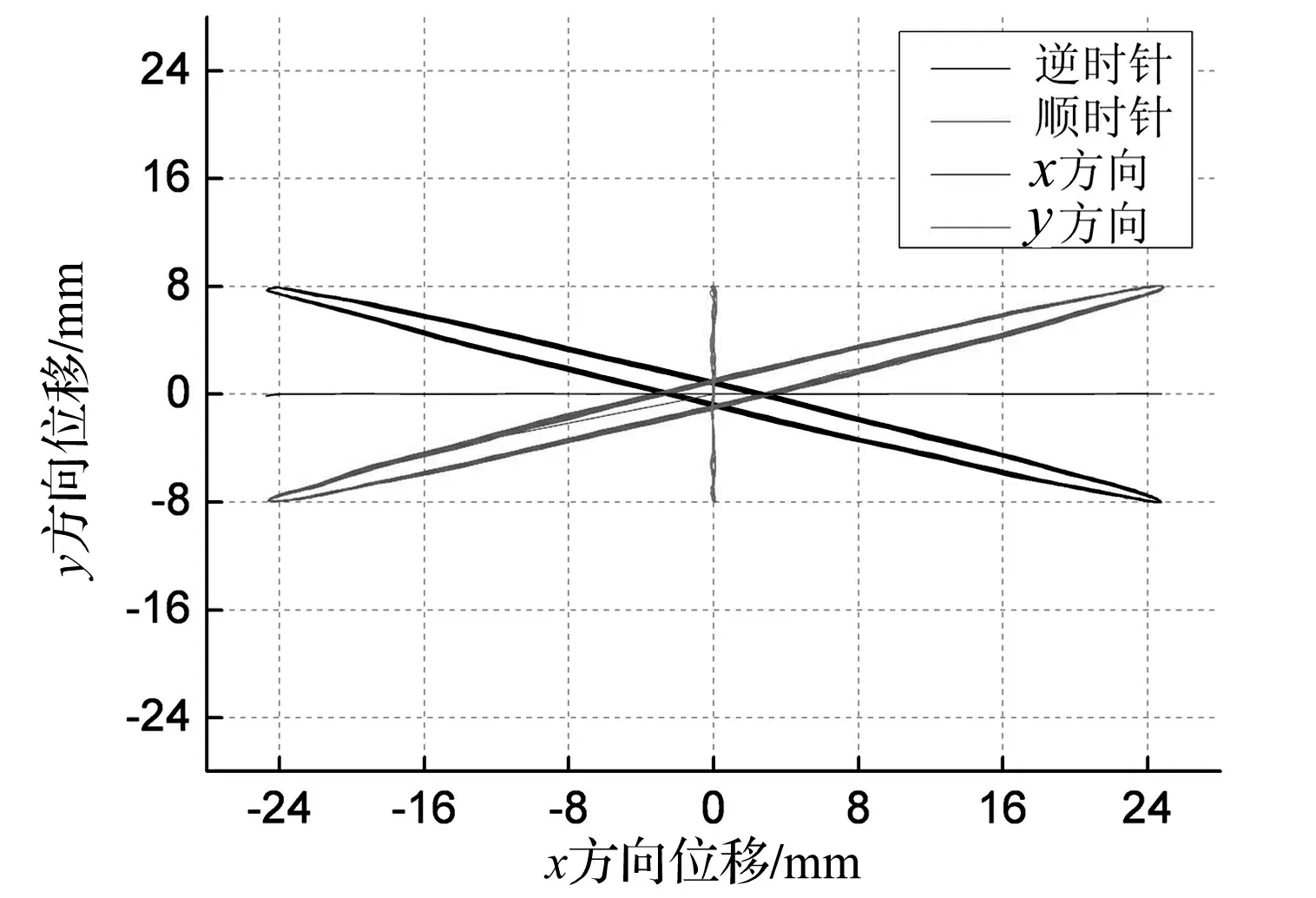
图5 不同运动方向下的振动轨迹Fig.5 Vibration orbits in different directions
由表1可知,当L/D=4.3时,拉索单独沿x或单独沿y方向作简谐振动时,气动力输入的总能量E<0,拉索不能维持该方向的运动;仅当下游拉索位于尾流中心线下方(即所处攻角为正)并沿逆时针方向做椭圆运动或位于尾流中心线上方(即所处攻角为负)且沿顺时针方向做椭圆运动时,气动力输入的总能量E>0,拉索能够维持在该方向上的运动,即尾流驰振可能发生。而单圆柱无论朝哪个方向运动,均无能量输入。
以上研究表明,尾流驰振具有明确的方向性。当下游拉索处于尾流外侧时,沿来流方向运动;当其处于尾流中心时,沿逆流方向运动。这可从拉索所受阻力大小来解释,当下游拉索靠近尾流外侧时,上游拉索的遮挡效应减小,下游拉索所受阻力较大,运动与来流方向一致;当其靠近尾流中心时,由于遮挡效应增大,所受阻力较小,运动方向与来流方向相反[17]。分析结果与已有结论一致。

表1 不同振动轨迹时气动力输入的总能量
2.3 尾流驰振不稳定区域
并列拉索是否发生尾流驰振与两索之间的相对位置密切相关,试验中分别取水平间距L/D=2、4.3、6、8;取竖向间距T/D=0~4,间隔为0.5D,依据上节分析结果,迫使下游拉索做逆时针方向的椭圆运动,侧向和竖向振幅保持不变,振动频率为0.46 Hz,来流风速为20 m/s,得到不同位置下气动力对下游拉索平均单个周期内输入的能量如图6所示。
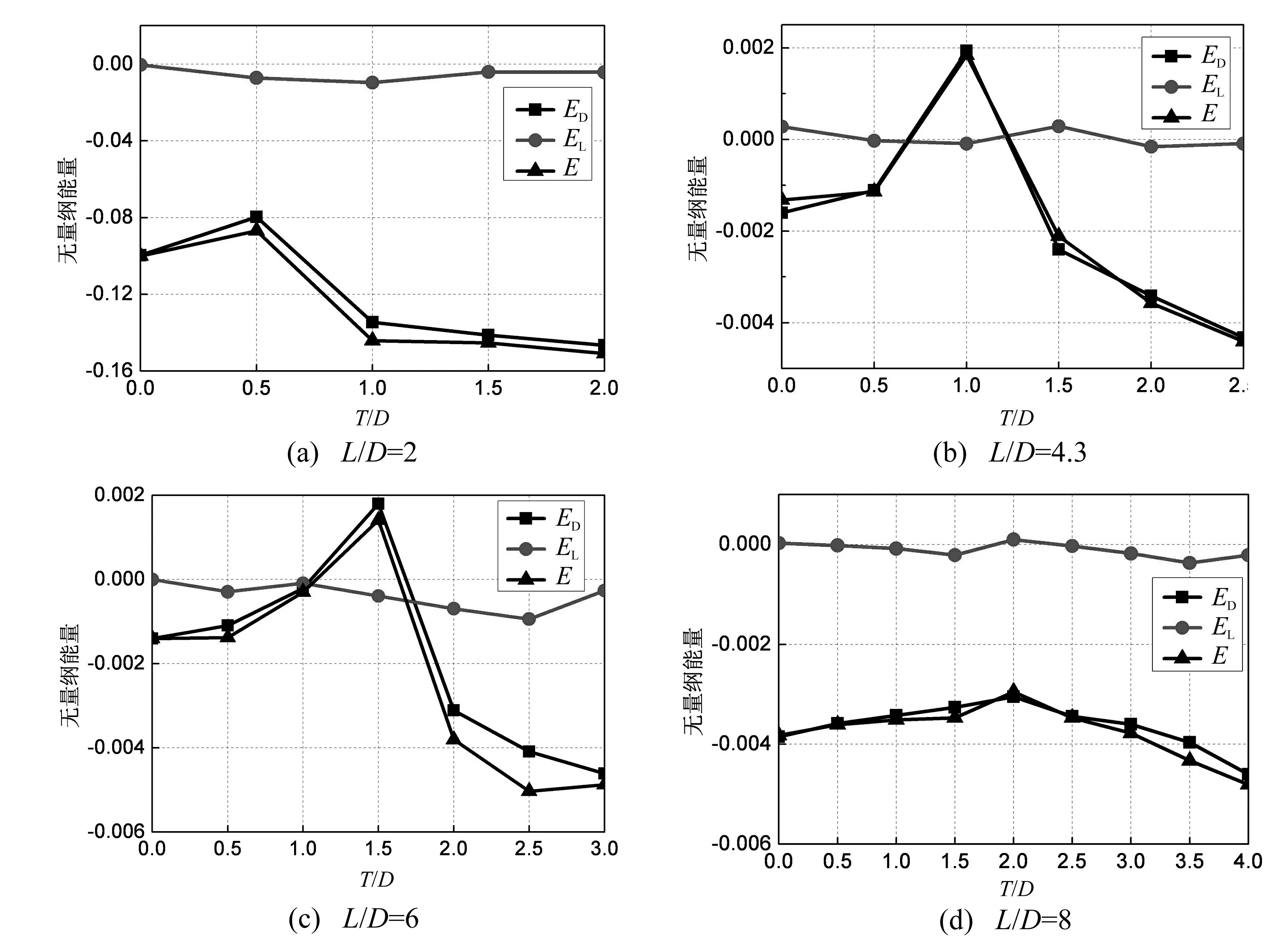
图6 不同位置下气动力输入的能量Fig.6 Input energy of aerodynamic forces at different positions
由图6可知,仅当L/D=4.3、T/D=1与L/D=6、T/D=1.5时,气动力输入的总能量E>0,下游拉索可能发生尾流驰振,而其他位置均能保持稳定。阻力做功ED与气动力输入的总能量E具有相同的变化规律,而升力做功EL很小,且基本为负值,表明拉索在尾流驰振过程中,阻力为其不断输入能量,而升力则表现为抑制作用,所得结果与基于能量分析方法的数值模拟结果一致。
当L/D不变,随着T/D增加(即风攻角增加),对应的总能量E呈现出先增加后减小的趋势,表明当两索中心的连线与来流在一定的攻角范围内时,尾流驰振才可能发生,这与已有的气弹模型试验及数值模拟结果相吻合。
3 尾流驰振机理研究
上节通过对尾流驰振特性的研究,验证了能量分析方法的可靠性,因此本节主要利用该方法对尾流驰振的机理展开研究,并与已有的数值模拟结果进行对比。下游拉索的椭圆运动轨迹可以分解为沿x和y方向简谐振动的叠加,即拉索尾流驰振可以分解为沿x方向和沿y方向单个自由度的驰振,而气动力则直接通过测力天平得到,因此当拉索沿某一方向运动时,气动力输入的能量只与这一方向上所受的力有关。
3.1 沿x方向的振动
基于第2.3节的计算结果,以并列拉索相对位置L/D=6.0,T/D=0~3.0的部分工况为例,从阻力对下游拉索做功的角度对尾流驰振机理进行了分析,得到10 s内各工况下拉索水平方向截面位移与阻力做功时程曲线如图7所示。
由图7可知,当T/D=0时,前柱对后柱的阻挡效应最大,阻力及其做功波动幅值最小;随着竖向间距比T/D增加,前柱的阻挡效应减少,后柱所受阻力增加,其做功波动幅值也相应增加;当T/D=3时,已与单圆柱工况接近。因此,阻力大小能够在很大程度上反映其做功波动幅度的大小。此外,阻力做功时程曲线与其截面位移时程曲线一样,存在明显一致的正负部分,且两者相位差几乎为90°,表明尾流驰振发生的条件在于:单个周期内阻力对下游拉索沿来流方向运动做的正功要大于其沿逆流方向运动做负功的绝对值。如果将阻力做功时程曲线看作准简谐曲线,则发生尾流驰振时阻力沿来流方向做正功部分对应的阻力略大,而沿逆流方向做功部分对应的阻力略小,即下游拉索发生尾流驰振时,沿来流方向的阻力要略大于沿逆流方向的阻力,阻力才会对拉索输入能量。
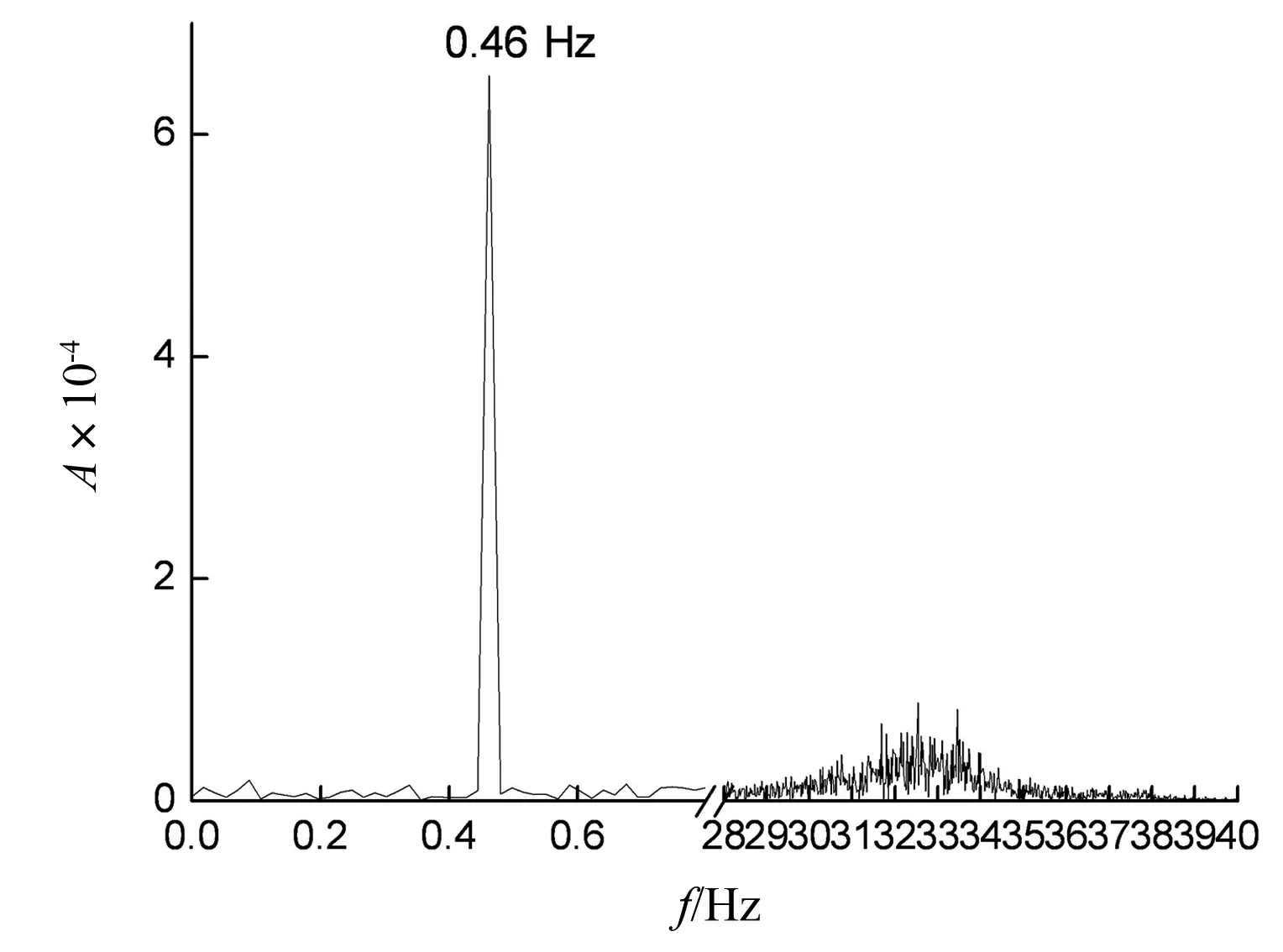
由图7还可知,当T/D=0时,阻力做功时程曲线相对光滑;当1≤T/D≤2时,两圆柱之间的气动干扰特性略为明显;当T/D=3及单圆柱工况(可看做两圆柱中心间距为无穷远)时,由于下游圆柱基本远离尾流区域,阻力做功时程曲线变得相对光滑,但所有阻力做功时程曲线均包含有2个频率成分,高频部分由上游拉索和下游拉索自身漩涡脱落产生(涡脱频率为33.3 Hz),该成分对阻力做功的平均值影响较小,可忽略不计,这也从侧面反映了尾流驰振主要由准定常力所控制,而低频部分由下游拉索自身振动产生,其频谱如图8所示。
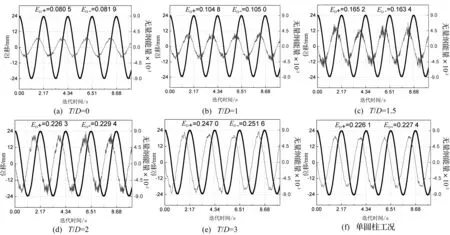
图7 截面位移与阻力做功时程曲线Fig.7 Displacement curves of cross-section and time-history curves of work done by drag
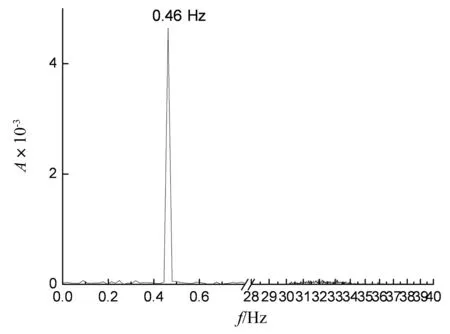
图8 阻力做功频谱图Fig.8 The frequency spectrum of work done by drag
如果将拉索平均单个周期内阻力做功ED分为正、负两个部分,取其绝对值用ED+和ED-表示,即ED+为阻力平均单个周期内对下游拉索做正功的总和,ED-为阻力平均单个周期内对下游拉索做负功总和的绝对值(见图7),则由于阻力大小能够在很大程度上反映其做功的大小,故下游拉索向右和向左运动速度达到最大时对应阻力FD+和FD-的大小关系能够较好的反应其运动过程中阻力平均值的大小关系,即ED+和ED-的关系。
当T/D=0时,FD+=FD-,因此ED+与ED-较为接近,但ED-略大于ED+,这主要是由下游拉索的运动速度造成的。当下游拉索向左和向右运动过程中,对应阻力均值是相等的,但在来流存在时,尽管下游拉索运动最大速度相比来流风速很小,依据相对运动理论,拉索向左运动所受阻力要大于向右运动的阻力,使得拉索阻力对其做的负功ED-要略大于正功ED+;随着T/D增加,FD+也增加,FD-却呈现先减小后增大的趋势,使得T/D=1时ED+ 综上所述,只有当下游拉索沿来流方向运动受到的阻力大于其沿逆流方向运动的阻力时,阻力才会对其输入能量,这与单自由度准定常驰振理论中升力系数斜率为负的结论类似。 3.2 沿y方向的振动 分析升力对下游拉索做功时,则只考虑下游拉索沿升力方向的运动。与研究阻力方向振动机理一样,以并列拉索相对位置L/D=6、T/D=0~3部分工况为例,从升力做功的角度对尾流驰振机理进行了分析,得到10 s内各工况下拉索竖向截面位移与升力做功时程曲线如图9所示。 图9 截面位移与升力做功时程曲线Fig.9 Displacement curves of cross-section and time-history curves of work done by lift 由图9可知,与阻力做功时程曲线相比,升力做功时程曲线的高频成分波动更为明显,但波动幅值较阻力时程曲线要小很多。究其原因,上游拉索漩涡脱落及其自身漩涡脱落对升力的影响较阻力要大,导致升力做功时程曲线高频成分波动更为明显,但由于升力相对较小,使得其做功时程曲线的幅值较小,升力做功时程曲线对应频谱如图10所示。 下游拉索在尾流失稳区域以外所受升力平均值几乎为0,升力做功曲线并无正负部分,且升力做的正功均略小于负功的绝对值,这是由于竖向风速平均值在水平和竖直方向变化很小,可认为下游拉索受到的升力不随两索相对位置而发生变化,因此下游拉索在椭圆周期内的平均升力相等且近乎为0。 由图9还可知,与阻力做功不同的是,尽管升力做功曲线在尾流失稳区域以外没有明显的正负部分,而是以能量为0的中心线上下波动,但在尾流干扰最为显著的T/D=1.5处(此处为失稳区域),升力做功时程曲线从整体上仍存在正负部分的趋势,且其做功时程曲线与其截面位移时程曲线的相位差也接近于90°,这表明尾流驰振过程中,下游拉索在整个周期内所受升力方向总体上为正,即当拉索沿升力方向(即逆流方向)运动时升力对其输入能量,而沿反方向(即来流方向)运动时则消耗能量,故在单个周期内升力做功接近于0。结合阻力做功时程曲线可知,尾流驰振过程中阻力与升力在尾流驰振过程中做功总是相反的,这表明当拉索沿来流方向运动时,阻力做正功,而升力做负功;当其沿逆流方向运动时,阻力对下游拉索做负功,升力却对其做正功。由于升力相比阻力较小,可认为升力对阻力做功存在一定程度的抵抗效应,但其影响较小,且单个周期内升力做的正功与负功的绝对值基本相等,这是由于拉索沿来流方向运动时受到的升力与沿逆流方向的升力十分接近所致。 图10 升力做功频谱图Fig.10 The frequency spectrum of work done by lift 综上所述,尾流驰振过程中,当拉索沿来流方向运动时,阻力做正功,而升力做负功;当其沿逆流方向运动时,阻力做负功,升力则做正功,升力做功对阻力做功存在一定的抵抗效应。如果从拉索单个运动周期内气动力输入能量的角度来说,阻力对拉索输入能量,而升力则耗散能量,且阻力输入的能量要远大于升力耗散的能量。 由于影响尾流驰振的因素有并列拉索的相对位置、振幅、来流风速及振动频率,因此在研究并列拉索相对位置以及尾流驰振机理的基础上,对影响尾流驰振性能的因素进行了参数化研究。 4.1 振幅的影响 由于以上尾流驰振的振幅均是基于水平振幅Ax=24 mm,竖向振幅Ay=8 mm,得到升力做功很小的结论,这有可能是竖向振幅比横向振幅小所致,为了排除这一因素,使下游拉索在位置L/D=4.3、T/D=1以相同频率(0.46 Hz)和来流风速(20 m·s-1)下做以坐标原点为中心的圆周运动,其振幅分别为8 mm,16 mm,24 mm,得到气动力对下游拉索单个周期内运动所做的功,其计算结果如图11所示。 图11 不同圆周半径时输入的能量Fig.11 Total input energy in different radii 由图11可知,随着圆周运动幅值的增大,气动力输入的能量也随之增加。在运动过程中,阻力对下游拉索做正功,使得其在阻力方向的振动有增大趋势;而升力对下游拉索做负功,使得其在升力方向的振动被抑制。在竖向和侧向振幅相同的情况下,阻力做功仍远大于升力做功,表明升力做功比阻力做功小并非其振幅小所致,恰恰是因为下游拉索在竖直方向的运动被抑制,而在水平方向的运动得到加强,才导致其运动轨迹由圆周运动变为椭圆轨道,且其振动主轴靠近阻力方向,这与已有研究成果是一致的。 4.2 来流风速的影响 为研究来流风速对尾流驰振性能的影响,取四个不同位置L/D=2、T/D=0.5;L/D=4.3、T/D=1;L/D=6、T/D=1.5;L/D=8、T/D=2,来流风速18~22 m/s,间隔2 m/s,水平振幅Ax=24 mm,竖向振幅Ay=8 mm,频率0.46 Hz,得到气动力对下游拉索平均单个周期内做椭圆运动所输入的总能量如图12所示。 由图12可知,当两拉索位置一定时,风速越大,气动力输入的总能量E也越大;当下游拉索处于L/D=2.0、T/D=0.5位置时,气动力对其做的负功明显大于其他位置,这可以从正反两个方面进行解释:由于两索相距较近,下游拉索的振动对流场干扰也最强烈,甚至能够破坏尾流场,进而避免尾流驰振的发生。反过来说,当两索相距较近,来流经过静止双圆柱时,双圆柱类似于单个物体结构,从而表现为单个钝体的气动特性,两圆柱之间不能形成漩涡,使得下游拉索能够保持良好的稳定性。 图12 不同来流风速时输入的总能量Fig.12 Total input energy in different wind velocities 4.3 振动频率的影响 为研究振动频率对尾流驰振性能的影响,取风速为20 m/s,频率范围0.46~2 Hz,其他试验条件与4.2节相同,得到气动力对下游拉索单个周期内做椭圆运动所输入的总能量如图13所示。 图13 不同频率时输入的总能量Fig.13 Total input energy in different frequencies 由图13可知,椭圆运动频率越高,气动力输入的总能量越低,在L/D=4.3和L/D=6工况下,当拉索振动频率大于或等于1 Hz时,其总能量E<0,气动力对下游拉索输入能量为负,拉索不具备尾流驰振发生的条件。究其原因,拉索频率增大,相应的运动速度会增加,由3.1节可知,下游拉索发生尾流驰振的条件在于:沿来流方向运动时,阻力做的正功ED+要大于逆流方向运动时阻力做负功的绝对值ED-。因此,随着下游拉索振动速度的增加,会使得ED+减小而ED-增加,当ED+ 本文采用强迫振动装置重现了尾流驰振现象,基于能量判断方法,对拉索节段模型进行了尾流驰振风洞试验研究,从气动力对下游拉索做功的角度,利用时域积分方法计算了阻力和升力对拉索输入的能量,研究了尾流驰振的运动轨迹、不稳定区域及其振动机理,分析了下游拉索不同振幅、来流风速以及频率对尾流驰振性能的影响。通过以上研究得到以下结论: (1)并列拉索尾流驰振与其相对位置密切相关,当两索中心间距确定且其连线与来流方向的风攻角处于一定范围内时,尾流驰振才可能发生,且尾流驰振具有明确的方向性。 (2)尾流驰振发生过程中,阻力对拉索做正功,使得其在该方向上的振动加剧;而升力做功很小,且基本为负,表现为抑制下游拉索在竖直方向的振动。 (3) 尾流驰振发生时,与阻力做功相比,升力做功表现出一定的抵抗效应,两者做功时程曲线与其截面位移时程曲线一样存在明显一致的正负部分,两者相位差几乎均为90°。 [ 1 ] 陈政清. 桥梁风工程[M]. 北京:人民交通出版社,2005:1-8. [ 2 ] TANAKA H. Aerodynamics of cables[C]//Italy:5th International Symposium on Cable Dynamics, 2003: 11-21. [ 3 ] FUJINO Y, KIMURA K, TANAKA H. Wind resistant design of bridges in Japan:developments and practices[M]. New York: Springer-Verlag,2012:197-229. [ 4 ] LI H, LAIMA S, OU J P, et al. Investigation of vortex-induced vibration of a suspension bridge with two separated steel box girders based on field measurements [J].Engineering Structures, 2011,33(6): 1894-1907. [ 5 ] WARDLAW R L, COOPER K R, KO R G, et al. Wind tunnel and analytical investigations into the aeroelastic behavior of bundled conductors [J]. IEEE Transactions on Power Apparatus and Systems, 1975, 94(2): 642-654. [ 6 ] ZDRAVKOVICH M M. The effects of interference between circular cylinders in cross flow [J]. Journal of Fluids and Structures, 1987,1(2): 239-261. [ 7 ] TOKORO S, KOMATSU H, NAKASU M, et al. A study on wake-galloping employing full aeroelastic twin cable model [J]. Journal of Wind Engineering and Industrial Aerodynamics, 2000, 88(2): 247-261. [ 8 ] 陈政清,刘慕广,刘志文. 基于气弹模型的串列主缆气动干扰试验研究[J].振动与冲击,2008, 27(8): 7-11. CHEN Zhengqing, LIU Muguang, LIU Zhiwen. Experiment study on aerodynamic interference of tandem cables based on aeroelastic model [J]. Journal of Vibration and Shock, 2008, 27(8): 7-11. [ 9 ] 李永乐,王涛,廖海黎. 斜拉桥并列拉索尾流驰振风洞试验研究[J]. 工程力学,2010, 27(增刊1): 216-221. LI Yongle, WANG Tao, LIAO Haili. Investigation on wake galloping of parallel cables in cable-stayed bridge by wind tunnel test [J]. Engineering Mechanics, 2010, 27(Sup1): 216-221. [10] DIANA G,GIAPPINO S, MANENTI A, et al. A numerical approach to reproduce subspan oscillations and comparison with experimental data [J]. IEEE Transactions on Power Delivery, 2014, 29(3): 1311-1317. [11] DIANA G, BELLOLI M, GIAPPINO S, et al. Wind tunnel tests on two cylinders to measure subspan oscillation aerodynamic forces [J]. IEEE Transactions on Power Delivery, 2014, 29(3): 1273-1282. [12] 严波,蔡萌琦,吕欣,等. 四分裂导线尾流驰振数值模拟研究[J]. 振动与冲击,2015, 34(1): 182-189. YAN Bo, CAI Mengqi, LÜ Xin, et al. Numerical simulation on wake galloping of quad bundle conductor[J]. Journal of Vibration and Shock, 2015, 34(1): 182-189. [13] 黄伟峰,李勇,刘秋生,等. 桥梁吊杆索尾流驰振问题的数值研究[J]. 清华大学学报(自然科学版),2008, 48(11): 1931-1934. HUANG Weifeng, LI Yong, LIU Qiusheng, et al. Numerical investigation of wake galloping of suspension bridge cables [J]. Journal of Tsinghua University (Natural Science Edition), 2008, 48(11): 1931-1934. [14] 马如进,倪美娟. 中间索面斜拉桥并列拉索尾流驰振数值研究[J]. 振动与冲击,2013, 32(10): 91-94. MA Rujin, NI Meijuan. Numerical simulation on wake galloping of parallel cables of cable stayed bridge with central cable planes [J]. Journal of Vibration and Shock, 2013, 32(10): 91-94. [15] 唐浩俊,李永乐,廖海黎. 基于能量方法的塔周长吊索尾流驰振性能研究[J]. 中国公路学报,2014, 27(8): 42-52. TANG Haojun, LI Yongle, LIAO Haili. Research on wake galloping of long suspenders near bridge tower based on energy method [J]. China Journal of Highway and Transport, 2014, 27(8): 42-52. [16] 牛华伟,陈政清. 桥梁主梁断面18个颤振导数识别的三自由度强迫振动法[J]. 土木工程学报,2014, 47(4): 75-83. NIU Huawei, CHEN Zhengqing.Three degrees-of-freedom forced vibration method for identifying eighteen flutter derivations of bridge decks [J]. China Civil Engineering Journal, 2014, 47(4): 75-83. [17] SIMIU E, SCANLAN R H. Wind effects on structures: fundamentals and applications to design [M]. 3rd.ed. New York: Wiley-Interscience Publication, 1996: 1-323. Investigation on wake galloping of parallel cables by wind tunnel test based on an energy method WUQilin1,HUAXugang1,HUTengfei2 (1.Hunan Provincial Key Laboratory for Wind Engineering and Bridge Engineering, Hunan University, Changsha 410082, China; 2. Guangxi Academy of Communication Science,Nanning 530007, China) In order to study the wake galloping characteristics in a close spacing instability range, a series of wind tunnel tests based on an energy method were carried out. The imposed motion along quasi-elliptical orbits reproduced wake galloping phenomenon of a parallel cable by the forced vibration device. Based on the energy analysis method, the motion trajectory and the unstable region of the downstream cable was analyzed. And the mechanism of the wake galloping was studied from the work done by aerodynamic forces. The influence of amplitudes, velocities of wind flow and vibration frequencies on wake galloping of cables were further discussed. The investigation results show that the results with the energy method agree well with classical results and prove the reliability of the analysis method. parallel cables; wake galloping; energy analysis method; wind tunnel test; forced vibration 国家自然科学基金优秀青年基金资助项目(51422806);中国铁路总公司资助项目(MHHTZX [2013]0029-3) 2015-10-30 修改稿收到日期:2016-01-25 吴其林 男,硕士生,1992年7月生 华旭刚 男,博士,教授,1978年6月生 U443.38; U448.27 A 10.13465/j.cnki.jvs.2017.04.035
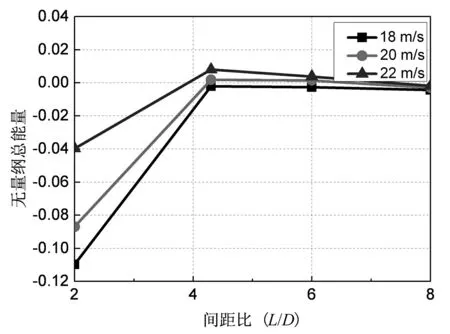
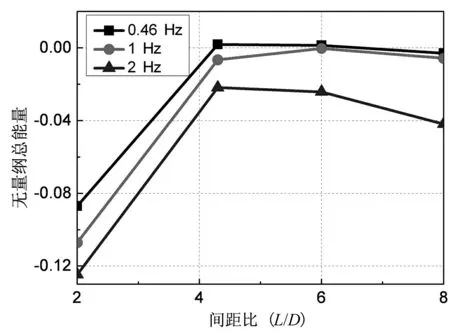
4 尾流驰振影响因素分析

5 结 论

