冲击载荷下双预置裂纹三点弯曲梁动态断裂实验

岳中文， 宋 耀， 邱 鹏， 胡庆文

(中国矿业大学 力学与建筑工程学院，北京 100083)

冲击载荷下双预置裂纹三点弯曲梁动态断裂实验

岳中文， 宋 耀， 邱 鹏， 胡庆文

(中国矿业大学 力学与建筑工程学院，北京 100083)

采用数字激光焦散线实验系统，对双预置裂纹三点弯曲梁进行了动态冲击实验，分析了双预置裂纹对试件裂纹尖端扩展速率和动态应力强度因子值的影响。实验结果表明：①双预置裂纹三点弯曲梁在动态冲击实验中，B裂纹作为开裂裂纹，其起裂时间和扩展速率峰值受到冲击载荷加载点与其预置位置之间水平距离值的影响，距离越小，起裂越快，扩展速率峰值越大；②试件开裂后，裂纹的裂纹扩展速度和动态应力强度因子值随时间的变化曲线均具有快速上升然后波动下降的规律；③B裂纹起裂所需能量随着A、B裂纹间距a值减小而增大。

双预置裂纹三点弯曲梁；焦散线；动态应力强度因子；断裂力学

许多实际工程(如道路与桥梁工程，混凝土浇筑工程等)中，构件内部往往会存在大量的微小裂纹，当构件表面受到外界动态载荷作用时，裂纹尖端附近的应力场会发生改变，产生应力集中现象，并会导致开裂。随着裂纹的扩展，各裂纹之间会产生相互影响作用，最终造成结构整体失稳，进而产生破坏。所以，针对多裂纹构件在动态载荷作用下，裂纹的扩展及他们间相互影响作用的研究具有十分重要的工程意义。

近年来，国内外多名学者均对含裂纹结构的力学特性进行了研究。KALTHOFF等[1]将裂纹动态扩展过程中的裂纹产生、扩展等行为引入焦散线理论，测定了冲击载荷下裂纹尖端应力强度因子及断裂韧性，并通过简化假设与数值运算，将速度调节因子加入静态应力强度因子以获取动态应力强度因子的方法。ROSAKIS[2]对应力强度因子的精度问题进行了深入研究，提出了混合型裂纹在快速传播时裂尖的焦散线方程。THEOCARIS等[3]通过研究裂纹尖端周围的应力分量表达式，得到了适用于常速扩展状态下，裂纹尖端焦散线的形状计算表达式。姚学锋等[4-5]采用动态焦散线实验方法，深入研究了含预制裂纹试件在动态三点弯曲冲击实验中裂纹尖端动态能量释放率的分布规律与含偏置裂纹三点弯曲动态断裂韧性，分析并讨论了裂纹扩展规律。陈爱军等[6]采用振动理论导出无裂纹梁内动态响应及分布，以权函数思想计算出含有预制裂纹的三点弯曲试件的应力强度因子K值，为求解含裂纹三点弯曲试件应力强度因子提出了新的方法。郑文炜[7]利用RFPA 3D软件模拟不同情况下含预置裂纹的大理石试件在三轴加载条件下的破坏行为特征，包括研究了侧压下，裂纹扩展机理以及三维多裂纹试件的开裂、扩展规律。杨仁树等[8]研究了含预置裂纹缺陷介质的动态断裂特性。岳中文等[9]针对具有倾角预制裂纹的三点弯曲梁，分析讨论了入射应力波、预制裂纹倾角与动态应力强度因子间的关系。BERGKVIST[10]研究了含预制裂纹试件的裂纹扩展速度与动态能量释放率之间的关系。ERDOGAN等[11]题出了动态能量释放率准则，并被广泛的用于动态断裂力学的研究中。

然而，目前针对含有多条预制裂纹的三点弯曲梁试件的裂尖应力强度因子及扩展规律的研究尚且很少，需要进一步进行实验分析与探讨。本文采用数字激光焦散线实验系统，研究了双预置裂纹三点弯曲梁的动态断裂特性，分析了双裂纹间在试件破坏过程中的相互影响作用因素。

1 实验原理

近年来，焦散线方法作为一种新的实验技术已经用于实验应力应变的分析中，并得到了广泛的认可。该方法可以通过简单且容易计算的几何图像得到可靠的富含信息的数据，由于该方法对应力梯度敏感，所以它适用于定量解决应力集中问题，是一种高效的研究裂纹尖端奇异应力场的方法。因此，焦散线方法在静动态断裂力学中具有广泛的应用。

焦散线方法利用纯几何光学的映射关系(见图1)，将应力集中区域的复杂变形状态转换为简单且清晰的阴影光学图形，进而确定有关力学参量。光线照射到结构受力的奇异区时，会在成像屏上产生相应的焦散斑(见图2)，通过测定其直径就可以确定裂纹尖端的应力强度信息。

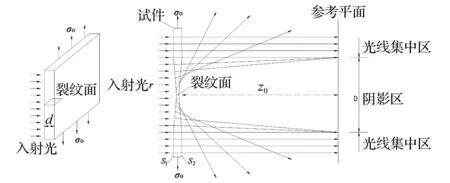
图1 焦散斑形成原理Fig.1 Principle of caustic spot formation

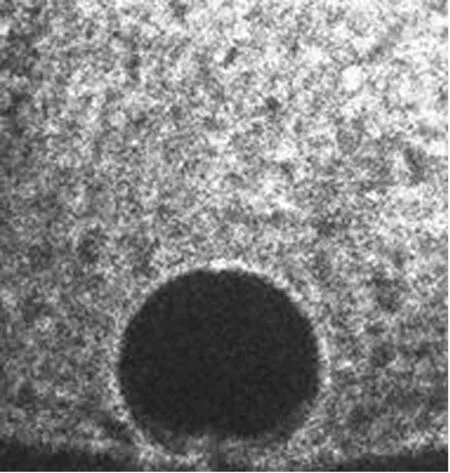
图2 焦散斑Fig.2 Caustic spot

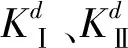
图3 数字激光动态焦散线系统光路图Fig.3 Schematic of the dynamic caustic experimental system

含双预置裂纹结构试件的动态三点弯冲击实验中，试件裂纹尖端在开裂前后可视为Ⅰ-Ⅱ混合型裂纹，其裂纹尖端焦散线如图4(a)所示，该种裂纹与纯Ⅰ型裂纹焦散线(见图4(b))的不同在于Ⅰ-Ⅱ复合型裂纹在形态上呈椭圆形，且KⅡ/KⅠ≠0。

图4 复合型与Ⅰ型裂纹尖端焦散线对比图Fig.4 Caustics comparisons graph of I type and mixed type crack

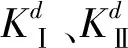
(1)

式中:c为试件的焦散应力光学常数；d为试件的有效厚度值；z0为试件距参考平面的距离，取z0=1 200 mm；μ为复合型裂纹尖端应力强度因子比值，可通过测得(Dmax-Dmin)/Dmax值来确定；g为焦散线的数值因子，由所得μ值确定，F(v)为裂纹扩展速度调节因子

(2)

式中，βi可以根据式(3)获得。

(3)

式中:c1和c2分别为PMMA中纵波速度和横波速度;v为裂纹扩展速度。根据已知理论可得[13]，当裂纹未起裂时，v=0 ,F(v)=1。当裂纹扩展时，F(v)恒小于1。本实验属低速冲击实验，裂纹扩展速率最大值约为515 m/s，故F(v)对实验结果影响较小。本文将F(v)取值为1。表1为PMMA试件的动态力学参数表。

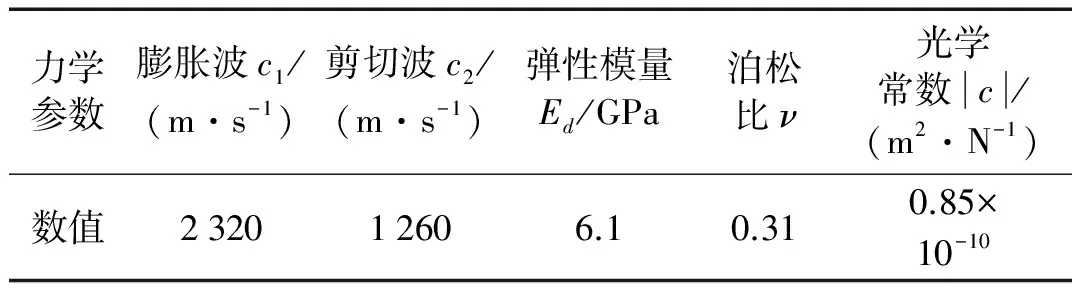
表1 PMMA试件的动态力学参数

2 实验设计

2.1 实验试件

本次实验所用试件材料为有机玻璃(PMMA)，尺寸为220 mm×50 mm×5 mm，如图5所示。两条预制裂纹设置于试件底部，并与之垂直，长度均为5 mm，宽度均控制在0.5 mm以内。按照两条预制裂纹相对位置将实验分为四组，取两条预置裂纹间距长度为a/mm，相关参数如表2所示。

图5 试件模型Fig.5 Model of specimen

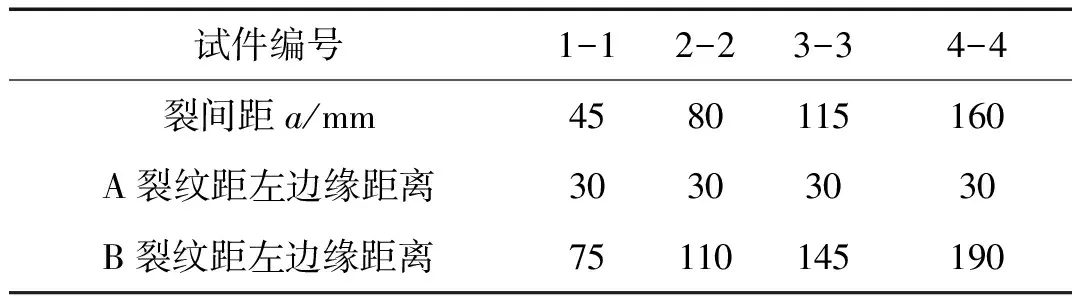
试件编号1-12-23-34-4裂间距a/mm4580115160A裂纹距左边缘距离30303030B裂纹距左边缘距离75110145190

2.2 动态焦散线三点冲击实验信息及操作步骤

图6 加载系统Fig.6 Loading system

3 实验结果及分析

3.1 裂纹扩展轨迹图

图7为实验后四组试件的裂纹扩展轨迹图。由图7可知，四组试件均由B裂纹作为主要裂纹开裂，裂纹扩展轨迹均呈现曲线状且最终均不同程度的向载荷加载点靠近。其中，1-1试件与3-3试件由于B裂纹距离试件加载点水平距离一致，所以该两组试件的裂纹扩展轨迹有一定的相似度，表现为裂纹扩展轨迹在扩展后期左右波动较明显。2-2试件B裂纹位置与加载点共线，所以其裂纹扩展轨迹近似呈直线状。4-4试件由于B裂纹位置距离试件加载点最远，所以其扩展轨迹的弯曲现象最明显。

3.2 动态焦散斑图

图8为四组试件在各时刻的动态焦散斑图片。由图8可知，当落锤冲击试件上表面时，B裂纹尖端附近的应力场发生改变，产生应力集中现象，裂尖不断积蓄起裂所需的能量，其尖端焦散斑尺寸不断变大；在B裂

纹起裂后的瞬间，其裂尖应力集中程度有所降低，焦散斑尺寸略微变小，随着裂纹的扩展，B裂纹裂尖焦散斑尺寸呈现波动变小的规律。A裂纹由于受到B裂纹开裂的影响，其裂尖应力集中程度始终较低，裂尖能量无法达到起裂所需能量最低值，故A裂纹在试件破坏过程中始终无法开裂。

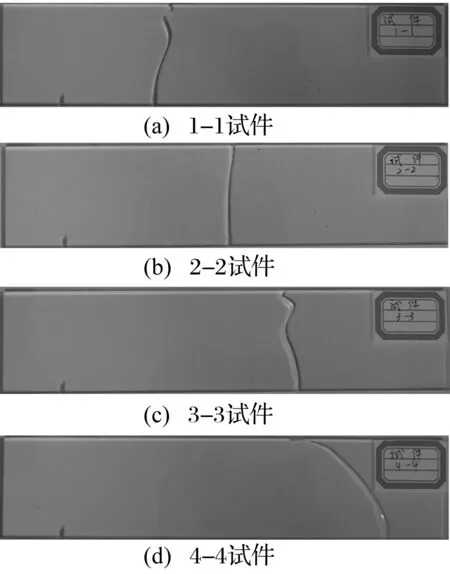
图7 裂纹扩展轨迹图Fig.7 Patterns of cracks

图8 各组试件裂纹尖端焦散斑图Fig.8 Dynamic caustic spots of specimens

3.3 裂纹扩展速率变化规律

通过测量焦散斑在各时刻的位置，确定焦散斑在单位时间间隔内的扩展长度，扩展长度与时间间隔的比值即为各时刻裂纹的扩展速率。本实验中，各组试件的A裂纹均未发生开裂扩展现象，故只针对B裂纹进行裂纹扩展速率的分析研究。图9为各组试件测得的B裂纹扩展速率随时间变化的曲线。

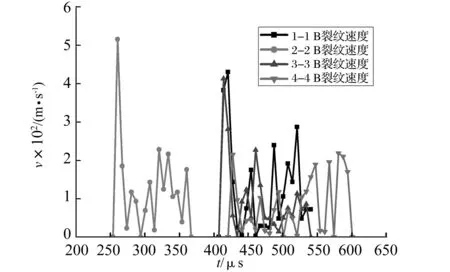
图9 B裂纹扩展速率变化曲线Fig.9 Velocity of B crack during propagation

由图9可得，当t=260.13 μs时，2-2试件B裂纹扩展速率达到最大值v=515 m/s； 1-1试件与3-3试件的起裂时间近似相等，均为t=406.87 μs，起裂后20 μs内，二者均达到各自扩展速率最大值(1-1试件为429.8 m/s，3-3试件为412.3 m/s)；4-4试件B裂纹于t=420.21 μs时起裂，并在t=433.55 μs时达到速率最大值v=214.39 m/s。四组试件的B裂纹扩展速率随时间变化曲线具有一定的相似性：均在裂纹扩展初期0～20 μs内达到速率最大值，然后快速降至最低点，最后在达到第二次速率峰值后振荡下降直至裂纹贯穿试件。该现象可以解释为：试件中B裂纹尖端在由落锤冲击产生的冲击波的影响和扰动下，不断积蓄能量供其开裂，当B裂纹起裂的一瞬间，裂尖能量得以快速释放，导致其扩展速率在极短的时间内达到最大值；随后由于裂尖应力集中程度的降低以及A裂纹裂尖破坏对B裂尖周边应力场的影响，B裂纹裂尖扩展速率急速下降至最小值；此后B裂纹尖端受到由冲击波在试件底部反射而形成的反射波与弯曲应力波的影响，产生了不稳定的动态响应，因此扩展速率产生了较大波动，并在达到第二次峰值后逐渐的振荡降低直至试件完全破坏。对比四组试件起裂时间可知2-2试件B裂纹裂尖起裂用时t最小(t0=246.79 μs)，这是因为2-2试件B裂纹位于冲击落锤所在直线上，即其裂纹预制位置与加载点间水平距离最近，所以裂尖能够更快速的达到其开裂所需能量的最低值并最快起裂。由于1-1试件与3-3试件中B裂纹与载荷加载点水平间距一致，所以该两组实验所得的B裂纹扩展速率与时间变化关系曲线具有一定的吻合性。此外，对比各组试件最大裂纹扩展速率值可知，B裂纹与试件加载点水平间距值越大，裂纹扩展速率所能达到的最大速率峰值则越低，反之，则越高。

3.4 裂纹尖端动态应力强度因子值变化规律

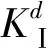
图10 B裂尖动态应力强度因子值随时间变化曲线Fig.10 Dynamic stess intensity fracture values of specimen’s B cracks

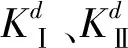
图11 A裂尖动态应力强度因子值随时间变化曲线Fig.11 Dynamic stess intensity fracture values of specimen’s A cracks

图12 A裂纹与B裂纹裂尖动态应力强度因子值随时间变化的对比曲线图Fig.12 Comparison of specimen’s A crack and B crack in

4 结 论

采用数字激光焦散线实验系统，借助透射式动态焦散线理论方法，对含双预置裂纹三点弯曲梁进行了动态冲击实验，所得结论如下：

(1)试件起裂的快慢和B裂纹扩展速率最大值均取决于B裂纹与载荷加载点间的相对水平距离，距离越小，则起裂越快，峰值越大；反之，则起裂越慢，峰值越小。

(2)试件在开裂后，A裂纹与B裂纹裂尖的动态焦散斑尺寸值、扩展速率速率与动态应力强度因子值随时间的变化曲线均具有快速上升、波动下降的特点，且波动的主要原因在于冲击波经试件底边反射形成的反射波和试件内部弯曲应力波对裂纹尖端的共同作用。

(3)A、B裂纹间距a值越小，则B裂纹起裂所需能量值与动态应力强度因子值越高。

[ 1 ] KALTHOFF J F, WINKLER S, BEINERT J. The influence of dynamic effects in impact testing[J]. International Journal of Fracture, 1977, 13(4): 528-531.

[ 2 ] ROSAKIS A J. Analysis of the optical method of caustics for dynamic crack propagation[J]. Engineering Fracture Mechanics, 1980, 13(2): 331-347.

[ 3 ] THEOCARIS P S, IOAKIMIDIS N I. The equations of caustics for crack and other dynamic plane elasticity problems[J]. Engineering Fracture Mechanics, 1979, 12(4): 613-615.

[ 4 ] 姚学锋, 方竞. 冲击载荷下扩展裂纹尖端动态能量释放率分布的焦散线分析[J]. 爆炸与冲击, 1996, 16(2): 111-116. YAO Xuefeng, FANG Jing. Analysis of caustics on dynamic energy release rate of running crack tip under impact load[J]. Explosion and Shock Waves, 1996, 16(2): 111-116.

[ 5 ] 姚学锋, 熊春阳, 方竞. 含偏置裂纹三点弯曲梁的动态断裂行为研究[J]. 力学学报, 1996, 28(6): 661-669. YAO Xuefeng, XIONG Chunyang, FANG Jing. Study of dynamic fracture behavior on three-point-bend beam with off-center edge-crack[J]. Acta Mechanica Sinica, 1996, 28(6): 661-669.

[ 6 ] 陈爱军, 曹俊俊. 带裂纹三点弯曲试样的动态应力强度因子分析[J]. 应用数学和力学, 2011, 32(2): 194-201. CHEN Aijun, CAO Junjun. Analysis of dynamic stress intensity factors of three-point bend specimen containing crack [J]. Applied Mathematics and Mechanics, 2011, 32(2): 194-201.

[ 7 ] 郑文炜. 含三维预置裂纹岩石破坏行为研究[D]. 北京：清华大学, 2011.

[ 8 ] 杨仁树, 王雁冰, 侯丽冬, 等. 冲击荷载下缺陷介质裂纹扩展的 DLDC 试验[J]. 岩石力学与工程学报, 2015, 33(10): 1971-1976. YANG Renshu, WANG Yanbing, HOU Lidong, et al. DLDC Experiment on crack propagation in defective medium under impact loading [J]. Chinese Journal of Rock Mechanics and Engineering, 2015, 33(10): 1971-1976.

[ 9 ] 岳中文, 杨仁树, 孙中辉, 等. 含倾斜边裂纹岩石冲击断裂模拟试验[J]. 煤炭学报, 2010, 35(9): 1456-1460. YUE Zhongwen, YANG Renshu, SUN Zhonghui, et al. Simulation experiment of rock fracture containing inclined edge crack under impact load [J]. Journal of China Coal Society, 2010, 35(9): 1456-1460.

[10] BERGKVIST H. The motion of a brittle crack[J]. Journal of the Mechanics and Physics of Solids, 1973, 21(4): 229-239.

[11] ERDOGAN F,SIH G C. On the crack extension in plates under plane loading and transverse shear[J]. Journal of Fluids Engineering, 1963, 85(4): 519-525.

[12] THEOCARIS P S, ANDRIANOPOULOS N P. Dynamic three-point bending of short beams studied by caustics[J]. International Journal of Solids and Structures, 1981, 17(7): 707-715.

[13] 岳中文, 王煦, 许鹏, 等. 含圆孔缺陷三点弯曲梁动态焦散实验[J]. 实验力学, 2015, 30(3): 339-347. YUE Zhongwen, WANG Xu, XU Peng, et al. Dynamic caustics experimental of three-point bending beam with circular hole defect [J]. Journal of Experimental Mechanics, 2015, 30(3): 339-347.

A dynamic fracture experiment of a three-point-bend beam containing double pre-existing cracks under impact load

YUEZhongwen,SONGYao,QIUPeng,HUQingwen

(School of Mechanics & Civil Engineering, China University of Mining &Technology, Beijing 100083, China)

A dynamic impact experiment of a three-point-bend beam containing double pre-existing cracks was performed by using a digital laser dynamic caustics experimental system, and the influence of double pre-existing cracks towards the specimen’s propagation velocity and the dynamic stress intensity factor (DSIF) was studied. The experimental results are: ① during the dynamic impact experiments, the initial cracking time and maximum propagation velocity value of B crack, which is the growing crack, decline as the horizontal distance away from loading point; ② after the cracking happens, curves of propagation velocity and DSIF along with time both follow the rules of increasing rapidly and declining with fluctuation; ③ the energy that B crack requires to initiate is enhanced as the distance between A and B cracks increases.

three-point-bend beam containing double pre-existing cracks; caustics; dynamic stress intensity factor; mechanics of fracture

国家自然科学基金面上项目(51374210)

2015-10-09 修改稿收到日期：2016-01-29

岳中文 男，博士，副教授，博士生导师，1975年生

宋耀 男，硕士，1991年生

O346.1

A

10.13465/j.cnki.jvs.2017.04.024