一类含有分数阶导数的参数激励振动问题

葛志新, 陈咸奖, 陈松林

(1.安徽工业大学 数理学院,安徽 马鞍山 243002; 2.安徽工业大学 商学院, 安徽 马鞍山 243002)

一类含有分数阶导数的参数激励振动问题

葛志新1, 陈咸奖2, 陈松林1

(1.安徽工业大学 数理学院,安徽 马鞍山 243002; 2.安徽工业大学 商学院, 安徽 马鞍山 243002)

研究了一类具有分数阶导数阻尼的参数激励振动问题。对含有由 Riemann-Liouville 定义的分数阶导数的Mathieu振动方程构造渐近解。利用多重尺度法,在激励参数取不同值的情况下,求得渐近解, 得到分数阶指数对解的影响。

多重尺度; 分数阶导数; 参数激励; 过渡曲线

振动现象是生活中常见的现象,也是学术界研究的热点话题,如NAYFEH[1]研究的自由振动、 非齐次项激励和参数激励下的各种受迫振动问题的渐近解及共振情况。刘灿昌等[2]研究的参数激励非线性振动时滞反馈最优化控制振动问题的稳定性等,他们研究问题的导数都用整数阶导数描述。随着数学的发展,分数阶导数逐渐进入学者们的视野,学者们发现分数阶导数更能准确描述记忆性材料的导数特性。学者们开始研究具有分数阶导 数阻尼的振动情况,如陈林聪等研究非齐次项激励的振动问题。学者们对用分数阶导数 描述外阻尼的参数激励的振动问题研究较少,且在文献[3-5]中使用谐波平衡法对分数阶阻尼Mathieu方程进行研究的。本文将在文献[6-15]的基础上研究含有参数激励的分数阶导数振动问题,对用分数阶导数来描述阻尼的Mathieu方程的解用多重尺度法求得渐近解,并研究分数阶导数对解的影响。

考虑

(1)

式中:δ为激励参数;0<ε≪1;0<α<1;n为>1的正整数。

1 第一种情况: 不接近于

引入多重尺度T0=t,T1=εt,则

(2)

(3)

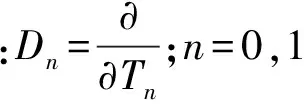
设

u(t)=u0(T0,T1)+εu1(T0,T1)+…

(4)

把式(2)～式(4)代入式(1)中,得

(δ+εcosnt)(u0(T0,T1)+εu1(T0,T1)+…)=0 (5)

令式 (5) 中ε同次幂相等, 得

所以,

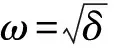
式中,cc为其前面项的共轭复数项,又

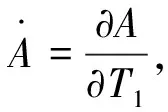
这里cosnt=cosnT0, 所以

(6)

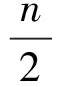
(7)

把式(7)化简, 得

(8)

把式(8)虚实部分开,并化简得

(9)

(10)

由式(9)和式(10)得当ω,α为定义域内常数时,ρ为指数性衰减, 运动是有界的,原问题的渐近解可表示为

ρe-i(θ+ωT0)+O(ε)=2ρcos(θ+ωt)+O(ε)

其中,

其中,C1,C2由初值决定,可以发现α对原问题的影响在振幅与频率上,振幅变化规律如图1所示, 且当α一定时,振幅指数性衰减。由此可以得到在一定的条件下u的变化曲线,如图2所示。

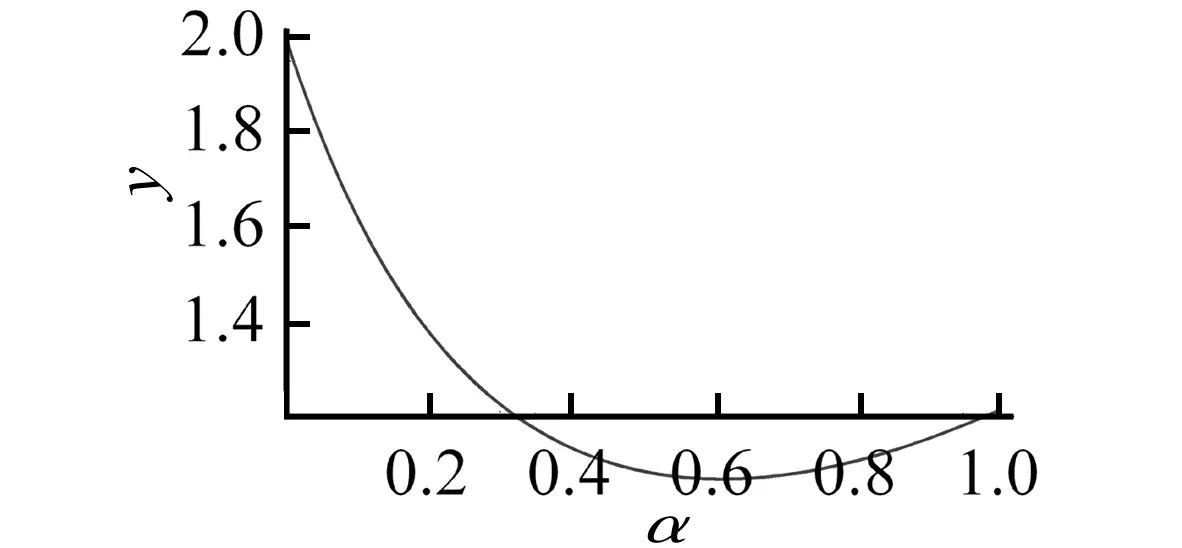
图,当ρ(0)=1时,y～α曲线,y为u(t) 的振幅Fig.θ(0)=0,ρ(0)=1,here y is the amplitude of the u(t)

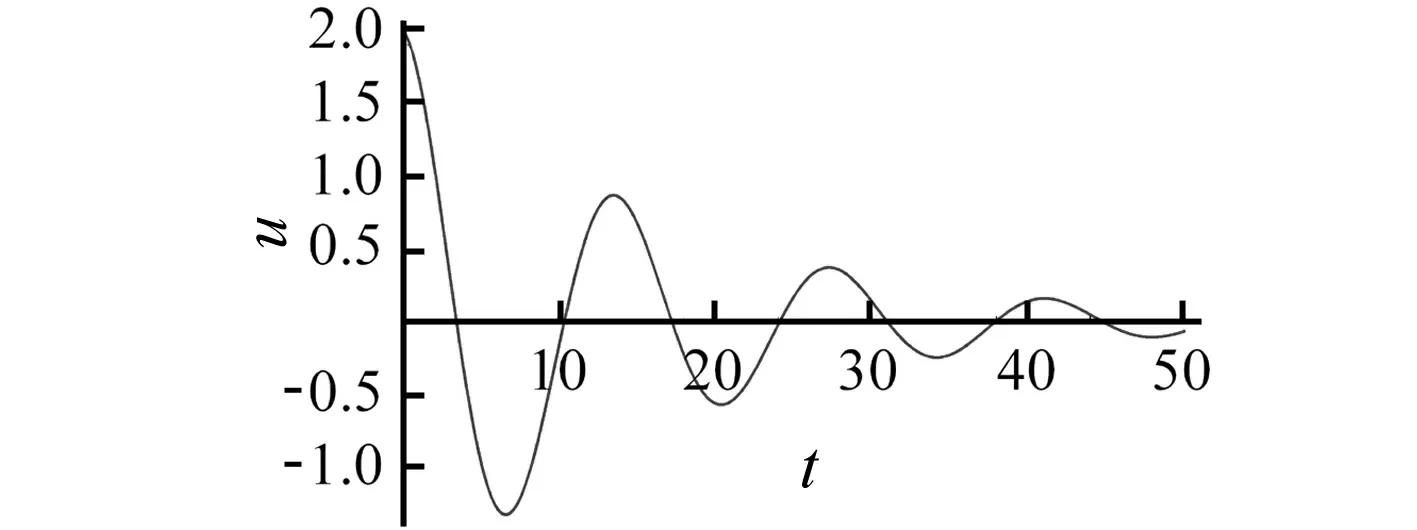
图2 当,ρ(0)=1时, u～t曲线Fig.,ε=0.1,θ(0)=0, ρ(0)=1

2 第二种情况

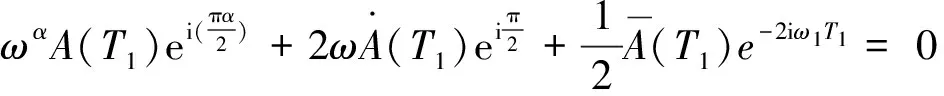
设A(T1)=ρeiθ,可以得到

化简得

(12)

把式(12)虚实部分开, 得

(13)

(14)

令χ=2θ+2ω1T1, 则式(13)和式(14)转化为

(15)

(16)

由式(15)和式(16)得

即

可以发现决定过渡曲线的表达式为

若ω≈1,则

因此,ω1随α的增大而增大, 如图3所示。

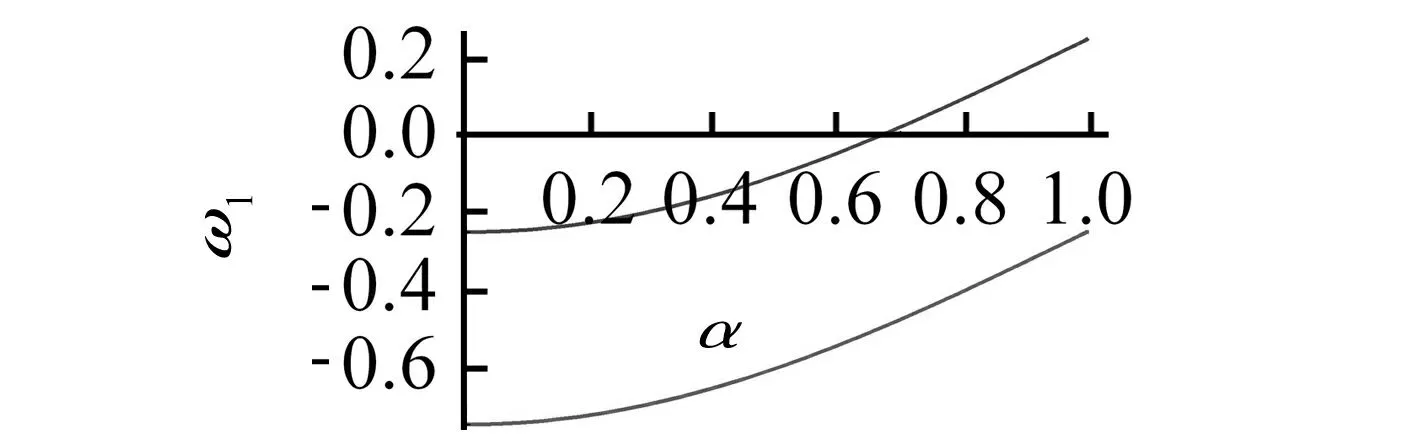
图3 曲线ω1～αFig.3 The curve is about ω1～α

所以过渡曲线为

α对过渡曲线的影响在ε项上,并且过渡曲线随着α的增大而向右移,如图4和图5所示。

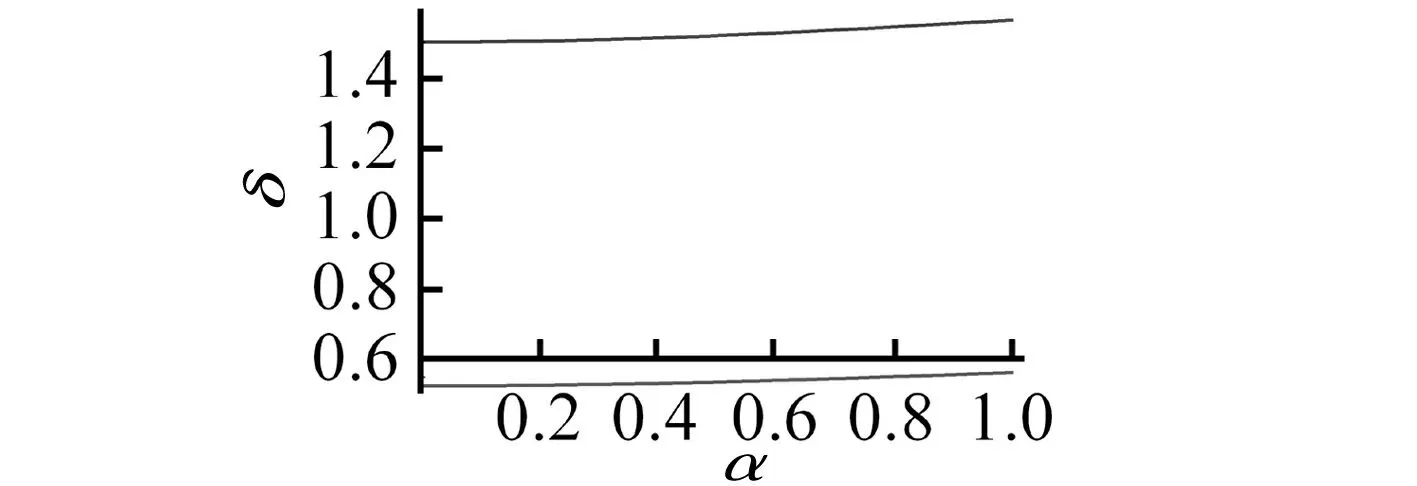
图4 当ε=0.1 时, δ～α曲线Fig.4 The curve is about δ～α as ε=0.1

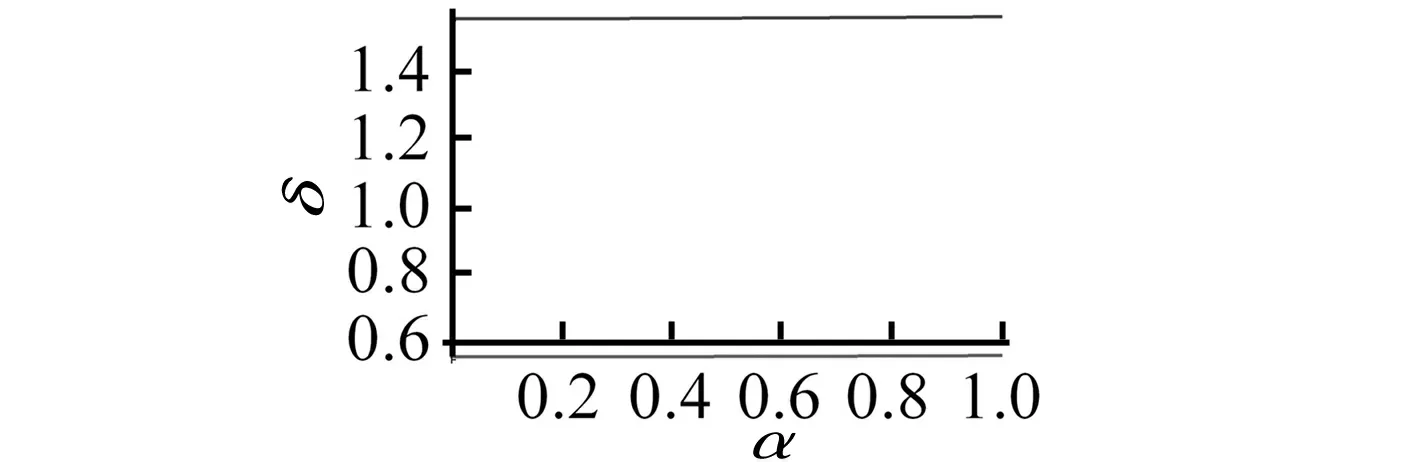
图5 当ε=0.01 时, δ～α曲线Fig.5 The curve is about δ～α as ε=0.01

为了研究渐近解,引入变换A=Be-iω1T1,并代入式(11), 得

(17)

令B=Br+iBi,则式(17)可转化为

(18)

(19)

寻找式(18)和式(19)中形如Br=breγ1T1,Bi=bieγ1T1的解。把Br=breγ1T1,Bi=bieγ1T1代入式(18)和式(19),得

(20)

(21)

求式(20)和式(21)的非零解。由式(20)和式(21)关于未知数br,bi的系数行列式为0, 得

从而

把式(22)代入式(20)得

即

(23)

把式(23)及变换A=Be-iω1T1,B=Br+iBi,Br=breγ1T1,Bi=bieγ1T1代入(4),得

u=(Br+iBi)ei(ωT0-ω1T1)+(Br-iBi)e-i(ωT0-ω1T1)+…

即

也就是

从而得到u的近似表达式, 即

(24)

其中,a1,a2由初始条件确定,由解可知α对解的影响在振幅上。令

(25)

ρ2=

(26)

(27)

ρ4=

(28)

可得到一定条件下α对ρi(i=1,2,3,4)的影响,如图6和图7所示。同时我们也能得到u的曲线图,如图8所示。

图6 εt=1，n=2，ω≈1，ω1=-cosπα22时，ρ1～α，ρ3～α曲线Fig．6Thecurvesareaboutρ1～α，ρ3～αasεt=1，n=2，ω≈1，ω1=-cosπα22图7 εt=1，n=2，ω≈1，ω1=-cosπα22时，ρ2～α，ρ4～α曲线Fig．7Thecurvesareaboutρ2～α，ρ4～αasεt=1，n=2，ω≈1，ω1=-cosπα22图8 ε=0．1，n=2，ω≈1，ω1=-cosπα22，α=12，u(0)=0．5，u′(0)=-0．5时，u(t)～t曲线Fig．8Thecurveisaboutu(t)～tasε=0．1，n=2，ω≈1，ω1=-cosπα22，α=12，u(0)=0．5，u′(0)=-0．5

3 结 论

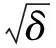
u(t)=2ρcos(θ+ωt)+O(ε)

(29)

其中,

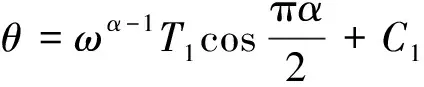
(30)

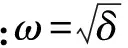
(31)

式中,a1,a2由初始条件决定,分数阶指数只对解的振幅有影响,振幅指数型增大。

2.1.5 镁。2012年全市叶片镁平均含量为2.93 g/kg(表1)，说明烟台市果园镁素严重不足。低土壤pH或高钾可能会造成叶片镁含量低。苹果收获前落果或果树枝条缺少花芽、细弱的结果短枝都与缺镁有关。施用含镁的石灰、颗粒镁或硫酸镁，以及叶片喷施六水硫酸镁都有较好的效果。

通过对含有分数阶导数的 Mathieu振动方程解析渐近解的研究,我们明确了该方程的振动规律包括周期、振幅、频率.这个研究为我们进一步研究含有分数阶导数的 Mathieu振动方程其他性质,如稳定性、极限环、分叉等提供了依据。参 考 文 献

[ 1 ] NAYFEH A H. Introduction to perturbation techniques[M]. Shanghai: Shanghai Translation Publishing House, 1990.

[ 2 ] 刘灿昌,岳书常,许英姿,等.参数激励非线性振动时滞反馈最优化控制[J]. 振动与冲击,2015,34(20):6-9. LIU Canchang, YUE Shuchang, XU Yingzi, et al. Optimal control of parametric excitated nonlinear vibration system with delayed linear and nonlinear feedback controllers[J]. Journal of Vibration and Shock,2015,34(20):6-9.

[ 3 ] RAND R H, SAH S M, SUCHORSKY M K. Fractional Mathieu equation[J]. Communications in Nonlinear and Science Numerical Simulation,2010, 15(11):3254-3262.

[ 4 ] LEUNG A Y T, GUO Z J, YANG H X. Transition curves and bifurcations of a class of fractional mathieu-type equations[J]. International Journal of Bifurcation and Chaos, 2012, 22(11):1853-1853.

[ 5 ] MESBAHI A,HAERI M,NAZARI M, et al. Fractional delayed damped Mathieu equation[J]. International Journal of Control, 2015,88(3):622-630.

[ 6 ] 陈林聪, 李海锋, 李钟慎,等.宽带噪声激励下含分数阶导数的Duffing-van del Pol振子的稳态响应[J].中国科学: 物理学力学天文学,2013, 43(5):670-677. CHEN Lincong, LI Haifeng, LI Zhongshen, et al. Stationary response of Duffing-van del Pol oscillator with fractional derivative under wide-band noise excitations[J]. Scientia Sinica Physica Mechanica & Astronomica, 2013, 43(5): 670-677.

[ 7 ] 杨建华, 刘厚广, 程刚. 一类五次方振子系统的叉形分叉及振动共振研究[J]. 物理学报, 2013,62(18): 180503. YANG Jianhua, LIU Houguang, CHENG Gang. The pitchfork bifurcation and vibrational resonance in a quintic oscillator[J]. Acta Physica Sinica,2013,62(18): 180503.

[ 8 ] 张路, 谢天婷, 罗懋康. 双频信号驱动含分数阶内、 外阻尼Duffing振子的振动共振[J]. 物理学报, 2014,63(1):68-74. ZHANG Lu, XIE Tianting, LUO Maokang.Vibrational resonance in a Duffing system with fractional-order external and intrinsic dampings driven by the two-frequency signals[J]. Acta Physica Sinica,2014,63(1):68-74.

[ 9 ] 韦鹏, 申永军, 杨绍普. 分数阶van der Pol振子的超谐共振[J]. 物理学报, 2014, 63(1):39-50. WEI Peng, SHEN Yongjun, YANG Shaopu. Super-harmonic resonance of fractional-order van der Pol oscillator[J]. Acta Physica Sinica, 2014, 63(1):39-50.

[10] 申永军, 杨绍普, 邢海军. 含分数阶微分的线性单自由度振子的动力学分析[J]. 物理学报,2012, 61(11):55-63. SHEN Yongjun, YANG Shaopu, XING Haijun. Dynamical analysis of linear single degree-of-freedom oscillator with fractional-order derivative[J].Acta Physica Sinica,2012, 61(11):55-63.

[11] 申永军, 杨绍普, 邢海军. 含分数阶微分的线性单自由度振子的动力学分析(Ⅱ)[J].物理学报,2012,61(15):61-69. SHEN Yongjun, YANG Shaopu, XING Haijun.Dynamical analysis of linear single degree-of-freedom oscillator with fractional-order derivative(Ⅱ)[J]. Acta Physica Sinica,2012,61(15):61-69.

[12] 莫嘉琪.非线性分数阶微分方程的奇摄动[J].应用数学学报,2006, 29(6):1086-1090. MO Jiaqi. Singular perturbation of nonlinear fractional differential equation[J]. Acta Mathematicae Applicatae Sinica,2006, 29(6):1086-1090.

[13] 葛志新,陈咸奖.一类含有两参数的小迟滞方程的渐近解[J].应用数学学报,2014,37(3):407-413. GE Zhixin,CHEN Xianjiang. The asymptotic solution of a class of small delay equations with two parameters[J].Acta Mathematicae Applicatae Sinica,2014,37(3):407-413.

[14] 葛志新. 一类二次奇摄动Robin问题[J]. 工程数学学报, 2011, 28(2): 245-250. GE Zhixin.A class of the quadratic singularly perturbed boundary value problems with the Robin condition[J]. Chinese Journal of Engineering Mathematics,2011, 28(2): 245-250.

[15] 葛志新.一类两参数奇异摄动拟线性微分方程组的边值问题渐近解[J].工程数学学报, 2013,30(4):611-618. GE Zhixin. Asymptotic solutions about a class of the quasilinear system of differential equations with two parameters and boundary value conditions[J]. Chinese Journal of Engineering Mathematics, 2013, 30(4): 611-618.

A class of parametric excitation vibration problems with fractional derivative

GEZhixin1,CHENXianjiang2,CHENSonglin1

(1.School of Mathematics & Physics, Anhui University of Technoloy, Ma’anshan 243002,China; 2.School of Economics, Anhui University of Technology, Ma’anshan 243002, China)

A class of parametric excitation vibration problems with fractional derivative damping was studied. First of all, the asymptotic solution of the Mathieu vibration equation of the fractional derivative defined by the Riemann-Liouville was structured. In the case of different values of excitation parameters, asymptotic solutions were obtained by the method of multiple scales. The influence of fractional order index on the asymptotic solution was obtained.

multiple scales; fractional derivative; parametric excitation; transition curve

安徽省高校自然科学研究重点项目(KJ2016A084)

2015-12-07 修改稿收到日期：2016-01-21

葛志新 女，硕士, 实验师，1970年10月生

陈咸奖 男，硕士, 副教授，1970年7月生 E-mail:chenxianjiang@sina.com

O175.14

A

10.13465/j.cnki.jvs.2017.04.014