高速转子分布式不平衡量无试重识别方法

章 云， 胡振邦， 梅雪松

(1.西安电子科技大学 机电工程学院，西安 710071； 2.西安交通大学 机械制造系统工程国家重点实验室，西安 710049)

高速转子分布式不平衡量无试重识别方法

章 云1， 胡振邦2， 梅雪松2

(1.西安电子科技大学 机电工程学院，西安 710071； 2.西安交通大学 机械制造系统工程国家重点实验室，西安 710049)

为有效抑制分布式不平衡量所导致的转子故障振动，提出一种高速转子分布式不平衡量识别方法，该求解方法无需试重，且振动测试过程可在低于临界转速下进行。通过扩展影响系数动平衡方法与转子动力学模型的比较分析，得出了动力学传递函数与影响系数之间的关联关系。基于有限元动力学模型结点，实现了分布式不平衡具体描述，通过增加振动测试转速的方式，实现了动力学传递函数矩阵的满秩，进而给出了分布式不平衡量的求解公式,并在转子动平衡实验平台上进行了实例验证。结果表明,按该方法识别的不平衡量进行配重校正后，转子临界转速前后残余振动比动平衡前降幅非常明显，验证了该方法所识别不平衡量的准确性。

高速转子；分布式不平衡；不平衡识别；无试重

旋转设备的振动状况是评估设备运行健康状态的重要参数。当转子处于高速旋转状态时，即使微弱不平衡量也会引起转子挠曲和内应力，导致转子剧烈振动，直接影响加工质量、甚至对转子自身组件造成破坏[1]。由于制造、安装误差以及材料的不均匀，转子不平衡故障必然存在。因此，如何控制转子不平衡振动是旋转机械使用过程中最为关键的问题之一[2]。

动平衡是典型的已知输出求解输入的逆问题，其实施过程中通常要进行多次启停车、试重，以获取转子影响系数、敏感因子等特性响应参数。然而，试重意味着自动化环节的中断，并且错误的试重更会使旋转机械运转状态急剧恶化。能否通过最少的试重次数实现转子的高效、平稳运行，是衡量现场动平衡方法的一个重要指标。如果试重选择得当，可以实现“试重即配重”的效果，无试重平衡方法[3-5]正是立足于这一思路而提出。

对于典型的质量呈集中分布的转子，如离心压缩机、发电机组、航空发动机转子等，其不平衡质量一般位于叶轮、风浆等特定的质量集中截面。然而，并非所有转子都属于这一类型，如机床主轴转子，其质量分布较为均匀，其不平衡状态假定为沿轴向呈连续空间分布更为合理。实质上，按照集中质量模型处理连续分布质量转子，可以识别出等效集中不平衡量[6]，并在当前转速下取得平衡效果，但若转速发生变化，此时仍用上一转速下识别的等效集中不平衡量为配重依据，将起不到良好的平衡效果。此外，无试重平衡方法通常需要运行在临界转速或临界转速附近获取振动模态信息，这给现场实施带来一定的风险。

为解决这一问题，通过有限元结点描述分布式不平衡量，并基于扩展影响系数动平衡方法与转子动力学模型，提出一种仅需在低于临界转速下采集不平衡振动数据的分布式不平衡量无试重识别方法，进而通过实验验证其有效性。

1 扩展影响系数动平衡方法

假设在K个校正面施加校正量抑制J个测振点的振动，则施加校正配重量之后，转子振动须要满足以下关系式[7]

Vj+TjkWk=0

(1)

式中:Tjk(j=1,2,…,J;k=1,2,…,K)为在第k个校正面施加单位校正量对第j个测点的影响系数；Vj为第j个测点的振动响应；Wk为第k个校正面所加校正质量。

式(1)中，若振动测点数J小于校正面数量K时，方程将有无穷解，需要增加式(1)的行数，使得影响系数矩阵满秩。为此，可增加平衡转速的数目，确保在各个转速下转子振动被抑制。假设平衡转速数为U，式(1)可扩展为

V+TW=0

(2)

式中:W={W1,W2,…,WK}T∈K为校正矢量序列;V={(VΩ1)T,(VΩ2)T,…,(VΩU)T}T∈JU为不平衡振动响应序列，VΩu∈J为Ωu(u=1,2,…,U)转速下振动响应序列；T={(TΩ1)T,(TΩ2)T,…,(TΩU)T}T∈JU×K，TΩu∈JK为Ωu转速下影响系数矩阵。

显然，只有当JU=K时，式(1)才有唯一解。

2 动力学传递函数与影响系数关联分析

对于具有N个结点，其间用N-1个轴段连接而成的转子系统，可分别对各单元进行分析，建立该单元结点力与结点位移间的关系[8]。当转子具有偏心的不平衡质量时，以结点位移为广义坐标的转子系统动力学微分方程式(3)所示

(3)

式中:Q={m1ε1eiα1,m2ε2eiα2, …,mNεNeiαN}T∈N为不平衡激励序列；δ∈N为不平衡响应；M∈N×N为质量矩阵；G∈N×N为陀螺效应矩阵；K∈N×N为刚度矩阵。

设不平衡响应特解为δ=AeiΩt，其中A={a1eiφ1,a2eiφ2, …,aNeiφN}T∈N，将之代入式(3)，并令B=Ω2[-Ω2M+Ω2G+K]-1，可得

(4)

为便于表述，设定式(4)中与第k个校正面、第j个测量面对应的有限元模型结点编号仍分别为k、j，若第k个结点的不平衡量为Qk，第j个结点的响应为Aj，则有

(5)

式中，ψkj(ω)为振动响应Aj(ω)落后于外部不平衡激励Qk(ω)的滞后角。

同理，若式(1)在第k个校正面有配重Wk，第j个测量面的响应为Vj，则有

(6)

式中:θkj为积分常数，它与转子初始条件相关;Πkj为鉴相点到不平衡位置角度。

式(5)与式(6)中，Aj和Vj都是振动响应；Wk是用于校正不平衡量的配重，其与不平衡激励Qk是反相关系；θkj、Πkj则与机械滞后角为ψkj有如下关系恒成立[9]

θkj-Πkj=-ψkj

(7)

由此，可以认为式(5)及式(6)右端等效，且两者幅值相等，相位相反。

3 基于动力学传递函数的分布式不平衡识别

为实现对连续分布式不平衡量的完整识别，需要对不平衡偏心曲线进行描述，学者们通过傅立叶级数展开[10]、高次多项式[11]等方式进行了尝试。实质上，如果识别的不平衡截面足够多，也能满足连续分布不平衡量的描述需要，在式(1)中，每个平衡校正面可视为一个不平衡量的识别面，即K足够大时，能够实现分布式不平衡的完整描述，但要使式(1)有解，需要增加测点J的数量，或者增加式(2)中平衡转速数U的数量。然而，在工程实际中测点布置及平衡转速都是有限制的，难以满足求解条件。

从式(7)可知，影响系数矩阵与动力学传递矩阵是等效的，由此，可以将扩展影响系数动平衡方法与动力学行为结合，将主轴转子的连续不平衡力等效到模型中的每个结点上，通过力学分析得出不同转速下振动与试重之间的关联关系，实现分布式不平衡量的完整求解。

通过式(3)可得

(8)

式中，IN∈N×N为单位对角矩阵。

在工业现场，受传感器布置条件的限制，仅能获得J个结点处的转子振动响应数据。为此，需增加平衡转速的数目U为N/J，使Q可解，则可将式(8)扩展及变形为

(9)

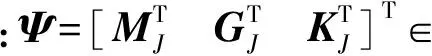
值得关注的是，尽管采用式(2)所表述的增加转速数量的方法，可以使得方程满秩，但由于其仅仅是简单的振动等效原理，所求解的不是真正物理位置上的不平衡量，按该公式进行动平衡也仅能保证测振点的振动被抑制。而通过式(9)所求解的是真正物理意义的不平衡量，平衡配重后转子各结点上的振动将被完全抑制，而不随转速等外部条件的改变而改变。

4 实例验证与分析

为验证不平衡识别方法的有效性，在转子实验平台上设计实验方案，平台设置两个振动测试点模拟工业现场测振布置，转轴上采用四个不平衡激励点模拟分布式不平衡，实验现场如图1所示。

图1 柔性转子动平衡实验现场Fig.1 Dynamic balancing experiment of flexible rotor

为体现不平衡分布差异性，分别采用直径为75 mm的钢、铝制质量盘，以及两个直径为50 mm的铝制质量盘构建转轴。为测试该转轴模态特性，对其进行试验模态分析，通过力锤在质量盘上施加冲击信号，通过加速度传感器同步采集获取振动响应，进而根据输入输出信号可得转轴传递函数幅频特性如图2所示。

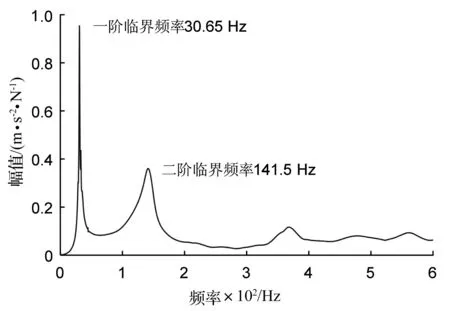
图2 转轴传递函数幅频特性Fig.2 Amplitude-frequency characteristics of the transfer function

将图1所示平台旋转部分归类为弹性轴段、质量圆盘以及支承轴承单元，分别建立各单元微分方程，并在N-1个轴段上按节点顺序对各单元方程进行综合，可得到如式(3)所示的系统动力学微分方程，对该式的齐次式进行求解，可得转子第一、二阶临界共振频率分别为29.97 Hz、143.2 Hz，与图2所示结果对比可知，所构建系统模型精度是可信的。

由于振动测点数量小于不平衡结点数量，需要扩展动平衡转速使式(9)中的系数矩阵满秩，实验中转速分别设置为1 200 r/min和1 600 r/min。根据两个转速下采集的振动数据可构建式(9)中的向量A，根据动力学模型可构建式(9)中的Ψ矩阵，进而对式(9)进行求解可得到四个质量盘所在结点的识别不平量如表1所示。

按表1识别结果在质量盘上反向安装配重螺钉，运行后可得不平衡振动如图3所示。

由图3可知，经动平衡配重后，转子一阶临界处振动被有效抑制，振幅从379.5 μm降至63.19 μm，临界转速前后残余振动也比动平衡前降幅非常明显，表现出良好的动平衡效果，证明了不平衡量识别的准确性。此外，测试转速越高，转子振动越接近临界，采集到的转子振动特性也将越明显；而转速间隔增量越大，式(9)中的矩阵各行元素就越不容易出现病态，这在一定程度上都能提高不平衡识别精度。

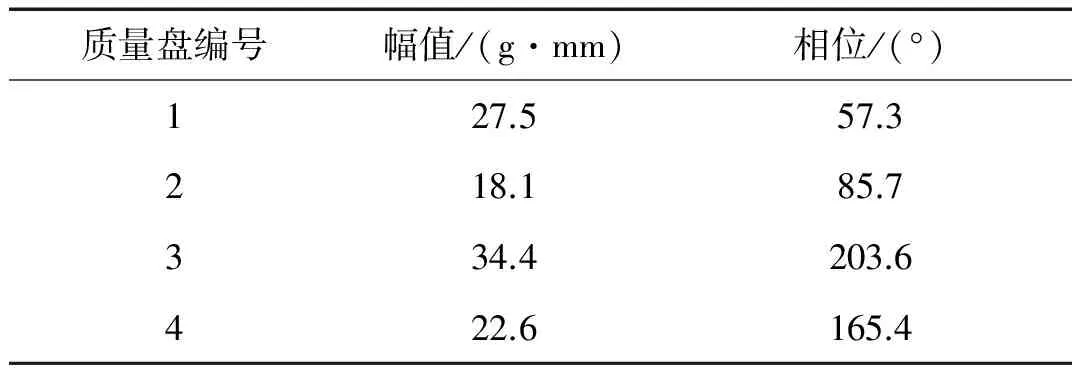
表1 识别不平衡量

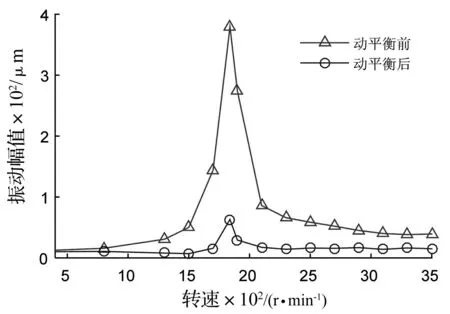
图3 动平衡前后不平衡振动Fig.3 Vibration response before and after dynamic balancing

图3中动平衡后残余振动仍然存在。究其原因，主要在于动平衡精度受到最小平衡配重螺钉质量导致的配重精度偏差、转轴自身存在的弯曲等非失衡故障、加工装配精度以及模型构建偏差等因素影响。

5 结 论

为有效抑制转子分布式不平衡量所致的故障振动，本文提出了一种高速转子分布式不平衡量识别方法，并基于转子平台实例验证了该识别方法的有效性，主要结论如下：

(1)通过对比分析动力学传递函数与影响系数，确定了两者幅值相等，相位相反的关联关系。

(2)提出了一种通过有限元动力学模型结点表征分布式不平衡量的描述方式。

(3)通过增加测试转速数量，可使动力学传递函数矩阵满秩，实现分布式不平衡量解析。

(4)该分布式不平衡量识别方法无需试重，且仅需在低于临界转速时采集振动数据。

在工程应用时，可以根据需要选择合适数量的不平衡量表征结点以及测振结点。对于明确不存在不平衡量的截面，可以在求解过程中略去，以减小求解方程的维数；测振点布置空间较宽裕时，可以适当增加测振点，以减少振动测试的次数。此外，转子工作转速越高，则多次测振对应的转速之间可设置的间隔空间越大，所构建的不平衡量求解方程矩阵越不易呈现病态。因此，该方法更适用于高速转子的动平衡。

[ 1 ] ZHOU S, SHI J. Active balancing and vibration control of rotating machinery: a survey[J]. The Shock and Vibration Digest, 2001,33(4):361-371.

[ 2 ] 章云, 梅雪松, 邹冬林, 等. 应用模态分析及傅里叶变换的柔性转子无试重动平衡方法[J]. 振动与冲击, 2012,31(11):7-10. ZHANG Yun, MEI Xuesong, ZOU Donglin, et al. A field balancing method of flexible rotors based on modal analysis and fourier transform[J]. Journal of Vibration and Shock, 2012, 31(11):7-10.

[ 3 ] EL-SHAFEI A, EL-KABBANY A S, YOUNAN A A. Rotor balancing without trial weights[J]. Journal of Engineering for Gas Turbines and Power, 2004,126(3):604-609.

[ 4 ] RAMLAU R, NIEBSCH J. Imbalance estimation without test masses for wind turbines[J]. Journal of Solar Energy Engineering, 2009,131(1):284-289.

[ 5 ] 王维民, 高金吉, 江志农, 等. 旋转机械无试重现场动平衡原理与应用[J]. 振动与冲击, 2010,29(2):212-215. WANG Weimin, GAO Jinji, JIANG Zhinong, et al. Principle and application of no trial weight field balancing for a rotating machinery [J]. Journal of Vibration and Shock, 2010,29(2):212-215.

[ 6 ] 章云, 梅雪松, 邹冬林, 等. 应用动力学模型的高速主轴无试重动平衡方法[J]. 西安交通大学学报, 2011, 45(7): 34-37. ZHANG Yun, MEI Xuesong, ZOU Donglin, et al. Model-based balancing method for high-speed machine tool spindle without trial weights[J]. Journal of Xi’an Jiaotong University, 2011,45(7): 34-37.

[ 7 ] ZHOU S Y, DYER S W, SHIN K K, et al. Extended influence coefficient method for rotor active balancing during acceleration[J]. Journal of Dynamic Systems, Measurement and Control, 2004,126(1):219-223.

[ 8 ] 钟一谔, 何衍宗, 王正, 等. 转子动力学[M]. 北京: 清华大学出版社, 1987.

[ 9 ] ZHANG Y, MEI X, SHAO M, et al. An improved holospectrum-based balancing method for rotor systems with anisotropic stiffness[J]. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, 2013,227(2):246-260.

[10] SHIN Y, LEE A. Identification of the unbalance distribution in flexible rotors[J]. International Journal of Mechanical Sciences, 1997,39(7):841-857.

[11] YANG T, LIN C. Estimation of distributed unbalance of rotors[J]. Journal of Engineering for Gas Turbines and Power, 2002,124(4):976-983.

An identification method of distributed imbalance without trial weights for high speed rotors

ZHANGYun1，HUZhenbang2，MEIXuesong2

(1. School of Mechano-electronic Engineering, Xidian University, Xi’an 710071, China; 2. State Key Laboratory for Manufacturing Systems Engineering,Xi’an Jiaotong University, Xi’an 710049, China)

To avoid the vibration induced by distributed imbalance, an identification method without trial weights of distributed imbalance for high speed rotors, which only need to collect vibration data below the first critical speed, is presented. First, the relationship between the dynamics transfer function and the influence coefficients was identified based on the dynamics analysis and the extended influence coefficients principle. Second, the mass eccentricity curve of distributed unbalance was described by the nodes in finite element model, and then, a formula to solve the distributed unbalance imposing on each finite element model node was derived from the full rank of dynamics transfer matrix, which was obtained by increasing the speed. Finally, the experiment analysis was performed on a flexible rotor test rig, and the results demonstrated that the magnitude of the vibration during the first order critical speed was reduced significantly after adding the correcting weights, which implied that the distributed unbalance could be identified accurately by the proposed method.

high speed rotors; distributed imbalance; imbalance identification; without trial weights

国家自然科学基金项目(51305324);中央高校基本科研业务费专项资金(JB140408)

2015-11-11 修改稿收到日期：2016-01-27

章云 男，博士，讲师，1983年8月生

TH113.25

A

10.13465/j.cnki.jvs.2017.04.005