SODF-SPH方法及其在热传导问题中的应用

热合买提江·依明 阿合买提江·伊明江 买买提明·艾尼

1.新疆大学数学与系统科学学院，乌鲁木齐，8300462.新疆大学机械工程学院，乌鲁木齐，830047

SODF-SPH方法及其在热传导问题中的应用

热合买提江·依明1阿合买提江·伊明江1买买提明·艾尼2

1.新疆大学数学与系统科学学院，乌鲁木齐，8300462.新疆大学机械工程学院，乌鲁木齐，830047

在光滑粒子流体动力学(SPH)原理的基础上，通过泰勒级数展开提出了计算函数二阶偏导数的SODF-SPH方法。选用相等的粒子间距和相同的光滑长度对一维热传导问题进行了计算和模拟，与传统SPH方法进行了对比分析，结果表明新方法的精度高、收敛速度快且稳定性好；对二维和三维各种热传导问题进行了计算和模拟，与解析解进行了对比，结果表明新方法得到的计算结果与解析解吻合良好。新方法的计算过程能避免计算核函数导数，致使对核函数的要求降低，可选用更多的核函数且计算量较小，可在工程和数值计算中广泛应用。

光滑粒子流体动力学方法；SODF-SPH方法；精度；收敛速度; 稳定性

0 引言

光滑粒子流体动力学(smoothed particle hydrodynamics，SPH)方法是一种新的无网格纯 Lagrange 粒子方法，由LUCY等[1]和GINGOLD等[2]提出，最初用于解决天体物理学和宇宙学中模拟三维无界空间天体的演化问题，之后他们又提出了适用于SPH方法的人为黏性和人为热流项[3-4]，并延伸到了计算流体力学的各个领域。LIBERSKY等[5]在SPH方法中引入了材料强度模型，模拟了动态断裂和破片运动等固体的动态响应，此后SPH也被迅速地应用到固体力学的研究当中。目前，SPH方法已广泛应用于工程计算和模拟的各个领域[6-8]。

随着SPH方法应用范围的扩展和对其研究的不断深入，SPH方法的计算精度和稳定性等方面的缺陷被人们发现，于是研究者用各种方法构造了不同类型的SPH方法，弥补了经典SPH方法的一些缺点[9-11]。SPH方法在应用于热传导问题[12-14]的研究时，二阶偏微分方程被分解为两个一阶偏微分方程，而本文在研究SPH方法的基础上，基于泰勒级数展开构造了直接计算函数二阶偏导数的新SODF-SPH方法，并通过计算和模拟各种热传导问题，来验证SODF-SPH方法解决各种热传导问题的可行性。

1 经典SPH方法

经典SPH方法基本原理比较简单，将任意函数f(x)及其梯度在某一点x处的SPH核近似式，用核函数W(x-x′,h)与f(x)乘积的积分来表示。函数f(x)的SPH核近似表达式为

(1)

式中，〈〉表示函数的核积分近似表达式。

(2)

核函数W(x-x′,h)依赖于两点之间的距离|x-x′|以及核函数影响区域Ω的光滑长度h，因此核函数W(x-x′,h)需满足若干个基本条件[15]。

在SPH方法中把整个求解域离散成一系列任意分布的有质量和容量的有限多个粒子,如图1所示(二维情况)。如果核近似式中粒子j处微元体dx′的体积为ΔVj，质量为mj，密度为ρj，位置坐标为xj，记函数f(x)在粒子j处的值为fj=f(xj)，假设粒子i为中心的核函数影响范围内的粒子总数为M，则函数f(x)在粒子i处的函数及其梯度的粒子和近似式可写为

(3)

(4)

图1 SPH核近似计算示意图Fig.1 SPH kernel approximation

2 SODF-SPH方法的推导

函数f(x) 在x=xi处的泰勒级数展开为

(5)

式中,o(·)表示高阶无穷小。

(6)

由核函数对称性质，式(6)等号右边第二项积分为零。此时整理式(6)得

(7)

由SPH方法的粒子和近似表达式原理与式(7)可得在点x=xi计算函数二阶偏导数近似值的线性方程：

(8)

xji=xj-xi

fji=fj-fi

由以上推导可知，本方法的计算过程可直接代入核函数而无需求其导数，降低了对核函数的要求，使得可选的核函数范围更广；二阶偏导数的计算不必分解成两个一阶偏导数，使得计算速度加快。

3 瞬态热传导方程

在直角坐标系下，瞬态热传导问题的控制方程为

(9)

式中，T为温度;ρ和c分别为材料密度和材料质量热容；λα为沿α方向的热导率；Q为热源强度。

初始条件：T(x,0)=T0，x∈Ω。边界条件：T(x,t)=T1，x∈∂ΓD(Dirchlet边界条件)；T(x,t)n+T(x,t)b=0，x∈∂ΓN(Neumann边界条件)。其中，n为区域Ω边界外单位向量，T(x,t)b为边界热源，∂ΓD∩∂ΓN=∅，∂ΓD∪∂ΓN=∂Ω，∂Ω为区域边界。

4 瞬态热传导问题的SODF-SPH方法

模拟

4.1 误差判断准则

本文通过热传导问题的模拟，将新方法与经典SPH方法对比，对新方法的精度、收敛性和稳定性进行了分析。对不同类型的方法进行比较时，本文以问题解析解与数值解的误差作为判断准则。误差为

(10)

式中，M为整个计算区域内的粒子总数；T(xi)为xi处的解析解；TC(xi)为xi处的数值解。

4.2 热传导问题的模拟

本文所有实例取ρ=1，c=1，λα=1，核函数光滑长度h=1.1Δd(Δd为初始粒子间距)。

4.2.1 一维热传导问题的模拟

实例1 初始和边界条件为T(x，0)=T0，T(0,t)=T0，T(L,t)=T1，此时该问题的解析解[12]为

模拟时,取L=1，T0=0 ℃，T1=1 ℃。

图2给出了设立21个粒子，时间步长t=10-4s时，不同时刻温度曲线的解析解与数值解的对比，结果表明本文方法较经典SPH方法具有更高的精度和稳定性。图3给出了不同时刻分别设立21、41、81、161个粒子时，本文方法与经典SPH方法误差的变化，通过对比发现SODF-SPH方法比经典SPH方法具有更好的收敛性。

图2 不同时刻温度曲线数值解Fig.2 Numerical solutions at different time step

4.2.2 二维热传导问题的模拟

实例2 恒温边界条件热传导问题的模拟：当T(x,y,0)=T0,T(0,y,t)=T(L,y,t)=T(x,0,t)=T(x,H,t)=T1时，问题的解析解[13]为

模拟中取L=1，H=1，T0=100 ℃，T1=0 ℃，模拟中设立51×51个均匀分布粒子，时间步长dt=10-4s。

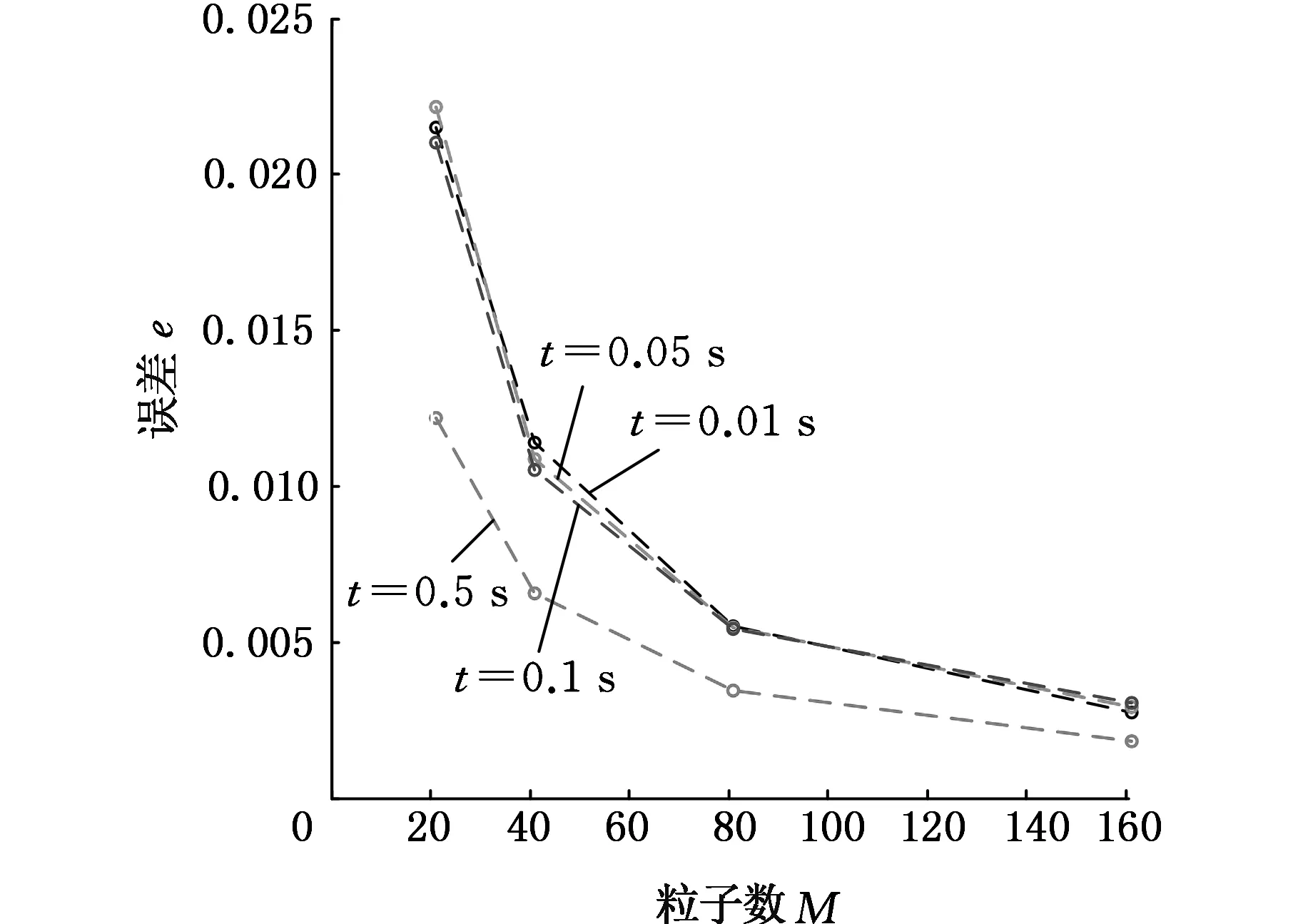
(a)SPH方法

(b)SODF-SPH方法图3 不同时刻不同粒子数的误差对比Fig.3 Errors at different time step and different particle numbers

图4为t=0.1 s时解析解与SODF-SPH数值解的云图，对比发现数值解与解析解几乎完全一样。为了进一步验证数值计算结果的正确性，图5为不同时刻在直线y=x上解析解与SODF-SPH数值结果的对比图，由不同时刻的数值结果对比可以看出，计算结果与解析解吻合良好。

式中，αk、βl分别为超非线性方程αktan(αkL)=b和βltan(βlH)=b的非负解。

模拟中取L=1，H=1，T0=100 ℃，b=0.1，模拟中设立51×51个均匀分布粒子，时间步长dt=10-4s。

(a)解析解

(b)SODF-SPH数值解图4 当t=0.1 s时的温度分布情况(恒温边界问题)Fig.4 Temperature distribution for the constant temperature boundaries at t=0.1 s

图5 不同时刻温度变化情况(y=x)Fig.5 Temperature distribution at different time step (y=x)

图6为t=0.05 s时解析解与SODF-SPH数值解的云图，结果显示绝热边界和对流边界热传导问题的温度等值线分布情况基本一致。此时本文提出方法得到的最高和最低温度分别是Tmax=99.993 205 ℃和Tmin=95.000 652 ℃，而相应的解析解分别为Tmax=99.994 653 ℃和Tmin=95.113 279 ℃，两者也非常接近。以上结果表明用本文提出方法模拟混合边界条件瞬态热传导问题的可靠性。

(a)解析解

(b)SODF-SPH数值解图6 当t=0.05 s时的温度分布情况(对流边界问题)Fig.6 Temperature distribution for the convection boundaries at t=0.05 s

4.2.3 三维热传导问题的模拟

实例4 初始条件为T(x,y,z,0)=sin(πx)+sin(πy)+sin(πz)；边界条件为T(0,y,z,t)=T(1,y,z,t)=(sin(πy)+sin(πz))exp(-π2t)，T(x,0,z,t)=T(x,1,z,t)=(sin(πx)+sin(πz))exp(-π2t)，T(x,y,0,t)=T(x,y,1,t)=(sin(πx)+sin(πy))·exp(-π2t)时，该问题的解析解[16]为

T(x,y,z,t)=(sin(πx)+sin(πy)+
sin(πz))exp(-π2t)

模拟中设立26×26×26个均匀分布粒子，时间步长dt=10-6s。

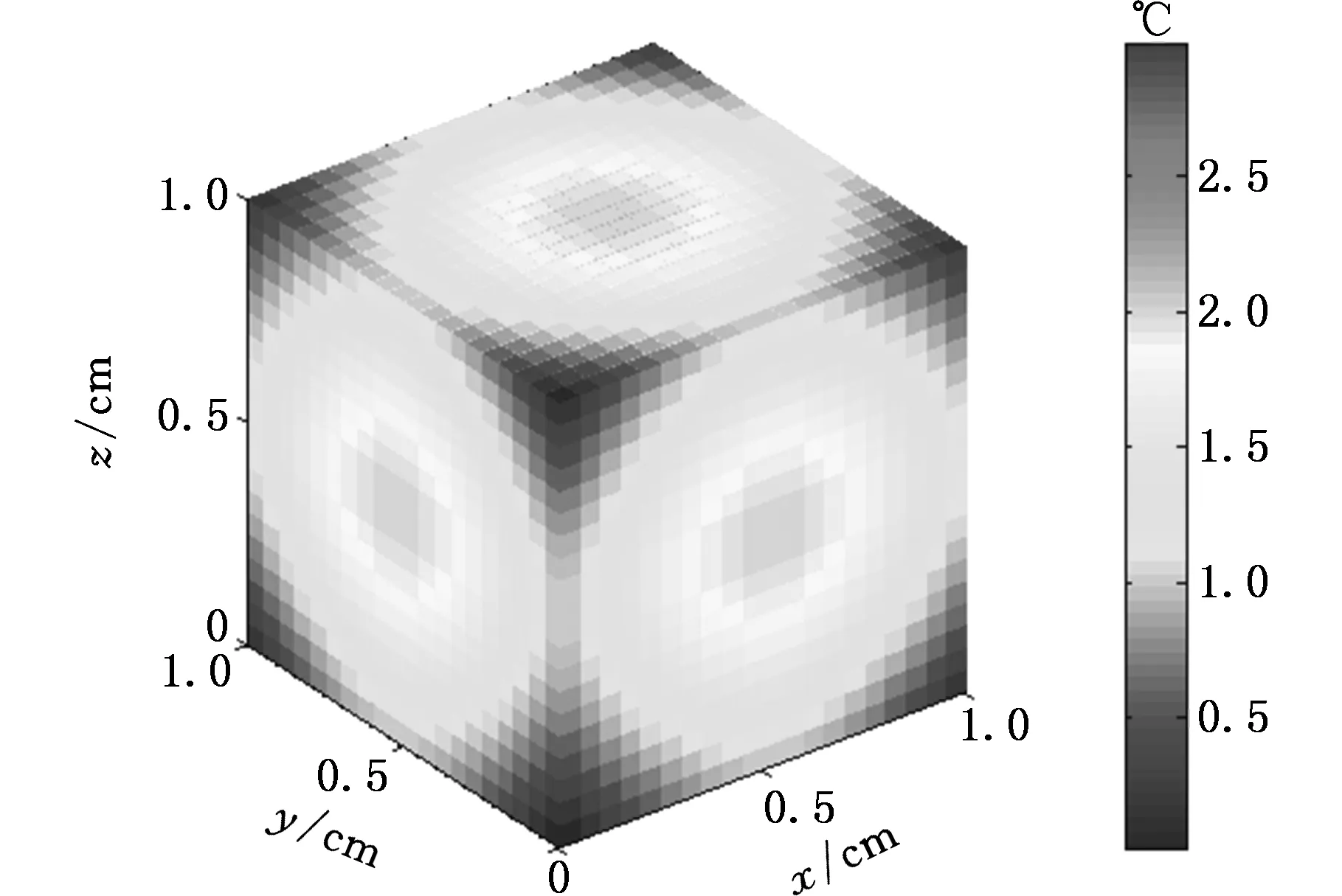
(a)解析解

(b)SODF-SPH数值解图7 当t=0.001 s时的温度分布情况(三维问题)Fig.7 Temperature distribution for the 3D case att=0.001 s

图7给出了当t=0.001 s时的解析解与SODF-SPH数值解，此时本文方法得到的最高温度是Tmax=2.9647 ℃，而相应的解析解为Tmax=2.9516 ℃。因此，对三维热传导问题用SODF-SPH方法所得结果与解析解基本一致。

5 结论

(1)在设立相同的粒子间距、核函数和光滑长度的情况下计算函数二阶偏导数，本文方法比经典SPH方法误差小、稳定性好且收敛速度快。

(2) 用SODF-SPH方法对一维、二维和三维瞬态热传导问题在不同的边界条件下进行计算和模拟，数值解与解析解吻合良好，验证了该方法模拟瞬态热传导问题的可行性。

(3)用SODF-SPH方法进行计算，对核函数导数的要求较低，使得可选的核函数更多，且二阶偏导数的计算速度更快。这一方法具有良好的计算精度和求解能力，有望在复杂的热传导等工程问题中得到应用。

[1]LUCYLB,ANumericalApproachtotheTestingofFissionHypothesis[J].AstrophysicalJournal, 1977, 82(12):1013-1020.

[2]GINGOLDRA,MONAGHANJJ.SmoothedParticleHydrodynamics:TheoryandApplicationtoNon-sphericalStars[J].MonthlyNoticesoftheRoyalAstronomicalSociety, 1977, 181(3):375-389.

[3]GINGOLDRA,MONAGHANJJ.KernelEstimatesasaBasisforGeneralParticleMethodsinHydrodynamics[J].JournalofComputationalPhysics, 1982, 46(3):429-453.

[4]MONAGHANJJ.SimulatingFreeSurfaceFlowswithSPH[J].JournalofComputationalPhysics, 1994, 110(2):399-406.

[5]LIBERSKYLD,PETSCHEKAG.SmoothParticleHydrodynamicswithStrengthofMaterials[J].LectureNotesinPhysics, 2006, 395:248-257.

[6]STOWED,KUPSCHELLAR,PANH,etal.InvestigationofS-SPHforHypervelocityImpactCalculations[J].ProcediaEngineering, 2015, 103:585-592.

[7]NAIRP,TOMARG.AnImprovedFreeSurfaceModelingforIncompressibleSPH[J].Computers&Fluids, 2014, 102:304-314.

[8]CHENZ,ZONGZ,LIUMB,etal.AnSPHModelforMultiphaseFlowswithComplexInterfacesandLargeDensityDifferences[J].JournalofComputationalPhysics, 2015, 283(C):169-188.

[9]CHENJK,BERAUNJE,CARNEYTC.ACorrectiveSmoothedParticleMethodforBoundaryValueProblemsinHeatConduction[J].InternationalJournalforNumericalMethodsinEngineering, 1999, 46(2):231-252.

[10]ZHANGGM,BATRARC.ModifiedSmoothedParticleHydrodynamicsMethodandItsApplicationtoTransientProblems[J].ComputationalMechanics, 2004, 34(2):137-146.

[11]ZHANGGM,BATRARC.SymmetricSmoothedParticleHydrodynamics(SSPH)MethodandItsApplicationtoElasticProblems[J].ComputationalMechanics, 2009, 43(3):321-340.

[12]JEONGJH,JHONMS,HALOWJS,etal.SmoothedParticleHydrodynamics:ApplicationstoHeatConduction[J].ComputerPhysicsCommunications, 2003, 153(1):71-84.

[13]ZHANGX,ZHANGP,ZHANGL.AnImprovedMeshlessMethodwithAlmostInterpolationPropertyforIsotropicHeatConductionProblems[J].EngineeringAnalysiswithBoundaryElements, 2013, 37(5):850-859.

[14] 蒋涛, 欧阳洁, 栗雪娟,等. 瞬态热传导问题的一阶对称SPH方法模拟[J]. 物理学报, 2011, 60(9):49-58.JIANGTao,OUYANGJie,LIXuejuan,etal,TheFirstOrderSymmetricSPHMethodforTransientHeatConductionProblems[J].ActaPhysicaSinica, 2011, 60(9):49-58.

[15]LIUGR,LIUMB.SmoothedParticleHydrodynamics:aMeshlessParticleMethod[M].Singapore:WorldScientificPublishing, 2003:150-156.

[16]CHANGCW,LIUCS.ANewAlgorithmforDirectandBackwardProblemsofHeatConductionEquation[J].InternationalJournalofHeat&MassTransfer, 2010, 53(23/24):5552-5569.

(编辑 王旻玥)

SODF-SPH Method and Its Applications in Heat Conduction Problems

Rahmatjan IMIN1Ahmatjan IMINJAN1Mamtimin GHENI2

1.College of Mathematics and System Science, Xinjiang University,Urumqi,830046 2.School of Mechanical Engineering, Xinjiang University,Urumqi,830047

Based on the principles of SPH method, a SODF-SPH method to compute second order derivatives was constructed through Taylor series expansion. Equal particle distance and same smoothed length were chosen to compute and simulate 1D heat conduction problems. After compared with conventional SPH method, results show that the accuracy, convergence rate and stability of the new method are better. To compute and simulate 2D and 3D heat conduction problems and compared with analytical solutions, the numerical results are in accord with analytical solutions. The derivatives may avoid calculating differential coefficients of kernel function. Therefore, the demands of kernel function are reduced, more kernel functions may be used and the calculation amounts are decreased. The new method may be widely used in engineering fields and numerical calculations.

smoothed particle hydrodynamics (SPH) method; second order derivative free SPH (SODF-SPH) method; accuracy; convergence rate; stability

2016-06-16

国家自然科学基金资助项目( 51565054, 51075346)；新疆大学博士毕业生科研启动基金资助项目(BS150210)

TH212；TH213.3

10.3969/j.issn.1004-132X.2017.04.007

热合买提江·依明，男，1974年生。新疆大学数学与系统科学学院副教授、博士。主要研究方向为机械优化设计、工程数值计算及其模拟。发表论文20余篇。E-mail:rehmatjanim@xju.edu.cn。阿合买提江·伊明江，男，1969年生。新疆大学数学与系统科学学院副教授。买买提明·艾尼，男，1958年生。新疆大学机械工程学院教授、博士研究生导师。