基于复杂网络的装备保障体系协同保障模型研究

邢彪， 曹军海， 宋太亮， 陈守华， 董原生

(1.装甲兵工程学院 技术保障工程系， 北京 100072; 2.中国国防科技信息中心， 北京 100142)

基于复杂网络的装备保障体系协同保障模型研究

邢彪1， 曹军海1， 宋太亮2， 陈守华1， 董原生1

(1.装甲兵工程学院 技术保障工程系， 北京 100072; 2.中国国防科技信息中心， 北京 100142)

针对复杂网络相继故障(也称雪崩)一旦发生对网络的稳定性具有极强破坏力这一问题，在分析装备保障网络及保障特性的基础上，基于复杂网络理论建立了符合装备保障特性的相继故障模型；结合我军相关协同保障规则，建立了旨在降低相继故障影响、增强保障网络稳定性的协同保障模型；对建立的军级装备保障体系协同保障模型，给出了其在不完全信息条件下遭受攻击的仿真实验分析。仿真实验结果表明，协同保障能够对重要节点提供重点支援和保护，经协同保障后修复的节点与网络中度值较高的节点具有同等的重要性，对二者进行重点保护能够有效地避免大规模相继故障的发生。

兵器科学与技术； 复杂网络； 装备保障体系； 相继故障； 协同保障

0 引言

装备保障体系是服务于武器装备体系和联合作战体系的开放的复杂大系统，可以看作是由各级作战与保障指挥机关、基层修理分队、各类装备和保障人员、器材仓库等为节点，节点两两之间的连接隶属关系为边构成的复杂网络。复杂网络理论作为研究体系和复杂系统复杂性的新方法和有效工具，已在我军军事领域广泛应用[1-3]。近年来国家及中央军委日益重视装备成体系保障能力的建设，提出装备保障要以贴近实战为目标、走军民融合创新发展的道路[4]，因此研究更贴近实战情况下的不完全信息攻击策略和军民融合的协同保障策略对装备保障网络稳定性的影响，具有非常重要的理论和现实意义。

无论是现实中的装备保障网络实际情况，还是单纯的复杂网络理论研究，相继故障对网络稳定性的影响都十分巨大。相继故障是指网络中某一个或某一些节点和边发生故障，会通过网络之间的耦合关系引发连锁反应，最终导致大面积的节点甚至整个网络的崩溃，有时也称“雪崩”。国外较为典型的相继故障模型有Motter等[5-6]提出的容量与初始负载相关的ML模型，和在此基础上Crucitti等[7-8]提出的基于边传输效率动态更新的CLM模型、Li等[9]提出的节点容量与节点度相关的LW模型、Lehmann等[10]提出的随机负载重分配策略、Wang等[11]提出的最近邻负载重分配模型。国内徐野等[12-13]研究了不同网络负载和网络冗余在随机攻击、蓄意攻击、混合攻击等条件下网络相继故障模型；郭迟等[14]提出了一种流量相互补偿算法下的负荷- 容量模型，并确定了冗余资源条件下网络鲁棒性的容量最优分配策略；宋毅等[15]基于时态知识和区间代数方法，构造了一种基于时序特征的网络相继故障模型；沈迪等[16]引入成本惩罚函数构建了军事信息栅格级联失效模型；吴润泽等[17]提出一种考虑级联失效的耦合网络节点重要度评估方法。

但国内以上模型方法的不足之处均是缺少对相继故障后网络应急响应与恢复策略的研究，尤其是在装备保障领域，尚未有针对相继故障(级联失效)现象的有效解决策略。因此基于上述分析，本文在经典的ML模型基础上，先建立适用于装备保障网络的相继故障模型；然后分析保障网络在不完全信息攻击下的相继故障过程，并结合我军目前装备保障活动中有关协同保障的相关准则，建立装备保障体系的协同保障模型；最后通过仿真方法分析对关键节点进行支援和对故障后的节点进行修复的协同保障策略，对减少网络相继故障发生的频率和频次的影响，增强网络的稳定性。

1 装备保障体系复杂网络分析

目前国内关于装备保障体系并没有统一的概念，本文在归纳了大量有关装备保障领域的参考文献的基础上，结合体系的4大基本特征，对装备保障体系作如下定义。

装备保障体系，是指为了满足不同保障任务需求，由具有一定功能和相互联系的各级各类装备保障系统，按照装备保障规律和保障原则综合集成的有机整体。

1.1 装备保障体系网络化

近年来随着信息技术的发展以及作战模式的转变，对应的传统的1对1、分割独立的保障模式也正逐步向网络化、一体化保障模式转变。装备保障体系是以完成规定的保障任务为目标，充分利用分散在整个作战地域不同装备保障力量单元，进行资源协同或调度优化，最终以达到装备保障效益最大化。从复杂网络的视角来看，则是根据实际的装备保障需求，通过集中式或分布式的信息控制分散于不同地域的各级保障节点，最终实现纵横结合、多边协作与资源共享。装备保障体系具有如下复杂网络特征：

1)复杂性。装备保障体系是由若干有限的装备保障单元(节点)组成，并通过装备保障单元之间的互动推动体系涌现出复杂特征并凸显出网络的分布特征。其中，节点类别、业务活动以及规模的差异性组成了装备保障体系整体的复杂性。

2)适应性。装备保障单元既具有自律、自适应和自我调节功能，又具备与外界环境进行信息、能量和物质交换的功能，每个节点的变化都可能受到其他节点变化的影响，并有可能引起其他节点的变化。

3)演化性。装备保障体系是动态的、柔性的、有序的，并通过内部节点之间的相互作用和与外界环境的交互而不断调整网络结构和功能，表现出很大的不确定性。

4)层次性。装备保障体系中存在的一些关键节点或由关键节点组成的局部网络在整个体系中占据着比较重要的空间位置，对体系结构或功能的实现发挥着重要的作用，并且如果这些关键节点出现故障或被攻击，整个体系将有可能崩溃(见图1)。

5)网络性。最后，装备保障体系可看做是由不同功能并且具备半自主性节点构成的网络，在以往的复杂网络研究中都是由同质节点构成，并且单个节点脱离网络后不具备独立的功能。而在装备保障体系中每个保障节点都具有自己的任务和目标，并具有相对独立的保障功能。

1.2 体系复杂网络拓扑结构

以某集团军装备保障体系为研究对象，为了丰富研究的全面性同时考虑保密需要，假设某集团军下属机步师、摩步师、装甲旅、机步旅各一，结合其他军直属单位和各级器材仓库，重点描述装备保障网络中各节点的连接关系，得到军级装备保障体系复杂网络拓扑结构如图2所示。图2中红色节点表示总部、军区等器材仓库(ZB-ZH1、ZB-ZH2、ZB-ZH3)，军区修理大队(ZQ-XLDD)、装备大修工厂(ZQ-XL(ZJ)-XL(CL))等基地级保障机构；蓝色、黑色等保障节点分别对应集团军范围内军(J)、师(S)或旅(L)等各中继级保障机构；黄色保障节点对应团级(T)各基层级保障机构，主要是各修理连。同时，绿色、深绿色等保障节点代表可遂行伴随(BS)保障、完成机动(JD)任务的保障节点，即模型中可进行协同保障的节点，其余均代表该保障网络在一定时期范围内的固定保障节点。

图2(a)实际连接关系包括装备保障网络中各节点彼此之间的指挥隶属关系、指挥信息和保障信息传递、保障任务需求、保障资源调度等复杂连接关系，图2(b)中对图2(a)进行了简化处理，将以上复杂连接关系都赋予到节点的不同级别、性质等属性之中，仅考虑地理空间分布的网络连接关系。建立的军级装备保障体系复杂网络拓扑结构中，最小的保障单元为基层修理分队—修理连，保障资源单元为相应级别的器材仓库。保障资源单元同时存在上下级的隶属关系，并分别与对应的指控单元和基本保障单元连接，受领命令并提供保障资源。仅考虑体系网络中的网络连接关系，建立的军级装备保障体系网络初始的主要性能参数为：节点121，边167.

图2 军级装备保障体系拓扑结构图Fig.2 Topological structure for corps equipment support system of systems

2 装备保障体系相继故障模型

对于一般网络，在初始阶段每个节点或边都承载一定的负荷，网络处于稳定状态，当对其中某一个节点或边进行某种攻击致其故障，失效节点或边上的负荷会分配到邻居节点或边上。对于邻居节点或边而言，当它接受的新增负荷同时加上原有的初始负荷，超出其所能承受最大负荷时，会导致该节点或边故障，从而导致负荷的再次重新分配。直至网络中所有节点和边的负荷均不超出其承载范围时，相继故障结束，网络到达稳定状态。

由此可见，网络中节点或边所能承受负荷能力的水平，对于相继故障能否发生至关重要。定义在装备保障体系网络中，初始阶段每一保障单元均承担一定的保障任务，当某一保障单元遭受指向性攻击发生故障时，其所保障的作战单元会转而连接相邻的其他保障单元。对于相邻的保障单元而言，当它接受的新增保障任务同时加上原有的初始保障任务，超出其自身所能承受最大保障能力时，会导致保障任务无法完成，从而导致保障任务重新分配，直至网络达到稳定状态。这时，如果后方就近派出保障支援力量，承担受损保障单元的保障任务，能够极大地避免相继故障的发生。

定义1 同性质的节点负荷能力(保障能力)相同，不同性质的节点不能互相比较。在装备保障体系3大网络中的指控单元、基本保障单元和保障资源单元分别承担不同的保障任务，如某基本保障单元节点故障，其保障任务应分配到相邻同性质的基本保障单元上，而不能分配给指控单元和保障资源单元。

定义2 在同性质条件下，同级别的保障单元具有相同的保障能力，不同级别的保障单元，级别越高的所能承担的保障能力越大。将各保障单元抽象为网络中的节点，保障单元之间的连接关系抽象为边，假设该保障网络中每一节点i的初始保障能力Li与其级别存在以下数学关系：

Li=λkα+β,

(1)

式中：λ为级别倍乘系数，取值范围[1, 3]；k为节点的度，即网络中与该节点相连边的数量，显然度值越高的节点在网络中重要程度越高；α为指数系数，取值范围[0, 1]；β为衰减系数，服从衰减方程β=1/(1+exp(-gk/sum(k)))[14]，g为常数。

定义3 故障节点i的保障任务重新分配到其临近同性质节点j上，存在择优连接概率p1和p2.p1表示不同级别、不同性质的节点在考虑其空间距离下的静态择优连接概率；p2表示考虑节点度变化的动态择优连接概率。其表达式分别为

p=ap1+bp2,

(2)

式中：a+b=1；

(3)

(4)

(3)式中，当节点性质相同时q=1，当节点性质不同时q=0；lij表示两节点间平均路径长度。(4)式中，ki表示节点i的度，∑K为所有节点度之和。lij计算公式为

(5)

式中：N为网络中节点总数；dij表示两节点间最短路径。

由此可以得出，当节点i故障后，其相邻节点j增加的负荷ΔLj为

(6)

当Lj+ΔLj>maxLj时，节点j发生相继故障，同时节点上的负荷将重新分配。maxLj为该节点最大负荷允许值，由节点的性质、级别等属性决定。

3 装备保障体系协同保障模型

3.1 协同保障定义及策略

共识问题，首先在数学界受到关注。早在1959年，EISENBERG E和GALE D研究了特定条件下如何在一组个体中形成共识概率分布问题。随后共识问题受到了不同学界的广泛关注。

定义装备保障体系协同保障模型存在以下3种支援和协同保障策略：

1)严格按照隶属关系实施保障。现实表征为当某基层级保障节点失效后，由其直属上级中继级保障机构实施支援和协同保障，当中继级不能完成时，任务量继续向上流动，直到最顶层。过程中若任务量分配完毕，则该节点功能恢复，否则该节点故障。

(7)

式中：liij表示存在直接隶属关系的两节点i和j之间的路径长度；V表示网络中所有节点的集合。

2)突出时效性(距离优先，打破建制)。现实表征为对某一故障节点，将其所承担的任务按距离分配。具体为遵循最大饱和原则，将该节点承担的任务量依次分配到距离其最近的保障节点上，以突出时效性。过程中若任务量分配完毕，则该节点功能恢复，否则该节点故障。具体表现为

(8)

式中：lpij表示不考虑隶属关系而以距离优先的两节点i和j之间的路径长度。

3)综合策略。既考虑保障节点之间的隶属关系，又考虑保障节点之间的空间距离，虽然就功能恢复的角度而言，其可能不是最优的，但是却是最可能接近现实的。具体的数学表示为

(9)

式中：α+β=1；xj≥xi表示只能由更高一级或同级的保障节点对失效保障节点实施支援或协同。特别地，当出现两个或两个以上保障节点失效，保障资源请求发生冲突时，以保障任务重要度大的节点进行优先支援或协同，若重要度相同则进行随机选择。

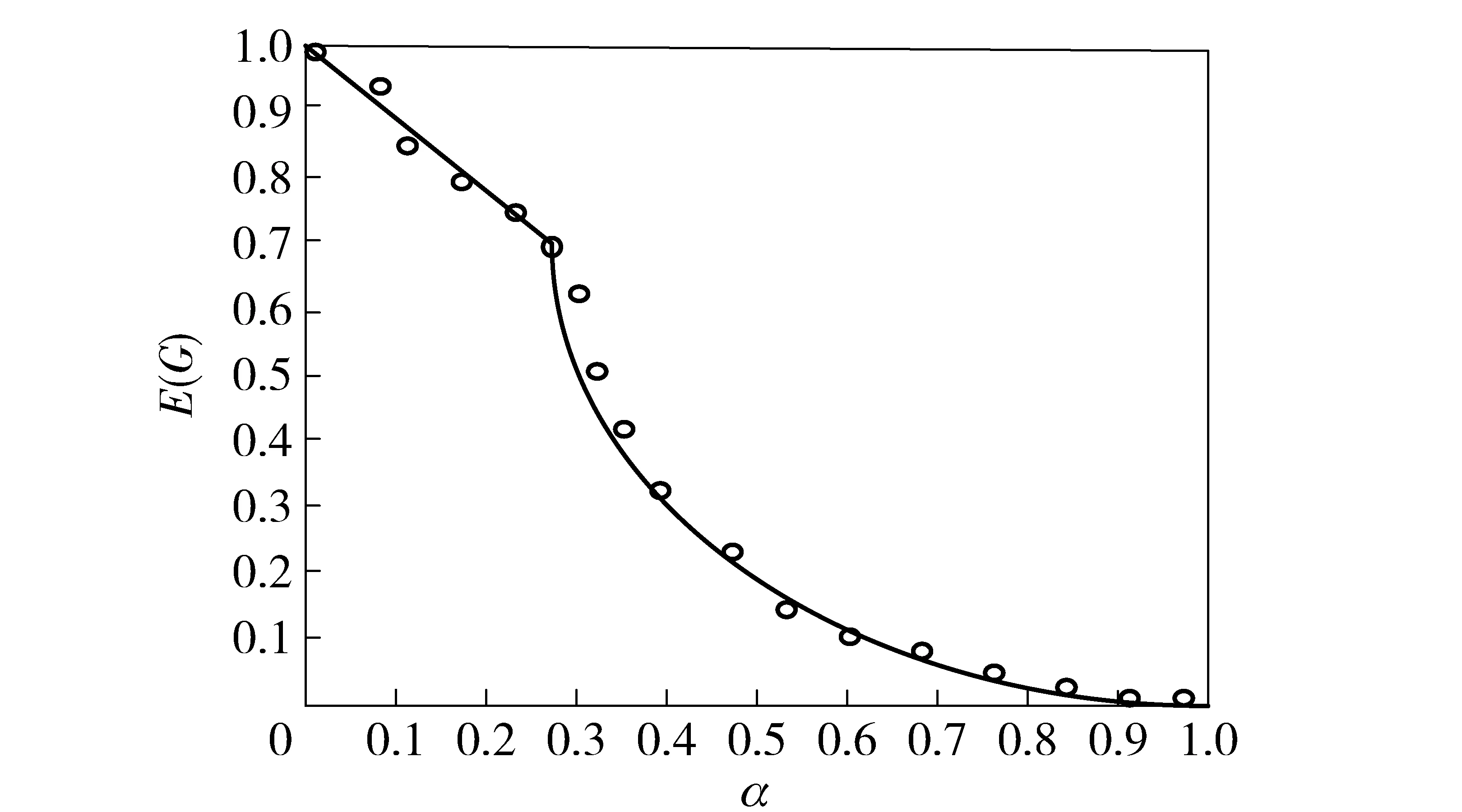
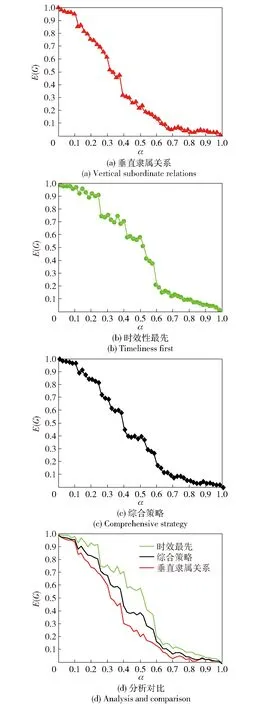
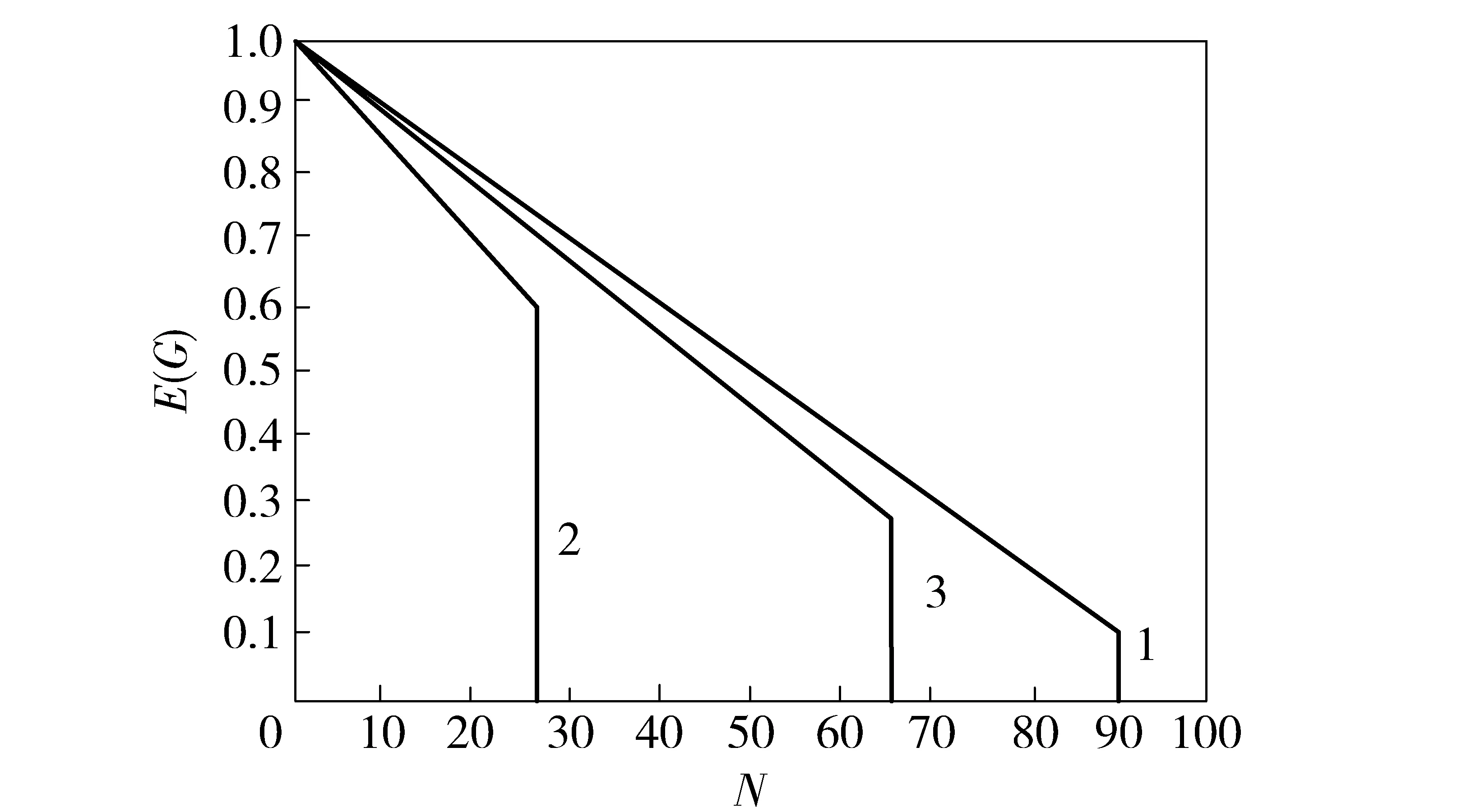
定义4 当协同保障模型中存在Lj+ΔLj=η·maxLj时，进行协同保障，目的是增大已故障或临近故障节点的固有maxLj的值，避免相继故障发生，η取值范围 [0.9, 1)。协同保障的规模或力量用ΔLs表示，对于向外输出协同保障力量的节点，必须首先保证该节点自身无故障，即满足Lj+ΔLj+ΔLs

ΔLs=(1-η)·(Lj+ΔLj).

(10)

当对网络信息一无所知时，进行无差别随机攻击网络中的节点和边，属于零信息攻击；当获得网络的整个结构信息时，按节点度和边的重要程度进行指向性优先选择攻击，属于完全信息攻击。目前国内关于网络攻击模式的研究主要有随机攻击和蓄意攻击两种，但这两种本质上都是极端的攻击模式。张超等[18]将二者结合建立了一种先优先选择攻击网络中已知信息节点(按网络中节点重要度从大到小依此打击)，再随机攻击未知节点的算法模型。吴俊[18]提出了通过信息精度参数和信息广度参数，将网络信息抽象为无放回的等概率抽样问题。显然在实际战争中由于战争迷雾的存在，更贴近实战的情况是不完全信息攻击。在不完全信息条件下对复杂网络的攻击，主要取决于两方面要素：一是敌方获取我方信息区域的范围；二是敌方采用的攻击模式。

定义5 已知信息区域范围Ω是指该区域内所包含的节点数量和这些节点的性质、级别等属性。节点数量由系数μ决定，μ∈[0,1]，显然μN即为区域Ω的大小，节点的性质、级别等属性由精度参数δ决定。首先对所有节点按其节点度值由大到小顺序进行排序，构造序列函数ri，节点度值相同节点按级别由高到低、性质按指控、修理、供应的顺序排列；然后定义δ∈[0,+∞)，得到节点精度抽样概率wi如(11)式所示，显然在此算法约束下，网络中节点度值越大、重要程度越高的节点被抽中的概率越大。

(11)

定义6 确定攻击模式为第1阶段优先选择攻击网络中已知信息区域内的节点(按网络中节点重要度从大到小依此打击)，第2阶段随机攻击剩余区域的所有未知节点，当节点遭受攻击发生故障后，移除该节点以及所有与该节点相连接的边。考虑到协同保障模型，对进行协同保障后能够避免故障甚至一定程度上恢复保障能力的节点进行动态条件选择攻击，攻击概率为

P(x)=λe-λwi.

(12)

3.3 网络演变过程划分

按照以上建立的装备保障体系协同保障模型，将不完全信息条件下体系网络遭受攻击后的演变过程划分为5个阶段：

1)稳定保障阶段。初始阶段装备保障体系内所有保障单元均在其所承担的保障任务范围内进行保障活动，网络处于稳定状态。

2)相继故障阶段。当网络中某一节点遭受不完全信息攻击发生故障后，其所承担的保障任务按择优连接概率分配到相邻的同性质节点上，如发生相继故障则进行再次分配。

3)协同保障阶段。上级支援保障力量和同级保障力量在自身无故障的前提下，可对已故障节点或临近故障节点进行支援，通过进行协同保障，一定程度上恢复该节点的保障能力。

4)重点攻击阶段。经过协同保障后，对免于故障甚至一定程度上恢复保障能力的节点进行再次动态条件选择攻击，攻击后节点如未发生故障则进入阶段5，如发生故障则重复阶段2和阶段3.

5)故障终结阶段。此时网络如承受住此轮不完全信息攻击，则达到新的稳定保障阶段，继续执行保障任务；如大部分网络节点或边故障，节点故障数量超出总节点数量90%时，网络瘫痪，失去保障能力。

3.4 鲁棒性度量方法

鲁棒性是衡量体系网络可靠性和稳定性的重要指标，装备保障体系网络能否具备较高的鲁棒性，直接决定了保障网络遭受打击后的抵抗能力。如果装备保障体系网络的鲁棒性较差，将直接导致武器装备无法发挥保障能力，进而影响作战性能的发挥，甚至造成网络瘫痪，决定战争结局。目前国内张超等[19]、王正武等[20]、徐凤等[21]、刘刚等[22]、陆余良等[23]分别分析了航空通信网络、城市道路网络、高铁- 民航复合网络、铁路换乘系统网络、局域路由系统等考虑级联失效的鲁棒性分析方法。但以上方法主要从理论分析和攻击策略等方面进行研究，就度量指标而言，一般都是通过探测网络连通性作为鲁棒性的判断依据，而较少考虑网络受到破坏后的恢复能力。因此本文结合以上方法的优点，研究经过协同保障后网络的恢复鲁棒性，提出了以下度量指标：

定义7 网络的恢复鲁棒性是指当网络中某些节点故障后，通过协同保障能对故障的节点进行恢复使其能够继续执行保障任务的能力。节点的恢复鲁棒性D和边的恢复鲁棒性E分别为

(13)

(14)

式中：Nr和Mr分别为网络中故障节点和边数量；Nd和Md分别为协同保障后修复的节点和边数量；N和M为网络中节点和边总数量。

同时，可用网络效率度量网络的鲁棒性，定义网络效率E(G)计算公式为

(15)

4 仿真案例及分析

图3 网络相继故障规模演化图Fig.3 Evolution process of cascading failure

本文分两种方案研究网络相继故障规模的大小：方案1为考虑不同性质的节点在空间距离下的静态择优连接概率和节点度变化的动态择优连接概率条件下，保障任务的重新分配造成的网络相继故障规模，随α取值变化网络效率E(G)演化如图3所示；方案2为考虑协同保障模型对已故障节点和临近故障节点的修复条件下，造成的网络相继故障规模，如图4所示。

图4 网络相继故障与协同保障演化图 Fig.4 Evolution process of cascading failure and cooperating support

由此可见，网络效率E(G)会随着节点遭受攻击发生故障而下降，初始攻击阶段当攻击值较小时，对整个装备保障体系的影响很小。由图3可知，当α取值达到0.3时就足以使得整个装备保障体系的E(G)下降到50%以下。此时可理解为敌方攻击我方中的一些重要核心保障节点，核心节点的失效在一定程度会影响整个保障体系，引发网络相继故障，使得E(G)下降速率明显加快。此时若经过协同保障后，如图4所示，能够对已故障节点和临近故障节点进行修复，降低E(G)的下降速率，一定程度上能够抑制相继故障的大面积迅速爆发和蔓延。装备保障体系网络效率E(G)下降的态势，在0.41、0.5、0.58、0.67、0.75等处均存在较为明显的上升趋势，正是通过进行协同保障后，对部分已故障节点和临近故障节点进行了修复的效果。说明所设计的协同保障模型是合理、有效的。

接下来进一步按照(7)式、(8)式、(9)式制定的3种支援和协同保障策略，模拟不完全信息条件攻击下对装备保障体系网络效能的影响，如图5所示。

图5 不同协同保障策略下装备保障体系E(G)分析Fig.5 Analysis of E(G) under different cooperating support strategies

由图5可知，考虑时效性优先的协同保障策略明显要高于其他两种保障策略。这是由于如果不考虑组织体制和隶属关系的影响，各个保障节点之间的保障任务流动将更加迅速，整体保障效率将更高。通过图5也可以看出，在这情况下，只要关键核心节点不失效，其整体保障功能基本稳定于某一水平之上。相比较而言，严格按照垂直隶属关系的协同保障策略，由于自身组织体制的刚性和地理空间的分布特性等原因，即使不攻击其中核心节点也可能会导致整体保障功能下降。具体到实际情况为，当攻击较低级别保障节点到一定数量时，由于大量的保障任务不断流向更高级别的保障节点，使得大量核心(基地级)保障节点功能超过其自身最大保障能力而导致失效(体系贡献值角度)。综合策略介于二者之间，在一定程度上可反映目前部队协同保障的实际情况。

最后从另外一个角度验证所建立模型的合理性和有效性，即用网络中摧毁的节点数量来衡量网络整体效率，如图6所示。图6中折线1表示正常情况下复杂网络效率E(G)随故障节点数量的变化，当摧毁网络中90%左右的节点时网络效率降至0.1并处于崩溃状态；折线2是模拟考虑网络中相继故障的发生，当摧毁网络中28%左右的度值较高的重要节点时，虽然E(G)数学计算值为0.6左右，但由于相继故障的发生，已经导致网络处于临近崩溃状态；折线3考虑网络协同保障模型的影响，通过对已故障节点和临近故障节点的修复，当摧毁网络中66%左右的节点时，会导致网络处于临近崩溃状态。

图6 不完全信息条件动态攻击演化图Fig.6 Evolution process under the incomplete information dynamic attack

通过对军级装备保障体系模型进行仿真得出结果如下：

1)通过协同保障模型对重要节点提供重点支援和保护，能够有效地避免大规模相继故障的发生。现实中不同编制体制的保障节点很少或根本不可能发生协同或支援保障关系，但如果在战时条件下，通过一定的组织程序(如逐级或越级上报)，对有互补需求的两个保障单位之间进行协同、支援保障等，能够大大提高保障网络的稳定性。

2)不完全信息条件攻击策略验证了协同保障后修复的节点与网络中度值较高的节点具有同等的重要性，对该修复的节点进行重点攻击同样能够加剧相继故障的发生。

3)在相继故障模型下，网络效率E(G)与节点数量N不再呈简单的正相关，当网络结构确定时，通过协同保障模型来改善保障任务的分配策略，能够更多、更有效率地利用节点的剩余容量，发挥网络潜能，降低网络相继故障规模。

5 结论

复杂网络理论目前已经成为研究复杂系统和体系问题的有效方法，本文主要围绕“怎样避免装备保障体系网络发生大规模相继故障”、“如何更加逼真地模拟战争中装备保障体系网络可能遭受的打击”以及“怎样提高装备保障体系网络的鲁棒性”3个问题，对引起网络大规模相继故障的原因进行了分析，建立了军级装备保障体系网络相继故障和协同保障模型。通过改进的不完全信息条件攻击策略，对协同保障后修复的节点进行动态条件选择攻击。仿真实验结果表明，协同保障能够对重要节点提供重点支援和保护，经协同保障后修复的节点与网络中度值较高的节点具有同等的重要性，对二者进行重点保护能够有效地避免大规模相继故障的发生。下一步的研究方向主要是增加对协同保障的代价(经济性方面)、协同保障的冲突(协同时对同一保障资源的需求)和协同保障的效果的考虑，进一步研究、总结、发现装备保障体系的运行规律。

References)

[1] 胡晓峰, 贺筱媛, 饶德虎. 基于复杂网络的体系作战协同能力分析方法研究[J]. 复杂系统与复杂性科学, 2015, 12(2): 9-17. HU Xiao-feng, HE Xiao-yuan, RAO De-hu. A methodol-ogy investigating the capabilities of command and coor-dination for system of systems operation based on com-plex network theory[J]. Complex Systems and Complexity Science, 2015, 12(2): 9-17. (in Chinese)

[2] 张强, 李建华, 沈迪, 等. 基于复杂网络的作战体系网络建模与优化研究[J]. 系统工程与电子技术, 2015, 37(5): 1066-1071. ZHANG Qiang, LI Jian-hua, SHEN Di, et al. Research on network modeling and optimization of operation system of systems based on complex network[J]. Systems Engineering and Electronics, 2015, 37(5): 1066-1071. (in Chinese)

[3] 徐玉国, 邱静, 刘冠军．基于复杂网络的装备维修保障协同效能优化设计[J]. 兵工学报, 2012, 33(2): 244-251. XU Yu-guo, QIU Jing, LIU Guan-jun. Optimization design on cooperation effectiveness of equipment maintenance support network based on complex network[J]. Acta Armamentarii, 2012, 33(2): 244-251. (in Chinese)

[4] 中华人民共和国国务院新闻办公室. 2015年中国国防白皮书[R]. 北京：新华社, 2015. The State Council Information Office of the People’s Republic of China. China’s National Defense in 2015[R]. Beijing: Xinhua News Agency, 2015. (in Chinese)

[5] Motter A E，Lai Y C. Cascade-based attacks on complex networks[J]. Physical Review E, 2002, 66(6): 065102.

[6] Motter A E. Cascade control and defense in complex networks[J]. Physical Review Letters, 2004, 93(9): 098701

[7] Crucitti P, Latora V, Marchiori M. Model for cascading failures in complex networks[J]. Physical Review E, 2004, 69(4): 045104.

[8] Kinney R, Crucitti P, Albert R, et al. Modeling cascading failures in the North American power grid[J]. Physics of Condensed Matter, 2005, 46(1):101-107.

[9] Li P, Wang B H, Sun H, et al. A limited resource model of fault-tolerant capability against cascading failure of complex network[J]. Physics of Condensed Matter, 2007, 62(1):101-104.

[10] Lehmann J, Bernasconi J. Stochastic load-redistribution model for cascading failure propagation.[J]. Physical Review E Statistical Nonlinear & Soft Matter Physics, 2010, 81(1):227-248.

[11] Wang W X, Chen G R. Universal robustness characteristic of weighted networks against cascading failure[J]. Physical Review E, 2008, 77(2): 026101.

[12] 徐野. 复杂互联系统与网络鲁棒性研究[M]. 北京: 电子工业出版社, 2015. XU Ye. Study of robustness in complex interconnected system and networks[M]. Beijing: Publishing House of Electronics Industry, 2015. (in Chinese)

[13] 徐野, 王瑶. 复杂网络相继故障的节点动态分析[J]. 沈阳理工大学学报, 2015, 34(1): 17-22. XU Ye, WANG Yao. Research of dynamic failure nodes in cascading failure complex networks[J]. Journal of Shenyang Ligong University, 2015, 34(1): 17-22. (in Chinese)

[14] 郭迟, 王丽娜, 李玉, 等. 基于负荷- 容量模型的网络相继故障研究[J]. 计算机研究与发展, 2012, 49(12): 2529-2538. GUO Chi, WANG Li-na, LI Yu, et al. Study on network cascading failures based on load-capacity model[J]. Journal of Computer Research and Development, 2012, 49(12): 2529-2538. (in Chinese)

[15] 宋毅, 王成山. 具有时序特征的相继故障演变模型[J]. 中国电机工程学报, 2008, 28(22): 29-34. SONG Yi, WANG Cheng-shan. A kind of continual fault evolution model with temporal characteristic[J]. Proceedings of the CSEE, 2008, 28(22): 29-34. (in Chinese)

[16] 沈迪, 李建华, 张强, 等. 军事信息栅格级联失效模型及鲁棒性策略研究[J]. 系统工程与电子技术, 2015, 37(2): 310-317. SHEN Di, LI Jian-hua, ZHANG Qiang, et al. Research on military information grid cascading failure model and robustness strategy [J]. Systems Engineering and Electronics, 2015, 37(2): 310-317. (in Chinese)

[17] 吴润泽，张保健，唐良瑞. 双网耦合模型中基于级联失效的节点重要度评估[J]. 电网技术, 2015, 39(4): 1053-1058. WU Run-ze, ZHANG Bao-jian, TANG Liang-rui. A cas-cading failure based nodal importance evaluation method applied in dual network coupling model[J]. Power System Technology, 2015, 39(4): 1053-1058. (in Chinese)

[18] 吴俊. 复杂网络拓扑结构抗毁性研究[D]. 长沙: 国防科学技术大学, 2008. WU Jun. Study on invulnerability of complex network topologies[D]. Changsha: National University of Defense Technology, 2008. (in Chinese)

[19] 张超, 张凤鸣, 王瑛, 等. 基于复杂网络视角的航空通信网络鲁棒性分析[J]. 系统工程与电子技术, 2015, 37(1): 180-184. ZHANG Chao, ZHANG Feng-ming, WANG Ying, et al. Method to analyze the robustness of aviation communica-tion network based on complex networks[J]. Systems Engineering and Electronics, 2015, 37(1): 180-184. (in Chinese)

[20] 王正武, 王杰, 黄中祥. 考虑级联失效影响的城市道路网络容量研究[J]. 土木工程学报, 2015, 48(3): 121-127. WANG Zheng-wu, WANG Jie, HUANG Zhong-xiang. Study on capacity of urban road network considering cascading failure[J]. China Civil Engineering Journal, 2015, 48(3): 121-127. (in Chinese)

[21] 徐凤, 朱金福, 苗建军. 基于复杂网络的空铁复合网络的鲁棒性研究[J]. 复杂系统与复杂性科学, 2015, 12(1): 40-45. XU Feng, ZHU Jin-fu, MIAO Jian-jun. The robustness of high-speed railway and civil aviation compound network based on the complex network theory[J]. Complex Systems and Complexity Science, 2015, 12(1): 40-45. (in Chinese)

[22] 刘刚, 李永树. 基于复杂网络理论的铁路换乘系统鲁棒性分析[J]. 计算机应用研究, 2014, 31(10): 2942-2944. LIU Gang, LI Yong-shu. Robustness analysis of railway transer system based on complex network theory[J]. Application Research of Computers, 2014, 31(10): 2942-2944. (in Chinese)

[23] 陆余良, 杨斌. 域间路由系统级联失效分析与建模[J]. 系统工程与电子技术, 2016, 38(1): 172-178. LU Yu-liang, YANG Bin. Analysing and modeling cascading failures for interdomain routing system[J]. Systems Engineering and Electronics, 2016, 38(1): 172-178. (in Chinese)

Research on Cooperating Support Model of Equipment Support System of Systems Based on Complex Network

XING Biao1, CAO Jun-hai1, SONG Tai-liang2, CHEN Shou-hua1, DONG Yuan-sheng1

(1.Technical Support Engineering Faculty, Academy of Armored Forced Engineering, Beijing 100072, China; 2.China Defense Science & Technology Information Center, Beijing 100142, China)

The cascading failure can lead to a strong damage to the stability of network when it happens. A cascading failure model for equipment support system of systems is established based on the analysis of the support network structure and the actual support condition. And then a cooperating support model is established to reduce the influence of cascading failure and improve the stability of support network. A simulation case analysis for the corps equipment support system of systems cooperating support model is simulated and analyzed under the incomplete information attack. The simulated results show that the cooperating support model is feasible and applicable.

ordnance science and technology; complex network; equipment support system of systems; cascading failure; cooperating support

2016-06-28

军队科研计划项目(51319050302)

邢彪(1988—)， 男， 博士研究生。 E-mail: xingbiao1988@163.com； 宋太亮(1962—)， 男， 研究员， 博士生导师。 E-mail: songtl123@126.com

曹军海(1972—)， 男， 副教授， 博士生导师。 E-mail: jhcao@163.com

TJ810.7

A

1000-1093(2017)02-0374-09

10.3969/j.issn.1000-1093.2017.02.023