舰船地震波传播机理及其在水雷引信中的应用研究
孟路稳, 程广利, 陈亚男, 张明敏
(海军工程大学 电子工程学院, 湖北 武汉 430033)
舰船地震波传播机理及其在水雷引信中的应用研究
孟路稳, 程广利, 陈亚男, 张明敏
(海军工程大学 电子工程学院, 湖北 武汉 430033)
为了给舰船地震波在水雷引信中的应用提供理论依据,基于波动理论推导了两层半无限海洋环境中舰船地震波的激发机理和质点的运动规律,获取了舰船地震波的传播特性。理论分析结果表明:舰船地震波的波动成分有Scholte波和简正波,都存在低频截止和频散现象,当频率增加到一定值后,频散现象消失,且质点的运动轨迹为椭圆;Scholte波的质点振幅离开海底迅速衰减,其能量主要集中在一个波长深度内,并且其横向衰减慢。应用高阶交错网格有限差分法数值模拟了舰船地震波的传播过程,给出了场量的波场快照和时域波形,数值模拟结果验证了理论推导结论。开展了湖试试验,给出了湖底地震波信号的时频分布特性,分析了舰船地震波作为水雷引信接收物理场的可行性。
兵器科学与技术; 舰船地震波; 水雷引信; Scholte波; 简正波; 有限差分
0 引言
水雷武器作为一种性价比比较高的水中武器,自问世以来就受到了各国海军的重视,并取得了相当卓越的战绩。在抗登陆、封锁战役、切断海上交通线等作战中发挥着重要的军事作用。目前水雷引信常用的物理场是舰船的声场、磁场和水压场,但随着消声降噪、消磁等措施的不断完善,使上述物理场在水中引起的场变化减弱,极大地增加了传统水雷引信对舰船的探测难度。同时新技术在扫雷装置中的应用,也使水雷在隐蔽性上面临着严峻的挑战。因此急需研究和开发新的物理场引信,其中美、俄两国已经在水雷中采用海底地震波与声场、磁场联合使用的引信,但出于保密,相关的技术材料未见报道,并且国内对此领域的研究很少。
舰船海底地震波是由舰船航行引起的振动、噪声和水体扰动以压力波的形式经流体介质传播到海底,进而引起海底介质的振动,在海底界面和海底以弹性波的形式向周围传播。舰船海底地震波与天然地震引起的海底地震波类似,只是幅度相对较小。同时降噪处理虽然能有效地减小舰船的高频辐射噪声,但对低频辐射噪声仍很难消除,能否有效地接收并利用舰船的低频段信号,是对舰船目标进行探测的关键。并且浅海波导效应引起的低频截止现象使噪声的低频部分不能在水中传播;此外负梯度水文环境下,声波将急剧折射到海底,声波不能形成有效的远距离传播。而海底地震波则不受水文条件的影响,同时波的频率成分极低,而且相比于体波,海底地震波振幅大,衰减慢,传播距离远,弥补了水声引信的不足。因此开展对舰船海底地震波及其在水雷引信中应用的分析和研究,对我国新型水雷引信的设计、地震波扫雷工具的研制具有重要意义。
目前关于海底地震波引信[1]的文献很少,基本上是对海底地震波的基本概念进行叙述,没有更深入地对海底地震波传播理论和波动成分进行研究。而关于舰船海底地震波的传播特性问题,已公开报道的文献分别从不同角度对其理论进行了研究。文献[2]应用简正波理论分析了分层浅海的声场传播问题,从传播损失的角度论述了海底界面地震波的传播效应,但低于截止频率时,不存在有效的简正波。文献[3]利用数值模拟的方法直观地呈现了多孔海底介质情况下海底地震波的波动成分,但其没有给出相应的时域波形。为了更好地掌握浅海海底地震波的传播特性,本文基于波动理论对海底地震波的成分进行了理论推导,得出了海底界面波的频散方程以及质点的振动位移和运动轨迹,对探测传感器的布放提供了理论依据;同时给出了海底地震波的数值模拟结果,呈现了其时域波形和波场快照,验证了理论推导的结论;研究结果为海底地震波在水雷引信中的应用提供了理论指导和数据支撑。
1 海底地震波理论推导
以波动理论为基础,研究如图1所示的二维半无限海洋环境中海洋声场和海底地震波场的空间分布,建立平面直角坐标系,其中x、z分别为水平距离和垂直深度变量。令x轴位于海水层与海底的交界面,则-H
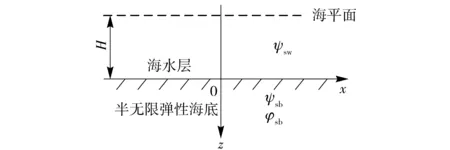
图1 二维浅海简化模型 Fig.1 Simplified model of two-dimensional shallow water
图1中ψsw、ψsb、φsb分别是海水层和海底层的位移势函数,则有以下的亥姆霍兹方程成立[4]:
(1)
式中:ksw,l为海水中纵波的波数;ksb,l、ksb,t分别为海底介质纵波和横波的波数。海底地震波是在海底界面沿轴方向传播且振幅沿垂直方向迅速衰减的一种波,对于简谐波,则有以下位移势函数[5-6]:
(2)
式中:ω为波的角频率;k=ω/v=2πf/v为波数,v为波速;φsw,l、φsb,l和φsb,t是幅度函数。将(2)式代入(1)式,并根据海平面压力为0、无穷远处场量为0、海底界面切应力为0、法向正应力和垂直位移连续的条件,则可得海底地震波的频散方程为
(3)
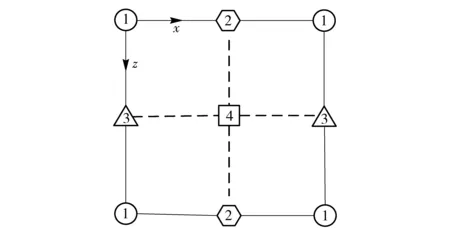
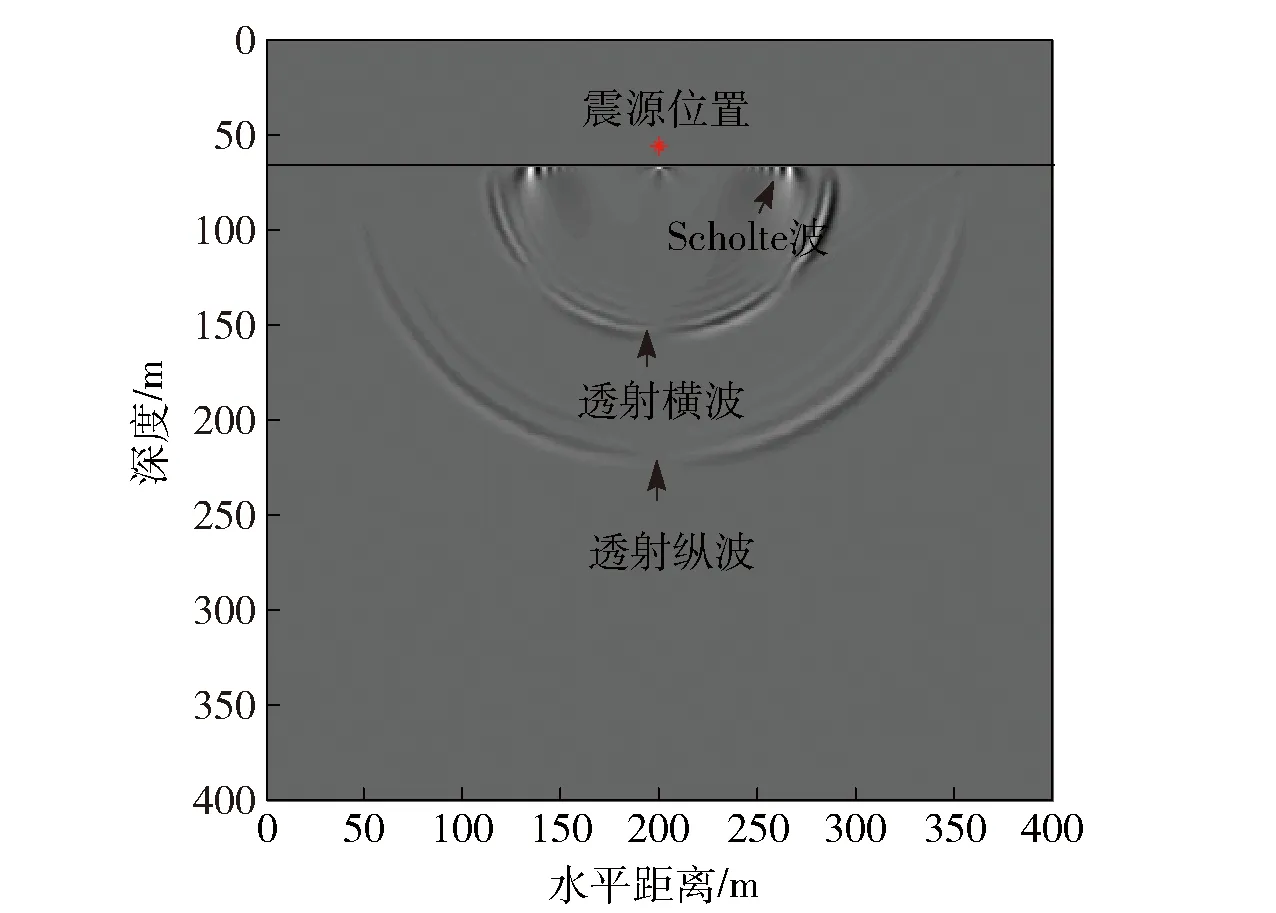
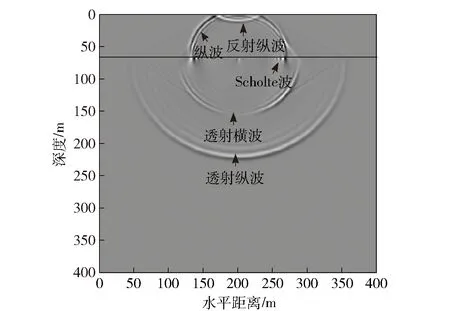
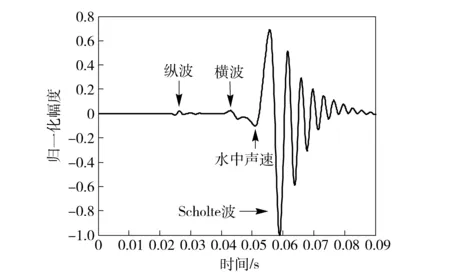
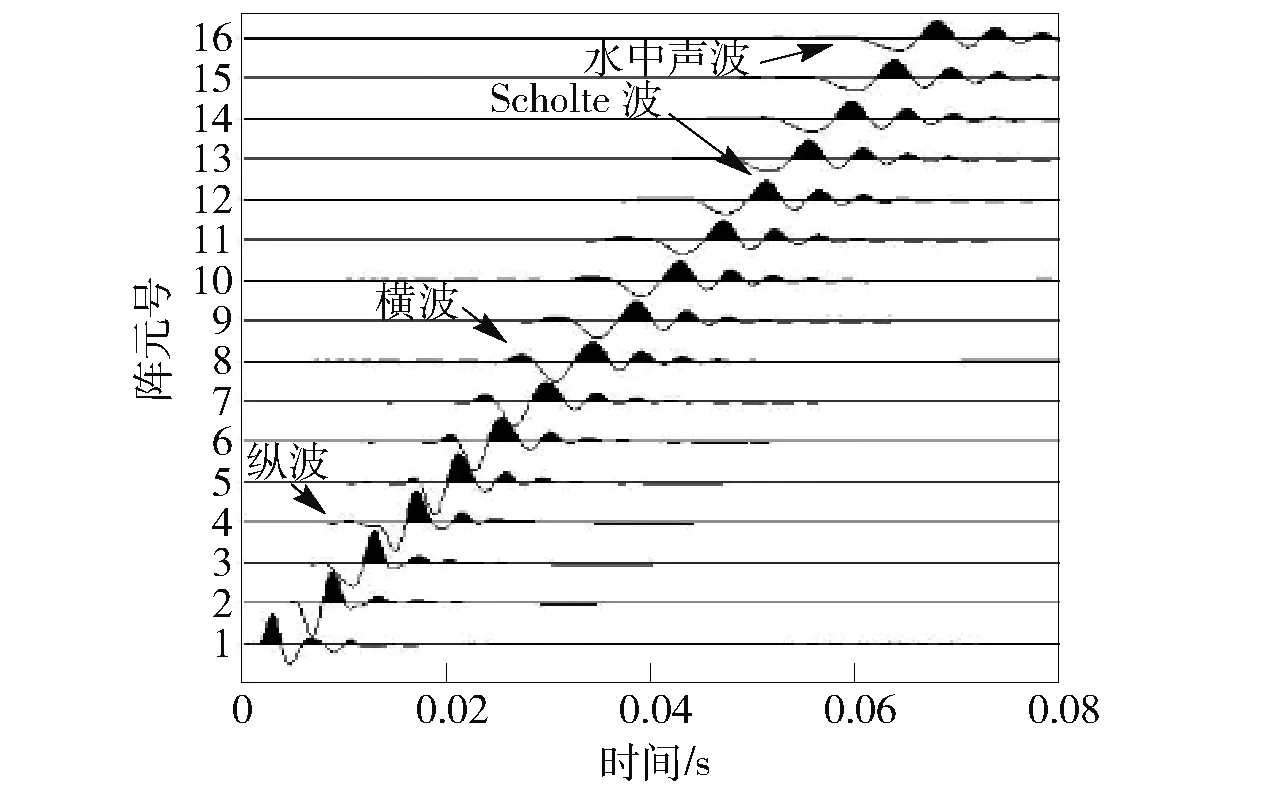
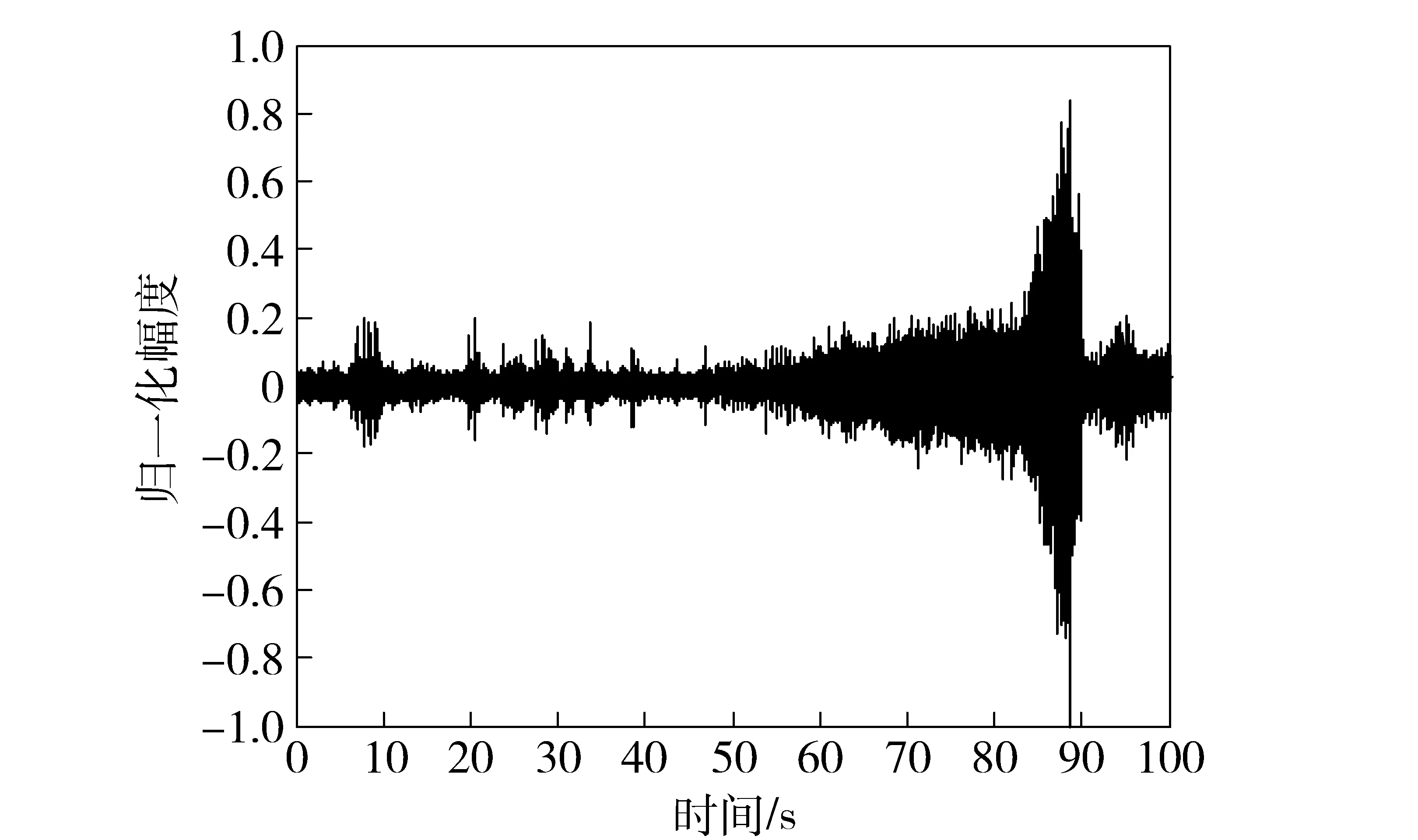
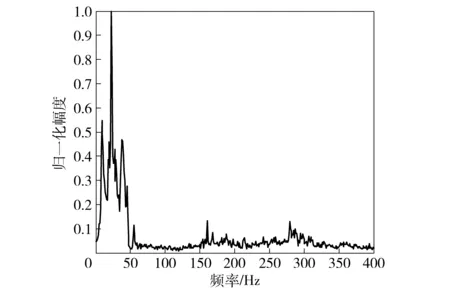
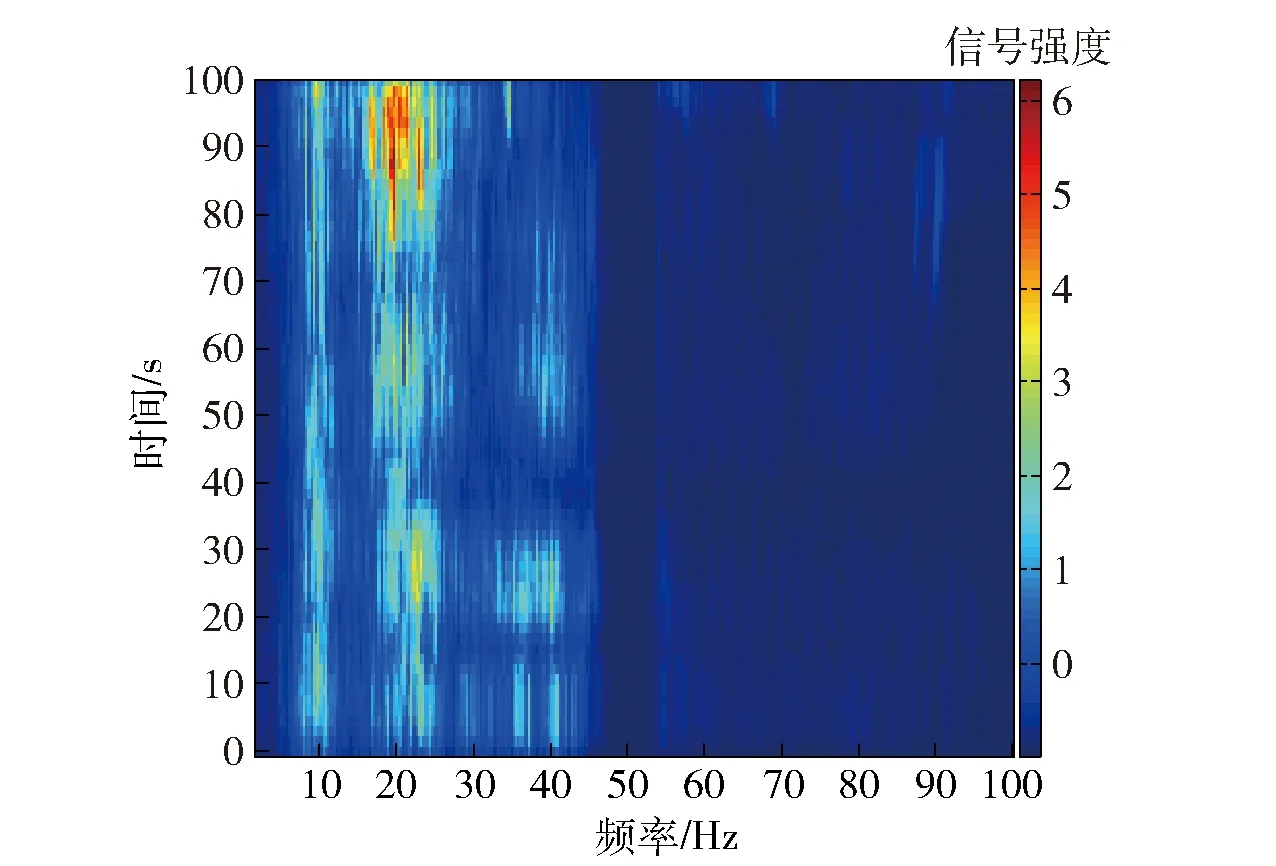
由此可见,海底地震波的波速v与海水深度H和震源频率f有关,并且频散方程(3)式在波速v满足v 高阶交错网格有限差分法以1阶弹性波方程作为基础,通过将空间微分节点移到半节点上来提高精度,在二维交错网格中,正应力σxx、σzz的空间取样位置在整节点上,切应力σxz的空间取样位置在网格的中心,速度vx、vz的空间取样位置在相应轴向棱边的半节点上,相应的弹性波波场分量和弹性参数的空间取样位置见图2和表1. 图2 二维弹性介质交错网格示意图Fig.2 Staggered grid of two-dimensional elastic medium 网格节点1234弹性波场分量和弹性参数σxx,σzz,γ+2μvx,ρ-1vz,ρ-1σxz,μ 根据上述约定,则2N阶空间差分精度、2阶时间差分精度交错网格有限差分格式[8]可表示如下: (4) (5) (6) 式中:Cn为2N阶空间差分精度的差分系数,可通过Taylor公式展开得到[3]。其余波场分量σzz、σxz、vz的差分格式可类比得到。 海水表面为自由表面,则应满足应力为0的自由表面条件。在数值计算时,本文采用横向各向同性介质替换法[8],该方法是用横向各向同性介质近似替代自由表面,即令自由表面处的正应力σzz|z=0=0,而通过设置自由表面上的物性参数使切应力为0,其具体形式为 (7) 式中:ρ、γ表示海水表面上的密度和拉梅常数。 同时海底地震波是在半无限空间区域中传播的,然而高阶交错网格有限差分法是在计算机有限的数据存储空间中对其传播过程在时域上进行数值模拟,则其空间域过大会导致无法在计算机上进行计算,此时只能将计算区域进行截断,变为有限区域。本文采用被广泛推广的完全匹配层[9-11](PML)作为吸收边界。具体的PML差分实现方法见文献[11],这里不再赘述。 在数值模拟时,设置海水深度为60 m,海水密度和声速分别为1 000 km/m3、1 500 m/s;海底介质的密度为2 120 kg/m3,纵波波速和横波波速分别为3 200 m/s、1 700 m/s. 采用时间2阶、空间6阶的交错网格有限差分算法,计算区域为400 m×400 m,PML厚度为10个网格,x和z方向的空间取样间隔均为1 m,时间步长为0.1 ms;震源采用雷克子波,深度设在56 m处,中心频率为20 Hz,其波形如图3所示。 图3 震源波形Fig.3 Source waveform 图4 海底地震波的频散特性曲线Fig.4 Frequency dispersion characteristics of seabed seismic wave 将参数代入频散方程(3)式,则可得海底地震波传播速度的频散特性曲线,如图4所示。由此可见,海底地震波的波动成分有Scholte波和简正波,且都有频散现象,同时当频率增加到一定值后,波速都趋于稳定值。其中Scholte波速度小于海水声速,并且其低频截止频率为3 Hz,当频率无限接近于0 Hz时,Scholte波速度接近于Rayleigh波[6]速度1 577.4 m/s;而简正波速度大于海水声速,小于海底横波速度,并在低频截止频率处趋近于海底横波速度,海水中激发第1~3阶简正波的低频截止频率分别为19 Hz、46 Hz、72 Hz. 图5、图6分别给出了中心频率为20 Hz时,震源激发出Scholte波和简正波的质点位移分布和质点运动轨迹。图5中u、ω分别表示质点的水平位移和垂直位移,用相对位移表示的;z/λ表示深度与波长之比。 图5 Scholte波的质点运动特性Fig.5 Particle motion characteristics of Scholte wave 图6 第1阶简正波的质点运动特性Fig.6 Particle motion characteristics of the first order normal mode 由图5可知:在海水层,Scholte波波动引起的质点水平位移和垂直位移符号相反,且水平位移比垂直位移的振动幅度大;同时二者均随深度的减小呈指数规律衰减,即在海底界面处振幅最大,在海水平面处最小,此时水平位移振幅为0,垂直位移振幅趋近于0;质点运动轨迹在Oxz平面内为一个顺进的椭圆,且椭圆的长轴是水平的。在海底层,质点的垂直位移恒为正值,水平位移由负值逐渐变为正值;质点水平位移和垂直位移的振幅总体上显示出随深度指数衰减的特征,并且Scholte波的能量主要集中在一个波长的深度内;质点轨迹为一个顺进的椭圆,约在z=0.1λ的深度上,质点运动轨迹退化为一条线,之后又变为逆进的椭圆,由于垂直位移的振幅总是大于水平位移的振幅,故椭圆的长轴总是垂直的,并随着深度增加逐渐衰减为0. 在海底界面处,水平位移不连续,垂直位移连续。同样由图6可知:震源在海水中激发出了第1阶简正波,其垂直位移分量在海水层中存在1个振幅为0的波节,质点的垂直位移和水平位移分量随深度呈余弦函数的规律变化;而在海底层,波以界面波的形式出现,质点位移与Scholte波类似。可见对于放置在海底的地震波拾振器来说,以测量垂直速度或垂直加速度为宜;若需埋放在海底,由于在海底位移分量的幅度随着深度的增加而减小,则埋放深度以浅层为最佳。 为了直观地对海底地震波的波动成分进行展示,并且与上述理论分析结果作对比分析,下面给出利用高阶交错网格有限差分法对波场数值模拟的结果。其中图7、图8分别为切应力σxz和正应力σzz在垂直平面内的波场快照。由此可见,海水层中的切应力始终为0,海底层的切应力分量不为0,与理论结果一致,同时震源在海水中激发出声波后,经海平面时发生了反射,产生了反射声波;而经海底界面时,则声波透射到弹性海底进而产生了透射纵波和透射横波;并且在海底界面处形成了Scholte波,其传播速度小于海水声速以及海底介质的纵波、横波速度,与图4中的结论一致,同时其能量主要局限在海底界面附近,随着远离海底界面迅速衰减,与图5中的结论一致。为了得到波场分量的时域波形,在海底界面处沿x轴方向布放接收阵列,一共采用16个阵元接收,阵元间距为5 m,最右侧阵元(令其阵元号为1,向左阵元号依次增加)布放的位置坐标为(200 m,60 m)。因为波场的波动成分传播一定时间后才逐渐分开,为了方便直观地分析各波动成分,图9给出了海底界面上距离震源最远的阵元16记录的时域波形。 图7 切应力σxz的波场快照(t=0.05 s)Fig.7 Snapshot of σxz(t=0.05 s) 图8 正应力σzz的波场快照(t=0.05 s)Fig.8 Snapshot of σzz(t=0.05 s) 图9 阵元16的时域波形Fig.9 Time-domain waveform of array element 16 由图9可知,海底界面上布放阵列接收的波场信号包括海底纵波、海底横波、水中声波以及Scholte波。其中,海底纵波速度最大,首先被接收到,其次是海底横波、水中声波,最后接收到的是Scholte波,且Scholte波的幅度最大。为求解各波动成分的传播速度,下面给出整个阵列记录的时域波形,如图10所示。 图10 整个阵列的时域波形Fig.10 Time-domain waveform of the whole array 由图10可知,各波动成分经一段时间后才逐渐分离开,且随着传播距离的增加而衰减,而Scholte波的衰减相对较慢。通过计算各阵元接收到相同波动成分的时延差,并根据各阵元间距可得到数值计算结果中海底纵波、海底横波和水中声波速度分别为3 214 m/s、1 703 m/s和1 503 m/s,与模拟设置的参数一致,同时Scholte波的速度为1 330 m/s,与图4中理论计算的结果1 328 m/s基本一致,考虑到数值离散的误差,则说明了本文理论推导结论和数值模拟结果的正确性。 为了验证能否接收到稳定的海底地震波信号,在湖中开展了湖底地震波的接收试验。试验中将拾 振器布放在湖底,一艘小船朝着拾振器的方向径向驶来,图11为接收的湖底地震波信号。从中可见信号呈现出由弱变强再变弱的趋势,符合小船和拾振器距离的变化规律,t=88 s时小船行驶到拾振器正上方,信号最强。图12为t=30 s时湖底地震信号的频谱图,由此可见湖底地震波信号的能量主要集中在50 Hz之内,并在23 Hz处最大,50~400 Hz内的能量相对很小。图13为湖底地震波信号的时频图,从中可见湖底地震波的频率成分主要在10 Hz和20 Hz附近,并且在整个时长内很稳定,小船行驶到拾振器正上方,频率成分20 Hz附近的能量明显增强。 图11 湖底地震波信号Fig.11 Signal of lakebed seismic wave 图12 t=30 s时湖底地震信号的频谱Fig.12 Spectrum of lakebed seismic wave(t=30 s) 图13 湖底地震波信号的时频图Fig.13 Time-frequency diagram of lakebed seismic wave 从以上数值计算和湖试数据分析结果可知,舰船地震波具有纵向衰减快、横向衰减慢,频率低等特点,且信号随小船的距离变化具有明显的强弱变化,其可作为沉底水雷引信的接收物理场。与利用声场的水雷相比,此类水雷具有在远距离发现和探测舰船目标的能力以及可利用的频率成分低,且不易受水文条件的影响,因此可作为水声引信的有效补充。 舰船海底地震波作为一种新型物理场,逐渐引起了国内研究人员的关注,对其研究刚处于起步阶段。本文基于波动理论,通过理论分析、数值模拟和湖试试验对可用于水雷引信的海底地震波传播机理和特性进行了分析。首先对海底地震波进行了理论推导,得出了海底地震波的波动成分由Scholte波和简正波组成,给出了质点的位移分布和运动轨迹,为探测仪器的布放提供了理论依据。其次利用高阶交错网格有限差分法对海底地震波的传播过程进行了数值模拟,得到的场量波场快照比较直观地显示了海底地震波的波动成分组成,验证了理论推导的结论;而场量的时域波形为计算波场中各成分的传播速度提供了有效途径。最后开展湖试试验,分析了小船激发的湖底地震波信号的时频分布特性,说明了其可作为沉底水雷引信的接收物理场。 本文利用波动理论分析、数值模拟的方法研究了海底地震波的传播问题,并结合湖试试验数据分析了海底地震波的时频分布特性,为基于舰船地震波物理场的水雷引信设计提供了理论依据和数据支撑,但对拾振器的改善以及接收数据的处理、检测和引信阈值的设定问题,有待进一步的研究。 References) [1] 董立,张健,郭策安,等.地震波引信设计方案的探讨[J].探测与控制学报,2008,30(5):4-6. DONG Li,ZHANG Jian,GUO Ce-an,et al.Research on design scheme for seismic wave fuze[J].Journal of Detection & Control,2008,30(5): 4-6.(in Chinese) [2] 颜冰,周伟,龚沈光.浅海地震波传播的简正波模型[J].武汉理工大学学报,2006,30(5):804-807. YAN Bing,ZHOU Wei,GONG Shen-guang. A normal mode model for ocean seismo-acoustics in shallow water[J]. Wuhan University of Technology,2006,30(5): 804-807.(in Chinese) [3] 卢再华,张志宏,顾建农.多孔介质水平分层海底低频地震波的数值模拟[J].兵工学报,2014,35(12):2065-2071. LU Zai-hua,ZHANG Zhi-hong,GU Jian-nong. A numerical simulation of seismic wave caused by low frequency source in shallow sea with thick porous sediment by staggered-grid finite difference method[J].Acta Armamentarii, 2014,35(12):2065-2071.(in Chinese) [4] Leonardo Z,Laurent D.The method of polarized traces for the 2D Helmholtz equation[J].Journal of Computational Physics,2014,32(9):347-388. [5] Lamkanfi E, Declercq N F, Paepegem W V, et al. Scholte-Stoneley waves on an immersed solid dihedral: generation, propagation and scattering effects[J]. Ultrasonics, 2014, 54(6):1685-1691. [6] Giuseppe R,Vu H N,Salah N.Surface waves at the interface between an inviscid fluid and a dipolar gradient solid[J].Wave Motion,2015,53:51-65. [7] Donald A O,William L S,Michael D C.Scholte-to-Rayleigh conversion and other effects in range-dependent elastic media[J].Journal of Oceanic Engineering,2007,32(3):620-625. [8] 王周,李朝晖,龙桂华,等.求解弹性波有限差分法中自由边界处理方法的对比[J].工程力学,2012,29(4):77-83. WANG Zhou,LI Zhao-hui,LONG Gui-hua,et al.Comparison among implementations of free-surface boundary in elastic wave simulation using the finite-difference method[J].Engineering Mechanics,2012,29(4):77-83. (in Chinese) [9] 徐义,张剑锋.地震波数值模拟的非规则网格PML吸收边界[J].地球学报,2008, 51(5):1520-1525. XU Yi,ZHANG Jian-feng.An irregular-grid perfectly matched layer absorbing boundary for seismic wave modeling[J].Chinese Journal of Geophysics,2008,51(5):1520-1525.(in Chinese) [10] Wang H,Tao G,Shang X F,et al. Stability of finite difference numerical simulations of acoustic logging-while-drilling with different perfectly matched layer schemes[J].Applied Geophysics,2013,10(4):384-396. [11] 秦臻,任培罡,姚姚,等.弹性波正演模拟中PML吸收边界条件的改进[J].地球科学—中国地质大学学报, 2009,34(4):658-664. QIN Zhen,REN Pei-gang,YAO Yao, et al. Improvement of PML absorbing boundary conditions in elastic wave forward modeling[J].Earth Science—Journal of China University of Geosciences,2009,34(4):658-664.(in Chinese) On the Porpogation Mechanism of Ship Seismic Wave and Its Application in Mine Fuze MENG Lu-wen, CHENG Guang-li, CHEN Ya-nan, ZHANG Ming-min (College of Electronic Engineering, Naval University of Engineering, Wuhan 430033, Hubei, China) To provide a theoretical guidance for the application of ship seismic wave in mine fuze, the excitation mechanism and motion law of ship seismic wave in the semi-infinite two-layered ocean environment are theoretically deduced based on wave theory, and then the propagation characteristics of ship seismic wave are also studied. The analysis results show that the ship seismic wave is composed of Scholte wave and normal mode wave, in which low frequency cutoff and frequency dispersion phenomena exist. When frequency increases to a certain value, the frequency dispersion phenomenon disappears, and the motion trajectory of the particle is elliptical. The particle amplitude of Scholte wave decays rapidly away from the seabed and its energy is mainly concentrated in the depth of one wavelength, but its lateral attenuation is small. A staggered grid finite difference method is applied to the numerical simulation of ship seismic wave, and the wave field snapshots and time-domain waveforms are given. The lake trial is carried out, the time-frequency distribution characteristics of lakebed seismic wave signal are presented, and the feasibility of using ship seismic wave as a new physical field of mine fuze is also analyzed. ordnance science and technology; ship seismic wave; mine fuze; Scholte wave; normal mode waves; finite difference 2016-07-27 国家自然科学基金项目(41576105) 孟路稳(1990—) , 男, 博士研究生。 E-mail: mengluwen66@163.com 程广利(1976—), 男, 副教授, 硕士生导师。 E-mail: sonarcgl@126.com 10.3969/j.issn.1000-1093.2017.02.016 TJ43+1.7 A 1000-1093(2017)02-0319-072 高阶交错网格有限差分算法
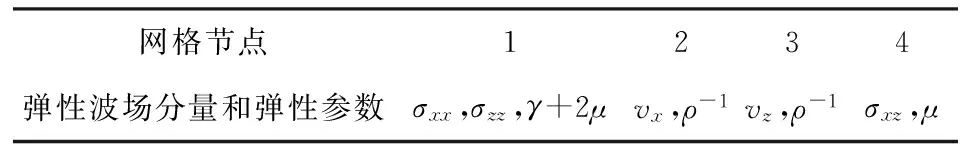
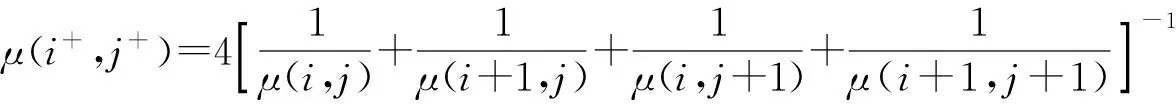
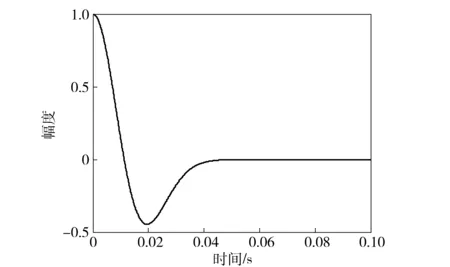
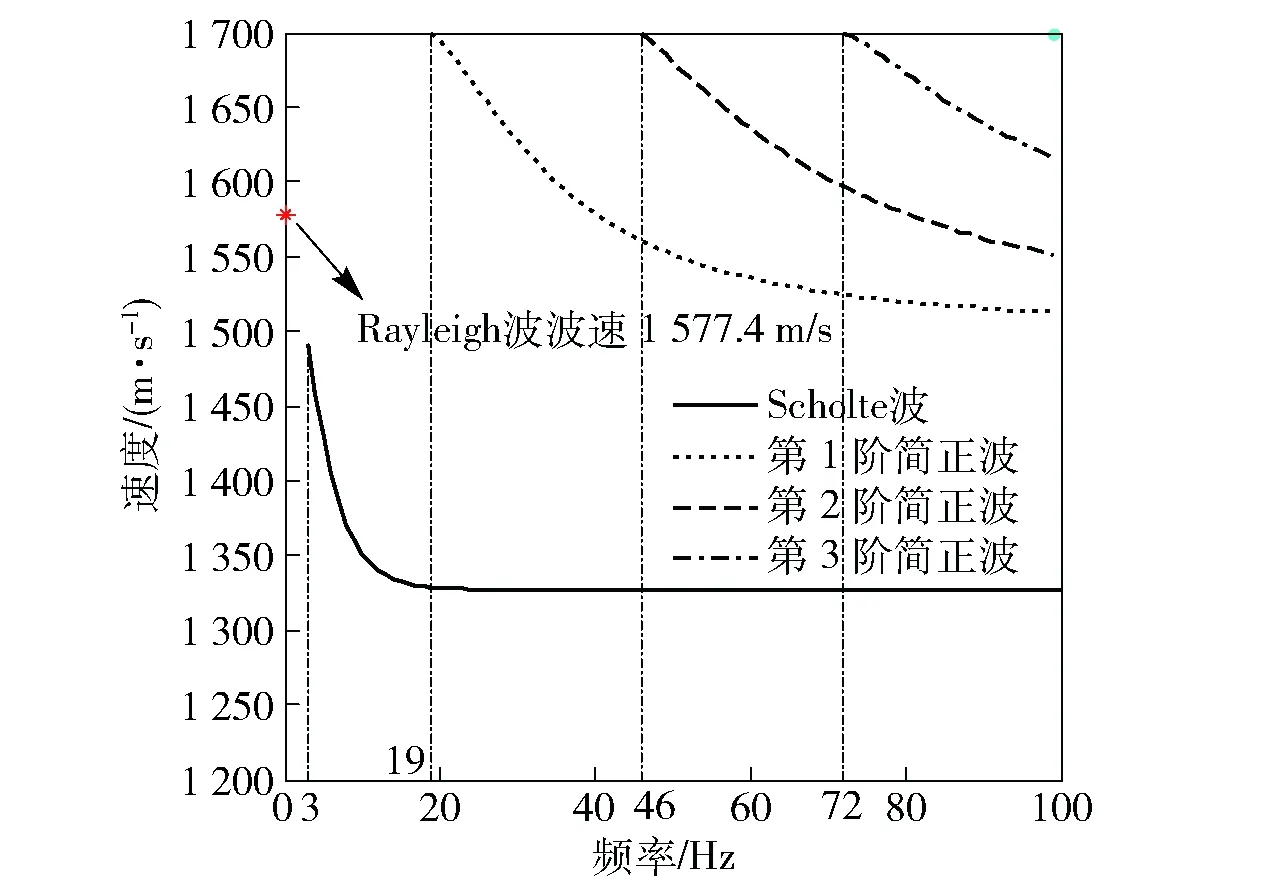
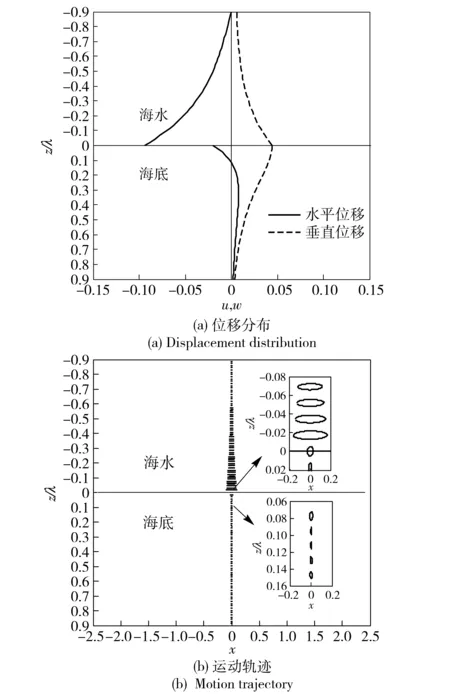
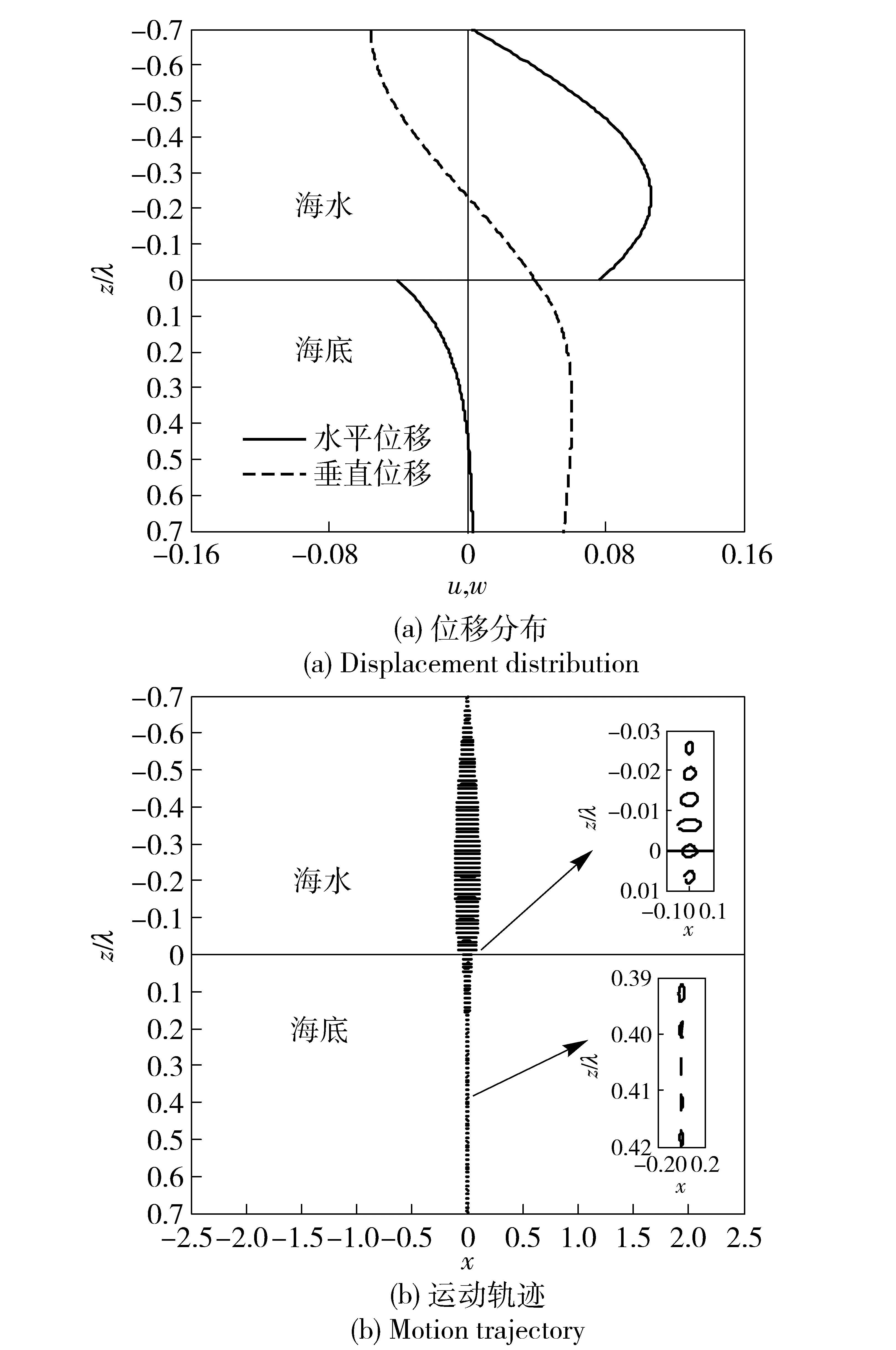
3 数值模拟及试验数据分析
4 结论

