Khatri-Rao积变换下的离格信号DOA估计*
李 根,梁玉英
(军械工程学院 电子与光学工程系,石家庄 050003)
Khatri-Rao积变换下的离格信号DOA估计*
李 根*,梁玉英
(军械工程学院 电子与光学工程系,石家庄 050003)
当存在离格信号时,基于稀疏表示的波达角(DOA)估计算法性能损失严重。为解决这个问题,在对接收数据协方差矩阵进行Khatri-Rao积变换的基础上,推导了离格信号网格偏离量与紧邻信号原子系数之间的关系,提出了一种单一离格信号DOA估计方法。为提高对邻近离格信号DOA的估计性能,利用矩阵的广义逆性质提出了基于多原子系数的联合估计方法。仿真实验表明,单一离格信号DOA估计方法在低信噪比下有较好的性能,联合估计方法在高信噪比条件下对邻近离格信号DOA有较高的估计精度,同时所提算法估计性能几乎不受网格划分间距的影响,可以通过增大网格间距降低算法运算量。相关研究对阵列天线DOA估计具有一定的参考价值。
离格信号;稀疏表示;DOA估计;Khatri-Rao积变换;压缩感知
1 引 言
信号波达角(Direction of Arrival,DOA)估计在雷达、声呐、无线通信、电子侦察等领域有着重要的应用。为了实现超分辨测向,多重信号分类法[1](Multiple Signal Classification,MUSIC)、旋转不变子空间法[2](Estimation of Signal Parameters via Rotational Invariance Technique,ESPRIT)等经典的子空间类算法被提出,但在快拍数不足或出现相干信源时,该类方法由于不能有效分离信号子空间和噪声子空间而导致估计性能严重下降。近年来,压缩感知由于突破了奈奎斯特采样定律,可以基于少量采样数据高精度的重建信号而受到广泛关注。压缩感知中的稀疏表示理论也被成功地应用到了阵列天线的DOA估计中[3],典型算法主要有基于L1范数凸松弛约束的L1-SVD[4]算法以及基于稀疏贝叶斯学习的BCS-DOA[5]算法。
在应用稀疏表示理论进行DOA估计之前,需要在角度域进行等间隔划分以构建精细的过完备字典,因此,这些基于稀疏表示的DOA估计算法只能估计位于过完备字典原子网格上的信号。当信号的DOA不位于网格上时(定义为离格信号),这类算法的估计精度将急剧下降。近年来,离格信号的稀疏重建得到了广泛的关注。文献[6]在对导向矢量进行泰勒分解的基础上提出了稀疏最小二乘(Sparse Total Least-Squares,STLS)的方法。文献[7]提出了一种交替下降最小二乘算法,该方法采用1范数和2范数的混合范数约束,具有较大的运算量,而且对于位于网格上的信号估计性能较差。文献[8]提出了模型误差下的稀疏谱拟合算法(Sparse Spectral Fitting with Modeling Uncertainty,SSFMU),该算法需要对联合稀疏优化的问题进行求解,有较大的运算量。文献[9-10]在泰勒分解基础上提出了基于贝叶斯推理的离格信号DOA估计方法。文献[11]提出了基于快速支持向量机的快速贝叶斯离格信号DOA估计算法,基于贝叶斯推理的算法在推理过程中采用了近似处理来降低运算量,在低信噪比下具有较好的估计性能,但在信源间隔较近、网格间距较大时估计性能下降明显,同时推理过程中的近似处理导致算法在信噪比较高的情况下仍存在一定的估计偏差。
为解决以上算法存在的问题,本文在稀疏表示理论下提出了一种建立在KR(Khatri-Rao)积变换[12]基础上,利用紧邻信号的两个原子系数来估计离格信号网格偏离量的方法,针对信号角度间隔较近时难以精确估计每个信号网格偏离量的问题,提出了基于多信号邻近原子系数的联合估计方法。为获取紧邻信号的原子系数,算法首先对接收数据协方差矩阵进行KR积变换,并基于l1范数约束对信号DOA进行稀疏重建从而找到紧邻信号的原子,然后对原子系数进行重建以提高其估计精度,最后根据推导出的原子系数与信号网格偏离量的关系实现对离格信号DOA的精确估计。
2 阵列信号模型
2.1 远场窄带信号模型
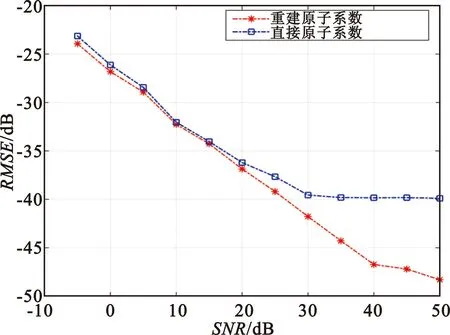
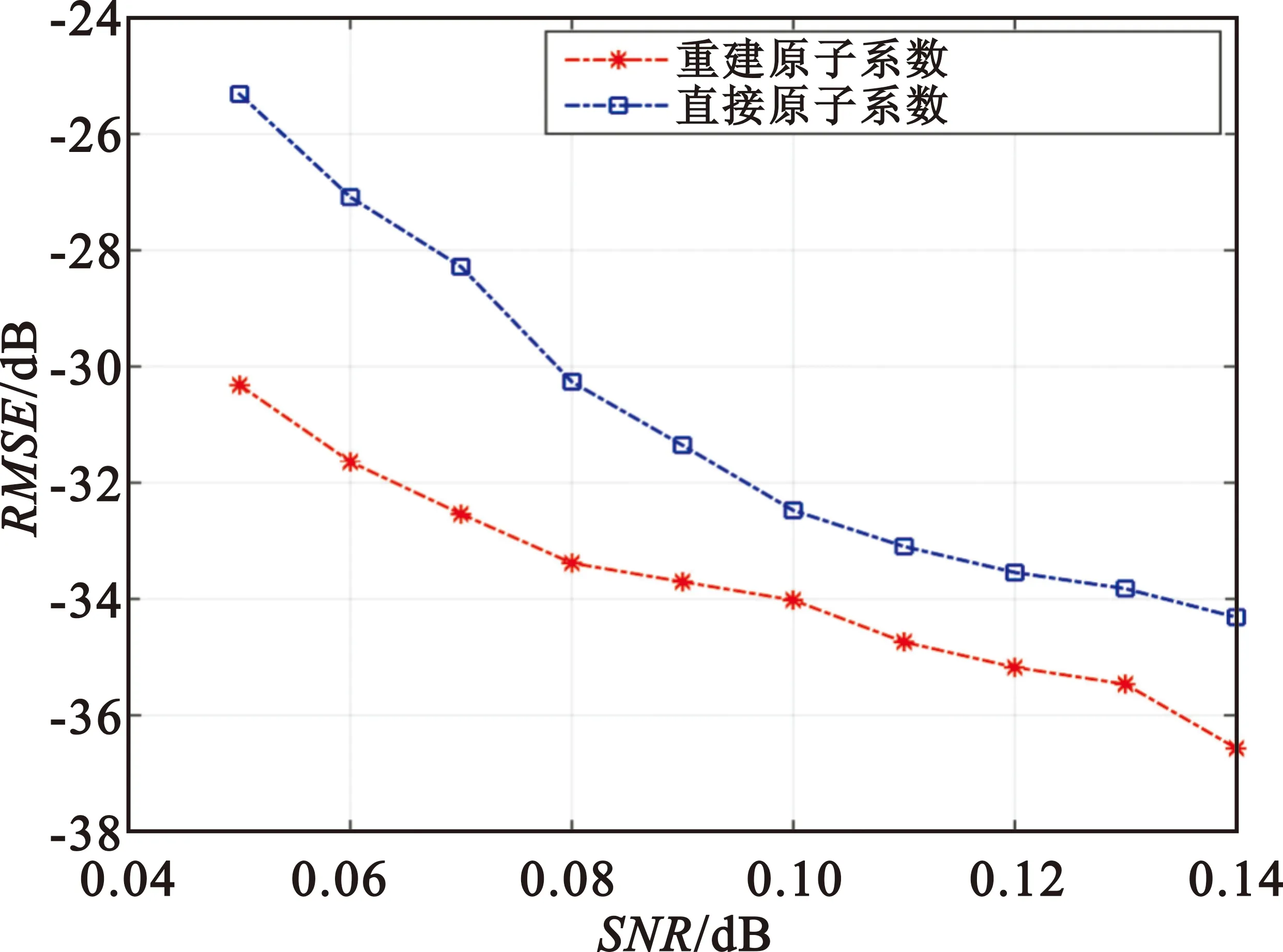
假设一个M元均匀线性阵列,阵元间距d=λ/2,有K(K x(t)=A(θ)s(t)+n(t),t=1,2,…,N。 (1) 式中:s(t)=[s1(t),s2(t),…,sK(t)]T;A(θ)=[a(θ1),a(θ2),…,a(θK)]∈M×K为阵列流型矩阵,a(θk)=[1 e…e]T为第k个信号的导向矢量;n(t)为加性高斯白噪声。 2.2 阵列协方差矩阵稀疏表示模型 进一步假设信号与噪声不相关,阵列的协方差矩阵可以表示为 (2) (3) 式中:⊙表示Khatri-Rao积,即 GB(θ)=A*(θ)⊙A(θ)= [a*(θ1)⊗a(θ1),…,a*(θK)⊗a(θK)] 。 (4) 式中:⊗表示Kronecker积;G∈(M2×(2M-1))为选择矩阵,表示为 (5) (6) 其中:B(θ)=[b(θ1),b(θ2),…,b(θK)]∈(2M-1)K,b(θk)为2M-1维的导向矢量,表示为 (7) 信号DOA的范围为θk∈[-90°,90°],对应在正弦空间的范围为uk∈[-1,1],其中uk=sinθk。将信号DOA在正弦空间[-1,1]上过完备化为一个网格{u1,u2,…,uQ}(Q≫M),则基于稀疏表示的DOA估计方法可以理解为从候选角度网格{u1,u2,…,uQ}上搜索真实DOA的过程。 如果真实DOA位于候选的角度网格上,则式(3)可以稀疏表示为 (8) 式中:GB(u)∈M2×Q为过完备字典,其每一列定义为过完备字典的原子,GB(u)的第k列(即称第k个原子)为a*(uk)⊗a(uk);r=[r1,r2,…,rQ]T为稀疏空间谱,r1,r2,…,rQ定义为依次对应字典中每一列(即每个原子)的原子系数,只有和真实信号DOA相匹配的原子其系数才不为0,因此当存在K个不同方向的入射信号时,r为K稀疏向量。入射信号波达角uk的估计问题可以转为对稀疏向量r的估计。令为r的估计值,根据稀疏重建理论,的估计可以转化为以下l1范数最小问题: (9) 2.3 信号波达角的稀疏重建 Δy~AsN(0M2,1,W) 。 (12) (13) 式中:Asχ2(M2)表示具有M2个自由度的渐近卡方分布。因此,式(9)的凸优化问题可以表示为 (14) 由于在网格上候选的方向是离散的,而真实信号的波达方向是连续分布的。当其不位于候选网格上时(即离格信号),此时用候选原子表示真实信号将存在偏差。下面给出离格信号DOA估计方法。 3.1 单一离格信号DOA估计 式(14)凸优化问题的物理意义是用最少的原子来表示入射信号,当信号DOA不在原子网格上时,式(14)的解是选择距离入射信号最近的原子来表示。下面给出一种在KR积变换稀疏重建基础上利用原子系数估计单一离格信源DOA的方法,记为KR-SR-Single算法。 离格信号可以表示为 (15)式中:cRes为不能由c(ul)、c(ul+1)两个原子表示的残差。c(ul)、c(ul+1)的系数α1和α2可通过下式获得: (16) (17) (18) 对于D(x),由于Q≫M,D(x)在区间[0,1]上近似成线性,即 (19) 式中:k0为线性斜率。根据式(17)~(19),可解得 (20) 因此,根据c(ul)、c(ul+1)两个原子的系数α1和α2可以估计出离格信号的网格偏离量ε,α1和α2的估计精度将直接影响ε的估计精度。 为排除原子的小分量干扰,在已知c(ul)、c(ul+1)的基础上,采用下式对α1和α2进行原子系数重建: (21) 3.2 多离格信号DOA估计 存在多入射信号时,信号DOA的间距越近,它们之间相互影响的程度越大。根据文献[14],当信号的空域角频率(阵元间距为半个波长时,空域角频率为πsinθ)间隔大于等于2π/M时,信号之间的相互影响可以忽略不计,2π/M也被称为M元阵列DOA分辨的“瑞利限”。本文构建字典原子时采用了KR积变换使阵元个数扩展到2M-1,因此,当信号的空域角频率间隔大于2π/(2M-1)时,采用KR-SR-Single算法估计每个信号的网格偏离量可以有较高的精度,当信号的空域角频率间隔小于瑞利限时,网格偏离量的估计将会产生较大偏差,下面提出一种基于多信号原子系数的联合估计方法,记为KR-SR-Joint算法。 (22) 通过数学化简,α1、α2、α3、α4满足 (23) (24) 因此,ε1和ε2可通过下式优化求解得到: (25) 3.3 算法复杂度和适用性分析 经典的L1-SVD[4]算法运用CVX凸优化工具箱进行重建每次迭代的运算量约为O(K3Q3),基于贝叶斯推理的离格信号DOA估计算法[9](Off-grid Direction of Arrival Estimation using Sparse Bayesian Inference,OGSBI)每次迭代的运算量为O(MQ2),本文所提的KR-SR-Single采用式(20)对信号网格偏离量进行估计,离格估计的运算量可忽略不计。KR-SR-Joint算法根据式(25)估计信号的网格偏离量,由于ε1和ε2的取值范围均为[0,1],因此式(25)的优化问题是容易解决的,其运算量远小于进行稀疏重建的运算量。因此本文所提KR-SR-Single和KR-SR-Joint两种算法的运算量主要在稀疏重建部分,KR积变换后协方差矩阵为一维向量,稀疏重建每次迭代的运算量约为O(Q3),不随信源数量的增加而增大,其运算复杂度远小于L1-SVD算法。 所提算法可以直接应用于非相关信源的DOA估计,当存在相关信源时,由于KR积变换时相关信源会产生耦合,需要先对相关信源采用空间平滑等方法进行解相关处理后才能用本文所提算法。 为全面分析比较算法性能,仿真时选用基于压缩感知的L1-SVD算法和OGSBI算法以及经典的MUSIC和ESPRIT算法进行对比,并引入了阵列天线波达角估计的克拉美罗界(CRB)来直观表明算法性能。所有仿真实验中,采用的阵型为均匀直线阵,阵元数为10,阵元间距为半个波长,噪声为0均值的高斯白噪声,正弦空间网格划分间距为0.01,离格信号数量为2且不相关,离格信号的DOA为正弦值,蒙特卡洛仿真的次数为300,用均方根误差(RMSE)衡量算法的估计性能。除仿真1外,本文所提的KR-SR-Single和KR-SR-Joint算法在对离格信号网格偏离量进行估计前分别根据式(21)和式(22)对原子系数进行了重建。 仿真1 原子系数估计精度对离格信号DOA估计性能的影响 快拍数为300,离格信号DOA分别为0.143和0.375,信噪比从-5 dB步进到50 dB,步进长度为5 dB。根据式(14)进行稀疏重建,由于离格信号的角度间隔较大,采用式(14)得到的直接原子系数和式(21)得到的重建原子系数使用式(20)对网格偏离系数进行估计,统计分析DOA估计的RMSE结果如图1(a)所示。固定信噪比为20 dB,信源的间隔从0.05步进到0.14,步进长度为0.01,其他条件不变,得到仿真分析结果如图1(b)所示。 (a)不同信噪比下估计性能分析 (b)不同角度间隔下估计性能分析图1 不同原子系数估计方法下的RMSE分析Fig.1 The analysis of RMSE under different atomic coefficient estimation methods 图1表明,单一离格信号DOA估计算法(KR-SR-Single)在高信噪比下存在固定偏差,这是由式(19)的近似线性表示导致的。可以看出,重建原子系数可以降低高信噪比下的固定偏差,同时当信号的波达角间隔较小时,重建原子系数对离格信号DOA的估计精度改善较为明显。 仿真2 大角度间隔离格信号和邻近离格信号DOA估计性能分析 为全面说明算法在不同信噪比下的估计性能,在大角度间隔离格信号和邻近离格信号两种背景下进行仿真分析。快拍数为300,两个大角度间隔的离格信号DOA分别为0.143和0.587,仿真时信噪比从-5 dB步进到51 dB,步进长度为4 dB;两个邻近的离格信号DOA为0.143和0.197,仿真时信噪比从10 dB步进到50 dB,步进长度为5 dB。统计分析本文所提的KR-SR-Single和KR-SR-Joint算法以及MUSIC、ESPRIT、 L1-SVD、OGSBI等算法在不同信噪比下DOA估计性能,仿真中同时加入了该仿真条件下的CRB,大角度间隔离格信号和邻近离格信号的DOA估计性能分别如图2和图3所示。 图2 大角度间隔下RMSE分析Fig.2 The analysis of RMSE under large angle interval 图3 邻近角度下的RMSE分析Fig.3 The analysis of RMSE under adjacent angle 图2表明,在快拍数为300,信源角度间隔较大时,MUSIC算法和ESPRIT算法均有较好的估计性能,同时MUSIC算法的估计性能要好于ESPRIT算法,但MUSIC算法进行DOA估计时仍需进行角度搜索,实现高精度的估计需要划分过密的角度网格,将带来较大的运算量。L1-SVD算法只能估计网格上的信号,高信噪比下对离格信号的估计有较大的固定偏差。OGSBI以及本文所提的KR-SR-Single和KR-SR-Joint算法均可以实现对离格信号的估计,在高信噪比下KR-SR-Single和OGSBI算法存在固定偏差,这是由于两种算法均采用了近似处理而导致的。在信噪比较低时KR-SR-Single算法的估计性能较好,KR-SR-Joint算法在信噪比较高的情况下,估计性能好于相比较的算法,逼近CRB曲线。 图3表明,当信源角度间隔较小,信噪比相对较小时,基于稀疏表示的算法估计性能均明显好于MUSIC和ESPRIT算法。但图3中信号空域角频率间隔为0.054π,而信号之间不产生相互干扰的临界空域角频率间隔为2π/(2M-1)=0.105π,因此图3中的邻近信号之间产生了相互干扰,导致KR-SR-Single算法在高信噪比下存在较大的固定估计偏差。KR-SR-Joint算法估计时考虑了信号之间相互影响,因此随着信噪比的增大逼近CRB曲线,具有较好的估计性能,但KR-SR-Joint算法更容易受到噪声的影响,在信噪比偏低的时候存在明显高于KR-SR-Single算法的估计误差。 仿真3 少快拍数和信号离格大小对DOA估计精度的影响分析 为表明所提算法在少快拍数下的估计性能,仿真时采用的快拍数为10,离格信号DOA分别为0.143和0.375,仿真时信噪比从0 dB步进到35 dB,步进长度为5 dB。统计分析本文所提的KR-SR-Single和KR-SR-Joint算法以及MUSIC、ESPRIT、 OGSBI、 L1-SVD等算法在不同信噪比下DOA估计性能,结果如图4所示。为表明信号离格大小(size of off-grid)对所提算法估计性能的影响,仿真时采用的快拍数为300,信噪比为15 dB,两个离格信号分别为0.14+ε和0.37+ε,ε从0.001步进到0.009,步进间隔为0.001,统计分析KR-SR-Single和KR-SR-Joint算法以及OGSBI、L1-SVD等算法在不同信噪比下DOA估计性能,结果如图5所示。 图4 少快拍数下的RMSE分析Fig.4 The analysis of RMSE under few snapshots 图5 不同离格大小下的RMSE分析Fig.5 The analysis of RMSE under different sizes of off-grid 图4表明,快拍数较小,信噪比较低时,MUSIC和ESPRIT等经典算法的估计能较差,而基于稀疏重建的KR-SR-Single、KR-SR-JointDOA、OGSBI、 L1-SVD 4种DOA估计算法有较好的估计性能。但由于快拍数较少,KR-SR-Single、KR-SR-Joint、OGSBI这3种离格信号DOA估计算法对噪声较为敏感,在高信噪比下都有固定的估计偏差,其中本文所提的KR-SR-Single算法的估计性能相对较好。图5表明,KR-SR-Single和KR-SR-Joint算法的估计性能几乎不受信号离格大小的影响,而L1-SVD不能估计离格信号,因此其估计精度随信号离格大小的增大而降低,同时从图中可以看出OGSBI算法的估计精度也受离格大小的影响。 仿真4 不同网格间距下离格信号DOA估计精度对比分析。 为表明网格划分间距(grid spacing)对算法性能的影响,对基于稀疏重建的KR-SR-Single、KR-SR-Joint、OGSBI、 L1-SVD 4种算法进行仿真分析。仿真时,过完备字典在正弦空间的网格间距Δdg从0.01步进到0.05,步长为0.01,信噪比固定为20 dB。为使信号在不同的网格间距下有相同的网格偏离量,设定每个网格间距下的离格信号DOA分别为0.3·Δdg和0.6+0.7·Δdg,得到仿真结果如图6所示。 图6 不同网格间距下RMSE分析Fig.6 The analysis of RMSE under different grid spacing 从图6中可以看出,随着网格间距增大,L1-SVD和OGSBI算法的估计精度明显变差,而本文所提的KR-SR-Single和KR-SR-Joint算法的估计精度基本保持不变,KR-SR-Single和KR-SR-Joint算法可以保证在粗网格划分下具有较高的估计精度,因此,本文算法可以通过降低网格划分密度来减少算法的运算量。 雷达对目标进行探测时,角度邻近的离格信号是普遍存在的,此时基于稀疏表示的DOA估计算法性能损失严重,为此本文提出了KR-SR-Singl算法和KR-SR-Joint算法,提高了不同信噪比下对角度邻近离格信号的估计精度。相较现有算法,所提算法基于KR积变换,在保证估计精度的同时降低了运算量,同时算法性能受网格划分间距的影响较小,可通过增大网格间距进一步降低运算量。然而,KR积变换只能用于非相关信号,下一步将继续研究基于KR积变换的相关离格信号估计方法。 [1] SCHMIDT R O. Multiple emitter location and signal parameters estimation[J].IEEE Transactions on Antennas and Propagation,1986,34(3):276-280. [2] ROY R,KAILATH T. ESPRIT-estimation of signal parameters via rotational invariance techniques[J].IEEE Transactions on Acoustics Speech and Signal Processing,1989,37(7):984-995. [3] 赵宏伟,刘波,谢广钱,等. 基于压缩感知的卫星干扰源定位[J].电讯技术,2015,55(5):467-471. ZHAO Hongwei,LIU Bo,XIE Guangqian,et al.Satellite interference localization based on compressive sensing theory[J].Telecommunication Engineering,2015,55(5):467-471.(in chinese) [4] MALIOUTOV D,MUJDAT C,WILLSKY A. A sparse signal reconstruction perspective for source localization with sensor arrays[J].IEEE Transactions on Signal Processing,2005,53(8):3010-3022. [5] CARLIN M,ROCCA P,OLIVERI G. Directions-of-arrival estimation through Bayesian compressive sensing strategies[J].IEEE Transactions on Antennas and Propagation,2013,61(7):3828-3838. [6] ZHU H,GEERT L,GEORGIOS B G. Sparsity-cognizant total least-squares for perturbed compressive sampling[J].IEEE Transactions on Signal Processing,2011,59(5):2002-2016. [7] ARIS G,MARK D. An alternating descent algorithm for the off-grid doa estimation proble with sparsity constraints[C]//Proceedings of 20th European Signal Processing Conference(EUSIPCO).Bucharest,Romania:IEEE,2012:874-878. [8] ZHENG J,KAVEH M. Directions-of-arrival estimation using a sparse spatial spectrum model with uncertainty[C]//Proceedings of 2011 IEEE International Conference on Acoustics,Speech,and Signal Processing.New York:IEEE,2011:2848-2851. [9] YANG Z,XIE L H,ZHANG C S. Off-grid direction of arrival estimation using sparse Bayesian inference[J].IEEE Transactions on Signal Processing,2013,61(1):38-43. [10] ZHANG Y,YE Z,XU X. Off-grid direction of arrival estimation based on weighted sparse Bayesian learning[C]//Proceedings of 2014 Fourth International Conference on Audio,Language and Image Processing.New York:IEEE,2014:547-550. [11] LIN J C,MA X C,YAN S F,et al. Off-grid fast relevance vector machine algorithm for direction of arrival estimation[J].IET Radar Sonar and Navigation,2016,10(4):718-725. [12] MA W K,HSIEH T H,CHI C Y. DOA estimation of quasi-stationary signals with less sensors than sources and unknown spatial noise covariance:a Khatri-Rao subspace approach[J].IEEE Transactions on Signal Processing,2010,58(4):2168-2180. [13] YIN J,CHEN T. Direction-of-arrival estimation using a sparse representation of array covariance vectors[J].IEEE Transactions on Signal Processing,2011,59(9):4489-4493. [14] CANDES E J,FERNANDEZ G C. Towards a mathematical theory of super-resolution[J].Communications on Pure and Applied Mathematics,2014,67(6):906-956. Off-Grid Signal DOA Estimation under Khatri-Rao Product Transform LI Gen,LIANG Yuying When the off-grid signals appear,the performance of direction-of-arrival(DOA) estimation algorithms based on sparse representation suffer serious loss. In order to solve this problem,the Khatri-Rao product transform is performed for covariance matrix of received data,the theoretical relationship between grid deviation and atomic coefficients close to the off-grid signal is derived,and then a method of single off-grid signal DOA estimation is proposed. For improving the DOA estimation performance of off-grid signals with approaching angles,a joint estimation method based on the multiple atomic coefficients is proposed by utilizing the generalized inverses properties.The simulation experiments show that the single off-grid signal DOA estimation method has excellent performance under low signal-to-noise ratio(SNR) and the joint estimation method has better performance facing the adjacent off-grid signal under high SNR.At the same time,the grid spacing has few influences on the estimation performance of the proposed algorithm.So enlarging the grid spacing can decrease the calculation amount of the proposed algorithm. These studies have certain reference value for DOA estimation of array antenna. off-grid signal;sparse representation;DOA estimation;Khatri-Rao product transform;compressive sensing 2016-06-03; 2016-09-13 Received date:2016-06-03;Revised date:2016-09-13 国防预研基金项目 10.3969/j.issn.1001-893x.2017.02.014 李根,梁玉英.Khatri-Rao积变换下的离格信号DOA估计[J].电讯技术,2017,57(2):203-209.[LI Gen,LIANG Yuying.Off-grid signal DOA estimation under Khatri-Rao product transform[J].Telecommunication Engineering,2017,57(2):203-209.] TN911.7 A 1001-893X(2017)02-0203-07 李 根(1991—),男,山东枣庄人,硕士研究生,主要研究方向为雷达信号处理; Email:307708608@qq.com 梁玉英(1968—),女,河北石家庄人,副教授、硕士生导师,主要研究方向为雷达信号处理。 *通信作者:307708608@qq.com Corresponding author:307708608@qq.com



3 离格信号估计方法


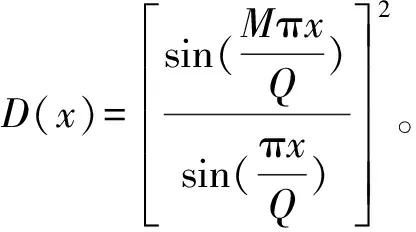


4 仿真分析





5 结束语
(Department of Electronic and Optical Engineering,Ordnance Engineering College,Shijiazhuang 050003,China)

