基于迭代列消元法的线性分组码参数盲识别*

王俊霞，张天骐，强幸子

(重庆邮电大学 信号与信息处理重庆市重点实验室，重庆 400065)

基于迭代列消元法的线性分组码参数盲识别*

王俊霞*，张天骐，强幸子

(重庆邮电大学 信号与信息处理重庆市重点实验室，重庆 400065)

针对线性分组码参数盲识别容错性能差的问题，提出基于迭代列消元法的线性分组码参数盲识别方法。首先对截获矩阵应用迭代列消元法，将其相关列对应各个窗内的转移矩阵中的列向量作为候选校验向量，再根据截获矩阵对偶码空间归一化维数来识别码字长度和同步时刻，最后将对偶码字进行初等行变换识别校验矩阵。仿真结果证明，与以往盲识别方法相比，所提方法容错性能好，适用于各种码率的线性分组码的码字长度、同步时刻和生成多项式识别。

非合作通信；线性分组码；盲识别；迭代列消元法

1 引 言

信道编码的盲识别是非合作信号处理领域的一个新的研究方向，在智能通信、信息对抗和信息截获领域有着广泛应用[1]。通常在数字通信系统中采用信道编码技术提高数据传输的可靠性[2]。因为线性分组码有简单的编、译码结构以及较好的纠错性能[3]，所以，在非合作通信中，如何根据截获序列识别线性分组码参数有非常重要的意义。

从公开发表的文献来看，线性分组码参数盲识别的方法主要有秩准则法[4]、对偶码空间法[5-6]、码重分析法[7]、高斯列消元法[8-9]等。秩准则法计算量小，但是容错性能很差。对偶码空间法容错性能好，但是计算量与码长指数倍成正比，并且对计算机内存要求很高，其门限仅适合中短码。码重分析法和关联规则法仅适用于低码率线性分组码。高斯列消元法容错性能有待进一步提高。

针对以上线性分组码盲识别存在的问题，本文采用迭代列消元法算法，对线性分组码参数进行了有效的识别。针对矩阵进行高斯列消元法时错误码元传播影响大的问题，文中采用迭代高斯列消元法，使错误码元仅仅在窗内传播，而不会影响窗外码元，使错误码元的传播范围大大减小。文中识别相关列时，并非根据秩准则的全零列，而是根据相关列、独立列中的0的比例减去1的比例统计特性不同，使得容错率进一步提高。相比文献[6]中的Walsh-Hadamard变换算法，其候选校验向量为2n个，本文中候选校验向量为迭代列消元法后的截获矩阵的相关列对应各个窗的转移矩阵中的列向量，候选校验向量的数目大大减少。此外，根据对偶码字、随机码字以及相关列、独立列的0的比例减去1的比例统计特性不同，文中提出了有效的判决门限，实现了在较高误码率情况下线性分组码参数盲识别。

2 线性分组码的概念与性质

定义1[10]将k位信息位分为一组进行独立处理，变为长度为n(n>k)位的码字，校验位长为n-k位，若校验位是信息位的线性组合，则称该编码为(n,k)线性分组码。

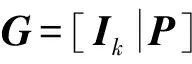
3 基于迭代列消元法的线性分组码参数盲识别原理

3.1 数学模型

假设发送端码字是(n0,k0)线性分组码，经过二进制对称信道传输，截获的二进制比特流为X。非合作方需要估计出线性分组码的参数，如码字长度、同步时刻t0及校验矩阵。

假设线性分组码码字长度是n，同步时刻是d，则将X前面d个比特截断，以码字长度n分为N个码字Xi,i=1,2,…,N，N=⎣(L-d)/n」，⎣」是取整符号，并且将每个码字构成截获矩阵X(n,d)的一行。

定义H(n,d)表示X(n,d)对应的所有校验向量张成的对偶码空间，dim表示求空间维数的运算，则根据文献[6]，满足

(1)

式中：α∈+。由式(1)可知，真实码字长度和同步时刻(n0,t0)对应的对偶码空间归一化维数最大，所以为了求对偶码空间维数，需要求对偶码空间内的校验向量。

3.2 门限的取值

当截获矩阵为X(n0,t0)时，截获矩阵的每一行都是由线性分组码码字c经过误码率为τ的二进制对称信道产生的码字x，则xhT=(c+e)hT=ehT。设无误码X(n0,t0)的校验向量空间为{hr}，其余向量为{hw}，根据文献[5]，如果h∈{hr}，则有

P(xhT=1)=0.5[1-(1-2τ)ωt(h)]，

(2)

P(xhT=0)=0.5[1+(1-2τ)ωt(h)] 。

(3)

式中：ωt(h)表示h的码字重量。

如果h∈{hw}，则有

P(xhT=1)=0.5，

(4)

P(xhT=0)=0.5 。

(5)

对于大小为N×n的截获矩阵X(n0,t0)，Xi表示X的第i行，则X(n,d)hT中0的比例减去1的比例为

(6)

定义y～(a,σ2)表示y服从均值为a、方差为σ2的正态分布，如果h∈{hr}，则

Z～(2P0-1,4P0(1-P0)/N) 。

(7)

式中：P0=0.5[1+(1-2τ)ωt(h)]。

如果h∈{hw}，则

Z～(0,1/N)。

(8)

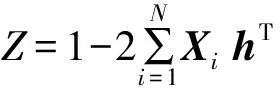
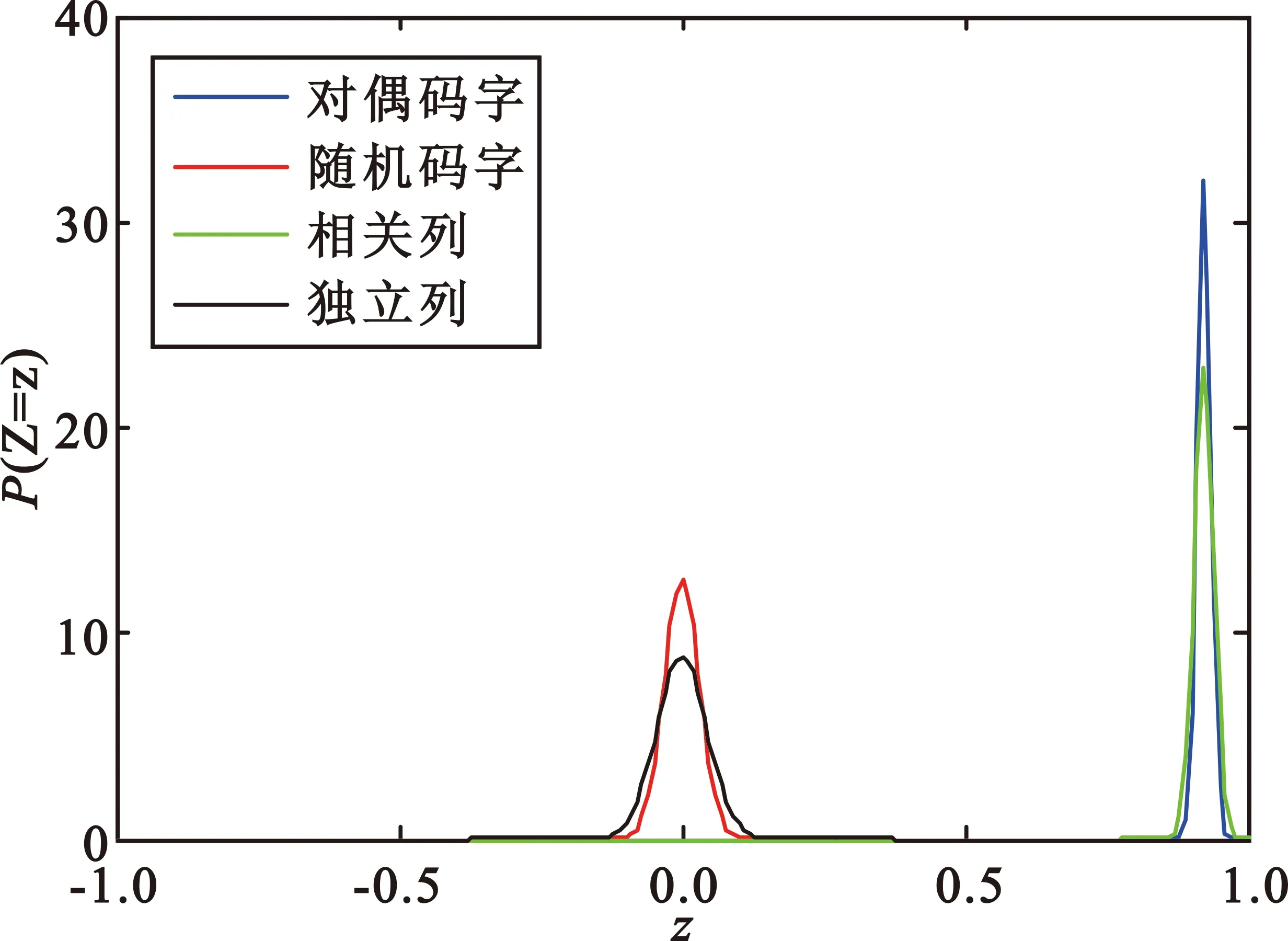
图1 对偶码字、随机码字、相关列及独立列对应的Z的概率分布图Fig.1 The corresponding Z′s probability distribution of dual code,random code,dependent column and independent column

3.3 迭代列消元法

文献[8]提出的高斯列消元法，由于其错误码元的传播范围大，文中提出的迭代列消元法设置窗，在窗内分别进行高斯列消元法，使错误码元仅在窗内传播。

迭代列消元法的步骤：

Step 1 假设截获矩阵X大小是N×n，X中的第i行、j列元素记作Xij，XN×n的第i行记作Xi=(Xi1Xi2…Xin)，若选取窗W的大小是m×n，则迭代次数是c=⎣N/m」。

Step 2 将窗W1放在截获矩阵XN×n的前m行，选取的矩阵为L(1)=(X1X2…Xm)Τ，若M(1)表示对L(1)高斯列消元后的行阶梯矩阵，则有M(1)=L(1)A(1)，其中，A(1)记录对L(1)进行高斯列消元法后的结果。

Step 3 依次迭代，每一次迭代都将窗Wt向下滑动m行，并且对窗内矩阵L(t)=(Xm(t-1)+1Xm(t-1)+2…Xmt)Τ高斯列消元化为行阶梯矩阵，则有M(t)=L(t)A(t)，t=1,2，…,c。

Step 4 记录迭代列消元法后的矩阵M=(M(1)M(2)…M(c))Τ和转移矩阵A=(A(1)A(2)…A(c))Τ。

文中算法W取值为2n×n，原因一为滑动窗所选取的矩阵，每一行为一个完整码字，窗内包含k维码字；原因二为W的行取值越小，错误码元的传播范围越小。

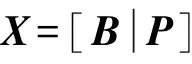
(9)

式中：1≤j≤n0-k0，α(j,m)∈{0,1}。若α(j,m)=1，则Pj与bm相关；若α(j,m)=0，则Pj与bm无关。对无误码矩阵X(n0,t0)进行迭代列消元法后，相关列Pj(1≤j≤n0-k0)可化为全零列，且转移矩阵为

(10)

式(10)右侧区域的列向量是相关列对应的第i个窗的列向量，是校验向量，并且互不相关，其作为对偶码空间的基向量，张成X(n0,t0)的n0-k0维对偶码空间。

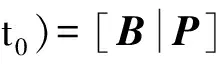
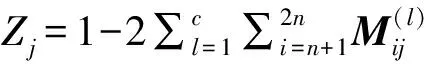
在迭代列消元法中，窗Wi(第i次迭代)中的错误不会传递到窗Wi+1(第i+1次迭代)，因为高斯列消元法在不同的窗内分别进行，所以错误码元只在小矩阵窗内传递，而不会影响其他窗内码字。在无误码的情况下，相关列对应的各个窗的转移矩阵的列向量为校验向量；在有误码的情况下，整个截获矩阵的相关列对应各个窗的转移矩阵的列向量可能为校验向量，也可能是非校验向量，如果迭代次数c足够大，整个截获矩阵的相关列对应各个窗的转移矩阵的列向量会包含所有的校验向量。本文中将整个截获矩阵的相关列对应各个窗的转移矩阵的列向量作为候选校验向量，然后再根据截获矩阵与校验向量、非校验向量乘积得到的向量中0的比例减去1的比例的统计特性不同，识别出校验向量。

本文算法具体步骤如下：

输入：长度为L的截获序列X，选取码字长度的最小值nmin=3和最大值nmax=2n0-1。

步骤1 初始化码字长度n=nmin，d=0，候选校验向量H1=φ。

步骤2 按照3.1节对每一种假设(n,d)构造大小为N×n的截获矩阵X(n,d)=(X1X2…XN)Τ，Xi表示X(n,d)的第i行。取m=2n，对X(n,d)进行迭代列消元法，可以得到迭代列消元法后的矩阵M=(M(1)M(2)…M(c))T和转移矩阵A=(A(1)A(2)…A(c))Τ。

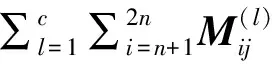
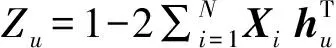
步骤5 求出每一种假设(n,d)下的对偶码空间归一化维数dim(H3)/n，并且放入向量S中。

4 仿真验证

截获序列为发送端为BCH(7,4)，二进制对称信道的误码率τ=0.01，截获时的同步时刻t0=3。已知其编码方式为线性分组码，用本文算法对截获序列进行盲识别，选取的参数均为N=1 000，T1=0.25，T2=0.5。

图2所示是采用本文算法对以不同码字长度和同步时刻构成的截获矩阵识别，求得其对应的对偶码空间归一化维数的仿真结果。当n=7、d=3时对偶码空间归一化维数最大，等于3/7，即对偶码空间维数为3，此时得到的对偶码空间基向量恰巧为BCH(7,4)的对偶码空间基向量。当n=7时，在d=3附近，对偶码空间维数大于0，小于3/7。当n≠7时，对偶码空间维数等于零，与先前理论分析一致。

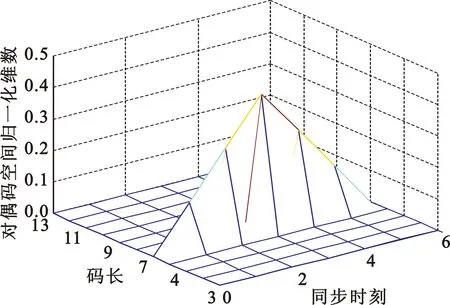
图2 对偶码空间归一化维数Fig.2 The normalized dual space dimension

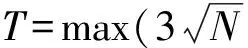
(a)本文算法

(b) Walsh-Hadamard算法图3 采用本文算法和Walsh-Hadamard算法对BCH(7,4)的仿真结果Fig.3 Simulation results of the proposed algorithm and Walsh-Hadamard algorithm

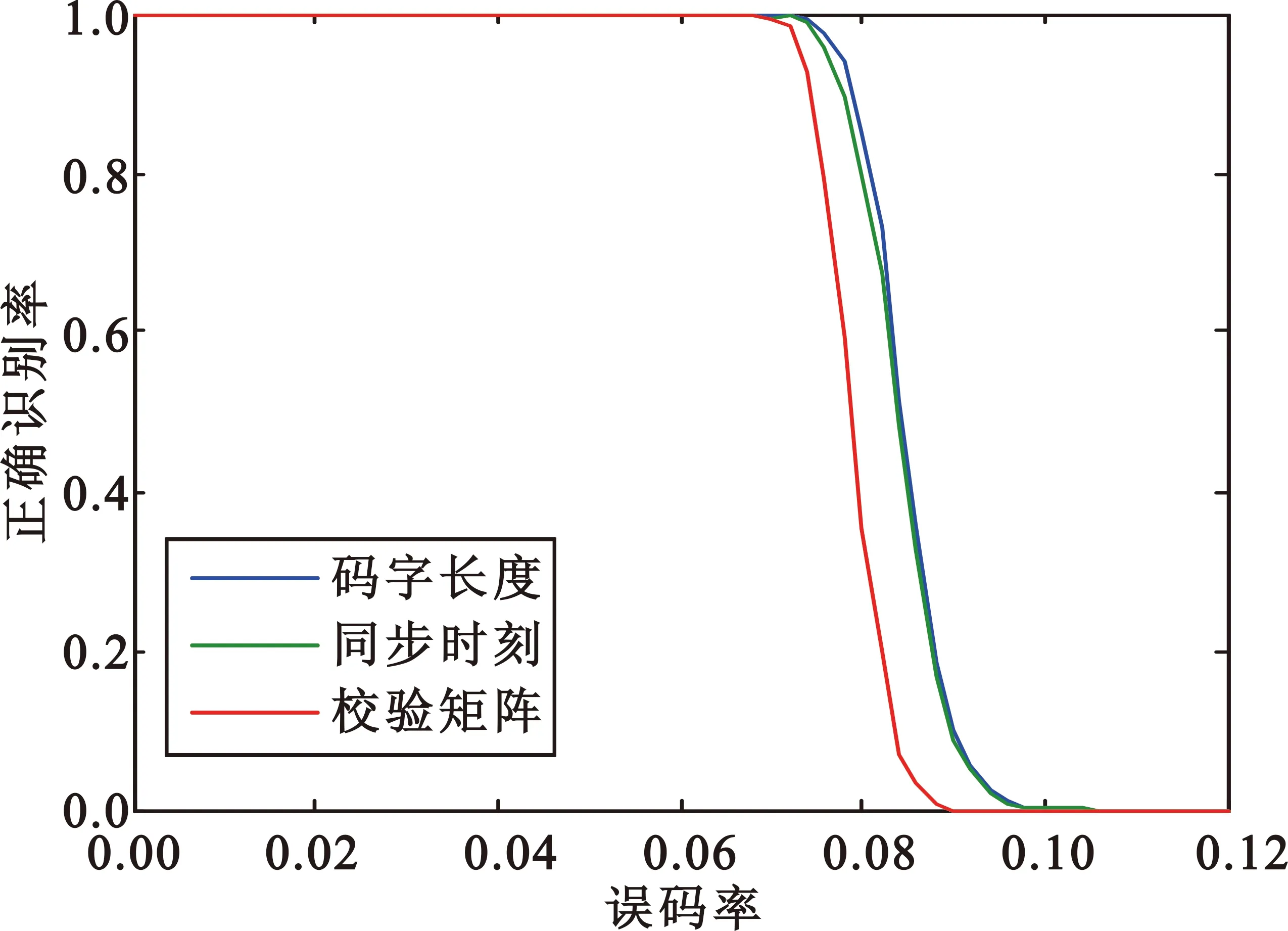
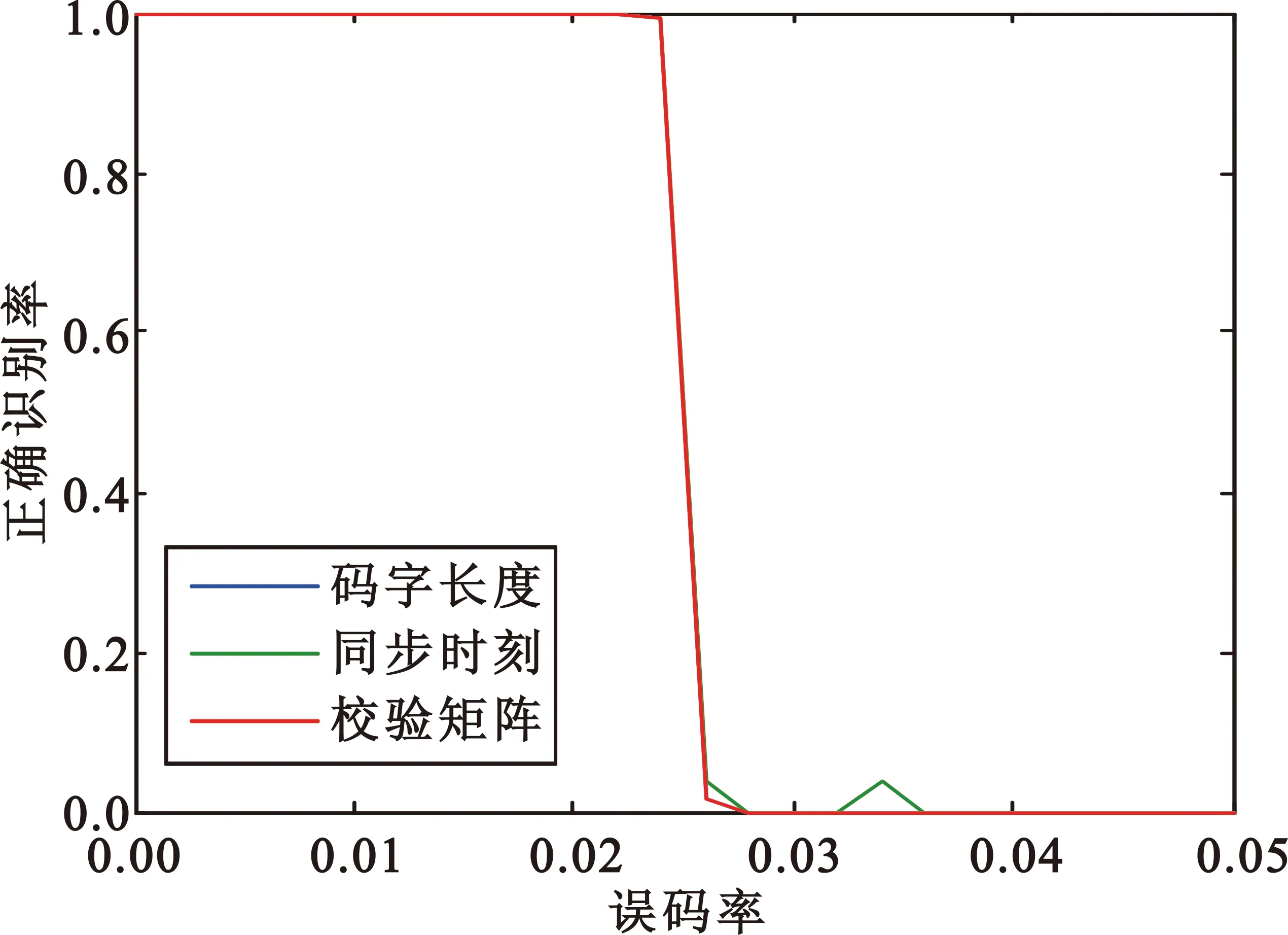
图4(a)是采用本文算法对BCH(15,7)，误码率0～0.1，步长为0.002进行500次蒙特卡洛的仿真结果。图4(b)是采用本文算法对BCH(15,11)，误码率0～0.05，步长为0.002进行500次蒙特卡洛的仿真结果。图4(c)是采用本文算法对BCH(63,16)误码率0～0.04，步长为0.002进行50次蒙特卡洛的仿真结果。图4(d)是采用本文算法对BCH(127,36)误码率0～0.02，步长为0.002进行10次蒙特卡洛的仿真结果。仿真结果表明，BCH(15,7)在误码率为0.052时，码字长度、同步时刻、校验矩阵的正确识别率仍能达到90%以上；BCH(63,16)在误码率为0.022时，码字长度、同步时刻、校验矩阵的正确识别率能仍能达到80%以上；BCH(127,36)在误码率为0.01时，码字长度、同步时刻正确识别率仍能达到80%以上。本文算法能够对各种码长和码率的码字进行有效识别，对低码率的识别效果更好，而且码率越高，码字长度、同步时刻、校验矩阵正确识别率越接近。

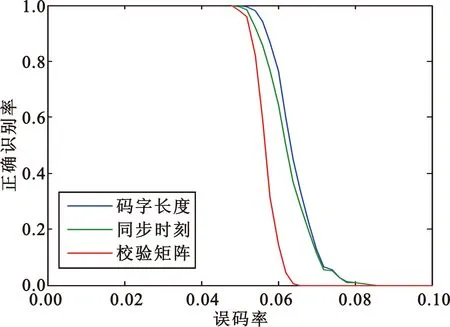
(a)BCH(15,7)

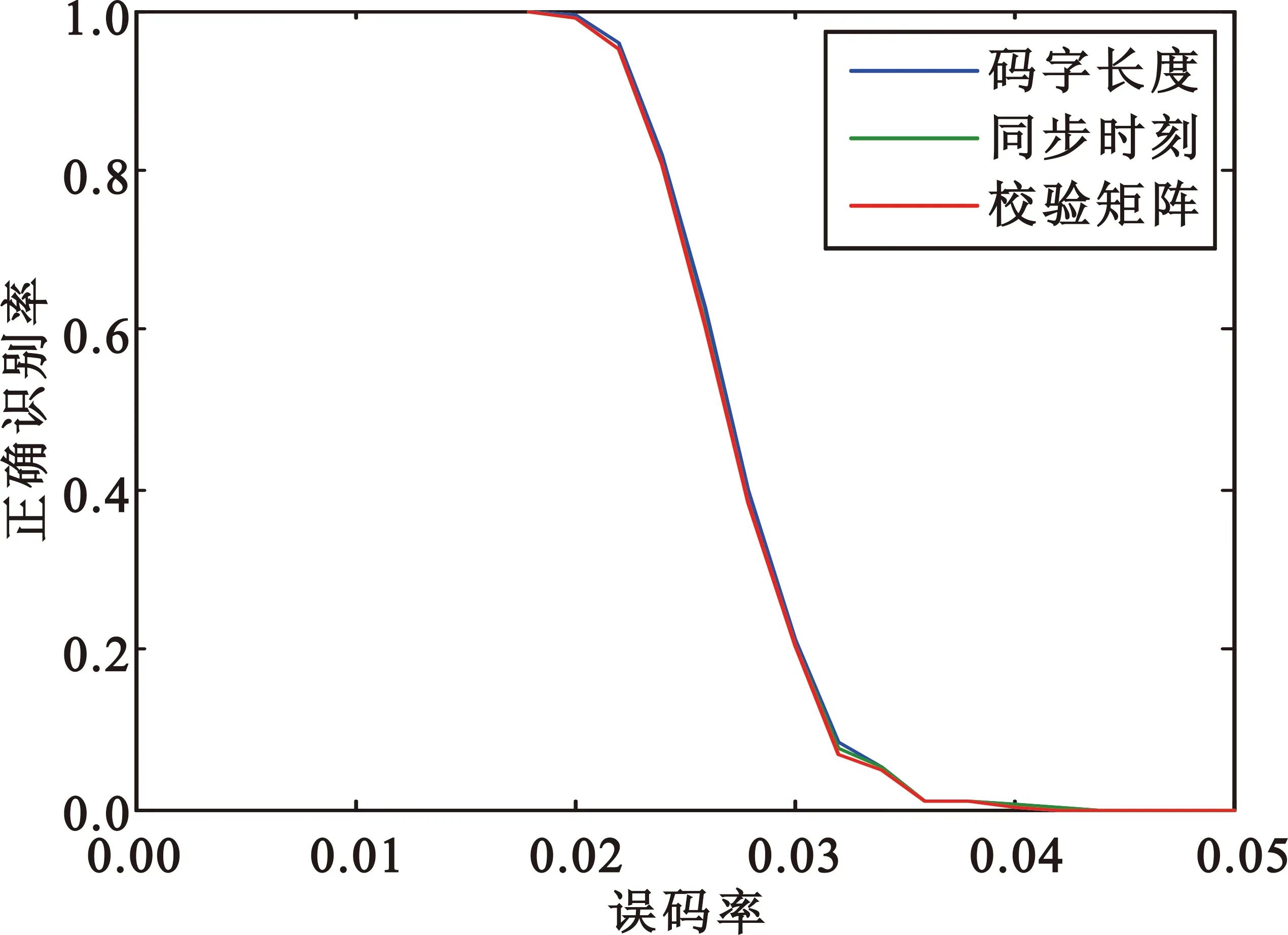
(b)BCH(15,11)

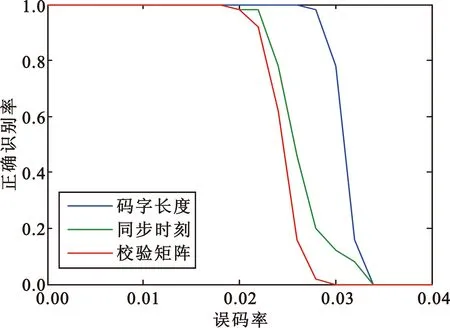
(c)BCH(63,16)

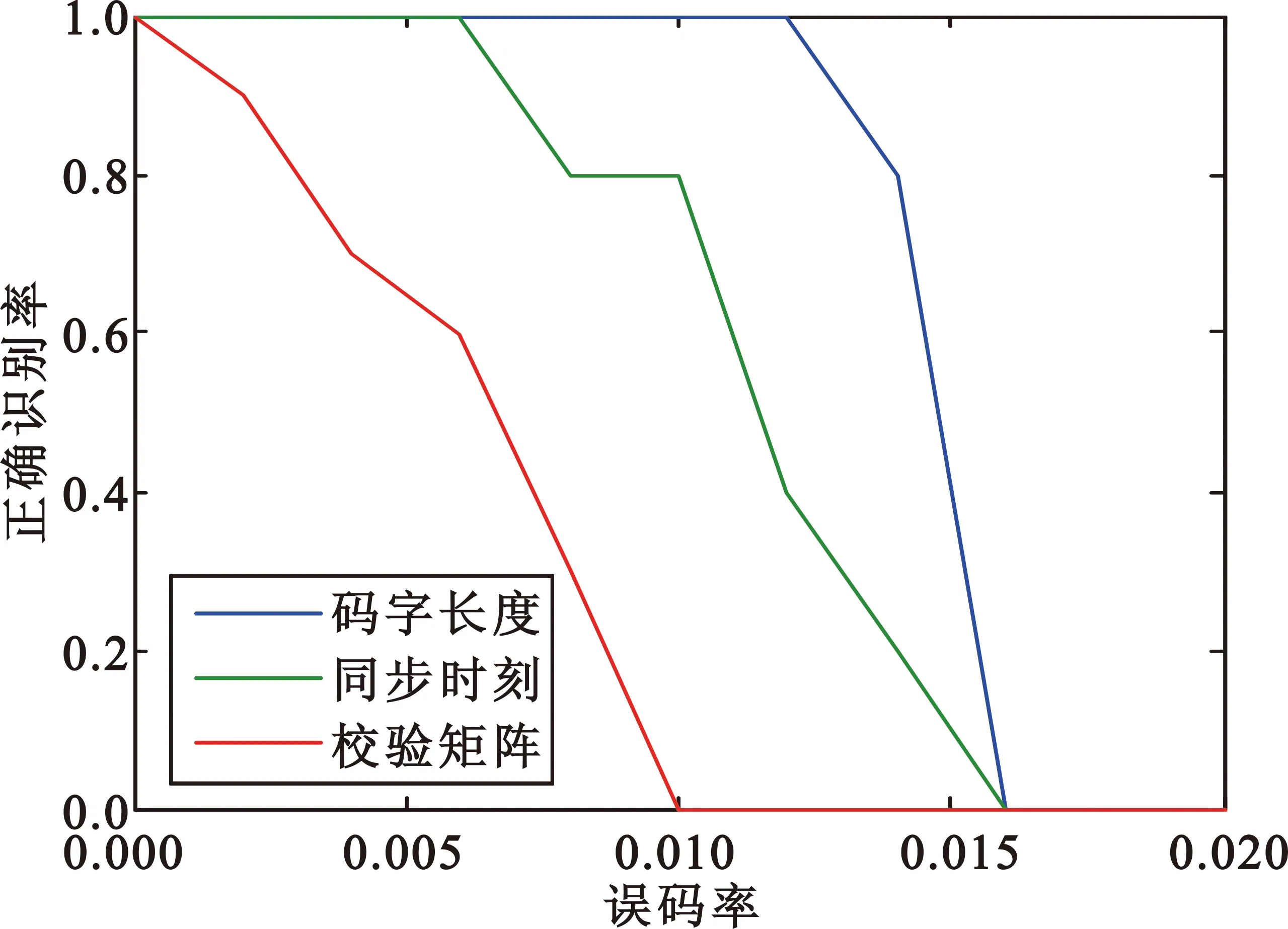
(d)BCH(127,36)图4 采用本文算法对不同线性分组码识别的仿真结果Fig.4 Simulation results of the proposed algorithm

5 结束语

本文算法将迭代列消元法后的截获矩阵的相关列对应各个窗内的转移矩阵的列向量作为候选校验向量，相比Walsh-Hadamard算法，候选校验向量数目大大较少，且不受计算机内存的限制，从而能够识别码长较长的线性分组码。在仅仅已知编码方式是线性分组码的情况下，采用本文算法对其多种线性分组码进行识别，有较好的容错性能。此外，本文算法根据对偶码字、随机码字、独立列和相关列的0的比例减去1的比例统计特性差异，提出了有效的判决门限，具有一定的工程应用价值。下一步希望研究一种计算复杂小且对高码率线性分组码参数有较好识别效果的算法。

[1] 解辉,黄知涛,王丰华. 信道编码盲识别技术研究进展[J].电子学报,2013，41(6):1166-1176. XIE Hui,HUANG Zhitao,WANG Fenghua. Research progress of blind recognition of channel coding[J].Electronica Sinica Acta,2013，41(6):1166-1176.(in Chinese)

[2] 闫郁翰. 信道编码盲识别技术研究[D].西安：西安电子科技大学,2012. YAN Yuhan. Study on blind recognition of channel coding[D].Xi′an:Xidian University,2012.(in Chinese)

[3] FENG G L,TZENG K K. A new procedure for decoding cyclic and BCH codes up to actual minimum distance[J].IEEE Transactions on Information Theory,1994,40(5):1364-1374.

[4] PLANQUETTE G. identification of binary code streams[D] .Rennes,France:University of Rennes I,1996.

[5] VALEMBOIS A. Detection and recognition of a binary linear code[J].Discrete Applied Mathematics,2001,111(1/2):199-218.

[6] 杨晓炜,甘露. 基于Walsh-Hadamard变换的线性分组码参数盲估计算法[J].电子与信息学报,2012,34(7):1642-1646.

YANG Xiaowei,GAN Lu. Blind estimation algorithm of the linear block codes parameters based on WHT[J].Journal of Electronics & Information Technology,2012,34(7):1642-1646.(in Chinese)

[7] 王兰勋,佟婧丽,孟祥雅. 一种线性分组码参数的盲识别方法[J].电视技术,2014,38(9):188-192. WANG Lanxun,TONG Jingli,MENG Xiangya. Blind recognition method of linear block codes parameters[J].Video Engineering,2014,38(9):188-192.(in Chinese)

[8] 李灿,张天骐,刘瑜. 基于伽罗华域高斯列消元法的RS码盲识别[J].电讯技术,2014，54(7):926-931. LI Can,ZHANG Tianqi,LIU Yu. Blind recognition of RS codes based on Golois Field columns Gaussian elimination[J].Telecommunication Engineering,2014，54(7):926-931.(in Chinese)

[9] 张天骐,易琛,张刚. 基于高斯列消元法的线性分组码参数盲识别[J].系统工程与电子技术,2013,35(7):1514-1519. ZHANG Tianqi,YI Chen,ZHANG Gang.Blind identification of parameters of linear block codes based on columns Gaussian elimation[J].Systems Engineering and Electronics,2013,35(7):1514-1519.(in Chinese)

[10] LIN S,COSTELLO D J. Error control coding[M].2nd ed. New Jersey,USA:Prentice Hall,2005:67-95.

[11] SICOT G,HOUCKES,BARBIER J. Blind detection of interleaver parameters[J].Signal Processing,2009,89(4):450-462.

Blind Recognition of Linear Block Code Parameters Based on Iterative Column Elimination Algorithm

WANG Junxia,ZHANG Tianqi，QIANG Xingzi
(Chongqing Key Laboratory of Signal and Information Processing,Chongqing University of Posts and Telecommunications,Chongqing 400065,China)

To improve the fault tolerance performance of blind identification of linear block code parameters,an iterative column elimination algorithm is proposed. First,the iterative column elimination algorithm is applied in the intercept matrix,and then the corresponding column in the transition matrix of a dependent column is placed in candidate parity-check matrix. In addition,the codeword length and synchronization are estimated when the normalized dual space dimension reaches the maximum. Finally,check matrix is estimated through elementary row transformation of dual code. The simulation results show that compared with previous blind identification method,the proposed method has good fault tolerance,and can recognize codeword length,synchronization and generator polynomial for linear block codes with different rate.

non-cooperative communication;linear block code;blind recognition;iterative column elimination algorithm

2016-05-17；

2016-08-03 Received date:2016-05-17；Revised date：2016-08-03

国家自然科学基金资助项目(61671095，61371164，61275099)；重庆市教育委员会科研项目(KJ130524,KJ1600427,KJ1600429);信号与信息处理重庆市市级重点实验室建设项目(CSTC2009CA2003)

10.3969/j.issn.1001-893x.2017.02.013

王俊霞，张天骐，强幸子.基于迭代列消元法的线性分组码参数盲识别[J].电讯技术，2017,57(2):197-202.[WANG Junxia,ZHANG Tianqi，QIANG Xingzi.Blind recognition of linear block code parameters based on iterative column elimination algorithm[J].Telecommunication Engineering,2017,57(2):197-202.]

TN911.22

A

1001-893X(2017)02-0197-06

王俊霞(1992—)，女，河南焦作人，硕士研究生，主要研究方向为信道编码参数的盲识别；

Email:1552268578@qq.com

张天骐(1971—)，男，四川眉山人，博士，教授，主要研究方向为语音信号处理、通信信号的调制解调、盲处理、神经网络实现以及FPGA、VLSI实现;

强幸子(1986—)，男，陕西咸阳人，硕士研究生，主要研究方向为通信信号处理。

*通信作者：1552268578@qq.com Corresponding author：1552268578@qq.com