拖曳式雷达诱饵目标识别技术*

肖 晶，王 虹，李跃华，张光锋

(南京理工大学 电子工程与光电技术学院，南京 210094)

拖曳式雷达诱饵目标识别技术*

肖 晶*，王 虹，李跃华，张光锋

(南京理工大学 电子工程与光电技术学院，南京 210094)

针对拖曳式雷达诱饵易对雷达导引头造成欺骗性干扰的问题，利用雷达回波中提取的目标微动多普勒特征、极化特征和雷达截面积序列统计特征进行仿真分析，在实现载机和诱饵初步识别的基础上，采用贝叶斯(Bayes)数据融合方法，对上述3种回波信号特征进行一级融合，并进一步对不同时刻的信号特征进行二级融合，最终将目标识别率由71.5%提高到了96%。该目标识别方法能够大大减少外界因素的影响，相对于单特征识别显著提高了目标识别率。

拖曳式雷达诱饵；目标识别；雷达导引头；欺骗干扰；贝叶斯数据融合

1 引 言

拖曳式雷达诱饵(Towed Radar Decoy,TRD)通过拖曳线与载机配置在一起，在转发方式下将接收到的雷达探测信号经放大后直接转发出去，该信号处于雷达的瞬时波束范围内，在角度上有效地欺骗单脉冲雷达[1]。TRD由载机拖着飞行，飞行速度与载机相同，而且诱饵与载机共处于雷达的半波束宽度内，因此雷达无法在速度和角度上对载机和拖曳式诱饵进行分选[2-3]。

由于诱饵与载机回波信号间存在一定的时间延迟，目前可采用目标前沿切割法进行分选，但脉冲切割宽度的合理选取存在一定难度。拖曳式雷达诱饵对光学探测系统不起作用，光学跟踪方法也是对抗拖曳式诱饵的一种选择，但该方法受天气状况限制，不能全天候工作[4-6]。

文献[7]提出通过Radon-Wigner变换，将回波信号从时域变换为由调频率和频率构成的参数空间域，在多普勒维上实现目标和诱饵的分离。文献[8]利用诱饵与目标的极化特征差异，提出一种基于自适应恒虚警阈值的双极化目标识别方法，但是由于只利用了单一的极化特征，在受到各种杂波干扰实战场景下识别率会大大下降[8-9]。

本文针对单一特征识别识别率不高的缺点，提出对雷达回波信号中的微动多普勒特征、极化特征和雷达截面积(Radar Cross Section,RCS)序列统计特征进行特征提取后再进行两级贝叶斯(Bayes)数据融合，进而提高目标识别率。通过两级Bayes融合，目标识别率由71.5%提高到96%，有效降低了虚警，提高了对载机和拖曳式雷达诱饵的目标识别能力。

2 目标特征提取

2.1 目标微多普勒特征提取

微动是目标或目标部件除质心平动以外的旋转、振动、翻滚等微小运动。目标飞行过程中产生的多普勒可分解为匀速运动对应的固定平动多普勒和目标微动对应的微多普勒。

雷达目标的多普勒定义为

(1)

式中：Φt(t)为目标匀速运动对应的相位角，Φm(t)为微动对应的相位角。微动产生的微多普勒频率为

(2)

载机飞行过程中，由于具有机翼等稳定机构，角度变化比较稳定,而雷达诱饵体积较小且多是接近导弹形状的锥柱状，易发生旋转，角度变化剧烈。因此从微多普勒角度分析，飞机的微多普勒按照一定规律分布,而诱饵的随机性运动使其微多普勒分布极其丰富，包括转动、抖动，甚至翻滚等特征，这是区别载机和诱饵的直接有效特征。

当雷达发射信号频率为5 GHz、载机与雷达的接近速度为300 m/s时，载机平动多普勒频率为10 kHz。图1是载机平动产生的多普勒频率仿真图，可见由于噪声干扰，以频率为10 kHz的轴线上下起伏。噪声较小可以滤去，可知载机的多普勒频率恒为10 kHz,与时间和距离无关。事实上，载机也存在一定程度的微多普勒，但角度变化比较稳定，其微多普勒特性并不明显。

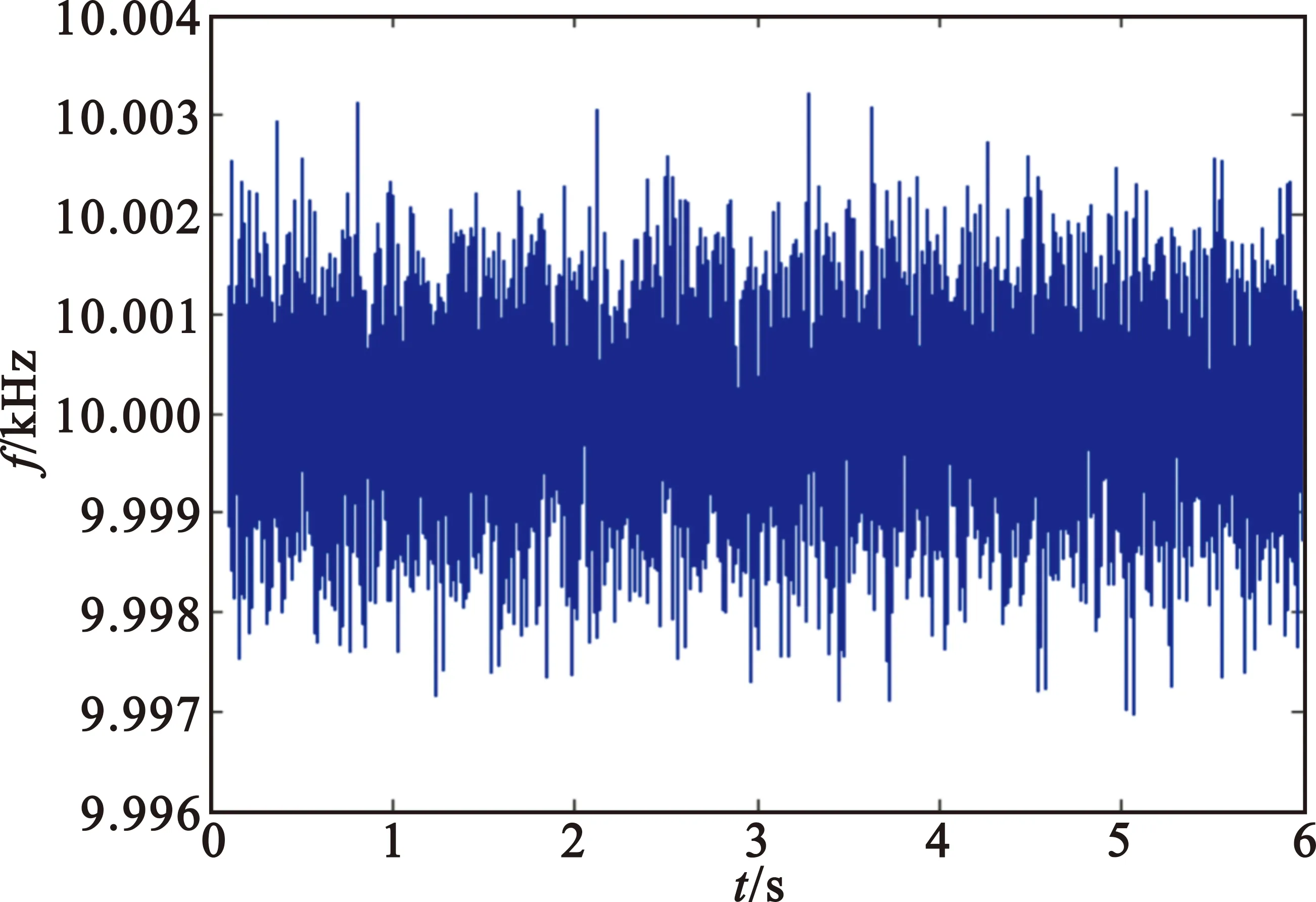
图1 载机多普勒频率Fig.1 Doppler frequency of carrier aircraft

雷达在探测诱饵时，不仅接收到平动多普勒频率，同时接收到微动多普勒频率。以转动为例，设点目标P绕O匀速转动，O位于点为雷达扫描平面内，转动模型见图2。

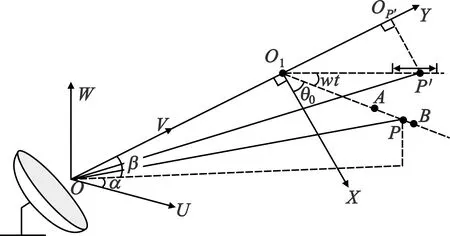
图2 转动模型示意图Fig.2 Schematic figure of rotation model

转动中心O与雷达的距离为R，转动角速度为ω，且同时沿雷达视线水平运动，运动速度为v。不考虑水平运动，在t=0时刻，目标上一散射点P在目标坐标系(X,Y)的坐标为(x0,y0)，t时刻转动到P′点，其在目标坐标系的坐标为(xt,yt)，且P′点在雷达视线上的投影为Op′。α和β为目标在雷达坐标系(U,V,W)中的俯仰角和方位角。

经推导计算，可近似得到转动时点目标的微多普勒频率为

(3)

假设诱饵上的一个散射点距旋转轴距离为0.5 m，诱饵旋转角速度为3.14 rad/s。代入式(3)，可得如图3所示的诱饵的微动多普勒频率仿真结果。由图可知，诱饵的微动多普勒频率以余弦形式振动，周期为2 s,振幅约为50 Hz。与图1所示的载机的多普勒频率相比较，区别显著。

图3 诱饵微动多普勒频率Fig.3 Micro-Doppler frequency of decoy

为了区分载机和诱饵，提取其频域波形熵特征[10]。频域波形熵用于描述频域能量的散布程度，即衡量谱线的间隔程度。熵值越小说明能量越集中，频域谱线越集中，谱线间隔越小。

设变量x=(x1,x2,…,xn)，x指雷达驻留时间内目标多普勒域回波数据，xi出现的概率为pi，则频域波形熵可以定义为

(4)

对载机而言，只考虑平动多普勒，其频域波形仅存在一条谱线，而对于诱饵，还存在微动多普勒，即其频域波形在平动多普勒谱线周围还存在一些边带分量。微动多普勒频率远远小于平动多普勒频率，使得诱饵回波多普勒频谱展宽，谐波分量增强，边带频率即为微多普勒频率。因此，对于载机和诱饵，载机的熵趋近于零，远小于诱饵，所以可提取回波信号的这一特征进行载机和诱饵的识别。

2.2 目标极化特征提取

载机与诱饵的回波信号中极化特征存在明显差别。目标在特定姿态和频率下的极化散射特性可用极化散射矩阵来完全表征[11]。

设目标单基地雷达的极化散射矩阵为S，极化基旋转后的散射矩阵为S′，

(5)

S′=RT(φ)SR(φ)，

(6)

Δ=det(S′)=det(RT(φ)SR(φ))=det(S)。

(7)

与极化散射矩阵对应的Graves功率矩阵及其迹可表示为

G=SHS，

(8)

Tr(G)=|S11|2+|S22|2+2|S12|2。

(9)

功率散射矩阵的迹实质上表征目标的全极化RCS值，可大致反映目标的大小，进而反映目标对入射电磁波的电磁散射能力。图4分别给出了雷达发射电磁波频率为5 GHz时载机和诱饵的功率散射矩阵的迹的分布情况。

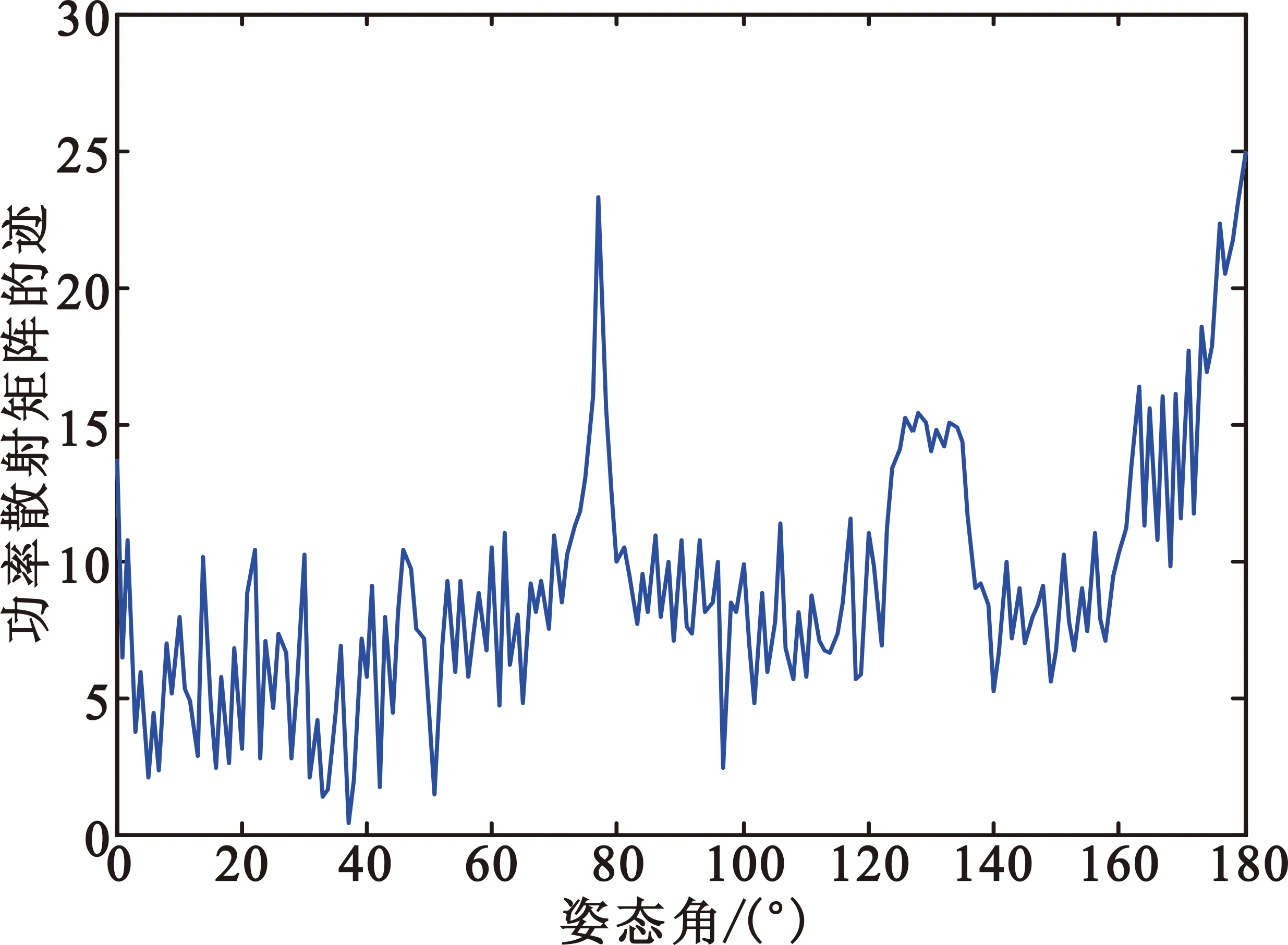
(a)载机

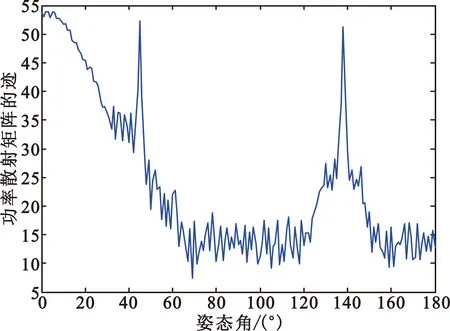
(b)诱饵图4 载机、诱饵的功率散射矩阵的迹Fig.4 The trace of carrier and decoy power scatter matrix

由图4中的对比可知，方位角较小或较大时，诱饵的功率散射矩阵的迹下降快，上升也快；载机的功率散射矩阵的迹波动较缓。综合比较，诱饵较载机波动大，且幅值也大，对方位角变化敏感。因此，载机与诱饵在电磁散射强度上有极大差异，而且随姿态角的变化趋势也明显不同，可以为两类目标的区分提供良好的特征量。

2.3 目标RCS特征提取

考虑到携带的方便性，诱饵的外形尺寸和载机差别很大。由于RCS与角度之间的变化关系，使得雷达回波强度具有不同的统计特征。这种统计特性可以作为目标识别的一种手段。

目标的RCS是随机变量，构成一个随机过程，可求取其统计特性，如均值、方差、各阶中心矩和概率密度分布等作为目标识别的特征。为了清晰地区分载机和诱饵，对原始的RCS时间序列进行数据处理。下面分别对载机和诱饵的RCS时间序列作N点截图,取N=20。将原始RCS时间序列划分为每20点的数据子集，计算子集均值和方差，表示RCS均值与可变性的整体特征。

由图5可知，载机、诱饵的均值和方差分布特性差异明显。其中，载机的RCS均值在分布在7 m2附近，方差集中在区间[6,10]，均值-方差分布紧密，集中在一块区域；诱饵的均值-方差分布零散，均值分布在区间[12，16](单位m2)，方差区间为[10,30],无论均值还是方差，波动范围均广。这是由于载机有姿态控制装置，在飞行中能保持平衡稳定，所以载机雷达截面积较稳定，方差小；但诱饵无此装置，飞行中受力不均，会出现各种微动，导致RCS起伏不均，方差波动大。

图5 RCS时间序列的均方差二维联合分布Fig.5 The two dimensional joint distribution of RCS time series mean square deviation

3 Bayes数据融合

Bayes方法在已知先验概率和条件概率的情况下，其识别错误率是最小的，它为载机和诱饵的特征融合识别提供了一条有效途径。

假设有一个N类问题ωj(j～1,2,…,N),每类的先验概率为P(ωj),对于一个D维的特征随机矢量X(x1,x2,…,xD)T,其每类的条件概率为P(X/ωj)。根据贝叶斯公式,可得后验概率

(10)

若X的各分量相互独立,将条件概率[12]代入式(10)得

(11)

Bayes最后的判决规则为

(12)

则X∈ωj。可以证明,Bayes判决规则的分类错误率是最小的。

3.1 一级融合

对于识别载机和诱饵来说是一个两类问题,即N=2。取载机和诱饵的训练样本数各100，对训练样本进行训练学习，然后取200个测试样本进行贝叶斯分类。载机和诱饵的仿真参数与上述一致，即雷达发射信号频率为5 GHz，载机拖着诱饵与雷达的接近速度为300 m/s,诱饵上的一个散射点距旋转轴距离为0.5 m，诱饵旋转角速度为3.14 rad/s。

载机与诱饵识别的基本步骤如图6所示。

图6 目标识别模型Fig.6 The model of target recognition

对训练样本进行训练，可得到3种特征各自的先验概率。由于N=2，取两类类条件概率相同，各为0.5。决策为载机的后验概率与决策为诱饵的后验概率和为1，经过Bayes公式计算，当后验概率大于0.5时判定为目标，小于0.5时判定为诱饵。

取其中10个测试样本(6个为目标，4个为诱饵)，根据式(10)，决策为载机的后验概率如图7所示。分别直接利用3种单一特征对载机和诱饵进行分类，由图可知，分别判定为两类的后验概率值相差不大，容易出现判断错误。如：对于测试样本7，利用微多普勒单独决策时，后验概率小于0.5，而利用另外两种特征决策时概率大于0.5，即出现识别错误。

为了提高识别率,进行贝叶斯融合。首先分别对上述3种特征进行一级融合。根据公式(11)，可得到该10个测试样本一级融合后的载机后验概率如图7所示。由图，融合后，载机的后验概率存在显著提高。测试样本2、6、8、10决策判为诱饵，其余6个决策为目标。此时，对于测试样本7，后验概率明显大于0.5，进而判定为载机。因此，通过一级融合，载机和诱饵的识别正确率可得到提高。

图7 融合前后后验概率Fig.7 The posterior probability before and after fusion

3.2 二极融合

二级融合是在一级融合的基础上，对不同时刻的数据进行再融合。不同时刻二级融合后目标后验概率如图8所示。由图可知，t=0，即二极融合前载机后验概率约为0.85，随着融合时间的延长，决策为载机的后验概率随之增大，并且，当时间足够长时，后验概率可达到100%。这是因为融合后随融合时间t增长，识别特征维数随之增加，诱饵识别率自然会增大，但是信号特征需要一一比较，识别工作量也会呈几何增长，这就易造成识别不实时。因此，在实际过程中，需要考虑平衡。

对200个测试样本进行分类识别，得到融合前后识别结果，如表1所示。

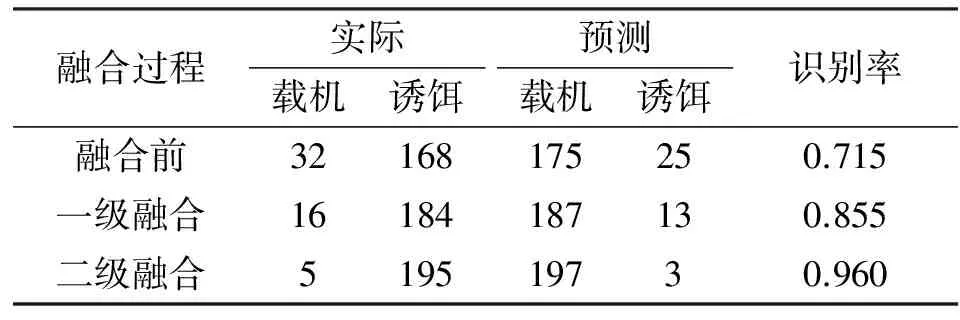
表1 载机诱饵识别结果Tab.1 The identification results of carrier aircraft and decoy

由表1知，通过雷达回波信号的特征可对目标和诱饵进行识别。在进行数据融合前载机诱饵的识别率为71.5%，经过一级融合识别率提高到85.5%，两级融合后，该识别率提高到96%。可见，Bayes数据融合使得载机和诱饵的识别率有了显著提高，说明贝叶斯融合是一种行之有效的数据融合方法。

4 结束语

雷达诱饵和载机的识别，特征提取和利用是关键，但是利用单一特征进行识别，识别率不高。本文提出了一种对雷达回波信号微动多普勒特征、极化特征和雷达截面积序列统计特征3种典型特征进行Bayes数据融合来识别拖曳式诱饵和载机的方法，可使载机和诱饵识别率达到96%，相对于极化单特征识别，目标识别率大大提高。随着电子对抗技术的发展，新型诱饵可以产生各种调制的模拟回波信号模仿各型载机的雷达回波特征。对于这种新型诱饵特征本融合方法需改进利用，可以考虑结合多传感器融合技术实现载机与诱饵的有效识别。基于信息融合的目标识别技术必将成为雷达目标识别问题研究的一种有效途径。

[1] 姬晓琳．拖曳式诱饵干扰机理研究[M]．西安:西安电子科技大学，2010.

[2] 周栋. 拖曳式诱饵对抗方法探讨[J].制导与引信,2010，31(2)：12-16. ZHOU Dong. Countermeasure discussion of towed decoy[J].Guidance and Fuze,2010,31(2):12-16.(in Chinese)

[3] ZHAO J. Flight test method discussed for airborne towed radar active decoy[J].Aeronautical Science and Technology,2015(2):42-46.

[4] DONGLI M A,LIU Y,LIN P. Study of dynamic characteristics of aeronautic towed decoy system[J].Acta Aeronautica Et Astronautica Sinica,2014,35(1):161-170.

[5] MENG Y,BIN L I,CHENG S,et al. Detection of mono-pulse radar seeker for towed decoy[J].Journal of Projectiles Rockets Missiles and Guidance,2014(4):17-20.

[6] 孙希东,李晓江,梁智勇. 拖曳式诱饵及其对抗技术发展综述[J].航天电子对抗,2015,31(5):54-59. SUN Xidong,LI Xiaojiang,LIANG Zhiyong. Survey on the development of towed decoy and its countermeasure technology[J].Aerospace Electronic Warfare,2015,31(5):54-59.(in Chinese)

[7] 马国哲,赵毅寰,刘哲. 一种基于Radon-Wigner变换的拖曳式诱饵辨识方法[J].现代防御技术,2016,44(1):161-165. MA Guozhe,ZHAO Yihuan,LIU Zhe. A method of distinguishing towed radar active decoy based on Radon-Wigner[J].Modern Defence Technology,2016,44(1):161-165.(in Chinese)

[8] 张强. 有源诱饵的双极化识别[J].电讯技术,2015,55(2):168-174. ZHANG Qiang. Dual polarization identification of active decoys[J].Telecommunication Engineering,2015,55(2):168-174.(in Chinese)

[9] JASTRAM N,FILIPOVIC D S. Design of dual-polarized millimeter wave constant EIRP front-end for towed decoy platforms[C]//Proceedings of 2014 International Conference on Electromagnetics in Advanced Applications. Denver,CO:IEEE,2014:1-5.

[10] KULKE R,LAM H Y,HGELEN M,et al. Classification of moving targets using mirco-Doppler radar[C]//Proceedings of 2016 International Radar Symposium(IRS). Krakow,Poland:IEEE,2016:1-6.

[11] 李永祯,王雪松,王涛,等. 有源诱饵的极化鉴别研究[J].国防科技大学学报,2004(3):83-88.

LI Yongzhen,WANG Xuesong,WANG Tao,et al. Polarization discrimization algorithm of active decoy and radar target[J].Journal of National University of Defense Technology,2004(3):83-88.(in Chinese)

[12] 王慧频,徐晖,孙仲康. 采用Bayes数据融合方法进行目标和诱饵的识别[J].国防科技大学学报,1996(2):59-64. WANG Huipin,XU Hui,SUN Zhongkang. Identification of targer and decoy by Bayes data fusion[J].Journal of National University of Defense Technology,1996(2):59-64.(in Chinese)

Target Recognition Technology of Towed Radar Decoy

XIAO Jing,WANG Hong,LI Yuehua,ZHANG Guangfeng
(School of Electronic Engineering and Optoelectronic Technology,Nanjing University of Science and Technology，Nanjing 210094,China)

For the problem that the deception jamming to radar seeker is easily caused by towed radar decoy(TRD),the target micro-Doppler,the polarization and radar cross section(RCS) sequence features extracted from radar echo signal are employed to perform simulation and analysis. On the basis of primary recognition of carrier aircraft and decoy,Bayes data fusion method is used to perform the first-stage integration of three echo signal features and the second-stage integration of signal features at different time. Finally,the target recognition rate is increased from 71.5% to 96%.The proposed method reduces the influence of external factors and significantly increases the recognition rate compared with the single feature recognition method.

towed radar decoy(TRD);target recognition;radar seeker;deception jamming;Bayes data fusion

2016-06-14；

2016-09-07 Received date:2016-06-14；Revised date：2016-09-07

国家自然科学基金面上项目(61371038)

10.3969/j.issn.1001-893x.2017.02.010

肖晶，王虹，李跃华，等.拖曳式雷达诱饵目标识别技术[J].电讯技术，2017,57(2):180-185.[XIAO Jing,WANG Hong,LI Yuehua,et al.Target recognition technology of towed radar decoy[J].Telecommunication Engineering,2017,57(2):180-185.]

TN97

A

1001-893X(2017)02-0180-06

肖 晶(1992—)，女，安徽宣城人，硕士研究生，主要研究方向为信号与信息处理；

Email:1445625928@qq.com

王 虹(1976—)，女，吉林通化人，2014年获博士学位，现为助理研究员，主要研究方向为毫米波辐射计系统设计及其信号处理；

Email:whnjust@163.com

李跃华(1959—)，男，江苏宿迁人，博士，教授,主要研究方向为毫米波亚毫米波近程探测系统设计、目标识别、信号处理与智能化技术；

张光锋(1975—)，男，河北石家庄人，博士后，副教授,主要研究方向为毫米波被动成像技术。

*通信作者：1445625928@qq.com Corresponding author：1445625928@qq.com