军事空运路径与装载联合优化问题研究

颜 瑞，马晓娟，梁廷政，王 雷

(1.北京信息科技大学，北京 100192； 2.北京科技大学，北京 100083；3.北京市可持续发展科技促进中心，北京 100035； 4.中国刑事警察学院，沈阳 110035)

军事空运路径与装载联合优化问题研究

颜 瑞1，马晓娟2，梁廷政3，王 雷4

(1.北京信息科技大学，北京 100192； 2.北京科技大学，北京 100083；3.北京市可持续发展科技促进中心，北京 100035； 4.中国刑事警察学院，沈阳 110035)

为了有效、快速制定军事空运路径和装载方案，在计算出最优运输路径的同时获取可行装载方案，针对军事空运路径和装载的联合优化问题进行研究。建立军事空运路径和装载联合优化模型，提出一种结合量子粒子群算法和引导式局部搜索算法的混合算法进行求解，通过数值试验检验模型的可行性和算法的有效性。试验结果表明，联合优化模型能够有效实现军事空运路径和装载联合优化问题的建模过程，且混合算法能够有效获取联合优化模型的近似最优解。

军事空运；路径方案；装载方案；联合优化；量子粒子群算法

0 引 言

第二次世界大战后，航空军事运输发展十分迅速，空运的作用越来越大。军事空运在军事作战和训练、支援国家建设、抢险救灾中，都发挥着重要作用。组织军事空运，须根据接收地域的场地条件和部队需要，采取着陆空运(机降)或非着陆空运(空投)的方法，并注意物资的包装、捆绑和装载，以提高运输效能[1]。装载方案和路径方案是军事空运的两个重要决策内容。实现军事空运装载方案和路径方案的快速、优化生成，保证装备物资安全、可靠、快速到达目的地，是战时空运保障和应急救援保障的首要任务。

目前，针对军事空运装载方案和路径方案优化的研究是独立进行的，且分别产生了许多研究成果[2-5]。但是，独立优化装载方案和路径方案往往会产生一些不合理方案。比如，在优化路径方案通常需要考虑物资重量和体积，但由于物资打包规格不一致、机舱承载装载空间不规则等原因，容易造成物资无法全部装入机舱内或者浪费大量装载空间的情况。为了避免产生不合理方案、提高军事空运效率，有必要将装载方案和路径方案联合起来进行优化，建立联合优化模型并设计求解算法。

1 模型建立

1.1 问题描述及模型假设

军事空运装载方案与路径方案联合优化问题的建模和求解可以参考带装箱约束的车辆路径问题，但需要考虑更多的装载要求和运输要求。军事空运装载方案与路径方案联合优化问题可以描述为：集中仓库储存着足够量的各类军事物资，机场有一定数量的运输机可供调度，在一定区域内分布着多个物资需求点，每个需求点需求不同数量、不同类型的物资，仓库与需求点之间、每两个需求点之间均有固定航线，决策目标是得到一个使用运输机数量最少、消耗总时间最短的运输机调度和飞行路径方案，并且同时获取每架飞机的可行装载方案。

军事空运装载方案与路径方案联合优化模型的假设：

(1)假设物资仓库与机场各有一个且位置相同，即不考虑物资从仓库搬运至运输机的过程；

(2)任意两个节点之间均有固定航线，运输机可以执行所有航线上的任务，所有运输机为同一型号；

(3)确定不超过运输机数量的回路作为运输机飞行路线，每条回路总长度不超过运输机最大航程，所有回路均从机场出发并返回机场；

(4)每个需求点只能在一条回路上，每条回路上的需求点仅由一架运输机服务(即为非满载运输问题)；

(5)不考虑起飞和降落过程，在同一条航线、同方向上，所有运输机均以相同速度匀速飞行，在不同航线或相对方向上，运输机的速度可能不同；

(6)每条回路上需求点的物资需求总重量不能超过运输机的最大载重，物资总体积不能超过运输机机舱内的最大容积；

(7)每件物资均打包成长方体形状，机舱内空间可被分割成若干个装载区域，每个区域均为长方体；

(8)所有物资均从运输机尾部的舱门进出，装货过程从运输机内侧左下角开始，假设装货工具可以把物资摆放到运输机内的任意位置；

(9)每条回路上物资需求点的物资必须全部装入运输机内，且满足全部给定的装载约束；

(10)以所有运输机的飞行时间之和最小为目标。

军事空运装载不仅要求承载量最大、空间利用率最高，更要满足作战要求，实现军事价值最大化。因此，除了以上假设中的(6)、(7)和(8)之外，还需要考虑如下装载约束：

(1)基本装载约束：物资不能悬空放置、不能重合放置，单件物资的体积不能大于机舱可装载空间；

(2)方向性约束：物资边缘必须与相应的车厢边缘平行，所有物资均区分顶部和底部，且物资必须顶部朝上放置，物资只能在水平面上做90°的旋转，不能以其它角度或者在垂直面上旋转；

(3)稳定性约束：上下堆叠的物资之间不能有空隙，且上下层两个物资的直接接触面积不能小于上层物资底面积的ρ(ρ为给定常量，0.5≤ρ≤1)倍，下层如有多个顶部平齐的物资可被视为一个物资；

(4)LIFO(Last-in-First-out)约束：军事空运对时间要求非常高，决不允许在装卸货过程中执行不必要的操作，此外还须应对突发状况导致无法着陆时空投物资的情况，因此，必须满足“先进物资后出，先出物资后进”的约束，以满足连续执行装卸货作业的要求；

(5)平衡性约束：如果载货之后的运输机重心偏移过大，则会大幅增加操控难度、降低任务执行效率，因此，必须保证运输机前后、左右的载货重量之差在规定范围内；

(6)安全性约束：对于防压、防震、防潮、防冻的仪器设备类以及危险类物资，除了在装载前需要进行适当的包装处理之外，装载的时候还应确保其放置在安全位置，可假设该类物资的长宽为实际长宽加上安全间隔宽度，且假设物资的高度与机舱高度一致(即其上方不可放置其他物资)，为了简化模型，本文将所有物资归为如下两种类型：普通物资，可堆叠摆放；防压物资，其上方不可堆叠放置其他类型物资，可放置同类物资。

1.2 模型符号及符号解释

建立联合优化模型之前需要将机舱空间转化为，以机舱内侧左下角为坐标原点，以机舱最边缘的长、宽和高为坐标轴，建立笛卡尔坐标系。表1给出模型中的所有符号，并解释每个符号的意义。

表1 模型符号及符号解释

1.3 数学模型

(1)

(2)

(3)

(4)

(5)

(6)

(7)

(8)

(9)

目标函数(1)表示最小化所有运输机的飞行总时长；式(2)表示所有物资需求节点仅被访问一次；式(3)和式(4)表示运输机从物资仓库出发，执行完任务之后返回物资仓库；式(5)表示运输机进入某节点，也必须从该节点离开；式(6)表示每架运输机装载货物的重量之和不超过运输机限制载重；式(7)表示每架运输机装载货物的体积之和不超过运输机限制容积；式(8)绑定了装载优化变量和路径优化变量；式(9)为支路消除约束，保证任何路线中只包含一个物资仓库。

在建立装载优化模型之前，需要先建立一个笛卡尔坐标系。坐标系的坐标轴分别对应于运输机外切长方体的长、宽和高，如图1所示。

图1 运输机外切长方体及笛卡尔坐标系示意图

在图1中，用间距相等的网格线将运输机外切长方体分割成若干个小立方体，当网格线足够密集时可以保证所有物资占用立方体的个数为整数(当网格线间距小于等于物资尺寸示数的最小单位时即可)。运输机的不同装载区域均处于外切长方体之内，当某装载区域的边缘未达到长方体边缘时，可将装载区域与外切长方体之间的立方体全部标记为已被占用。

货物i底部左前方的位置用坐标A(x,y,z)表示，则有：x∈X={0,1,…,L-minik(lmik)}，y∈Y={0,1,…,W-minik(wmik)}，z∈Z={0,1,…,H-minik(hmik)}，其中k=1,2,…,K，i=1,2,…,Np。

受到物资三维形状的限制，即使单架运输机的物资总体积小于其装载空间总容积，也有可能发生无法将所有物资全部装入机舱内的情况。考虑到这一点，本文以最大化装入机舱内的货物总数为目标建立装载优化模型，则可行解的目标函数值等于物资总数。装载优化模型如下：

(10)

(11)

(12)

(13)

(14)

(15)

(16)

(17)

其中，(x′,y′,z)表示另一个物资底部左前方的可能位置坐标，σi表示货物顶部任意一点所能承受的最大压强。注意，在路径优化模型中i表示顾客，而在装载优化模型中i表示物资。式(10)为目标函数，最大化装入运输机的总货物数；式(11)保证了所有物资都必须有支撑区域(不可悬空放置)；式(12)用以区分不同物资类型的摆放要求；式(13)和(14)分别表示运输机在x轴和y轴上的重心约束；式(15)给出了决策变量；式(16)和式(17)计算货物i的长和宽。模型中的变量和标识详见文献[6]和文献[7]。

2 算法设计

本文提出一种结合量子粒子群算法和引导式局部搜索算法的混合算法求解军事空运装载与路径联合优化模型。本节将详细描述混合算法的基本原理、各部分策略和实施步骤。

2.1 改进的量子粒子群算法

2.1.1 基础量子粒子群算法

美国学者Kennedy和Eberhart受到鸟群觅食行为的启发提出了粒子群算法(Particle Swarm Optimization，PSO)，PSO具有精度高、收敛快和容易实现等优点[8]。算法提出后不久就被用于求解VRP问题，目前已有许多运用PSO求解VRP及其变种问题的文献[9, 10]。在标准PSO中，种群由一定数量的粒子组成，每个粒子的位置均代表一个可行解。在多维搜索空间中，每个粒子均按照某个特定速度向更好的解移动。

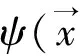
mbest(t)=(mbest1(t),mbest2(t),…mbestd(t))=

(18)

(19)

u=rand(0,1)

(20)

其中，M表示粒子群中粒子的数目；d为粒子维度；mbest表示在所有粒子中每个粒子搜索到的最优位置的平均值，本文采用最接近平均适应值的粒子所在的位置；Pi=(Pi1,Pi2,…,Pid)表示第i个粒子的最优位置；Pgd表示所有粒子中最佳粒子所在的位置；pid表示在Pid和Pgd之间的一个随机点，在第i个粒子d维空间的一个位置；φ和u是在[0,1]之间均匀分布的随机数；α是QPSO算法的参数，称为收缩-扩张系数，一般采用线性递减的方式取值，其公式为：

(21)

量子粒子群优化算法过程如下：

Step1.初始化种群，粒子的初始位置通过随机方式产生；

Step2.对于每一个粒子，计算其适应值，保存每个粒子历史最优值Pid，以及所有粒子的最优值Pgd；

Step3.根据公式(18)计算mbest，即最接近所有粒子的平均适应值的粒子所在位置；

Step4.对于粒子的每一个维，通过公式(19)得到一个随机点；

Step5.通过公式(20)获得一个新的位置Xid；

Step6.执行局部扰动操作；

Step7.重复Step2-Step6，直至达到最大迭代次数。

2.1.2 局部扰动

为了提高QPSO的寻优效率，本文采用2-opt和线路内部搜索两个方法进行局部扰动，这两种方法类似于遗传算法中的变异算子。2-opt作用于两条线路上，具体操作方法是：随机选择两条线路，并随机选择两个位置，将两条线路上的对应节点进行互换。线路内部搜索作用于单条线路上，具体操作方法是：随机选择一条线路，并随机选择两个位置，将两个位置对应的节点进行互换。

2.2 引导式局部搜索算法

由2.1中的量子粒子群算法可求解得最优路线，并可以确定每条路线上有哪些物资需求点。本节讨论如何将物资装入各自机舱内，且满足所有装载约束。一般的装箱问题以装载货物数最大为目标，而在军事空运装载与路径联合优化模型的装载问题中每架运输机装载的货物数量和形状是固定的，因此其解空间仅是一般装箱问题解空间的一个子集。针对这样的特点，我们将设计一系列引导策略搜索问题的局部最优解。联合优化模型的装箱过程包括确定待装货物顺序和确定可行装货位置两个子问题，下面分别给出这两个子问题的求解策略。

2.2.1 确定待装货物顺序

对于一条给定的运输路线而言，该线路上的所有物资需求点及其顺序是固定的。在当前需求点执行卸货任务时不可以用挪动其他需求点的货物，因此同一条线路上的物资应首先按照执行任务的顺序逆向安排，遵循后进先出原则。因此，不同物资需求点的物资装箱顺序是固定的，但是同一个需求点的货物装箱顺序并不唯一。本文采用Oj(j=1,2,3)规则中的一个规则对初始货物顺序进行调整，确定最终货物装载顺序[6]。对于初始装货序列中相同级别的货物(属于相同顾客且同为非易碎品或同为易碎品的货物)，O1、O2和O3分别表示把货物按体积(w·l·h)、底面积(w·l)和高度h的降序进行排列，其意义在于：O1规则优先装载体积较大的货物，以占据较大的可行装货空间；O2规则优先装载底面积较大的货物，为后续装载的货物提供较大的支撑区域；O3规则优先装载较高的货物，因为较小的货物更容易放在其他货物之上。

2.2.2 确定可行装货位置

机舱内的可行装货位置指的是装货列表中的下一个货物能够放置的位置。每装入一个货物之后，可行装货位置会发生变化。通常可行装货位置并不唯一，那么我们需要对可行装货位置按某种规则进行排序。已发表的文献中给出了几种确定可行装货位置的方法，但是这些方法通常仅按照固定的规则逐一尝试，容易造成后面的货物不能全部装入车厢，需要进行重复计算，降低了求解效率。因此，本文给出一种新的基于匹配规则的启发式装箱方法，充分考虑到货物与位置之间的匹配关系，将待装货物放在最合适的位置上，尽可能充分节省空间，以提高一次装箱成功率。

对于列表中的第一个货物，我们通常将它放置在机舱内的左下角。当我们描述把货物放在某个位置时，则表示该货物左下角的坐标落在该位置点上。此外，由于所有货物占据的网格数均为整数，因此某个点被货物占据的意思就是，包含该点且处于其右上方的网格被该货物占据。例如，点O处放置一个货物，则(0, 0)、(0, 1)、(1, 0)和(1, 1)所组成的网格被该货物占据。当装入一些货物之后可能会出现一系列新的装货位置。

在所有的可行装货位置中，我们下一步要做的事情就是根据当前货物的形状，选择一个最理想的位置作为当前装货位置。在确定最理想装货位置的时候，我们应当遵循一个最基本的原则，就是充分节省空间。基于这样的原则，我们给出如下规则对可行装货点进行排序，得到每个可行装货点的优先级。本文采用引导式排序方法给出可行装货位置顺序，引导式排序方法包括“Back-Left-Low”、“Left-Back-Low”、“Max-Touching-Area-Y”、“Max-Touching-Area-No-Walls-Y”、“Max-Touching-Area-X”及“Max-Touching-No-Walls-X”等六种[11]，实际操作中依次选择六种方法中的一个，直至找到可行装载方案。具体实施方法见文献[11]。

2.3 混合算法

本文把量子粒子群算法和引导式局部搜索算法结合起来，构造求解军事空运装载与路径联合优化模型的引导式局部搜索量子粒子群算法(Guided Local Search-Quantum-behaved Particle Swarm Optimization Algorithm，GLS-QPSO)。GLS-QPSO算法的基本思路为：通过量子粒子群算法得到路径优化模型的近似最优解集，近似最优解集中保存适应度靠前的若干粒子；把最优解集中的粒子按适应度从大到小排列，选择第一个粒子作为当前运输路线方案，然后调用引导式局部搜索算法；如果找到可行装箱方案，则返回最优解，否则，依次选择最优解集中的下一个解作为运输路线方案；如果最优解集中所有运输路线方案均找不到可行解，则返回量子粒子群算法重新求解路径优化问题；重复算法直至找到可行解，或达到最大迭代次数。若达到最大迭代次数仍未找到最优解，则应考虑减少需求点或物资数量，或者增加运输机总数，然后重新执行GLS-QPSO算法。

3 数值试验

假设某次战斗需要应急空运一批装备物资，已知条件有：1个物资仓库(机场)，8个物资需求点(P1，P2，…，P8)，坐标如图2所示，在图2中每单位距离表示150 km；3架某型号运输机可供调度，参考文献[]中的飞机参数设定，飞机允许重心范围为20%bA～40%bA(bA为平均空气动力弦)，具体数值见表2；共有6种物资需要运送，物资规格见表3；物资仓库备有充足物资，各个需求点的物资需求量见表4。

数值试验采用Matlab 7.1软件实现，计算机CPU为英特尔酷睿Ⅱ、2.67GHz，4GB内存，64位windows 8操作系统。

图2 机场及物资需求点坐标示意图

型号货舱长度货舱宽度货舱高度巡航速度最大有效载重最大油量航程运-818 0m3 0m3 0m550km/h20t3440km

表3 物资规格参数

表4 各需求点的物资需求量

通过优化得到3条运输机航行线路，且飞机的可行装载方案均全部找到。所有飞机行驶总距离为601.9 km，具体线路为：

Route1：Depot-N2-N3-Depot，物资总重量10 753 kg，飞机行驶距离219.5 km；

Route2：Depot-N1-N4-N5-Depot，物资总重量13 808 kg，飞机行驶距离211.8 km；

Route3：Depot-N6-N7-N8-Depot，物资总重量18 084 kg，飞机行驶距离170.6 km。

4 结 语

在现有关于军事空运的研究成果中，通常分别研究空运线路优化和空运装载优化这两个问题，实际应用中具有很大的局限性。本文将路径方案和装载方案联合起来进行优化，能够有效避免产生不可行方案、提高军事空运效率。数值试验表明，本文所提出的模型和算法具有很好的应用效果，能够有效解决军事空运路径和装载联合优化问题并进行求解。本文模型具有较强的扩展性，实际应用中可根据具体情境设置、调节模型参数，或者适当增加、删减部分约束条件。比如，考虑起飞和降落过程中的非匀速飞行状态，可将飞行速度设定为分段函数；考虑到油量与航程之间的关系，可将油量作为载重货物一并计算重量，同时飞机的最大航程则要转换为油量的非线性函数；物资需求点对物资供应时间有较高要求，可增加时间窗约束；等等。

[1] 周树德. 基于分布估计算法的军事物流配送中心选址决策[J]. 中国电子科学研究院学报, 2010, 05(5): 532-536.

[2] 孟冲，宋华文，陈柏松. 基于0-1整数线性规划的军事空运装载优化算法[J]. 西南交通大学学报，2011，46(3): 500-505.

[3] 张军，陈柏松，王新虎，李良峰. 军事空运装载问题的禁忌搜索算法实现[J]. 国防交通工程与技术，2010，8(6)：10-13.

[4] 孟冲. 航空兵应急转场空运装载方案优化研究[D]. 西安：空军工程大学，2009.

[5] Marcel Mongeau, Christian Bes. Optimization of aircraft container loading[J]. IEEE Transactions on Aerospace & Electronic Systems, 2003, 39(1): 140-150.

[6] Ruan QF, Zhang ZQ, Miao LX, et al. A hybrid approach for the vehicle routing problem with three-dimensional loading constraints[J]. Computers & Operations Research, 2011, 38(11): 1-11.

[7] Junqueira L, Morabito R, Yamashita DS. Three-dimensional container loading modes with cargo stability and load bearing constraints[J]. Computers & Operations Research, 2012, 39(1): 74-85.

[8] Kennedy J, Eberhart RC. Swarm Intelligence[M]. Morgan Kaufman Publishers, San Francisco, 2001: 3-54.

[9] Ai T, Kachitvichyanukul V. A particle swarm optimization for the vehicle routing problem with simultaneous pickup and delivery[J]. Computers & Operations Research, 2009, 36(5): 1693-1702.

[10]Wu Z. Optimization of distribution route selection based on particle swarm algorithm[J]. International Journal of Simulation Modelling, 2014, 13 (2): 230-242.

[11]Tarantilis CD, Zachariadis EE, Kiranoudis CT. A Hybrid Metaheuristic Algorithm for the Integrated Vehicle Routing and Three-Dimensional Container-Loading Problem

[C]. Transactions on Intelligent Transportation Systems, 10(2): 255-271.

颜 瑞(1986—)，江苏人，讲师，博士，主要研究方向为物流优化、智能算法；

马晓娟(1994—)，宁夏人，硕士研究生，主要研究方向为项目管理；

梁廷政(1981—),山西人，助理研究员，主要研究方向为项目管理；

王 雷(1980—)，辽宁人，讲师，博士，主要研究方向为应急管理、公共安全管理。

Research on Optimal Joint Problem of Routing and Loading in Military Airlift

YAN Rui1,MA Xiao-Juan2,LIAN Ting-zheng3,WANG Lei4

(1. Beijing Information Science & technology University, Beijing 100192; 2. University of Science and Technology Beijing, Beijing 100083; 3. The sustainable development of science and technology promotion center of Beijing, Beijing 100035; 4. National Police University of China, Shenyang 110035)

In order to formulate routing plan and loading plan in military airlift effectively and rapidly, as well as obtain the feasible loading plan while identifying the optimal transportation path, it is necessary to combine the routing problem and loading problem in military airlift together. This paper is an attempt to study the joint optimal model of routing and loading in military airlift. A hybrid algorithm of quantum behaved particle swarm optimization algorithm and guided local search algorithm is employed to solve this optimal joint model. The feasibility of this model and the effectiveness of the hybrid algorithm are tested by an experiment. The results of the experiment show that the optimal joint problem of routing and loading in military airlift can reflects facts more reasonably, and the hybrid algorithm can obtain the approximate optimal solution for this model.

military airlift; routing plan; loading plan; joint optimization; quantum behaved particle swarm optimization algorithm

10.3969/j.issn.1673-5692.2017.01.002

2016-10-15

2016-12-15

国家自然科学基金项目(71602008);北京市哲学社科规划项目(16JDGLC032);北京市哲学社科规划项目(14JDJC018);公安部公安理论与软科学计划项目(2016LLYJXJXY032);辽宁省社会科学规划基金项目(L16BGL042)。

U8

A

1673-5692(2017)01-007-07