风机叶片多点激振疲劳加载试验分析

乌建中，马 怡

（同济大学机械与能源工程学院，上海201804）

风机叶片疲劳加载试验的目的是测试叶片的可靠性和抗疲劳强度，确保叶片疲劳寿命达到设计要求。随着风机技术的发展，大批兆瓦级大型风机投入规模化的生产，单点加载可能难以驱动大尺寸叶片试验，而使用多套设备在不同点同时进行加载，即多点疲劳加载，可以加大激振能力，同时能更好地满足弯矩分布要求，提高测试频率，缩短试验时间[1-2]。本文建立了多点叶片疲劳加载振动模型，并以两点为例设计了多点疲劳加载系统。

1 风机叶片两点疲劳加载试验系统组成

风机叶片疲劳加载试验系统由加载基座、测试叶片、疲劳加载系统等构成，其中疲劳加载系统由动力装置、可移动质量块和固定部分等构成。风机叶片的根部固定在加载基座上，多点激振试验是多个加载源布置在沿叶片展向位置上，其动力装置驱动可移动质量块做直线往复运动，其产生的惯性力对叶片进行加载，以两点激振疲劳加载试验系统为例，如图1所示。

2 风机叶片疲劳加载振动模型建立

2.1 叶片模型离散化

将连续的叶片分为各截面，离散成一个具有自由度的等效悬臂杆体系，每个离散段为一个单元，由无质量的梁段及截面处的集中质量块组成，如图2所示。

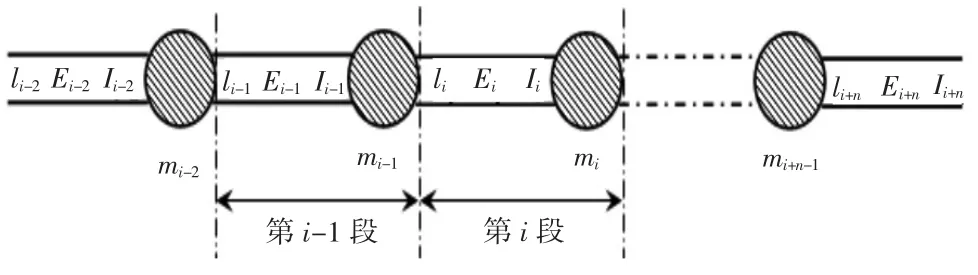
图2 叶片离散化模型

叶片根部记为截面1，尖部为截面n，截面i与截面i+1组成离散段i.离散段长度为li，截面线密度为ρi，则离散段i的质量近似为：

n自由度系统的运动微分方程为：

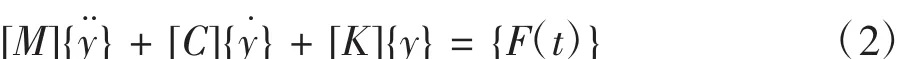
上式中：[M]为结构的质量矩阵，是对角线元素为集中质量mi的对角线矩阵；[K]为结构的抗弯刚度矩阵；[C]为结构的阻尼矩阵；{y}、{y˙}、{y¨}分别为结构的位移、速度和加速度；{F（t）}为激振力向量。

2.2 叶片系统受迫振动分析

多自由度系统的固有振动分析可归结为求解矩阵特征值问题，当自由度数较大时计算量非常大，本文采用传递矩阵法进行振动分析。离散化的等效悬臂杆体系中一个典型单元包括一个无质量梁段和一个集中质量 mi，分别如图 3（a）和（b）所示，用 4 个矢量来表示每个单元截面的状态量Z：挠度yi、转角θi、剪力Qi和弯矩Mi.

图3 梁段受和有激振力的集中质量受力图

传递关系式按顺序相乘，可得一个4×4矩阵，用u11与u44表示矩阵元素，得振动系统的状态矢量传递关系为：

由图3（a）及材料力学可得第i梁段的左端与第i-1梁段右端状态变量的传递关系：

因疲劳加载试验采取共振的方式，求解叶片振动系统的固有频率时不考虑激振力。由图3（b）忽略激振力Ff，非激振点的第i质量左右两侧状态变量的传递关系为：=0，代入式（8）得到：采用普劳尔法或借助计算机可求解出式（9）中的固有圆频率ω，进而得到该固有频率的主振型。

由齐次方程组有非零解的条件得：

假设激振力加载位置为集中质量的质心处，由图3（b）可得特定激振点f左右两侧剪力Qi的传递关系：

则激振点f左右两侧状态变量的传递关系为：

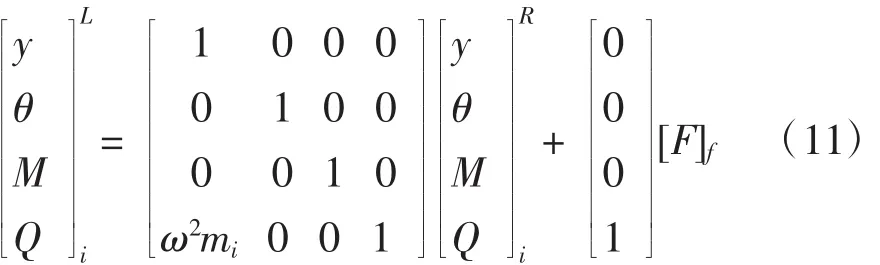
已知圆频率ω、集中质量mi、截面刚度EiIi和各分段长度 li，由式（4）、（5）和（11），可得受迫振动系统的各分段的挠度yi、转角θi、剪力Qi和弯矩Mi状态量。

2.3 叶片振动系统激振力分析

根据IEC61400-23规范[3]，疲劳加载试验时叶片展向上的弯矩分布要尽可能接近设计载荷弯矩，一般情况下，优先保证弯矩分布接近目标弯矩。为此通常在叶片不同位置上添加质量块，与叶片共同组成振动系统。

根据工程试验的需要，弯矩误差δ按实际情况取值。假设特定截面j添加的质量块质量为mj，则第j截面的集中质量总和为mi+mj.通常，直线驱动装置控制质量块相对于叶片做往复简谐振动，产生余弦规律变化的激振力对叶片进行加载，假设激振力Ff（t）=Ffcos（ωt+ φ），即激振力的幅值 Ff＝ mjSω2，mj为激振点运动质量块质量，S为运动质量块行程。对于单点惯性式加载，以叶片为参考系，质量块的位移为ym（t）=S cos（ωt）；叶片的位移为 y（t）=Yisin（ωt），Yi为激振点的挠度；则以地面为参考系，质量块的位移为ym（t）+y（t） =S cos（ωt） +Yisin（ωt）.

可求得激振力一个周期能量输入为：

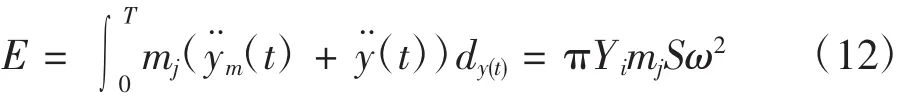
由 Ff=mjSω2可得：

当叶片在激振力的作用下运动时，在一个振动周期内所有离散段质量的动能为：

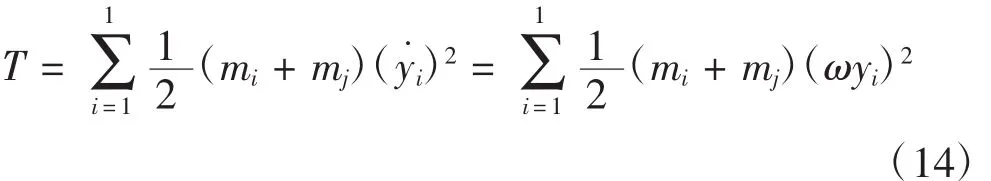
由此可以推导得到：

由式（13）和式（15）可求得激振力：

上式表达了单点激振力和动能的关系[4]，叶片在多点激振力作用下同样要满足动能关系式，则式（17）推及至多点激振，有如下表达式：

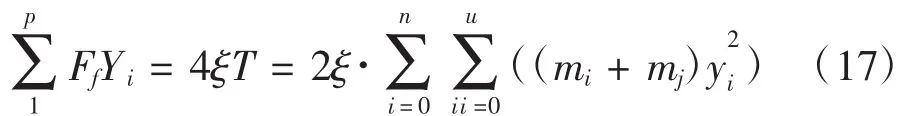
上式中：p表示激振点的个数，例如两点加载时p=2；Yi为激振点的挠度；yi为各分段截面挠度。

已知试验叶片n分段的集中质量mi、截面刚度EiIi、分段长度li及目标弯矩分布，激振力的求解步骤如下：

（1）对于试验叶片，在未添加配重质量情况下，通过传递矩阵法分析试验叶片的模态，并设定试验频率的下限值；

（2）选取适当的激振及配重块添加位置，根据目标弯矩的分布，通过传递矩阵法，求能满足误差δ的匹配质量mj，并确定此时叶片振动系统的固有频率ω.求解的约束条件为叶片振动系统的固有频率高于步骤1设定的下限值，最优目标函数为添加的质量块总和最小。当难以求得满足条件的配重质量时，弯矩包络范围可适量缩小，后续通过激振力调节弯矩包络范围；

（3）对于单点激振，通过传递矩阵法，可计算使得弯矩完全满足误差δ和满足式（15）的激振力；

（4）对于多点激振，还需要考虑各点激振力的分配问题，借助计算机对多个激振力的分配方案寻优，约束条件为满足目标弯矩误差δ和式（16），最优目标函数为弯矩误差δ最小。

3 多点激振加载方案算例

对某型56.5m的叶片进行挥舞方向疲劳加载试验，为了降低阻尼在试验前将叶片尖部截断，剩余的试验叶片长度为48m，根据实际需要，弯矩包络范围设定为8m～32m，弯矩误差δ为+10%，设计单点与多点激振方案，其中多点激振以两点激振为例。两点激振相比于单点，可使用两个质量较小的激振器同时激振。两个激振器的框架质量相同，运动质量可以不同，因此两个激振器的总质量可以不同。根据以上建模方法，可得到单点及两点激振的疲劳加载方案如表1，弯矩包络曲线如图4.将两点激振与单点激振疲劳加载试验方案进行对比，如表2所示。

表1 单点与两点激振方案

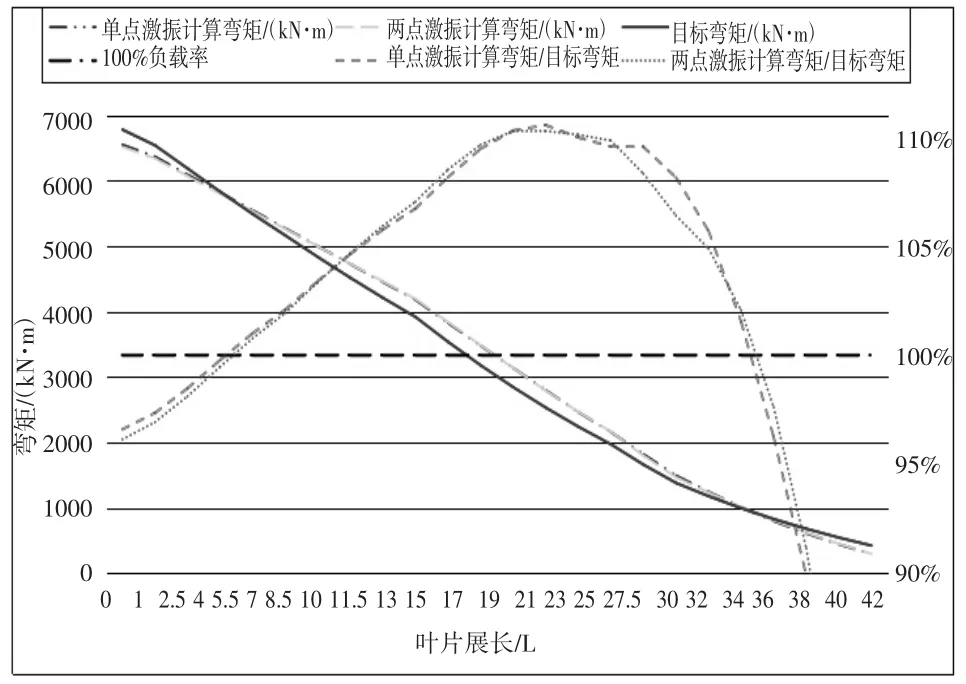
图4 两点激振方案弯矩曲线

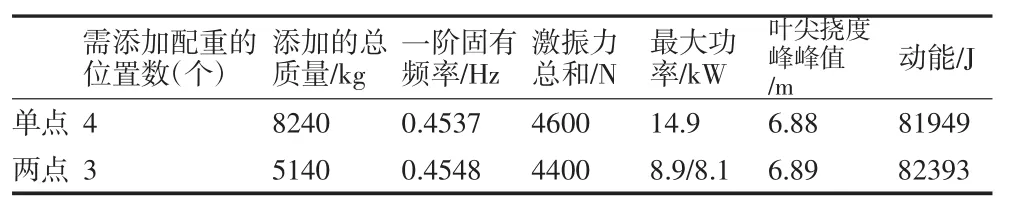
表2 两点激振与单点激振方案对比

4 结束语

本文通过对风机叶片多点疲劳加载系统进行振动模型分析，从激振力和弯矩匹配的角度设计加载方案。通过方案对比，可知叶片多点激振疲劳加载试验，激振力可替代部分质量块的质量来调整弯矩分布，相较于单点激振可灵活调整疲劳试验弯矩分布，使得弯矩更均匀，包络范围增大，且添加的总质量较小，叶片振动系统一阶固有频率升高，有利于增大激振力，减少疲劳试验周期，提高试验平台的利用率。同时随着风机叶片的大型化，多点激振可满足大尺寸叶片疲劳试验的要求。

[1]沈 宏，耿 超，刘 楠，等.国内外风电产业现状及其发展前景[J].河南科技学院学报（自然科学版），2010，38（01）：97-101.

[2]廖高华，乌建中，张 豪.风电叶片双惯性激振疲劳加载耦合振动特性[J].同济大学学报（自然科学版），2017，45（07）：1016-1021.

[3]IEC TS 61400-23-2010，Wind turbines generator systems Part 23：Full scale structural testing of rotor blades[S]．

[4]乐韵斐，骆永云，刘 宇.风电机组叶片疲劳加载试验减阻尼器结构优化设计[J].风能，2017（02）：96-98.