基于Backstepping模糊自适应的四旋翼飞行器控制

张 硕，张学典，秦 敏，陈 征

(上海理工大学光电信息与计算机工程学院，上海200093)

基于Backstepping模糊自适应的四旋翼飞行器控制

张 硕，张学典，秦 敏，陈 征

(上海理工大学光电信息与计算机工程学院，上海200093)

针对四旋翼飞行器轨迹跟踪模型中所受到的外界扰动和参数不确定性等问题，设计了基于模糊自适应反步法的控制策略。在姿态系统中，利用反步法设计控制器，对系统中不确定函数部分采用模糊逻辑系统进行在线逼近。对飞行器运动轨迹进行了跟踪仿真，取得了较为理想的控制效果，验证了该方法的可行性。

模糊控制；四旋翼飞行器；非线性系统；反步法

针对四旋翼飞行控制的研究已有很多经典的控制方法，例如自适应鲁棒方法、反步法、滑模控制方法、人工智能方法、以及优化方法等。反步法(Backstepping)又称反向递推控制。这种方法的主要设计思想是将多维非线性系统分解成多个子系统，并在每个子系统中设计虚拟控制律和Lyapunov能量函数，一直反推到最后一个子系统并完成真正的控制律的设计，通过构造的能量函数来最终保证系统稳定性和动态性能。

1 控制器设计

四旋翼飞行器在飞行时的姿态控制就是对3个姿态角(偏航角ψ，俯仰角θ，滚动角φ)的控制。如图1所示，Rotor1是四旋翼飞行器的头部，Rotor3是尾部，Rotor4和Rotor2分别是左右翼，则ψ角是绕本体坐标系zb轴转动的偏航角，θ角是飞行器头尾部绕本体坐标系yn轴转动的俯仰角，φ角是飞行器左右翼绕本体坐标系xb轴转动的滚转角。选取地面一点Oe作为原点，建立地面坐标系Oexeyeze，选取飞行器质点Ob作为原点，建立本体坐标系Obxbybzb。

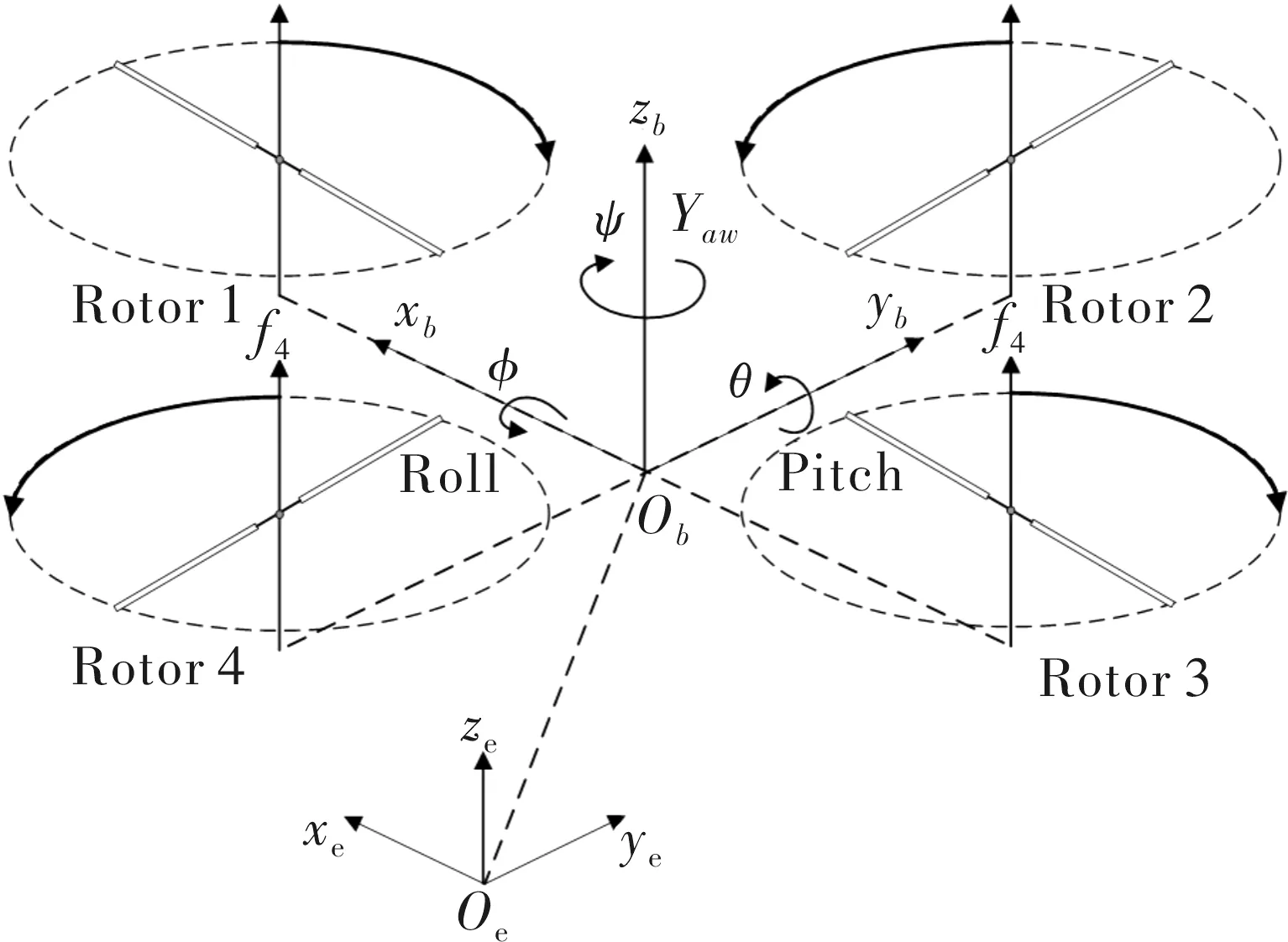
图1 四旋翼飞行器运动姿态

四旋翼运动模型是一个具有6输出(x,y,z,φ,θ,ψ)但只有4个独立输入的动态系统，因此不能同时控制所有参数。可以通过(x,y,z,ψ)得到系统需要的位置信息。一个良好的控制器应该能够移动到指定位置并同时满足俯仰和偏航角的需求，同时保证滚转角的稳定性

(1)

其中输出向量

X=[x11,x21,x12,…,x26]T∈R12

(2)

输入向量

(3)

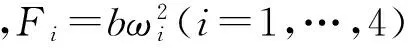
(4)

控制器的主要目标是设计一个输出反馈控制器和参数自适应的规则,所有涉及到的信号闭环系统仍有界,且e1i=x1i,d-x1i,(i=1,…,6)，和期望的一样小。

状态空间模型(1)可以写成

(5)

其中，u5和u6表示俯仰角和x轴运动、滚转角和y轴运动之间的关系

(6)

(7)

(8)

控制器设计分为两步，首先利用跟踪误差来设计虚拟控制率，然后根据系统输出的状态与虚拟控制率的偏差来构建最终的控制器。

步骤1定义追踪误差为

eli=x1i,d-x1i,(i=1,…,6)

选择李亚普诺夫函数

(9)

(10)

步骤2x2i的第二种跟踪误差表示为

(11)

(12)

增强李亚普诺夫函数

(13)

其导数可整理为

(14)

(15)

如果非线性函数fi(x)和gi(x)是已知的，由上式可以容易求出控制律。然而在四旋翼系统中,这些非线性函数难以表示,因此需要引入自适应模糊控制。

2 模糊规则设计

模糊逻辑控制由4部分构成：模糊规则库、推理机、模糊器以及解模糊器。

(16)

x=[x1,…,xn]T∈Rn和y∈R

(17)

(18)

(19)

(20)

模糊基向量表示为

ω(x)=[ω1(x),ω2(x),…,ωN(x)]T

(21)

参数向量为

(22)

模糊逻辑系统可以改写为

y(x|Θ)=ωT(x)Θ

(23)

引理对任意一个在紧集Ωf∈R上有定义的连续函数f(x)，存在常数δ≥0，使得模糊控制系统成立。如

supx∈Ωf|f(x)-ωT=Θ|≤δ

(24)

使得闭环系统稳定的控制输入系统可以表示为

ui(t)=ua,i+ur,i+upd,i(i=1,…,6)

(25)

其中，upd,i=α2ie2i是比例导数项；

(26)

最小模糊近似误差δi可表示为

(27)

可以得出控制律

(28)

控制系统结构如图2所示。

图2 控制系统结构

悬停时控制律

(29)

带入可得

(30)

自适应模糊控制器AFBC(AdaptiveFuzzyBacksteppingControl)系统图如图3所示。

图3 自适应模糊控制器系统图

3 仿真

四旋翼飞行器模型参数如表1所示。

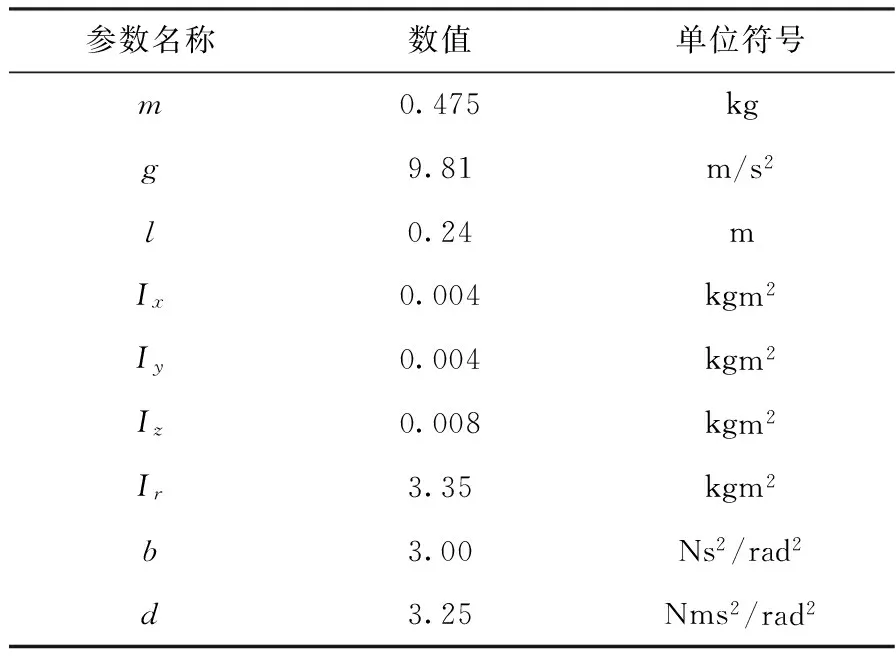
表1 四旋翼飞行器模型参数

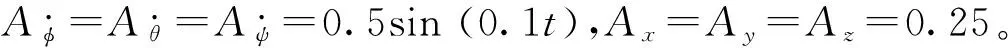
图4 四旋翼飞行器输出跟踪

图5 滚动、俯仰角跟踪

仿真表明，所设计的控制器具有较好的自适应能力，不会因为外界扰动与系统参数不确定的介入而使

控制系统的性能变差，具有较强的鲁棒性。

4 结束语

本文设计了一种基于模糊自适应反步法的控制策略，并通过仿真得出，该控制器在外界扰动和参数不确定性的干扰下，依旧具有良好的轨迹跟踪性能和鲁棒性。

[1]BasriMAM,HusainAR,DanapalasingamKA.Fuzzysupervisorybacksteppingcontrollerforstabilizationofquadrotorunmannedaerialvehicle[C].Grace:InternationalConferenceonIntelligentandAdvancedSystems,2014.

[2]WangQ,StengelRF.Robustnonlinearcontrolofahypersonicaircraft[J].JournalofGuidance,ControlandDynamics,2000,23(4):577-584.

[3] 刘晓华.非线性系统模糊控制研究[D]. 大连:大连理工大学,2002.

[4] 佟绍成.非线性系统的自适应模糊控制[M].北京:科学出版社,2005.

[5] 朱云骥,史忠科.高超声速飞行器飞行特性和控制的若干问题[J].飞行力学,2005,23(3):5-8.

[6] 陈向坚.微型飞行器姿态的只能控制方法研究与实现[D].吉林:吉林大学,2009.

[7] 刘燕斌,陆宇平.基于反步法的高超音速飞机纵向逆飞行控制[J].控制与决策,2007,22(3):313-317.

[8] 王冬来,吕强,刘峰,等.基于L1自适应方法的四旋翼飞行器纵向控制[J].弹道与制导学报,2011,31(3):37-40.

[9] 曾玉龙,赵龙,周建华.基于改进遗传算法的四旋翼无人机参数辨识[J].应用科技,2014,41(3):2-5.

[10] 杨庆华,宋召青.四旋翼飞行器的建模控制与仿真[J].海军工程学院学报,2009,24(5):499-502.

[11] 彭晓华,屠兴汉.求解模糊非线性系统[J].辽宁工程技术大学学报:自然科学版,2010,29(5):776-780.

[12] 郑大钟.线性系统理论[M].北京:清华大学出版社,1990.

[13] 方勇纯,卢桂章.非线性系统理论[M].北京:清华大学出版社,2009.

[14] 魏吉敏.四旋翼飞行器的建模及预测控制研究[D].长沙:中南大学,2013.

[15] 张镭,李浩.四旋翼飞行器模糊PID姿态控制[J].计算机仿真,2014,31(8):73-78.

Adaptive Fuzzy Backstepping Control of Quadrotors

ZHANG Shuo,ZHANG Xuedian,QIN Min,CHEN Zheng

(School of Optical-Electrical and Computer Engineering, University of Shanghai for Science and Technology,Shanghai 200093, China)

This paper presents an adaptive fuzzy control strategy for trajectory tracking of quadrotor unmanned aerial vehicle in the presence of model parameters uncertainties and external disturbances. A fuzzy system is employed to approximate directly a model based control law developed using backstepping techniques. Numerical simulation results are provided to illustrate the good tracking performances of the proposed adaptive control approach.

fuzzy control; aerial quadrotor; nonlinear system; backstepping

2016- 05- 28

张硕(1990-)，男，硕士研究生。研究方向：电气工程。

10.16180/j.cnki.issn1007-7820.2017.02.014

V 249.1;TP273+.4

A

1007-7820(2017)02-054-04