基于细观模型的复合推进剂宏观松弛行为

韩 龙，陈 雄，许进升，周长省，赵 磊

(1.南京理工大学 机械工程学院，南京 210094；2.国营9234厂，合肥 230000)

基于细观模型的复合推进剂宏观松弛行为

韩 龙1，陈 雄1，许进升1，周长省1，赵 磊2

(1.南京理工大学 机械工程学院，南京 210094；2.国营9234厂，合肥 230000)

采用随机算法生成了指定体积分数的复合固体推进剂细观分析模型。通过有限元方法及对细观场量的均匀化处理，对复合固体推进剂不同随机分布、颗粒尺寸分布及在不同应变水平下的力学响应进行了数值模拟，研究了颗粒分布随机性及颗粒大小对推进剂松弛性能的影响，并预测推进剂在宏观上的松弛行为。类比于时间温度等效原理，建立了复合推进剂时间-应变等效，并通过该原理将各应变水平松弛曲线沿时间轴平移，得到复合推进剂的预测松弛模量主曲线，预测结果与试验结果吻合较好。通过该方法生成的细观分析模型，可直观描述细观结构损伤对推进剂松弛力学性能的影响，并可在一定程度上预测不同配比方案复合推进剂的宏观松弛行为，对复合固体推进剂的配方设计及固体火箭发动机装药设计具有一定的指导意义。

复合推进剂；细观模型；界面脱粘；粘接单元；粘弹性

0 引言

固体火箭发动机作为火箭武器的动力提供者，对保障火箭武器的作战性能及生存能力具有重要作用。固体火箭发动机的设计一般是依据固体火箭总体部门的设计性能要求，选取满足推进性能及力学性能要求的推进剂类型及装药方式。根据实际应用过程中的固体火箭发动机的工作环境及载荷情况，对装药结构初始方案进行结构完整性分析，以确定所选推进剂方案的适用性及可靠性。推进剂力学性能达不到预期设计要求时，则需要对推进剂配方加以改进。由于整个火箭发动机的设计过程依赖于推进剂及结构设计两方面的相互制约和协调，因而对推进剂配方做出的每次细微调整，都会导致耗费较大的人力及物力来重新校订整体结构性能，改进周期长，严重制约着设计任务进展的时效性。

复合固体推进剂在构成上为多相组分体系，其组成为粘合剂及增塑剂等构成的连续相和由氧化剂、金属固体颗粒等组成的分散相。复合推进剂的结构组成，决定了其对于外界载荷作用会产生较为复杂的力学响应。一般工程应用中，均将复合推进剂在宏观上视为一种粘弹性的均质体系，通过唯象学方法，引入损伤来描述推进剂的非线性力学响应[1-3]，此类方法虽在一定程度上能满足对于复合推进剂力学行为的分析要求，但很难描述推进剂在细观尺度上的性能劣化及破坏过程及细观组分对推进剂宏观力学性能的影响，且在配方研发过程中，只能对由初始配方生产出的推进剂样品进行宏观上的力学试验方能获取所设计推进剂方案的力学性能，若不满足设计要求，则须返回修正，进而根据更改后的配方再次进行相关试验，如此循环，造成极大的人力、物力及时间消耗。因此，在细观尺度上，对复合固体推进剂的力学性能进行定性及定量分析，将成为解决上述问题的一种极其有效的途径。通过推进剂细观尺度上的数值研究，有效获取推进剂的宏观力学特性，对提高固体推进剂配方研发及火箭发动机的装药结构设计效率具有重要现实意义。

对于多相材料的细观力学研究方法，主要分为解析法和数值法两类。解析法即通过细观力学方法，在一定简化及假设基础上，分析材料的细观应力应变关系，从而导出材料的宏观力学属性，较成熟的理论方法主要有：Eshelby等效夹杂理论[4]、自恰理论[5]、Mori-Tanaka方法等。其中，Mori-Tanaka方法由于计算简单，且一定程度上能够计及填充颗粒之间的相互作用，已被众多学者广泛用于材料的细观力学研究[6-7]。但由于细观解析法只能考虑较少因素，预测精度有限，使其使用范围受到一定限制。数值方法是伴随计算机发展而逐渐开展起来的求解材料细观问题的一种主要方法，主要分为有限元法及通用元胞法。该方法通过多相材料夹杂尺寸尺度范围内的细观应力应变关系来反映材料在宏观上的力学属性，可考虑细观各因素对材料宏观性能的影响，计算精度较高，适用范围广。Matous等[8]、Inglis等[9]等研究了基于胞元结构的颗粒界面脱湿的粘聚区理论及损伤演化过程。Matous等[10]依据分子动力学算法，建立了典型推进剂细观代表性体积单元，并对颗粒与基体之间的损伤及脱粘对推进剂宏观力学行为的影响进行了研究。Tan等[11]对高能材料颗粒与基体之间的粘接性能进行了研究，建立了颗粒与基体之间的界面的内聚法则。吴丰军等[12]NEPE推进剂/衬层粘接界面细观力学性能进行了研究，提出NEPE推进剂/衬层粘接界面失效模式。职世君等[13]采用分子动力学方法对高填充比复合固体推进剂细观模型进行建模，给出了复合固体推进剂颗粒粒径、位置的随机分布对固体推进剂细观损伤及宏观力学性能的影响。赵玖玲等[14]利用蒙特卡洛随机采样方法建立了推进剂细观胞元模型，研究了颗粒体积分数对推进剂初始模量的影响。Chang等[15]采用双线性粘聚区本构模型来反映界面的力学响应特征，分析了细观粘接界面的损伤与失效规律，研究了不同界面特性对力学行为的影响规律。张建伟等[16]依据有限元理论及均匀化方法，通过有限元细观计算应力应变场结果，有效地预测了复合固体推进剂的宏观松弛模量。

以上文献主要集中于研究复合推进剂细观结构体积分数、颗粒大小分布，颗粒基体之间粘接性能对推进剂宏观力学行为的影响，以及推进剂细观结构脱粘损伤过程的数值模拟，但对于推进剂细观结构松弛力学行为的研究较少。

本文通过建立复合推进剂细观分析模型，对不同应变水平下复合推进剂的松弛行为进行了数值仿真，将细观应力应变场进行局部均匀化，以得到材料在宏观上的松弛模量曲线，通过将不同应变水平松弛曲线在时间轴的平移，预测了推进剂在宏观上的松弛模量主曲线，从而实现了由细观结构预测推进剂宏观松弛行为的目的。

1 分析模型及计算方法

1.1 复合推进剂各组分材料属性参数

复合推进剂主要由粘接剂体系及固体填充颗粒体系所组成，对于推进剂中AP、Al及HMX等颗粒，具体弹性模量及泊松比数值可通过文献[15]获取，由表1给出。为便于有限元计算，将粒径较小的固体填充颗粒与粘合剂视为是一种均匀化的复合基体，目前较常用的实现途径主要是Mori-Tanaka及其衍生而来的各种等效方法，但此类方法对于具有粘超弹特性的基体材料难以提供较为满意的等效处理结果。为了描述复合固体推进剂的超弹性及近似不可压特性，可选用Neo-Hookean超弹模型来实现。式(1)给出了该模型的应变能描述[17]：

(1)

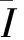
初始剪切模量μ0和初始体积模量K0可由2个温度相关的参数来确定：

(2)

对于平面应变问题，综合考虑到材料的近似不可压性及材料在有限元计算中高度约束的边界条件下的计算可行性，需给予材料一定的可压缩性，可简单的以材料未受载时的体积与剪切模量的比值，作为描述材料相对可压缩性的泊松比数值：

(3)

为了获取模型中的基体与小颗粒所组成混合物的材料参数，选用数值均匀化方法来实现，具体流程可见文献[18]，基于Abaqus有限元平台计算拟合，可得参数数值分别为：C10=1.23，D1=0.001 5。

复合固体推进剂基体的粘弹性可由基体胶片的应力松弛试验，根据试验结果，由Prony级数形式拟合得出，如图1所示。有限元建模时，须将各阶参数做归一化处理后，赋给对应的基体材料。

表1 复合推进剂各组分材料参数

1.2 颗粒填充模型

复合推进剂的细观界面是粘合剂基体固化交联反应中与颗粒经复杂的化学物理作用而形成的，颗粒填充比例高，图2给出了复合推进剂拉伸断面的显微图。从图2可看到，推进剂中固体颗粒的含量较高，断面中存在较多的完整大颗粒固体及颗粒拔出后的凹坑，说明推进剂在受载过程中主要沿较大颗粒表面开始破坏，而小颗粒与基体之间混合均匀，主要起增强粘合剂基体刚度的作用，故为了保证建立有限元模型的计算收敛性及减少分析计算量，本文在模型建立中，主要考虑较大颗粒与基体所组成的代表性细观结构，具体颗粒尺寸配比为颗粒尺寸呈双峰分布，大小颗粒的平均直径分别为20 μm、100～300 μm，颗粒的体积分数约为62%。采用随机连续吸附算法[19]生成颗粒随机堆积模型，颗粒尺寸服从正态分布。

1.3 粘接界面模型

对于细观模型中颗粒相及基体之间的粘接性能，选用内聚力模型可实现较好模拟。即认为材料细观结构在受载过程中，颗粒与基体界面会经历一个弹性—软化—破坏的过程，初始受载阶段，由于界面变形较小，应力随张开位移值线性增长，当张开位移增长至临界位移值时，界面开始出现损伤，进而导致界面力学性能劣化，界面应力随位移值逐渐减小，直至张开位移达到失效位移时，界面彻底失效，此时基体与颗粒间完全分开，无法再传递载荷。本文选用应用较广的双线性模型，界面本构由式(4)给出：

(4)

式中Tmax为界面强度；K1和K2分别为界面的弹性模量及软化模量；δ0为损伤临界位移；δf为失效张开位移。

细观界面参数的获取手段目前还尚未取得突破，主要还是基于宏观试验研究及经验性的预估。Tan等[11]在对含能材料的研究中发现，高体积分数含能材料的细观界面强度与宏观强度数值较为接近，故可直接取常温下复合推进剂的宏观试验数据作为细观分析时的界面强度，一般取为0.5～1.0 MPa；界面模量关乎数值计算时的收敛性，较小的界面初始刚度，会导致计算时材料结构局部刚度不足，引发不必要的变形，增加计算代价；反之，较大的初始刚度值则会导致计算时出现应力震荡，影响最终的仿真结果[20]。界面模量及断裂能根据文献[15]，分别取为K=500 MPa/mm，G=2～8 J/m2。

粘聚区界面尚未发生损伤前，界面为线性响应，当界面承载达到损伤起始标准时，便会以一定的形式开始损伤，造成界面力学性能的劣化，如图3所示，对于有限元计算，界面应力可由式(5)表述：

(5)

式中t、n分别表示切向与法向；Knn和Ktt为弹性刚度；粘接界面应变εn和εt可由界面位移与界面单元的初始厚度之比得出；D为描述界面损伤程度的变量，D=0时，对应界面的初始无损伤阶段，D=1时，则说明界面已无任何承载能力。

对于复合推进剂中球形填充颗粒的圆弧界面，界面载荷状态相对于纯法向及切向受载情况下更复杂，界面当前的载荷状态由当前切应力及法向应力所共同确定。在计算中，有可能出现尚未达到界面强度时界面就已经进入损伤软化阶段。因此，须选用混合模式以判断颗粒与基体间界面的损伤起始点。在此，选用二次应力失效准则：

(6)

式中 <>为Macaulay括号，其定义为=1/2(x+|x|)，以描述法向压缩载荷下不会导致界面单元损伤的产生。

1.4 单元划分

在有限元分析中，除平面应力问题外，须采用杂交单元来模拟不可压缩材料(泊松比为0.5)或近似不可压缩材料(泊松比大于0.475)的响应。对于不可压缩材料，其在受载过程中，体积始终保持恒定，不会随应力应变状态而发生改变，从而导致有限元计算时无法利用节点处的位移插值函数来有效得到单元的压应力，而杂交单元毋须通过节点位移插值，仅通过自身设有的额外自由度即可直接获取单元的压应力，偏应力及偏应变的获取则仍依赖于节点的位移场计算。因此，对代表性体积单元进行网格划分时，推进剂基体材料采用平面应变4节点四边形线性积分的杂交单元CPE4H，填充颗粒采用CPE4。大变形情况下，界面处通过定义摩擦罚函数值来施加通用接触算法，以防止基体及颗粒在界面单元处发生相互渗透，基体与颗粒之间插入粘接单元(Cohesive element)以模拟颗粒与基体界面的粘接特性，无载荷时粘接单元具有零或指定厚度，且在Abaqus中粘接单元只适用于扫略网格，网格扫略路径指定为沿径向。由于粘接单元收敛较不易，计算时可设置较小的初始载荷步，并对粘接单元设定一定的粘性，以保证计算的可行性。

1.5 复合推进剂模量预测的有限元方法

利用有限元方法预测复合材料固有属性参数时，首先需对代表性体积单元施加周期性边界条件，以满足宏观上的连续均质假设，周期边界条件可表示为

(7)

式中L为RVE(Representative Volume Element)尺寸；u1和u2为加于边界上的位移载荷。

但由于周期边界条件须在周期性网格的基础上方能实现，在实际应用中较不便，本文选用均匀位移边界条件，如图4所示。均匀位移边界条件下，代表性体积单元在受载变形过程中，各边保持平直，图中虚线为RVE变形后边界位置所在。文献[21]的研究表明，均匀位移边界与周期性边界条件施加下的计算结果存在一定差异，但两者差值会随代表性体积单元的尺寸增加而逐渐趋于零值。

平面应变问题下，通过有限元方法计算得到的局部细观应力、应变场，须进行局部细观场的平均方能获取材料在宏观上的力学表象。对于复合推进剂细观RVE而言，细观应力σij和应变εij，对体积进行平均，可得平均应力和平均应变：

(8)

2 计算结果及讨论

2.1 颗粒随机分布对推进剂松弛性能的影响

为研究推进剂细观结构中，颗粒随机分布性对推进剂松弛性能的影响，应用随机连续吸附算法，对推进剂进行4次建模，如图5所示。

分别对不同随机性得到的模型进行仿真计算，根据前述的细观场平均方法，将有限元计算出的细观应力及应变，均匀化处理后，可据式(9)得出复合推进剂宏观松弛模量为

(9)

计算结果由图6给出，不同模型的计算结果曲线较为接近，可认为在体积分数及颗粒平均尺寸保持一定的情况，颗粒分布随机性对推进剂的松弛性能影响较小，同时也可反映出，本文的模型可在一定程度上反映推进剂的在宏观上的结构均匀性。

2.2 颗粒尺寸大小对推进剂松弛性能的影响

为研究颗粒尺寸对复合推进剂宏观松弛性能的影响，保持填充颗粒体积分数不变，改变填充颗粒的尺寸大小，利用随机算法进行3次建模。图7给出了不同于图4的另外2个模型，3个模型中颗粒的平均尺寸分别为45、55、75 μm。

对3个模型在0.2应变水平下分别进行仿真计算，得到的松弛模量曲线结果见图8。

由图8可看出，体积分数不变的前提下，颗粒尺寸较大时，推进剂宏观松弛模量较小，而颗粒尺寸较小时，对应的宏观松弛模量较大。这是因为在受载过程中，由于大颗粒更易与基体之间发生脱粘，从而导致推进剂松弛模量偏低，小颗粒与基体间相对而言不易发生脱湿，对应的推进剂宏观松弛模量会偏高。

2.3 不同应变下细观松弛计算结果

对所研究的复合固体推进剂细观模型施加指定的轴向定应变载荷(应变值为0.05，0.08，0.1，0.2，0.3，

0.4)，其中应变值由位移载荷与加载方向上RVE的边长之比得到，利用有限元法计算模型的应力松弛响应。图9为复合固体推进剂细观代表性体积单元模型在100 s应力松弛时的应力、应变分布。

从不同应变下的应力松弛计算结果可看出，在低应变载荷下，基体与颗粒之间粘接完好，大颗粒周围出现较大的应力数值，随着加载应变的增加，颗粒与基体之间开始出现明显的脱粘现象，不同应变下，颗粒与基体的脱粘程度不一，且脱粘首先发生在大颗粒与基体之间，较大颗粒与基体完全脱粘后，较小粒径颗粒与界面的界面性能开始降低，直至完全脱粘。另外，颗粒较为密集的区域，局部应力及应变较大，说明颗粒基体的脱粘加剧了推进剂局部力学性能的劣化，进而导致局部破坏进程加剧。

复合推进剂不同应变水平下的松弛模量计算结果见图10。从图10可看出，不同应变水平下(对应不同的颗粒基体脱粘程度)，推进剂的松弛曲线数值大小不同但整体趋势一致，且高应变载荷下，推进剂的松弛模量数值较低，而对应低应变载荷，推进剂的松弛模量数值较高，说明颗粒与基体之间的脱粘破坏，仅影响推进剂的松弛模量大小(特别是初始松弛模量)，而不影响其松弛特性。另外，从图10可看出，在松弛应变值较小时(0.05～0.2)，应变的增加对松弛模量的影响较大，而当应变水平较高时(0.2～0.4)，随着应变水平数值增加，松弛模量数值变化较小。这是由于应变水平较低时，随着应变值增加，颗粒与基体脱粘较严重，对推进剂整体松弛性能较大，而随着应变达到一定值后，大部分颗粒都已与基体脱粘，仅有剩余较少的小颗粒与基体之间粘连，对推进剂松弛行为的影响较小。

2.4 推进剂松弛主曲线预测

对于图10中的不同应变水平松弛曲线，可参照时温等效原理，认为应变水平同温度一样对材料的自由体积产生相似的影响，从而根据自由体积理论，导出与时温等效类似的时间-应变等效原理，即

(10)

式中φε为应变移位因子；ε0为参考应变；C1和C3为材料常数，可通过非线性拟合得出。

根据时间-应变等效，复合推进剂在不同应变水平下的应力松弛模量曲线可沿着时间轴平移而叠合在一起，构成某一参考应变水平下的松弛模量主曲线。为了验证分析结果及预测的松弛模量主曲线的准确性，对复合推进剂试件进行1 800 s的真实应力松弛试验，并将试验结果与有限元计算预测曲线相对比，如图11所示。从图11可看出，试验结果与预测结果较一致，但也存在一定偏差。对于差值产生的原因，主要归结如下：

(1)鉴于固体推进剂真实细观结构的复杂性，本文采用的细观分析模型与真实复合推进剂的细观结构之间存在一定差异，无法完美体现推进剂在细观结构上的局部不均匀性；

(2)颗粒与基体之间的界面单元尚未加入率相关性，加载及松弛过程中，界面单元没有对应的粘弹性响应；

(3)基体材料尚未引入损伤演化及破坏准则，无法考虑基体材料在加在过程中的力学性能劣化等因素，故整体分析计算结果较真实情况有所偏差。

上述问题及不足也是本文后续研究工作亟待解决的方向。

3 结论

(1)建立和实现了定应变载荷下复合推进剂细观松弛响应的数值模拟，得到了颗粒与基体间界面损伤形核及扩展过程中非均匀应力应变分布及对应的松弛模量曲线。

(2)细观结构中颗粒的随机分布性不影响推进剂的宏观松弛行为，而保持颗粒体积分数不变的前提下，颗粒的尺寸大小会影响推进剂宏观松弛行为，较大的颗粒尺寸会导致较低的松弛模量，较小的颗粒尺寸则对应较高的松弛模量。

(3)颗粒与基体之间的脱粘程度仅影响松弛模量大小，而不影响推进剂整体的松弛特性，高应变、脱粘程度高时，对应松弛模量数值较小；低应变、脱粘程度低时，对应松弛模量数值较大。

(4)通过有限元分析局部应力及应变场的均匀化，得到推进剂在宏观上的松弛模量曲线，并通过时间-应变等效，得到了预测推进剂宏观松弛模量主曲线，与实际松弛试验结果吻合较好。

[1] 孟红磊,鞠玉涛.含损伤非线性粘弹性本构模型及数值仿真应用[J].固体火箭技术,2012,35(6): 764-768 .

[2] 姚东,张光喜,高波.考虑应力状态的HTPB/AP推进剂含损伤热-粘弹性本构方程研究[J].固体火箭技术,2014,37(4): 496-499 .

[3] Xu J,Chen X,Wang H,et al.Thermo-damage-viscoelastic constitutive model of HTPB composite propellant[J].International Journal of Solids and Structures,2014,51(18): 3209-3217.

[4] Eshelby J D.The elastic field outside an ellipsoidsal inclusion[J].Proceedings of the Royal Society of London: Series A Mathematical and Physical,1959,252(1271): 561-569.

[5] Hill R A.A self-consistent mechanics of composite materials[J].Journal of the Mechanics and Physics of Solids,1965,13(4): 213-222.

[6] Tanaka F,Okabe T,Okuda H,et al.The effect of nanostructure upon the deformation micromechanics of carbon fibres[J].Carbon,2013,52: 372-378.

[7] Mortazavi B,Baniassadi M,Bardon J,et al.Modeling of two-phase random composite materials by finite element,Mori-Tanaka and strong contrast methods[J].Composites Part B: Engineering,2013,45(1): 1117-1125

[8] Matous K,Geubelle P H.Finite element formulation for modeling particle debonding in reinforced elastomers subjected to finite deformations[J].Computer Methods in Applied Mechanics and Engineering,2006,196(1): 620-633.

[9] Inglis H M,Geubelle P H,Matous K.Cohesive modeling of dewetting in particulate composites: micromechanics vs.multiscale finite element analysis[J].Mechanics of Materials,2007,39(6): 580-595.

[10] Matous K,Inglis H M,Gu X,et al.Multiscale modeling of solid propellants: From particle packing to failure[J].Composites Science and Technology,2007,67(7): 1694-1708.

[11] Tan H,Liu C,Huang Y,Geubelle P H.The cohesive law for the particle/matrix interfaces in high explosives[J].Journal of the Mechanics and Physics of Solids,2005,53(8): 1892-1917.

[12] 吴丰军,彭松,池旭辉.NEPE推进剂/衬层粘接界面细观力学性能/结构研究[J].固体火箭技术,2010,33(1): 81-85.

[13] 职世君,孙冰,张建伟.基于表面粘结损伤的复合固体推进剂细观损伤数值模拟[J].推进技术,2013,34(2): 273-279.

[14] 赵玖玲,强洪夫.基于粘附功的复合推进剂AP /基体界面损伤宏细观仿真[J].固体火箭技术,2011,34(5): 614-622.

[15] Chang W,Ju Y,Han B,et al.Numerical Simulation of Particle/Matrix Interface Failure in Composite Propellant[J].Journal of China Ordnance,2012,8(3): 146-153.

[16] 张建伟，职世君，孙冰.基于细观颗粒夹杂模型的复合固体推进剂松弛模量预测[J].航空动力学报,2013,28(10): 2370-2375.

[17] Rivlin R S.Large elastic deformations of isotropic materials.I.Fundamental concepts[J].Philosophical Transactions of the Royal Society of London.Series A,Mathematical and Physical Sciences,1948,240(822): 459-490.

[18] Guo Z,Shi X,Chen Y,et al.Mechanical modeling of incompressible particle-reinforced Neo-Hookean composites based on numerical homogenization[J].Mechanics of Materials,2014,70(3):1-17.

[19] Segurado J,Llorca J.A numerical approximation to the elastic properties of sphere-reinforced composites[J].Journal of the Mechanics and Physics of Solids,2002,50(10): 2107-2121.

[20] Turon A,Davila C G,Camanho P P.An engineering solution for mesh size effects in the simulation of delamination using cohesive zone models[J].Eng.Fract.Mech.,2007,74(10): 1665-1682.

[21] Pierard O.Micromechanics of inclusion-reinforced composites in elasto-plasticity and elasto-viscoplasticity：modeling and computation[D].University Catholique de Louvain,2006.

(编辑：刘红利)

Relaxation behavior of composite propellant based on meso-mechanical model

HAN Long1,CHEN Xiong1,XU Jin-sheng1,ZHOU Chang-sheng1,ZHAO Lei2

(1.College of Mechanical Engineering,Nanjing University of Science and Technology,Nanjing 210094，China； 2.State-operated 9234 Factory,Hefei 230000，China)

Adsortion algorithm was used to generate the meso-scale analysis model of composite propellant with specified volume fraction.The numerical simulation of the mechanical response of composite propellant under series strain levels was conducted with the commercial FEA software Abaqus/Standard.The effect of spatial distribution and particle size distribution on the relaxation behaviour of composite propellant was studied.The simulation results were used to further obtain the prediction of macroscopic relaxation behavior of composite propellant with the homogenization method.The time strain equivalence principle was derived and the master relaxation curve was generated by horizontal translating along the time axis based on the established equivalence principle.The estimated result shows good agreement with the experimental results.The effect of meso-structure damage on the relaxation behavior of composite propellant can be visual described by the present finite element model.The results prove that the approach has practical significance of grain design of solid rocket motor as well as formula design of solid propellant.

composite propellant；meso-model；interface debonding；cohesive method zone；viscoelastic

2015-01-27；

2015-04-01。

江苏省自然科学青年基金(BK20140772)。

韩龙(1988—)，男，博士生，研究方向为装药结构完整性分析。E-mail:longh_xdrive@126.com

许进升，博士，研究领域为装药结构完整性分析。E-mail:xujinsheng@njust.edu.cn

V512

A

1006-2793(2017)01-0052-08

10.7673/j.issn.1006-2793.2017.01.009