可压缩流涡流冷壁发动机数值模拟
党进锋,郜 冶,刘平安
(哈尔滨工程大学 航天与建筑工程学院,哈尔滨 150001)
可压缩流涡流冷壁发动机数值模拟
党进锋,郜 冶,刘平安
(哈尔滨工程大学 航天与建筑工程学院,哈尔滨 150001)
为深入探索入射倾角、入射压降、发动机圆柱段长度等参数与涡流冷壁发动机内双向涡流结构特征量之间的内在关系,以三维物理模型为基础,进行了可压缩流涡流冷壁发动机冷流数值模拟。在前期湍流模型选择中,比较了RSM模型、带旋流修正RNGk-ε模型、RNGk-ε模型3种模型的可信度,从准确度和经济性两方面综合考虑选择带旋流修正RNGk-ε模型作为计算模型。研究发现,切向速度及最大切向速度均随入射倾角的增大而减小,随入射压降增大而增大,随长径比的增大而减小。不同入射倾角、不同入射压降、不同长径比下,整个发动机内最大切向速度的无量纲径向位置均恒定在0.19附近。对于不同长径比工况,长径比为1.0时,最大切向速度从发动机顶端到入射口附近逐渐增大,长径比为1.5时,最大切向速度从发动机顶端到入射口附近先增大、后减小。切向速度及最大切向速度的轴向衰减率维持在3%以内。无量纲涡幔半径从发动机顶端开始线性增大到入射口附近,变化范围为0.71~0.82。入射倾角相同时,随入射压降的增大,燃烧室长径比对最大切向速度大小的影响将随之增大。
涡流冷壁发动机;可压缩;湍流模型;入流条件;长径比;数值模拟
0 引言
涡流冷壁发动机(Vortex Combustion Cold-Wall Chamber,VCCWC)由于内部强旋转流动的存在,数值计算难度相较于无旋转或弱旋转流动增大许多,其计算所需的湍流模型、网格分布、数值方法等均有别于普通流动。因此,数值计算研究进展非常有限。美国Majdalani等针对涡流冷壁发动机内双向涡流进行了大量理论研究[1-3],其研究成果对于验证涡流冷壁发动机可行性、认识双向涡流结构特点等方面具有非常重要的意义。其与Orbital科技公司Chiaverini等人所做的涡流冷壁发动机燃烧实验,为涡流冷壁发动机研究奠定了基础[4]。在Majdalani与Chiaverini等人带动下,国内从2010年左右,也开始对涡流冷壁发动机进行了相关理论、实验与数值计算研究。孙得川等[5]通过理论推导,得到涡流冷壁推力室传热模型,通过数值计算研究,指出一次进气有利于燃料与空气的掺混燃烧[6],文献[7]通过实验研究了双向涡流速度分布规律。李家文、俞南嘉等人在文献[8-9]中,通过实验和数值计算,验证了涡流冷却技术的可行性,在文献[10]中指出,冷却剂喷嘴倾斜一定角度,可改善内涡强度,改进燃料掺混、提高燃烧效率。文献[11]中采用三维全尺寸可压缩流体模型,验证了推力室内存在同轴反向的双层涡旋结构,并指出在后续研究中,有必要明确涡旋速度场环形区域对推力室燃烧效果的具体影响;文献中同时还指出,有必要针对涡旋来流条件、圆柱段几何尺寸、燃料喷注方式等,开展优化推力室结构的仿真研究。可看到,现阶段对于VCCWC的研究,仍停留在可行性验证与定性的规律描述上。因此,针对VCCWC内双向涡流结构特征影响因素及其定量描述的研究就显得尤为迫切。
本文在文献[11]研究基础上,针对文献[11]中提出的涡旋来流条件、圆柱段几何尺寸等内容,进行了三维可压缩流数值模拟研究,所得结论对于深入认识VCCWC内涡流结构随模型几何尺寸及来流条件的变化具有重要作用,对于未来VCCWC设计具有一定指导作用。
1 物理模型、计算工况及边界条件
由于VCCWC具有轴对称特征,文中采用与文献[8]中相同的三维周期性边界,取全模型周向1/6作为计算模型,该1/6模型上周向均布2个入射口,即全模型为12个入射口。本文为亚音速冷流数值模拟,流动未达到临界状态,因此采用收缩喷管形式,模型具体尺寸如图1所示。图2为三维模型网格示意图。
表1为本文中所完成的16种计算工况。发动机圆柱段长度L分别为100 mm和150 mm,对应发动机长径比αL=L/D分别为1和1.5,发动机顶部无量纲轴向位置记为α=0,则切向入射处无量纲轴向位置分别为α=1和α=1.5。无量纲径向位置记为β=r/R,则壁面处β=1,对称轴处β=0。入射倾斜角θ从0°增大30°,入射压降Δpin分别为41 700 Pa和62 550 Pa,操作压力为101 325 Pa,出口为压力出口,计算工质为300 K可压缩理想气体。
2 计算可信性验证
2.1 湍流模型选择及可信性验证
文献[6]中指出,求解涡流冷壁推力室内的强旋转流动,采用RSM(雷诺应力)模型较台适,文献[8]采用RNGk-ε模型进行了燃烧数值模拟,文献[11]采用RNGk-ε模型,并激活旋流修正进行了燃烧数值模拟, Fang在文献[12]中结合Standardk-ε模型和RSM模型数值计算,模拟了VCCWC冷流与燃烧过程。笔者在前期研究中也发现,RSM湍流模型相较于两方程模型具有一定优势。两方程模型中,RNGk-ε模型由于可加入旋流修正,大大改善了其旋转流动数值计算的准确性。本文在选择计算所采用的湍流模型时,对RSM、RNGk-ε模型、带旋流修正的RNGk-ε模型进行了比较,从数值结果准确性与计算经济性两方面,综合决定最终所采用的湍流模型。计算中,压力-速度耦合算法为SIMPLE算法,梯度差分采用G-S节点基格式,压力差分采用二阶格式,其余通量差分均为二阶迎风格式,计算采用Ansys Fluent 11.0软件。
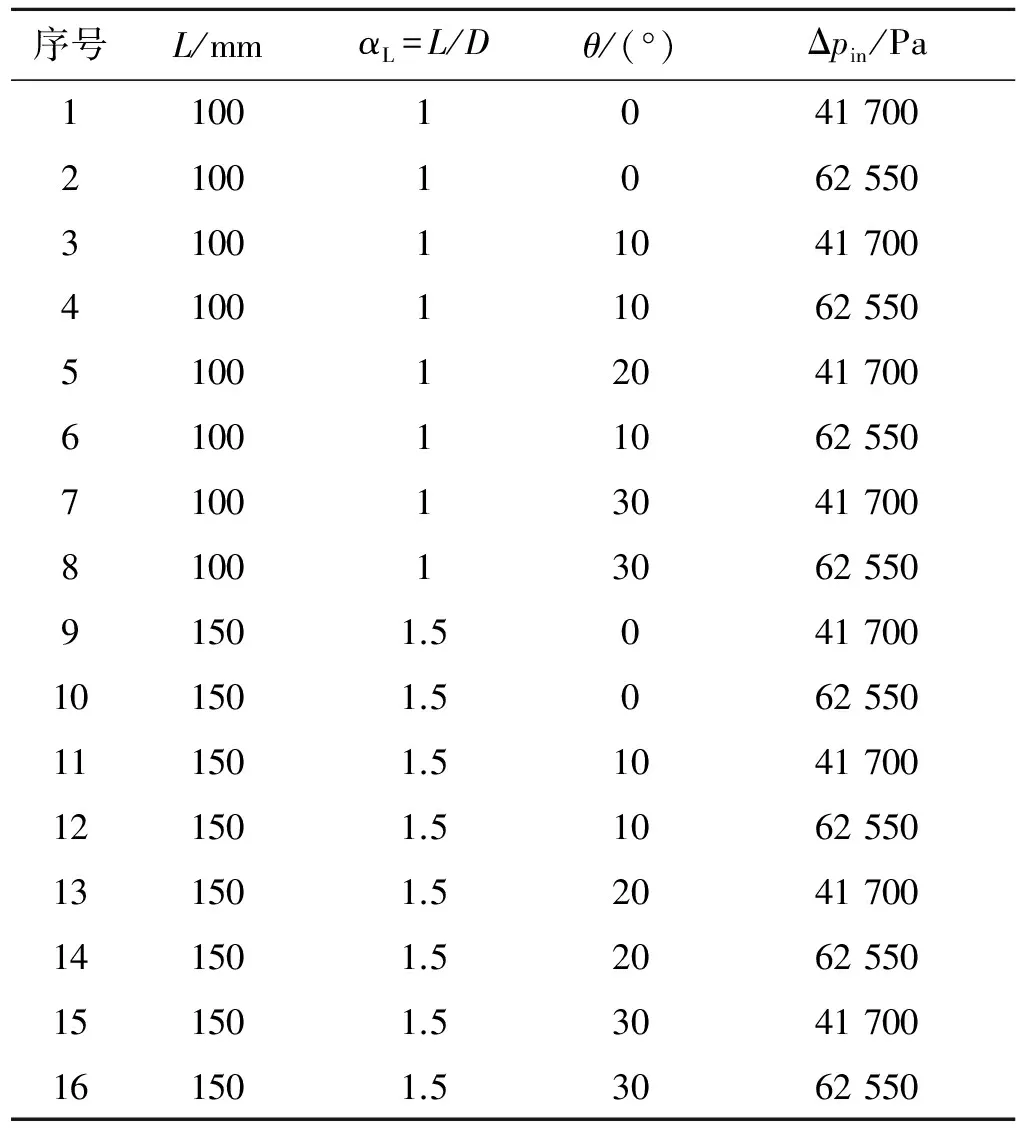
表1 计算工况
图3为3种验证模型计算所得压力曲线与文献[13]中实验数据对比曲线,图4为3种验证模型计算所得压力云图。从图3可看到,各湍流模型计算所得燃烧室内压力值变化趋势并不相同。实验数据在0.6<β<1.0范围内,压力下降缓慢,β<0.6后,压力下降速度逐渐增大。3种模型中,RSM模型曲线与实验数据吻合度最好,其次是带旋流修正的RNGk-ε模型,不带旋流的RNGk-ε模型相差较多。图4分别为RSM模型、带旋流的RNGk-ε模型及不带旋流的RNGk-ε模型压力云图。从图4同样可看到,3种模型所得压力云图变化规律与图3的曲线相同,二者相互验证。
结合图3、图4结果可知,RSM湍流模型精确度最高,与实验值吻合最好,其次为带旋流修正的RNGk-ε模型,所得压力变化趋势与实验结果相一致,关键位置处误差在可接受范围内,不带旋流修正的RNGk-ε模型则与实验结果相差较远。从经济性角度出发,RSM模型相较于带旋流修正的RNGk-ε模型,增加了约1倍的计算量,且RSM模型的精细化使其难以收敛。因此,综合考量准确度与经济性因素,最终选择带旋流修正的RNGk-ε湍流模型作为计算模型。
2.2 网格依赖性验证
图5、图6分别为不同网格数计算所得的压力、切向速度分布曲线。3种网格mesh-1、mesh-2、mesh-3网格数分别为707 362、451 938、207 816,分别对应于致密网格、中等网格及稀疏网格,计算所用湍流模型为2.1节结论中所得带旋流修正的RNGk-ε湍流模型。
从图5可看到,不同网格所得压力径向分布基本重合,变化趋势以及关键位置处与实验数据吻合得非常好。图6为不同网格所得切向速度vt径向分布,3种网格所得vt分布在整个半径方向基本重合。
综合图5、图6中结果可知,所选湍流模型及计算设置对网格的依赖性非常低,即致密网格、中等网格以及稀疏网格均可得较可信的计算结果。但同样考虑到计算精确度和经济性因素,致密网格计算较慢,稀疏
网格捕捉流场信息较少。因此,综合考虑选择中等网格设置作为最终计算网格。
3 计算结果及讨论
通常研究者对VCCWC中特别关心的流场信息包括压力p分布、轴向速度va分布及切向速度vt分布。从第2章中看到,VCCWC内p分布易于常规固体或液体火箭发动机,其推力计算有别于常规火箭发动机[4,9,11]。va分布决定了涡幔半径rm的大小,对VCCWC燃烧及冷壁作用均有重要意义。vt分布决定了燃料与氧化剂的掺混程度及压力梯度力与离心力所形成的力学平衡。
3.1 入射倾角θ对内流场涡结构影响
入射倾角数值研究中,Δpin=41 700 Pa,αL=1.5。计算所得α处vt径向分布曲线见图7。从图7可见,vt曲线在0<β<0.05范围内接近0 m/s,从β=0.05开始,vt迅速增大,在β=0.19左右达到vt,max,随后逐渐减小,靠近β=1时,迅速减小为0 m/s,以匹配无滑移壁面条件,该速度分布曲线与Majdalani所得理论曲线变化趋势相一致[13-17]。随着θ的增大,vt及vt,max均减小,说明入射倾角θ的增大,减小了来流总动量中切向动量比例。θ=0°与θ=10° 2条曲线基本重合,当θ>10°时,vt及vt,max均迅速减小,说明vt减小的速率随着θ的增大而增大。对于相同θ值,当α从0.3增大到0.9时,vt分布曲线几乎无变化。
图8为vt,max的无量纲径向位置βmax沿α变化曲线,看到在整个发动机内,βmax几乎保持恒定,以上两方面共同说明,vt轴向衰减率非常小。
图9为轴向速度va分布曲线,α分别为0.3、0.6、0.9,轴向速度va曲线与0 m/s曲线交点的径向位置,即为涡幔(Mantle)[1]半径rm(无量纲涡幔半径βm定义为rm/R,如图9中所示)。相同α处,va随θ增大而增大,这是由于来流总动量中轴向动量所占比例增大导致的,与图7结果相一致。当α从0.9减小到0.3时,va曲线同样减小,说明va沿轴向具有显著衰减变化。
图10为入射倾角θ下βm的轴向分布,从入射口附近(α=1.2)到发动机顶端(α=0.2),βm以线性规律减小,线性斜率约为0.093 7。βm从α=1.2处的0.81±0.01减小至α=0.2处的0.73±0.01,该变化范围与文献[4,6,10]所得结果相一致。
3.2 入射压降Δpin对内流场涡结构影响
入射压降Δpin研究中,模型长径比αL=1.0,即发动机长度L=100 mm,入射压降分别为Δpin-1=41 700 Pa和Δpin-2=62 550 Pa,入射倾角θ分别为0°、10°、20°、30°。图11为α=0.6处无量纲压力Δp/Δpin径向分布。可看到,在0.19<β<1范围内,各曲线基本重合,在0<β<0.19范围内,压力曲线出现差异,Δpin-2压力曲线在β≈0.19变陡,斜率增大。图12为θ=0°、10°、20°、30°时,不同Δpin下,α=0.6处vt分布。可看到,从θ=0°增大到30°时,vt均随Δpin增大而增大,vt,max随θ增大而减小,这与3.1节中结论相一致。比较图11、图12可发现,压力曲线斜率增大位置与vt,max位置均出现在β≈0.19,这是由涡流理论决定的。对于涡流,存在式(1)所示力学平衡关系[18-19]:
(1)
以模型半径R对式(1)进行无量纲化,并进行变形,可得:
(2)
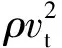
3.3 长径比αL对内流场涡结构影响
本节讨论中,对表1中所有工况进行了汇总。图13为Δpin=41 700 Pa所得结果,图14为Δpin=62 550 Pa所得结果。当Δpin=41 700 Pa时,各入射倾角下,不同αL所得βm的轴向分布并不相同。αL=1.0所得βm在整个发动机内均大于αL=1.5时,但二者变化趋势基本相同,均从入射口处附近(α=0.2)至发动机顶端处附近(对于αL=1.0,发动机顶端处附近α=0.8;对于αL=1.5,发动机顶端处附近α=1.2)以线性规律减小,且线性斜率近似相同。
对于vt,max,从图13(b)看到,各入射倾角下,不同αL所得βmax在整个发动机内均保持在0.19附近,αL对βmax几乎无影响。图13(c)为各入射倾角下,不同αL所得vt,max轴向分布。可看到,αL=1.0所得vt,max在整个发动机内均大于αL=1.5,且当αL=1.0时,vt,max在发动机内从入射口处附近至发动机顶端处附近逐渐减小。当αL=1.5时,vt,max在发动机内从入射口处附近至发动机顶端处附近,呈现出先增大、后减小的变化趋势。但对于αL=1.0和αL=1.5而言,vt,max变化范围均在3%以内。可知,vt,max的轴向衰减率非常小,与3.1节所得结论一致。
Δpin=62 550 Pa时,从图14(a)可知,βm轴向分布与Δpin=41 770 Pa相似,即αL=1.0所得βm在整个发动机内均大于αL=1.5时,且二者线性变化斜率也基本相同,βm变化范围为0.71±0.01~0.82±0.01。从图14(b)可知,βmax轴向分布也与Δpin=41 770 Pa时相似。从图14(c)可知,对于αL=1.0和αL=1.5两种工况,当θ相同时,αL=1.0所得vt,max与αL=1.5所得vt,max在数值上的差值明显要大于Δpin=41 770 Pa时,说明随着Δpin的增大,长径比αL对于vt,max大小的影响将增大。
4 结论
(1)切向速度vt及vt,max均随θ增大而减小,随Δpin增大而增大,随αL增大而减小。不同θ、不同Δpin、不同αL下,整个发动机内vt,max的径向位置βmax均恒定在0.19附近。αL=1.0时,vt,max从发动机顶端到入射口附近逐渐增大;αL=1.5时,vt,max从发动机顶端到入射口附近先增大、后减小。vt及vt,max的轴向衰减率非常小,维持在3%以内。
(2)轴向速度va随θ增大而增大,涡幔半径βm从发动机顶端开始线性增大到入射口附近,变化范围为0.71<βm<0.82,不同αL下,该线性斜率近似相同,va轴向衰减率要显著大于vt及vt,max。
(3)发动机内双向涡力学特性符合涡流理论,增大Δpin在增大vt及vt,max的同时,会使压力曲线在βmax附近梯度值增大。
(4)入射倾角θ相同时,随入射压降Δpin的增大,长径比αL对vt,max的影响将随之增强。
[1] Vyas A B,Majdalani J,Chiaverini M J.The bidirectional vortex part 1 an exact inviscid solution[C]//39th AIAA/ASME/SAE/ASEE Joint Propulsion Conference and Exhibit 20-23 July 2003,Huntsville,Alabama.
[2] Vyas A B,Majdalani J,Chiaverini M J.The bidirectional vortex part 2 viscous core corrections[C]//39th AIAA/ASME/SAE/ASEE Joint Propulsion Conference and Exhibit,20-23 July 2003,Huntsville,Alabama.
[3] Maicke B A,Majdalani J.Heuristic representation of the swirl velocity in the core of the bidirectional vortex[C]//37th AIAA Fluid Dynamics Conference and Exhibit,25-28 June 2007,Miami,FL.
[4] Chiaverini M J,Malecki M J,Majdalani J,et al.Vortex thrust chamber testing and analysis for O2-H2propulsion applications[C]//39th AIAA/ASME/SAE/ASEE Joint Propulsion Conference and Exhibit,20-23 July 2003,Huntsville,Alabama.
[5] 孙得川,白荣博,刘上.涡流冷壁推力室传热模型分析计算[J].计算机仿真,2011,28(4): 87-90.
[6] 孙得川,白荣博,刘上.涡流燃烧发动机燃烧室数值模拟[J].弹箭与制导学报,2011,31(2): 111-116.
[7] Sun De-chuan,Liu Shang.Experimental research on bidirectional vortices in cold wall rocket thruster[J].Aerospace Science and Technology,2011,18(2012): 56-62.
[8] 吴东波,李家文,常克宇.GH2/GO2涡流冷却推力室设计与数值计算[J].火箭推进,2010,36(5): 17-22.
[9] 李家文,唐飞,俞南嘉.推力室涡流冷却技术试验研究[J].推进技术,2012,33(6): 956-960.
[10] 唐飞,李家文,常克宇.涡流冷却推力室中涡流结构的分析与优化[J].推进技术,2010,31(2): 165-169.
[11] 李恭楠,俞南嘉,路强.涡流冷却推力室流场特征与性能仿真[J].航空动力学报,2014,29(2): 420-426.
[12] Fang D,Majdalani J,Chiaverini M J.Simulation of the cold-wall swirl driven combustion chamber[C]//39th AIAA/ASME/SAE/ASEE Joint Propulsion Conference and Exhibit,20-23 July 2003,Huntsville,Alabama.
[13] Maicke B A,Majdalani J.A constant shear stress core flow model of the bidirectional vortex[J].Proceedings of Royal Society Association,2009,465(3): 915-935.
[14] Maicke B A,Majdalani J.The compressible cidirectional vortex[C]//44th AIAA/ASME /SAE/ASEE Joint Propulsion Conference & Exhibit,21-23 July 2008,Hartford,CT.
[15] Saad T,Majdalani J.Energy based solutions of the bidirectional vortex[C]//44th AIAA/ASME /SAE/ASEE Joint Propulsion Conference & Exhibit,21-23 July 2008,Hartford,CT.
[16] Maicke B A,Majdalani J.On the compressible bidirectional vortex part 1 a bragg-hawthorne stream function formulation[C]//50th AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition,09-12 January 2012,Nashville,Tennessee.
[17] Maicke B A,Majdalani J.On the compressible bidirectional vortex part 2 a beltramian flowfield approximation[C]//50th AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition,09-12 January 2012,Nashville,Tennessee.
[18] Basina I P,Tonkonogii A V,Kukueev B N.Motion of burning particles in cyclone chambers[J].Thermal Engineering,1974,21(3): 99-103.
[19] Georgios H V.Tangential velocity and static pressure distributions in vortex chambers[J].AIAA Journal,1987,25(8): 1139-1140.
(编辑:崔贤彬)
Numerical research of compressible vortex combustion cold-wall chamber
DANG Jin-feng,GAO Ye,LIU Ping-an
(College of Aerospace and Civil Engineering,Harbin Engineering University,Harbin 150001,China)
In order to deeply investigate the inner relationship between the inlet parameters and the structure characteristics of bidirectional vortex in the Vortex Combustion Cold-Wall Chamber(VCCWC),the compressible cold simulation research of the VCCWC was carried out based on three-dimensional physical model.The inlet parameters included injection angle,injection pressure drop and chamber length.Three models,including RSM model,RNGk-εmodel with swirl factor and RNGk-εmodel,were compared with the experimental data in the pre-research.The RNGk-εmodel with swirl factor was finally selected as the numerical turbulent model based on the performance of the accuracy and the cost.Results show that: the tangential velocity and the maximum tangential velocity decrease with the injection angle and length to diameter ration but increase with the injection pressure drop.The dimensionless radial positon of the maximum tangential velocity is kept around 0.19 in the whole chamber regardless of injection angle,injection pressure drop and the length to diameter ratio.For the different length to diameter ratio,the maximum tangential velocity increases for the length to diameter ratio of 1.0 but increases first and then decreases for the length to diameter ratio of 1.5 from the top of the chamber to the injection section.The axial decay rates of the tangential velocity and the maximum tangential velocity are kept within 3%.The dimensionless mantle radius is not kept constant but linearly increases from the top of the chamber to the injection section.The range of the dimensionless mantle radius is from 0.71 corresponding to 0.82.For the same injection angle,the impact of the length to diameter ratio to the magnitude of the maximum tangential velocity will strengthen with the increase of the injection pressure drop.
vortex combustion cold-wall chamber;compressible;turbulent models;injection conditions;length to diameter ratio;simulation
2015-09-06;
2015-12-21。
自然科学基金面上项目(11372079);中央高校基本科研基金(HEUCFD1404)。
党进锋(1987—),男,博士生,研究方向为涡流旋转燃烧发动机数值研究。E-mail:dangjinfeng1987@163.com
V434.13
A
1006-2793(2017)01-0016-08
10.7673/j.issn.1006-2793.2017.01.003

