永磁同步电机滑模变结构MRAS转速辨识

尚飞，霍海波

（三门峡职业技术学院电气工程学院，河南 三门峡 472000）

永磁同步电机滑模变结构MRAS转速辨识

尚飞，霍海波

（三门峡职业技术学院电气工程学院，河南 三门峡 472000）

结合模型参考自适应方法和滑模变结构方法的各自优点，提出了一种新型永磁同步电机速度估计器。首先给出了永磁同步电机的数学模型，并在此基础上设计了积分反步控制与滑模变结构模型参考自适应系统相结合的无速度传感器矢量控制系统。积分反步控制法和滑模变结构模型参考自适应分别实现了给定速度、电流的无静差跟踪以及对实际速度的快速准确跟踪。利用Lyapunov函数证明了所设计的控制器的稳定性。最后仿真结果表明所提出的方法能够实现速度的快速精确跟踪控制。

永磁同步电机；无速度传感器控制；滑模变结构；模型参考自适应系统

永磁同步电机因其具有结构简单、可靠性高、体积小等优点，在航天以及高精度数控机床中得到了广泛应用［1-2］。由于永磁同步电机是一个非线性、多变量强耦合系统，受电机参数多变、外部负载扰动等因素的影响，传统的PI控制方法并不能满足永磁同步电机高性能、高精度的控制要求［3-5］。

目前，很多智能的控制方法在永磁同步电机中得到了成功的应用，如自适应控制策略［6］、神经网络控制法［7］、模糊控制法［8］等。其中自适应控制策略虽然大大降低了电机参数以及外部负载扰动对永磁同步电机控制性能的影响，但该控制方法中参数的设计大大增加了控制器复杂性；模糊控制智能性较强，但模糊控制规则表的设计较复杂；神经网络控制方法需要进行网络训练优化和选取最佳初始值，计算复杂使其应用具有一定的局限性。反步控制是最近针对非线性系统发展而来的一种智能控制策略，主要是将非线性系统进行分解，得到阶次低于系统阶次的子系统，并不断从后推导得到整个系统，从而完成整个控制器的设计［9-11］。

永磁同步电机在位置跟踪和速度跟踪控制过程中，可以通过安装位置或者速度传感器进行跟踪控制，但由于传感器的安装相应地增加了产品的成本，此外增加了电机转轴的转动惯量，对子系统的动静态性能造成了不利影响。针对此情况可以利用电机绕组中的一些信号，通过计算估计电机转子的位置以及速度从而实现电机位置和速度的跟踪。文献［12］提出了通过采集感应电动势，实现了电机转速和位置的估计，该方法在低速情况下估计效果并不理想；文献［13］提出了一种状态观测器的估计方法，但该方法计算量较大，参数具有不确定性。文献［14］提出了一种高频信号注入方法实现估计，该控制方法避免了坐标变换，避免了转子估计误差的影响，但此控制策略容易影响电机的动态性能，此外需要外部设备进行信号的注入，相应增加了成本。

模型参考自适应（MRAS）具有结构简单、计算复杂度低，因其具有优良的转速和位置估计性能，从而被广泛关注。而滑模变结构控制法能够很好地抑制电机参数多变、负载扰动等因素对电机控制性能的影响，并具有快速的动态响应特点，因此本文利用模型参考自适应和滑模变结构的优点设计了一种新型永磁同步电机的速度估计器，并利用Lyapunov函数证明了系统的稳定性。最后通过仿真分析证明了该方法的有效性。

1 PMSM数学模型

在d-q坐标系下的PMSM的定子电压方程为

式中：id为定子电流d轴分量；iq为定子电流q轴分量；ud为定子电压d轴分量；uq为定子电压q轴分量；Rs为定子电阻；对于面贴式PMSM，L为定子电感，Ld=Lq=L；pn为磁极对数；Ψf为转子的磁链；ωr为角速度；p为微分算子，

机械运动方程为

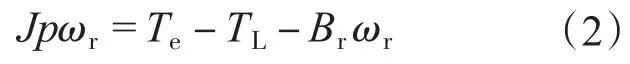
式中：Te为电磁转矩；TL为负载转矩；Br为阻力摩擦系数；J为转动惯量。

2 PMSM无速度传感器矢量控制系统设计

2.1 滑模变结构模型参考自适应速度估计

以永磁同步电机在d-q坐标系上d,q轴上的电流id,iq为观测量，由式（1）可得速度估计的模型参考自适应系统的参考模型为

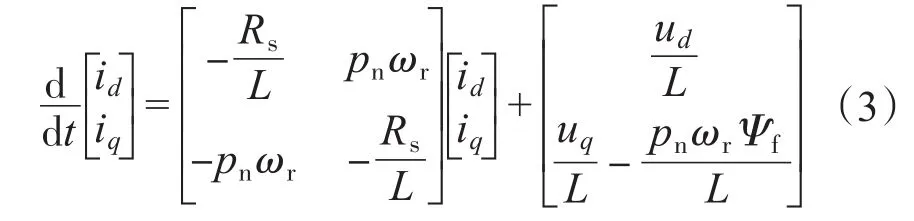
由于速度是不可知的，由式（1）可得到速度估计的参考自适应系统的可调模型为

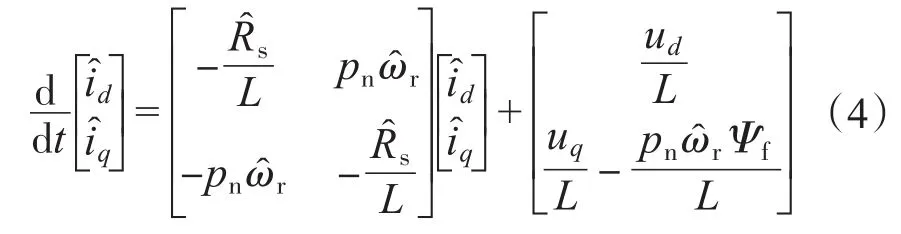
由式（3）和（4）可得：

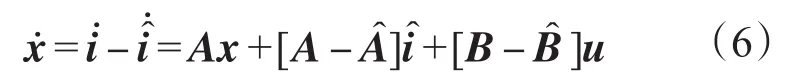
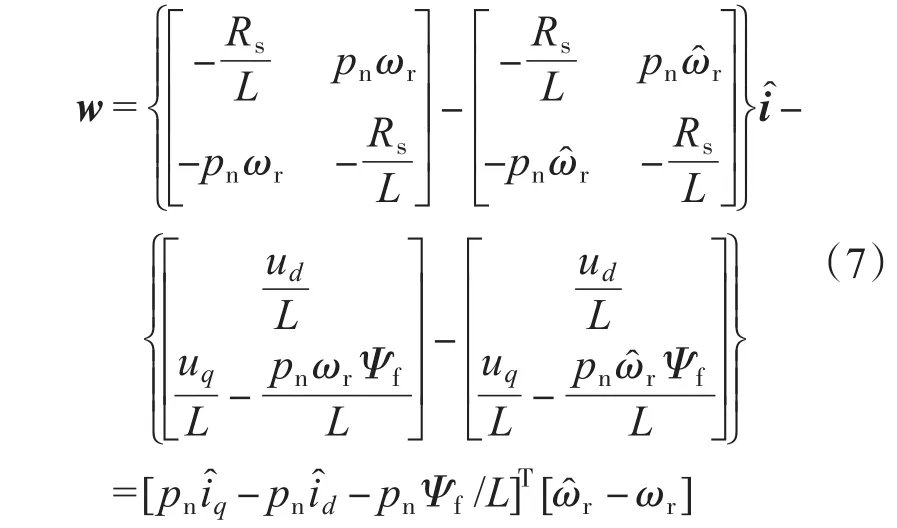
假设广义误差方程为v=Cx，则线性状态方程为

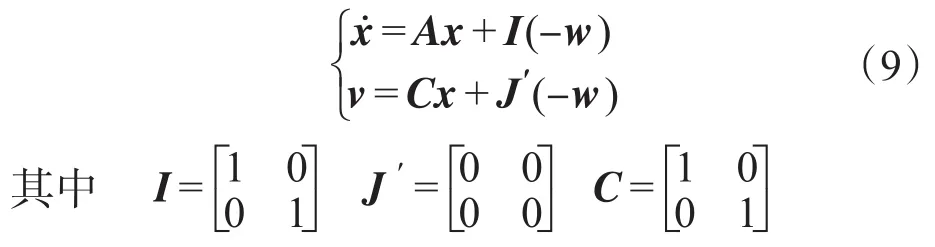
由式（8）和式（9）可得：

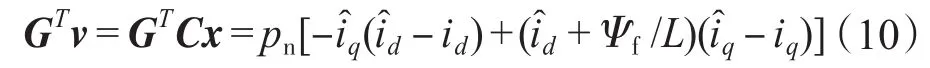
定义：

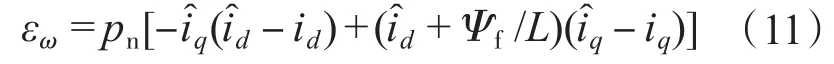
因此可以得到传统模型参考自适应方法速度估计的自适应律为

式中：Kp为比例增益；Ki为积分增益；p为微分算子。

传统的PI控制方法由于参数是固定的，当速度估计器因扰动受到影响时，不能得到最佳的控制性能。本文提出了一种新型的变结构方法的自适应律以代替传统的PI控制在模型参考自适应速度估计器中。

在此选择的速度估计器的滑模面为

式中：k为正常数。

设计基于变结构模型参考适应的速度估计器为

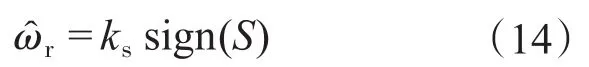
式中：ks为滑模增益，S为设计的积分滑模面。进一步求解可得：

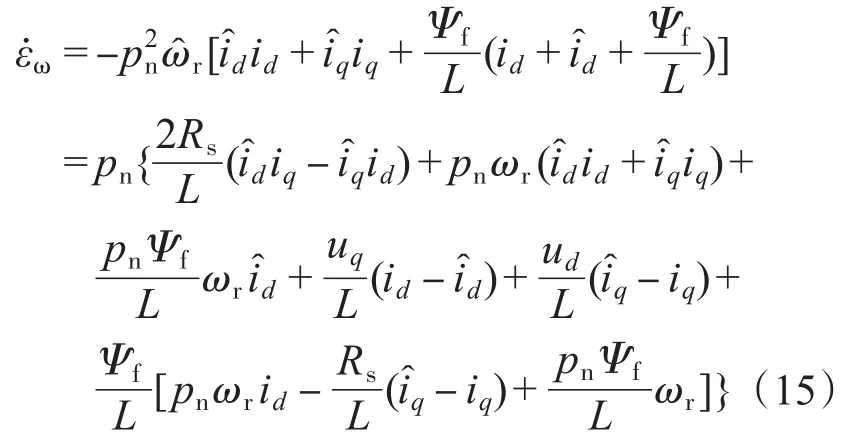
定义f1，f2为

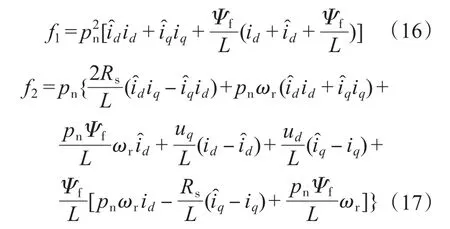
则由式（15）可得：

为了说明所设计的速度估计器的稳定性，选择Lyapunov函数为

对式（19）求导可得：

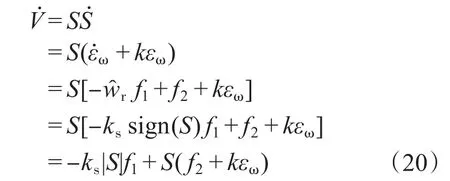
由于f1≥0，，因此存在1个较大的正数ks，使得，从而保证本文所设计控制器趋于稳定。

2.2 积分反步速度控制

假设速度跟踪误差为

设iq为虚拟控制量，设计带有速度控制误差积分作用的Lyapunov函数为

其中

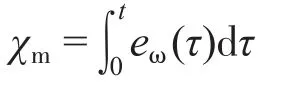
式中：K0为正常数。

对式（22）求导可得：

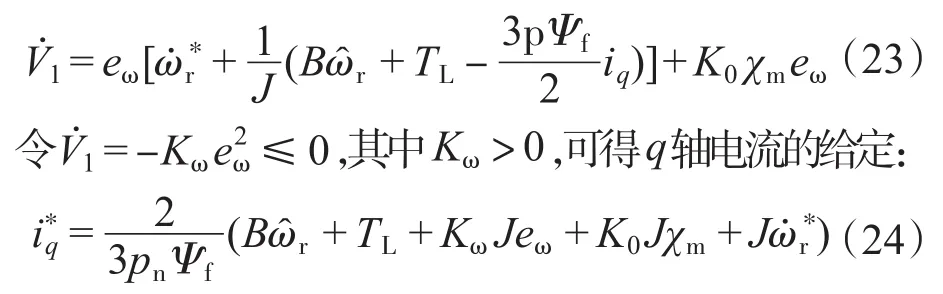
定义d-q轴电流跟踪误差为并求导可得：

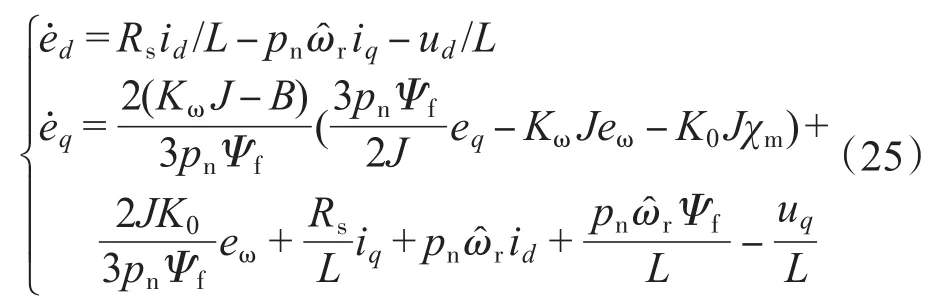
假设控制系统Lyapunov函数为

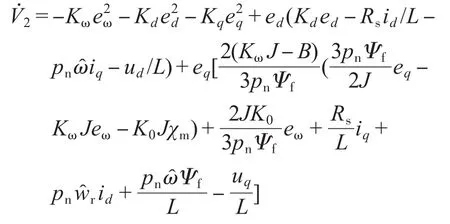
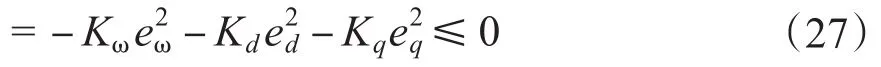
由式（27）可得控制电压ud,uq为

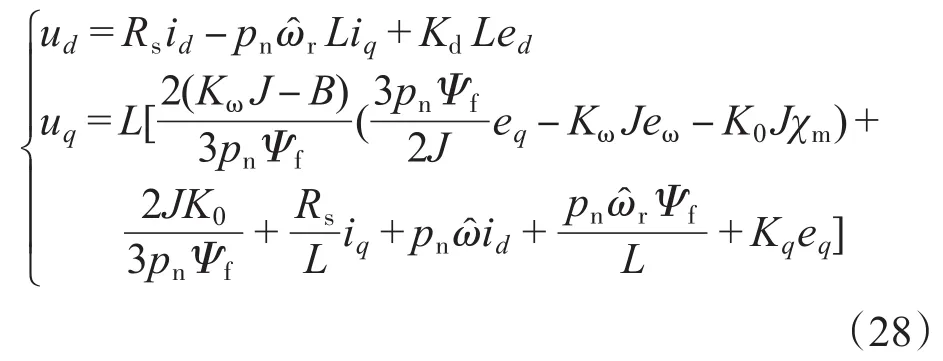
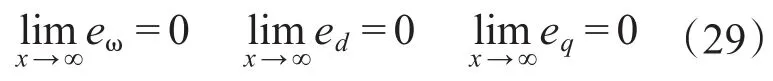
3 仿真与实验

为了验证本文所提出的反步滑模控制策略的正确性与有效性，对PI控制与基于积分反步滑模控制方法分别进行了仿真与实验对比研究。电机参数为：额定转速2 000 r/min，额定转矩8 N·m，定子电阻0.958 6 Ω，d轴和q轴电感0.005 26 H，磁极对数4，转子磁链0.182 6 Wb，转动惯量0.000 632 8 kg·m2，摩擦系数0.000 303 6 N·m·s，图1为设计的控制系统框图。

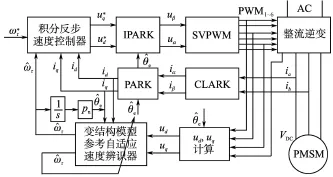
图1 永磁同步电机控制系统结构Fig.1 Control system structure of PMSM

在Matlab/Simulink软件环境中分别对基于PI控制方法的永磁同步电机控制系统与基于积分反步滑模控制方法的永磁同步电机调速系统进行了仿真分析。

仿真结果如图2和图3所示。图2为传统PI控制时PMSM调速系统仿真结果，在0.1 s时负载转矩从0 N·m突然增加到4 N·m，在0.2 s时负载转矩从4 N·m又变为0 N·m；图3为基于积分反步滑模的PMSM调速系统仿真结果，同样在0.1 s时负载转矩从0 N·m突然增加到4 N·m，在0.2 s时负载转矩从4 N·m又变为0 N·m。

图2 PI控制策略下系统仿真Fig.2 System simulation under PI control strategy

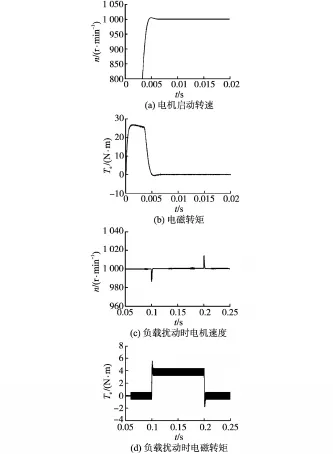
图3 积分反步滑模控制策略下系统仿真Fig.3 System simulation of integral backstepping sliding mode control strategy

由图2和图3仿真结果可以看出，相对PI控制方法，当PMSM启动参考转速为1 000 r/min时，基于积分反步滑模控制策略下，永磁同步电机启动转速具有很小的超调量和上升时间；而当负载转矩突然变大或者突然变小时，在积分反步滑模控制方法下的永磁同步电机转速以及转矩响应波动相比PI控制时均较小。

为了进一步验证本文所提方法的有效性，构建了永磁同步电机速度控制实验平台并进行了相关的实验。整个电机控制系统中采集到的数据先经过A/D转换后再用示波器显示并保存，实验波形如图4和图5所示。

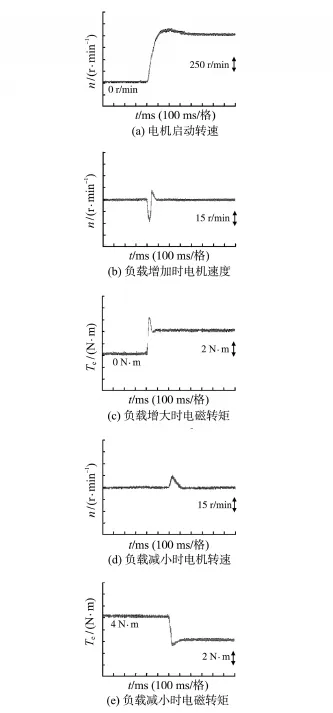
图4 PI控制下的系统实验结果Fig.4 System experimental results under PI control

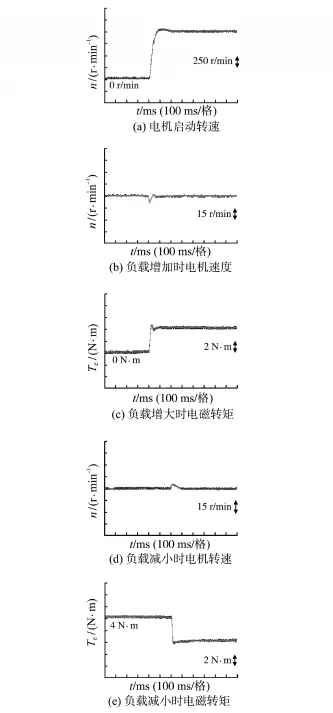
图5 积分反步滑模控制下系统实验结果Fig.5 Experimental results of the system with integral backstepping sliding mode control

图4为PI控制方法实验结果，图5为基于积分反步滑模控制时的实验结果。图4a与图5a为电机启动参考转速为1 000 r/min时，以上2种控制方法的PMSM启动转速波形结果，在电机转速稳定在1 000 r/min后进行了负载实验；图4b、图4c与图5b、图5c分别为2种不同控制方法下负载突然增加时电机转速以及电磁转矩的动态响应；图4d、图4e与图5d、图5e为负载突然卸载时2种不同控制方法下的转速与电磁转矩的动态响应曲线。

图6为积分反步滑模控制时对扰动进行估算的实验波形。

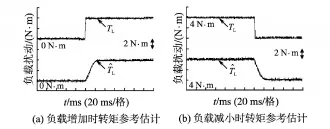
图6 积分反步滑模控制时负载扰动估计Fig.6 Load disturbance estimation for integral backstepping sliding mode contro

图7为电机转速由500r/min增加到1000r/min时，实际转速和估计转速的实验波形。

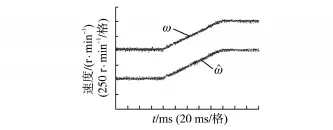
图7 实际转速与估计转速Fig.7 Actual speed and estimated speed

由实验结果可以看出，本文所提控制方法能够快速准确地对负载扰动进行估计，且估计结果平滑基本没有抖振；而传统PI控制当负载变化时，电机转速和电磁转矩均出现了较大程度的波动。积分反步滑模控制与PI控制相比，电机转速以及电磁波动均较小，在扰动变化时，能够保证系统稳态性能，因此本文所提控制方法对系统扰动能够有效抑制，提高了系统抗扰动能力。

4 结论

本文设计了一种基于积分反步控制的PMSM滑模变结构模型参考自适应的无速度传感器的调速系统。首先给出了永磁同步电机的数学模型，并在此基础上设计了积分反步控制和滑模变结构模型参考自适应系统相结合的无速度传感器矢量控制系统。积分反步控制法和滑模变结构模型参考自适应分别实现了给定速度、电流的无静差跟踪以及对实际速度的快速准确跟踪。利用Lyapunov函数证明了本文所设计的控制器的稳定性。仿真结果表明本文所设计的方法能够实现给定速度的快速跟踪控制，具有很强抗扰动特性。

［1］张月玲，党选举.基于死区迟滞函数的永磁同步直线电机滑模控制［J］.中国电机工程学报，2011，31（3）：67-74.

［2］Andon V T，Giuseppe L C，Vincenzo G，et al.Sliding Mode Neuro-adaptive Control of Electronic Drives［J］.IEEE Trans⁃actions on Industrial Electronics，2007，54（1）：671-679.

［3］Rachid E，Mohand O.Nonlinear Predictive Controller for a Permanent Synchronous Motor Drive［J］.Mathematics and Computer in Simulatin，2010，81（2）：394-406.

［4］Mohamed Y A R I，EI-Saadany E F.A Current Control Scheme with an Adaptive Internal Model for Torque Ripple Minimization and Robust Xurrent Regulation in PMSM Drive Systems［J］.IEEE Transactions on Energy Conversion，2008，23（1）：92-100.

［5］Chang S H，Chen P Y，Ting Y H，et al.Robust Current Con⁃trol-based Sliding Mode Control with Simple Uncertainties Es⁃timation in Permanent Magnet Synchronous Motor Drive Sys⁃tems［J］.Electric Power Application，IET.2010，4（6）：441-450.

［6］CHOI H H，VU N T T，JUNG J W.Digital Implementation of an Adaptive Speed Regulator for a PMSM［J］.IEEE Transac⁃tions on Power Electronics，2011，26（1）：3-8.

［7］WANG J，WANG H H，ZHANG X Q，et al.Neural Network Vector Control of a Permanent Magnet Synchronous Motor Drive［C］//The 3rdIEEE Conference on Industrial Electronics and Applications.New York：IEEE，2008：542-546.

［8］王艳敏，冯勇，陆启良.永磁同步电动机的无抖振滑模控制系统设计［J］.电机与控制学报，2008，12（5）：514-520.

［9］张晓光，赵克，孙力，等.永磁同步电动机滑模变结构调速系统新型趋近率控制［J］.中国电机工程学报，2011，31（24）：77-82.

［10］Bai K I C，Kim K H，Youn M J.Robust Nolinear Speed Con⁃trol of PM Synchronous motor Using Boundary Layer Integral Sliding mode Control Technique［J］.IEEE Transactions on Control Systems Technology，2000，8（1）：47-54.

［11］汪海波，周波，方斯琛.永磁同步电机调速系统的滑模控制［J］.电工技术学报，2009，24（9）：71-77．

［12］CHEN Z Q，TOMITA M，DOKI S，et al.An Extended Electro⁃motive Force Model for Sensorless Control of Interior Perma⁃nent-magnet Synchronous Motors［J］.IEEE Transactions on Industrial Electronics，2003，50（2）：288-295.

［13］陆华才，徐月同.基于AEKF的永磁直线同步电机速度和位置估计算法［J］.中国电机工程学报，2009，29（33）：90-94.

［14］REIGOSA D D，GARCIA P，BRIZ F，et al.Modeling and Adaptive Decoupling of High-frequency Resistance and Tem⁃perature Effects in Carrier-based Sensorless Control of PM⁃Synchronous Machines［J］.IEEE Transactions on Industry Applications，2010，46（1）：139-149.

Sliding Mode Variable Structure MRAS Speed Estimator for Permanent Magnet Synchronous Motors

SHANG Fei，HUO Haibo
（Electrical Engineering College，Sanmenxia Vocational and Technical College，Sanmenxia 472000，Henan，China）

Based on the advantages of the model reference adaptive method and the sliding mode variable structure method，a new type of permanent magnet synchronous motor speed estimation was proposed.Firstly，the mathematical model of the permanent magnet synchronous motor was presented，and then the non speed sensor vector control system based on the backstepping controller with integral action and sliding mode variable structure model reference adaptive system was designed.The backstepping controller with integral action method and the sliding mode variable structure model reference adaptive system were used to realize the given speed，the non static error tracking of the current，the fast and accurate tracking of the actual speed.The stability of the controller designed was proved by using the Lyapunov function.Finally，the simulation results show that the proposed method can achieve fast and accurate tracking control.

permanent magnet synchronous motor；sensorless control；sliding mode variable structure；model reference adaptive system

TP271.4

A

10.19457/j.1001-2095.20170202

2016-01-26

修改稿日期：2016-06-15

尚飞（1979-）男，硕士，讲师，Email：sfhnsmx@sina.com