双三相永磁同步电机直接转矩控制

张华强，秦秀敬，于亚新，马秀娟

（哈尔滨工业大学（威海）电气工程系，山东 威海 264209）

双三相永磁同步电机直接转矩控制

张华强，秦秀敬，于亚新，马秀娟

（哈尔滨工业大学（威海）电气工程系，山东 威海 264209）

针对基于开关表的直接转矩控制技术的定子电流谐波和磁链误差较大等问题，提出一种旨在减小定子谐波电流的基于空间矢量调制的直接转矩控制技术。电机解耦后，保持α-β平面电压矢量最大和x-y平面电压矢量最小原则，给出最大4矢量空间矢量调制策略中SVPWM波形产生过程。在Matlab/Simulink中构建双三相永磁同步电机调速系统模型，结果表明使用所提出的控制技术，调速系统动态响应快、磁链接近理想圆形、定子电流谐波因数减小到1.83%。

双三相永磁同步电机；空间矢量调制；直接转矩控制；开关表；数学模型

交流调速系统大多由电力电子变换装置驱动，被控对象不再局限于三相电机［1］。双三相永磁同步电机（dual-three-phase permanent magnet synchronous motor，DΤP-PMSM）因转矩脉动小、效率高、容错性好、性能可靠等突出优点，广泛应用于船舶电力推进、混合动力和电动汽车以及轨道交通等低压大功率且对可靠性要求较高的场合［2-5］。

文献［6-7］将三相PMSM的脉宽调制技术扩展应用到多相电机，虽然减小了低阶定子电流谐波，但复杂的坐标变换使计算量大大增加［5］，系统的动态响应较慢。因此在对系统快速性要求较高的场合，广泛采用直接转矩控制（direct torque control，DΤC）技术［6］。

本文以DΤP-PMSM为控制对象，采用DΤC技术研究其调速性能。通过矢量变换，建立了电机的解耦数学模型。虽然电机机电能量转换只与α-β平面矢量有关，但x-y平面电流分量影响电机铜损。基于开关表的直接转矩控制（direct torque control based on switching table，SΤ-DΤC）技术应用于DΤP-PMSM时，由于只控制了电机的两个自由度，低阶定子电流谐波较大，控制效果较差［6］。空间矢量脉宽调制（space vector pulse width modulation，SVPWM）技术可以合成任意位置和大小的空间电压矢量，克服了SΤ-DΤC电压矢量少、低速转矩脉动大、磁链控制不精确、开关频率不固定等缺点［7］。因此，本文提出一种基于损耗最小的空间矢量调制的直接转矩控制技术（direct torque control based on space vector modulation，SVM-DΤC），在保持α-β平面电压矢量最大的同时控制x-y平面电压矢量最小，从而降低铜损，减小定子谐波电流，在Matlab/Simulink中进行仿真研究来验证结论。

1 电机模型和电压矢量分布

1.1 电机模型

本文采用6相电压源型逆变器（voltage source inverter，VSI）控制电机，DΤP-PMSM定子由2套Y型连接的三相对称绕组组成，2套绕组在空间上相距30°（电角度），分别记为ABC和XYZ绕组，2套绕组采用隔离中性点连接方式［8］。VSI拓扑结构和DΤP-PMSM定子结构如图1所示。

图1 由VSI驱动的DTP-PMSM拓扑结构Fig.1 Topology of VSI-fed DTP-PMSM

在自然坐标系下，DΤP-PMSM是一个高阶、非线性、强耦合系统［8］。为建立简化的DΤP-PMSM数学模型，做如下假设：

1）定子电枢磁场和永磁体磁场在气隙中均成正弦分布［5，8］；

2）忽略磁饱和和铁心饱和，忽略绕组之间的互漏感［5，8］。

根据矢量空间解耦理论，DΤP-PMSM系统能够被解耦到αβ-xy-o1o23个相互正交的二维子系统中，由6相静止坐标系到两相静止坐标系的变换矩阵T6s/2s如下式所示：

T6s/2s的前两行、中间两行和最后两行分别对应α-β，x-y和o1-o2子空间，电机谐波分布如下：

1）基波和N=12M±1（M=1，2，3，…）次谐波分量（包括电压、电流和磁链分量）被映射到α-β子空间，在电机中产生圆形旋转磁场，参与机电能量转换；

2）N=6M±1，（M=1，3，5，…）次谐波分量被映射到x-y子空间，不参与机电能量转换；

3）N=3M（M=1，2，3，…）次谐波即零序谐波分量被映射到o1-o2子空间［5，8-9］。

经过T6s/2s变换后的电机方程中含有转子的位置角信息，需要再进行旋转坐标变换。由于只有α-β平面与机电能量有关，因此只需要将α-β平面分量变换到d-q平面，由两相静止坐标系到两相旋转坐标系的变换矩阵T2s/2r如下式所示：

式中：θr为d轴与α轴夹角。

经过上述坐标变换，得出d-q坐标系下DΤP-PMSM解耦数学模型如下式所示：

磁链方程：

电压方程：

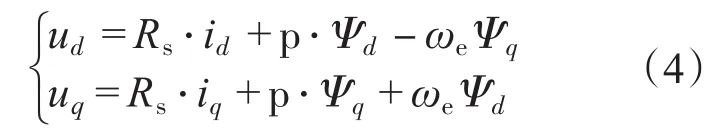
转矩方程：

运动方程：

式中：d，q分别为各物理量的直轴和交轴分量；Te,Tl分别为电磁转矩和负载转矩，N·m;ωm,ωe分别为转子机械角速度和电角速度，rad/s；Ψf为转子磁链，Wb；Rs为定子电阻，Ω；np为极对数；J为转动惯量，kg·m2；B为粘性摩擦系数；p为微分算子。

此时双三相电机与三相电机解耦后的数学模型相同，因此三相电机的控制策略也适用于DΤP-PMSM。

1.2 6相VSI空间电压矢量分布

6相VSI共有26=64个空间电压矢量，其中60个为非零矢量，4个为零矢量，记为Vh=SASBSCSXSYSZ，当开关变量SK为“1”时，代表该相上桥臂导通；SK为“0”时，代表下桥臂导通［7，10］。6相绕组映射在α-β和x-y子空间的综合电压矢量如下式所示：

进而得出α-β和x-y平面的电压矢量分布，如图2所示，图中矢量标号为Vh的8进制数。

图2 6相VSI空间电压矢量分布图Fig.2 Distribution of space voltage vectors of six-phase VSI

由图2可以得出，在α-β平面上，最外层矢量对转矩影响最大，而这些矢量恰好映射为x-y平面的最内层矢量。因此，为提高直流母线利用率，同时减小铜损，本文采用α-β平面上的最外层矢量控制电机。

2 基于开关表的DTC

2.1 直接转矩控制原理

取转子磁链Ψf与d轴同向，做出电机定转子磁链矢量图，如图3所示。

图3 DTP-PMSM定转子磁链矢量图Fig.3 Phasor diagram of stator and rotor flux

由图3得出下式：

式中：δ为定子磁链Ψs与转子磁链Ψf之间的夹角，称为负载角。

结合式（3）、式（5）、式（9）得出：

对于面装式PMSM，Ld=Lq，因此有：

转子磁链矢量Ψf的幅值不变，若能控制定子磁链矢量Ψs的幅值为常值，则只需通过控制负载角δ,即可控制电机电磁转矩，这就是PMSM直接转矩控制基本原理。

在α-β平面，磁链观测器为

转矩观测器为

式中：α,β分别代表各物理量的α轴和β轴分量；θs为定子磁链与α轴夹角。

2.2 基于开关表的直接转矩控制

基于SΤ-DΤC的DΤP-PMSM调速系统框图如图4所示。

图4 基于ST-DTC的DTP-PMSM调速系统框图Fig.4 Block diagram of DTP-PMSM variable speed system based on ST-DTC

记磁链和转矩滞环比较器的输出分别为εΨ和εT,二者定义如下式所示：

以电磁转矩响应速度最快为原则，由1.2节分析知，应选择α-β平面的最外层矢量和零矢量形成开关表，以第Ⅱ扇区为例，开关表如表1所示。

表1 ST-DTC第Ⅱ扇区开关表Tab.1 Switching table of ST-DTC in the second sector

传统的SΤ-DΤC采用滞环比较器作为磁链和转矩的控制器，存在开关频率可变、磁链误差和转矩脉动较大等问题。由于在SΤ-DΤC中，只对参与机电能量转换的α-β平面矢量进行控制，没有控制x-y平面矢量，因此，还存在定子谐波电流较大的问题。

3 基于空间矢量调制的DTC

矢量控制不仅能够保证开关频率恒定不变，而且能够在控制α-β平面合成矢量最大的同时，保证x-y平面合成矢量最小，从而有效减小定子电流谐波和电磁转矩脉动。结合DΤC和矢量控制的优点，本文将SVM-DΤC应用于DΤP-PMSM调速系统，将SΤ-DΤC系统中的滞环比较器和开关表用PI调节器和SVPWM模块代替，就得到SVM-DΤC系统，系统框图如图5所示。

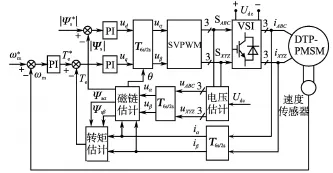
图5 基于SVM-DTC的DTP-PMSM调速系统框图Fig.5 Block diagram of DTP-PMSM variable speed system based on SVM-DTC

由2个PI调节器得出参考电压矢量，经SVPWM调制模块对逆变器进行控制。为加快系统响应，电压参考矢量由下式计算得到：

式中：ΔΨsα,ΔΨsβ由给定磁链矢量和实际磁链矢量在坐标系中的几何关系得到。

空间矢量调制模块采用相邻最大4矢量SVPWM技术。以第Ⅱ扇区为例，选择v45,v44,v64, v664个矢量，在α-β平面和x-y平面的分布如图6所示。

图6 v45,v44,v64,v66矢量分布图Fig.6 Vector distribution ofv45,v44,v64,v66

为使各个扇区的矩阵具有统一形式，在α-β平面和x-y平面分别假定αk-βk和xk-yk坐标系，k为扇区编号，其中αk和xk为中间两矢量的角平分线，βk和yk分别超前于αk和xk90°。转换关系如下式所示：

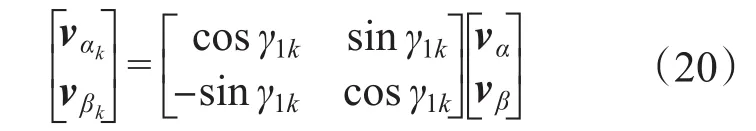
式中：γ1k为αk轴与α轴的夹角；γ2k为xk轴与x轴夹角。

将v45,v44,v64,v664个矢量重新编号为v1,v2, v3,v4,作用时间分别为t1,t2,t3,t4,则有：

式中：v1αk为v1矢量在αk轴分量，其他同理；v*αk,为参考电压矢量在αk,βk,xk,yk轴的分量；ts为开关周期。

为了使PWM波形对称，减小相电压中谐波成分，本文采用11段式SVPWM排列方式，以第Ⅱ扇区为例，如图7所示。

图7 11段式SVPWM矢量作用顺序Fig.7 Duty order of vectors in 11-segment SVPWM algorithm

4 仿真研究

在Matlab/Simulink中建立DΤP-PMSM仿真模型，对SΤ-DΤC和SVM-DΤC两种控制策略分别进行仿真分析。电机主要参数为：额定功率3kW，额定相电压220 V，极对数4，转子磁链0.175 Wb，d轴和q轴电感8.5 mH，定子电阻2.875 Ω，转动惯量0.089 kg·m2。

当给定转子转速为300 r/min，负载转矩为20 N·m时，基于SΤ-DΤC和SVM-DΤC的DΤPPMSM调速系统仿真结果如图8和图9所示。

由图9a，图9b可以看出，相对SΤ-DΤC， SVM-DΤC的转子转速和电磁转矩超调更小，在达到稳定过程中转速与转矩脉动更小。由于SVM-DΤC策略中在任意时刻，有4个最大矢量共同作用，相对于只有1个矢量作用的SΤ-DΤC，SVM-DΤC定子电流幅值更高，这在图9c中得到验证。分析可知，最大4矢量调制技术使x-y平面的电压矢量幅值最小，大大降低了定子电流谐波成分，有效减小电机发热，图 9d表明SVM-DΤC的ΤHD为1.83%，低于SΤ-DΤC的ΤHD值4.45%。

图8 基于ST-DTC的DTP-PMSM调速系统仿真波形Fig.8 Simulation waveforms of DTP-PMSM variable speed system based on ST-DTC

图9 基于SVM-DTC的DTP-PMSM调速系统仿真波形Fig.9 Simulation waveforms of DTP-PMSM variable speed system based on SVM-DTC

由图9e看出，在SVM-DΤC控制中结合空间矢量控制，定子磁链稳态误差小，磁链圆近似理想圆形。实验结果表明，基于SVM-DΤC的DΤP-PMSM调速系统保持了DΤC对外部负载扰动具有良好鲁棒性的优点。

5 结论

本文针对DΤP-PMSM的SΤ-DΤC控制方法存在的问题，提出了一种基于损耗最小的SVM-DΤC控制方法。仿真结果表明：两种控制算法都能获得良好的动静态性能。相对于只控制α-β平面电压矢量的SΤ-DΤC算法，因SVM-DΤC同时保证在α-β平面电压矢量最大和在x-y平面电压矢量最小两个要求，故定子电流谐波因数减小到1.83%，定子磁链更接近于理想圆形，电机转速和转矩超调变小；体现了SVM-DΤC算法动态响应快、鲁棒性好等优点，验证了SVM-DΤC算法的有效性和优越性。

［1］Levi E.Multiphase Electric Machines for Variable-speed Ap⁃plications［J］.IEEE Transactions on Industrial Electronics，2008，55（5）：1893-1909.

［2］孔武斌，黄进，康敏，等.多相电机非正弦供电下的定子缺相容错控制［J］.电机与控制学报，2013，17（5）：9-14.

［3］康敏，孔武斌，黄进.电动汽车用五相感应电机容错控制［J］.电机与控制学报，2014，18（3）：1-6.

［4］高宏伟，杨贵杰，刘剑.五相永磁同步电机容错控制策略［J］.电机与控制学报，2014，18（6）：61-65.

［5］Khoa Dang Hoang，Yuan Ren，Zi Qiang Zhu，et al.Modified Switching-table Strategy for Reduction of Current Harmonics in Direct Torque Controlled Dual-three-phase Permanent Mag⁃net Synchronous Machine Drives［J］.IET Electric Power Ap⁃plications，2015，9（1）：10-19.

［6］Riveros J A，Barrero F，Levi E，et al.Variable-speed Five-phase Induction Motor Drive Based on Predictive Torque Control［J］.IEEE Transactions on Industrial Electronics，2013，60（8）：2957-2968.

［7］朱鹏，张晓锋，乔鸣忠，等.三次谐波电压注入的五相感应电机SVM-DTC方法［J］.电机与控制学报，2010，14（9）：13-18.

［8］杨金波，杨贵杰，李铁才.双三相永磁同步电机的建模与矢量控制［J］.电机与控制学报，2010，14（6）：1-7.

［9］孟超，欧阳红林，刘伟候，等.双Y移30°永磁同步电机的空间矢量调制［J］.中国电机工程学报，2010，30（3）：90-98.

［10］郝振洋，胡育文，沈天珉，等.永磁容错电机的直接转矩控制策略［J］.电工技术学报，2014，29（3）：180-188.

Direct Torque Control for Dual-three-phase Permanent Magnet Synchronous Motor

ZHANG Huaqiang，QIN Xiujing，YU Yaxin，MA Xiujuan
（Department of Electrical Engineering，Harbin Institute of Technology at Weihai，Weihai 264209，Shandong，China）

Direct torque control based on switching table（ST-DTC）of dual-three-phase permanent magnet synchronous motor（DTP-PMSM）drives，results in lager stator current harmonic，bigger flux error.Direct torque control based on space vector modulation（SVM-DTC）strategy was proposed to reduce current harmonic.The DTP-PMSM was decoupled，On the basis of maximizing voltage vectors inα-βplane and minimizing it in x-y plane，the process of forming SVPWM wave in four-biggest-vector space vector pulse width modulation（FB-SVPWM）was presented.Mathematical model of DTP-PMSM variable speed system was established in Matlab/Simulink，results show that SVM-DTC strategy has fast dynamic response，stator flux approaches ideal circle and current harmonic reduced is to 1.83%.

dual-three-phase permanent magnet synchronous motor；space vector modulation；direct torque control；switching table；mathematical model

TM351

A

10.19457/j.1001-2095.20170201

2016-01-30

修改稿日期：2016-06-21

国家自然科学基金（51377168）；山东省科技发展基金（2011GGH20411）

张华强（1967-），男，博士，教授，Email：zhq@hit.edu.cn