分运动独立的条件和理论基础

王远征

(山东省烟台第二中学 山东 烟台 264000)

分运动独立的条件和理论基础

王远征

(山东省烟台第二中学 山东 烟台 264000)

以微分方程的可加性为基础，论述了分运动独立与否的条件是——合运动的动力学方程可以写成两个分运动的动力学方程之和，为用运动的分解与合成解决复杂的运动指明了理论基础．

分运动的独立性 运动的分解与合成 微分方程的可加性

在研究复杂运动的时候，时常会出现两个分运动相互独立的现象，即：一个分运动的改变并不影响另一个分运动的快慢，于是，有人就得出了“运动的独立性原理”的说法．而实际上，分运动的独立性是有条件的，分运动不独立的现象比比皆是．

【例1】一个小球以水平的初速度v0抛出，其受到的空气阻力和速度的平方成正比，试求该小球在水平和竖直两个方向的运动情况．

分析：物体的动力学方程为

在x方向上，满足的方程为

(1)

同时在y方向上，满足的方程为

(2)

无论我们将两个方程施加何种运算，既不能在方程(1)中消掉vy，也不能在方程(2)中消掉vx，这说明，两个分运动就不是独立的．故而，运动的独立性原理不是一个真正的有普遍意义上的规律．

但是，如果两个分运动要是独立的话，就可以先分别研究出两个分运动的情况，进而求出合运动的情况，不光是我们处理复杂运动的重要手段，而且确实可以使解题过程大为简化，特别是在中学阶段，这几乎是处理复杂运动问题的唯一手段．

【例2】如图1所示，在匀强磁场中由静止释放一个带正电的微粒，证明它的运动轨迹是摆线．

图1 磁场中静止释放正电荷的运动轨迹

分析：微粒的初速度是零，我们将运动是零的状态看作是向左速度v0和向右速度也是v0的两个运动的叠加，并设定v0的大小满足

qv0×B=mg

所以，向右的运动是以v0为初速度的匀速直线运动，向左的运动因为只受洛伦兹力的作用，因而做匀速圆周运动．而这两个分运动的合运动正好组成摆线运动．

我们刚才的计算，就建立在两个分运动的独立性之上．现在，关键的问题是，我们怎么知道这两个分运动是独立的呢？我们的处理方法一定是正确的呢？答案非常简单：我们分别列出两个分运动的动力学方程为

qv0×B+mg=0

(3)

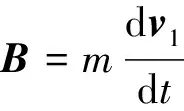
(4)

式中v1代表初速度向左的分运动的速度．而合运动的动力学方程一定可以写成如下的形式

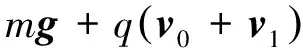
(5)

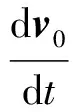
一般的，如果一个运动的动力学方程可以写成两个独立的运动方程之和．则两个分方程解的和就是总方程的解——即两个分方程描述了两个分运动，总方程就描述了物体的合运动．

有了这样的认识，我们在用运动的合成与分解处理复杂的运动时，就不再是仅凭着感觉和臆测，而是有了严密的根据．

2016-11-15)