已知多元变量关系求最值问题的解决策略

江苏省高邮中学 古模楷

已知多元变量关系求最值问题的解决策略

江苏省高邮中学 古模楷

在各地高考以及高考模拟试题中，一类已知多元变量求最值问题的题目通常以填空题的形式出现，这类题目的特点是变量多（通常为2-3个）、形式多样（不等式条件和等式条件），有些题目难度较大，学生解决起来比较困难。笔者根据自己的教学实践，从解决策略的角度对这类问题做了一个归类，与诸位同仁共勉。

策略一：运用整体思想，寻求“结论整体”与“条件整体”之间的关系。

有些题目“条件整体”与所求“结论整体”的关系较为明显，这时只要找到这种关系，就可以选择恰当的方法来解决，在解题方法选择中，往往要遵循“整体运用优先”的原则。

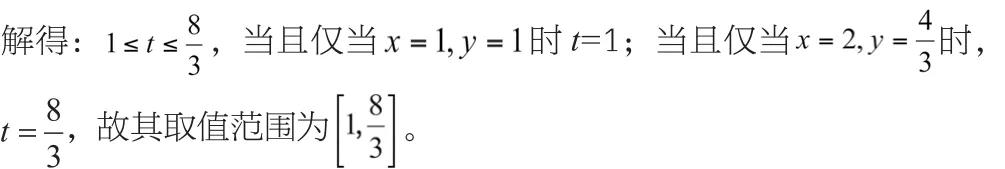
策略二：运用消元思想，将多元问题转化为两元甚至一元问题求解

本题利用条件等式中的关系，将三个变量中的y用另外两个变量x，z来表示，将三维变成了两维，然后直接利用基本不等式求解。

本题为三元变量问题，而且已知条件为不等式形式，无法直接代换消元，这里采用不等式的性质中的两边同乘以一个正数的性质成功将三元代换为两元，这里重心是消元。

策略三：运用转化思想，将代数问题转化为几何问题。

有些问题从代数角度来讲似乎无法处理，这时如果从几何意义的角度看，也许就会峰回路转，立即找到解决问题的方法与技巧。

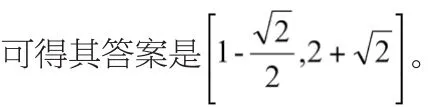
解决本题的关键主要是注意到原式的分式特征，从代数角度无法解决，但联想到直线的斜率特征和分式的特征，从几何角度去看问题就迎刃而解了。

策略四：利用不等关系中的相等条件，取得最值的条件是关键。

对于条件为不等关系的式子，可以抓住其“不等条件”中的“相等关系”来代换消元，但要特别关注最后要求的最值的前提是不等关系中的相等关系必须成立，否则方法失效。

总之，这类问题在高考中时有出现，其难度相对较大，这就要求同学们在平时多思考，善于将题目的条件与结论合理联系与恰当转化，还要善于总结，并在上述几个策略的指导下经过较长期的历练，方可取得理想的效果。