几种预测模型在变形监测数据处理中的应用

刘 阳

(黄河勘测规划设计有限公司，河南 郑州 450000)

几种预测模型在变形监测数据处理中的应用

刘 阳

(黄河勘测规划设计有限公司，河南 郑州 450000)

通过某高层建筑物沉降监测数据，对比分析了GM(1,1)模型、新陈代谢GM(1,1)模型、最优化背景值的新陈代谢GM(1,1)模型和灰时序GM-AR模型的预测精度，得出了GM-AR模型对建筑物沉降预测效果更好的结论。

沉降监测，GM(1,1)模型，新陈代谢GM(1,1)模型，GM-AR模型

0 引言

随着科学技术的不断进步，高层建筑也变得越来越多的被人们采纳，建筑物越高，所在的区域也将承受更多的压力，就会越容易产生沉降及变形，会危及高层建筑及周边的安全。建筑物的变形监测就是在建筑物及其周边区域布设监测点，对监测点进行周期性观测，分析其变化的规律并结合模型预测其变化的趋势，从而得到建筑物的安全状况。本文在灰色模型的基础上，讨论了新陈代谢灰色模型及灰时序GM-AR模型的建模过程，并以某高层建筑物的沉降监测数据为例，对比分析了四种模型的预测精度，从而得到新陈代谢灰色模型、最优化背景值新陈代谢GM(1,1)模型和灰时序GM-AR模型的预测精度较灰色模型都有较大提高。

1 灰色GM(1,1)模型

1.1 灰色GM(1,1)模型

灰色模型，即GM(1,1)模型是对原始数据序列的一次累加和变化，从而生成一组新的数据序列进行建立的。假设原始数列为x(0)={x(0)(1),x(0)(2),x(0)(3)，…,x(0)(n)}，对x(0)进行一次累加变换，从而得到一个新的序列x(1)={x(1)(1),x(1)(2),x(1)(3)，…,x(1)(n)}，进而建立一阶微分方程，则GM(1,1)模型为：

(1)

式(1)中，a与u都是灰参数，由最小二乘法可得：

(2)

(3)

经过累减可得到模型的还原值：

(4)

1.2 灰色GM(1,1)模型的精度检验

经灰色模型GM(1,1)预报后，可以得到原始数列的方差和残差方差。

原始数列的方差：

(5)

残差方差：

(6)

则灰色模型GM(1,1)的精度可以由式(5)和式(6)来计算检验。

后验方差比为：

(7)

小误差概率为：

(8)

一个好的预报模型，要求C越小，P越大。一般按照C，P的取值，将模型的预测精度分为四个等级，见表1。

表1 预测精度等级分类

2 新陈代谢灰色模型

3 最优化背景值的新陈代谢灰色模型

利用背景值取积分的形式导出：

最优化背景值的新陈代谢GM(1,1)模型和新陈代谢GM(1,1)模型相比，只是背景值的选取作了改变，其预测的流程和新陈代谢GM(1,1)模型相同。

4 灰时序GM-AR模型

趋势项提取法，是先从非平稳时间时序样本中提取出确定性部分(变化性趋势项和周期性趋势项)，并用适宜的函数关系式拟合该部分，从原时间序列样本减去该部分，再对剩余的残差序列建立时间序列模型，最终将确定性部分的函数关系式与时间序列模型组合起来，形成组合预报模型。

用灰色模型拟合序列的趋势项，用时序模型拟合波动项，然后取两者之和，公式如下：

Xt=dt+yt。

其中，dt为趋势项；yt为波动项。提取GM(1,1)模型趋势项后与AR(n)模型组合，就可以形成新的预测模型：

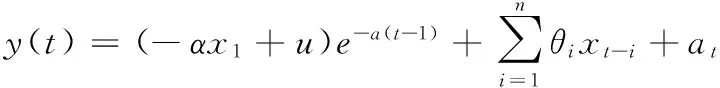
5 实例分析

某高层建筑在建设之初，布设在建筑物上及其周围的沉降监测点共18个，且各监测点需要进行周期性观测，本文采用其中一个点的沉降数据作为实验数据，分别用以上四种模型对其进行预测。此点的原始沉降观测数据如表2所示。

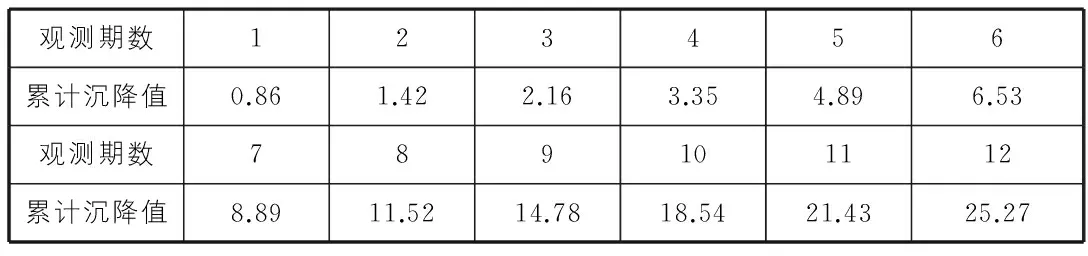
表2 原始观测沉降值 mm

根据表2中的原始观测沉降值，我们采用前六期观测数据分别用以上四种模型进行建模，来预测未来五期的沉降值，并和原始观测值作比较，从而来分析各模型的预测精度。在此定义其相对精度：

p=|I真实值-I预测值|/I真实值。

本文采用以下两种方案对数据序列进行预测：

方案一：GM(1,1)模型和新陈代谢GM(1,1)模型对原始数据进行预测。

方案二：最优化背景值的新陈代谢GM(1,1)模型和灰时序GM-AR模型对原始数据进行预测。

表3 GM(1,1)模型和新陈代谢GM(1,1)模型对比

根据表3可知，GM(1,1)模型和新陈代谢GM(1,1)模型的预测精度都是随着预测时间的增加而逐渐降低，且GM(1,1)模型的预测精度随着预测时间的增加降低的较快，其最大误差为7.8 mm，相对误差达到了30.87%，新陈代谢GM(1,1)模型的最大误差为4.88 mm，最大相对误差为18.99%。所以新陈代谢GM(1,1)模型较GM(1,1)模型的预测精度有了明显地提高。

2)应用方案二得到未来五期的预测值见表4(其中，3代表最优化背景值的新陈代谢GM(1,1)模型，4代表灰时序GM-AR模型)。

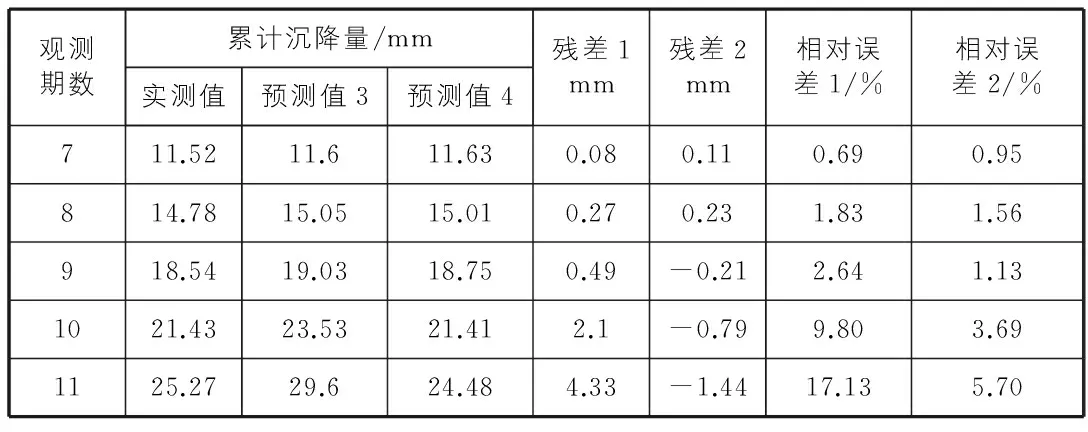
表4 最优化背景值的新陈代谢

由表3和表4可知，最优化背景值的新陈代谢GM(1,1)模型较GM(1,1)模型预测精度有较大提高，同新陈代谢GM(1,1)模型相比，预测精度有一定的提高，但是提高的不是很明显。而灰时序GM-AR模型的预测精度较以上三种都有了较大提高，且模型的收敛性较好，也可以用于中长期预测。

为了便于综合分析，将以上实例分析绘制成如图1所示的曲线。

6 结语

由以上实例分析可知，GM(1,1)模型可应用于高层建筑物的沉降预测，但是随着预测期数的增加，预测精度降低较多。对比GM(1,1)模型，新陈代谢GM(1,1)模型和最优化背景值的新陈代谢GM(1,1)模型预测精度有了一定提高，但收敛性较差。GM(1,1)模型和时序模型组合而成的灰时序GM-AR模型的预测精度较之三种模型都有较大的提高，且GM-AR模型形式简单、收敛性较好，可广泛在建筑物变形监测数据处理与预测中应用。

[1] 邓聚龙.灰理论基础[M].武汉：华中科技大学出版社,2002.

[2] 王正新.GM(1,1)模型的特性与特性优化研究[D].南京:南京航空大学,2007：31-32.

[3] 邓聚龙.灰色系统论文集[M].武汉：华中理工大学出版社,1989.

[4] 侯建国,王腾军.变形监测理论与应用[M].北京:测绘出版社,2008.

[5] 郭齐胜.系统建模原理与方法[M].长沙:国防科技大学出版社,2003.

[6] 兰孝奇,杨永平,黄 庆,等.建筑物沉降的时间序列分析与预报[J].河海大学学报(自然科学版),2006,34(4):426-429.

[7] 曾 山,徐 兮.基于AR模型的填方路基沉降检评方法[J].重庆交通大学学报(自然科学版),2013(10):91-92.

The application of several prediction models in deformation monitoring data process

Liu Yang

(TheYellowRiverPlanning&DesignLimitedCompany,Zhengzhou450000,China)

Through the settlement monitoring data of a high-rise building, this paper comparatively analyzed the GM(1,1) model, metabolism GM(1,1) model, optimization background value metabolism GM(1,1) model and grey temporal GM-AR model prediction precision, gained the conclusion of GM-AR model had better prediction effect to building settlement.

settlement monitoring, GM (1,1) model, metabolism GM(1,1) model, GM-AR model

1009-6825(2017)02-0219-03

2016-11-02

刘 阳(1990- )，男，助理工程师

TU198

A