地面式钢筋混凝土圆形水池液固耦合模态分析★

高 霖 王明振,2

(1.重庆文理学院建筑工程学院，重庆 402160； 2.中国地震局工程力学研究所 中国地震局地震工程与工程振动重点实验室，黑龙江 哈尔滨 150080)

地面式钢筋混凝土圆形水池液固耦合模态分析★

高 霖1王明振1,2

(1.重庆文理学院建筑工程学院，重庆 402160； 2.中国地震局工程力学研究所 中国地震局地震工程与工程振动重点实验室，黑龙江 哈尔滨 150080)

对地面式钢筋混凝土圆形水池进行了考虑液固耦合效应的模态分析，并使用ADINA有限元软件，分析了储液状态、储液高度、水池半径以及液体表面重力波对模态的影响，对比了储液晃动频率的理论和有限元计算结果，推导得到了水池储液晃动基本周期计算公式。

水池，液固耦合，ADINA，模态分析，晃动周期

0 引言

给水系统是典型的城市生命线系统，是城市健康运营的物质基础。生命线系统的功能以整个系统的运营状态为体现，其中每一个环节对整个系统的功能均有不可忽略的作用。给水系统功能有取水、储水、净水和输配水。给水系统中，完成储水和净水功能角色的则是水池，水池是给水系统中的重要构筑物，对整个系统的功能有重要影响。历次地震震害表明：水池结构在强烈地震作用下易发生不同程度的破坏。结构的模态特性对其在地震作用下的响应有重要影响。通过模态分析可以得到结构的频率、振型及模态参与质量等动力特性，由动力特性根据反应谱可确定结构的地震影响系数。1957年，Housner教授对刚性储液结构的模态和液动压力进行了分析[1]，后续较多专家学者也对储液结构模态进行了分析[2-5]，但大多数结果是针对刚性储液结构给出的。我国GB 50032—2003室外给水排水和燃气热力工程抗震设计规范中尚未给出储液水池的模态计算方法，不便于储液水池的地震响应计算。同时，由于水池这类结构在正常使用时包括固体结构和液体两相，内部液体的存在会影响水池结构的模态特性，因此在研究储液结构模态特征时必须考虑两相间液固耦合效应的影响。

综上所述，为了得到合理的储液水池模态分布特征，本文使用ADINA有限元软件和理论公式法对地面式钢筋混凝土圆形水池进行考虑液固耦合效应的模态分析，研究模态分布的规律，为计算储液水池的地震响应奠定基础。

1 液固耦合水池有限元模型

水池结构尺寸的确定主要参照相关规范、图集和实际工程案例，所分析水池的结构形式均为地面式、无顶盖的圆形水池。将水池的结构形式、名称、容量、底厚、壁厚、储液半径、最大储液高度及配筋等基本参数列于表1中。为分析不同储液量对水池振动模态的影响，同时考虑水池的日常工作状态，选取从无水至70%储液量之间共8个储液工况(如表2所示)对水池A，B，C分别进行模态分析。为便于分析结果的表述，使用编号“C-70%”表示容量2 000 m3水池、储水高度为2.45 m的工况，其他工况以此类推。ADINA中液体材料的密度为1 000 kg/m3，体积模量2.3×109Pa，阻尼比0.16%[6]。

表1 圆形水池基本参数

表2 储水量与储水高度对应表

使用ADINA Parasolid几何建模方式建立水池模型。液体采用3D-Fuild势流体单元，可模拟与结构单元的耦合问题。池体结构采用3D-Solid单元，为混凝土材料，使用Truss单元中的Rebar选项设置钢筋[7]。模型网格划分时兼顾计算精度和速度。根据研究对象的特点，选用行列式搜索法(Determinant-Search Method)进行模态分析，同时得到模态参与因子，用以表征某阶模态对结构振动的贡献程度。

2 模态计算结果分析

进行液固耦合系统模态分析时，首先对模型施加重力荷载进行静力分析，在模态分析时选择静力计算结果进行重启动，进行模态和参与因子计算。3种不同尺寸水池、8种储液状态、是否考虑表面重力波影响2种情况，共计算48个工况。对比分析各工况的计算结果，分析不同因素对模态的影响程度和趋势。

2.1 储液状态对模态的影响

计算无液和储液状态时水池的模态，分析储液状态对模态的影响。无液时，水池的振型主要为池壁的振动，且振动频率较高。当水池内储有液体时，无论储液量的多少，液固耦合系统包括刚体模态、储液低阶晃动模态和结构高阶振动模态三种。模态计算时第一阶模态为刚体模态，其频率非常小，无限接近于零，主要表现为流体所有节点上的压力值相同，固体结构在均布内压下的变形，刚体模态的参与质量百分比几乎为零。以A-50%工况为例，图1为其刚体模态。从第二阶开始直至结构高阶振动模态之间全部为储液晃动模态，储液晃动模态的频率相对较小，主要表现为池内液体的晃动，水池结构虽在晃动压力下变形，但相对液体晃动而言，池壁的振动响应是微小的。图2为A-50%工况的储液晃动一阶模态。结构振动模态频率较高，不易被激发，主要表现为池壁的振动，池内液体为脉冲模态，结构一阶振动模态如图3所示。当储液量不同时，出现结构振动模态的阶数略有差异。

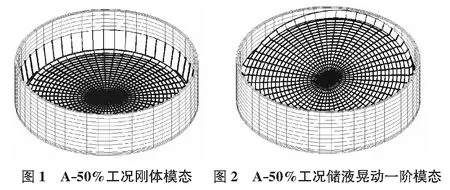
对比分析各工况模态计算结果可知：液体的存在改变了结构的振动模态，由单一的结构振动转变为包括刚体模态、储液低阶晃动模态和结构高阶振动模态三种。不同储液量时，相同阶数三种模态的振型几乎完全相同；储液时的结构高阶振型与无液时的结构振型几乎完全相同，且出现的顺序基本相同。储液水池的储液晃动模态很容易被激发，且其振型参与质量较大，对结构的振动响应影响较大。由于结构的旋转对称性，振动模态大多成对出现，仅振型方向不同。

2.2 储液高度对模态的影响

将A水池不同储液高度下的刚体模态频率、前三阶储液晃动频率和结构高阶振动频率列于表3中。

表3 A水池不同储液高度时若干阶模态频率

Hz

从表3中可以看出：储液时的第一阶模态均为刚体模态，其频率无限小接近于零；随着储液高度的增大，同一阶次的储液晃动频率逐渐增大，且储液高度越大，数值增大越缓慢；对比结构振动频率的变化趋势可以分析液体对结构振动的影响，同一阶次结构振动频率随着储液高度的增大而不断减小，说明储液高度越大，液体对结构振动的影响程度越大，使得液固耦合效应越显著。

2.3 液体表面重力波对模态的影响

表面重力波存在于液体和气体两种流体的分界面上，以表面波的形式存在，并以重力为恢复力[8]。前述计算水池动力特性时均考虑了液体表面重力波，即液面为自由液面，其约束为Free Surface。当约束住液面的Z向位移，即约束了液面的自由晃动，也即不考虑液体表面重力波，通过ADINA计算可直接得到结构振动模态。将水池A储水高度为10%，30%，50%和70%的考虑和不考虑液体表面重力波时的结构振动频率列于表4中。

表4 考虑和不考虑液体表面重力波时水池A的结构振动频率 Hz

从表4中可以看出：储液高度相同时，对于同一阶结构振动频率，考虑液体表面重力波比不考虑时的略小，但相差甚微，说明表面重力波对结构振动模态有一定的影响，但影响程度较小。同时发现考虑与不考虑表面重力波时的模态振型基本相同，这与文献[9]的研究结果相同。因此，求解结构模态时可以不考虑液体表面重力波的影响。由于约束了液面的Z向位移，不考虑液体表面重力波时得不到储液晃动模态。

2.4 水池半径对模态的影响

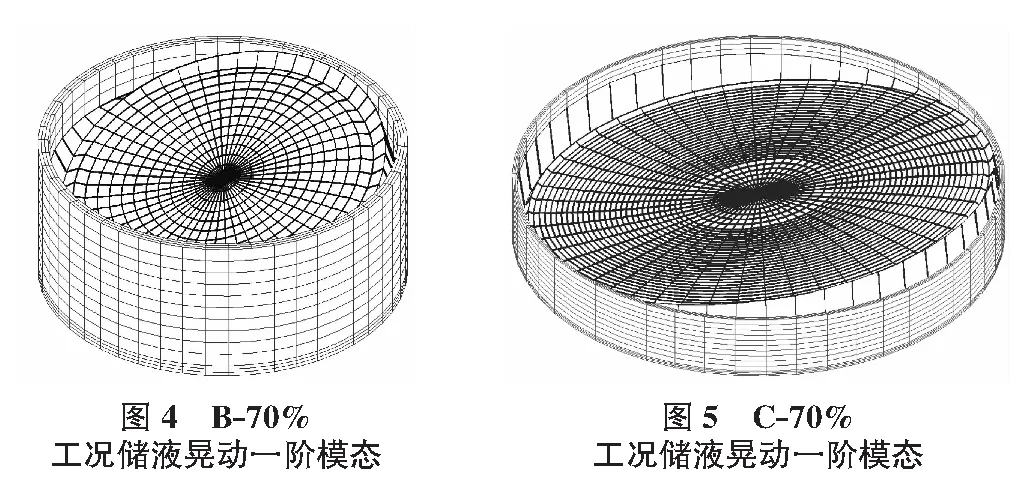
将储液高度为70%的A，B和C水池前三阶储液晃动频率和结构振动频率列于表5中。计算时均考虑液体表面重力波。

对于储液晃动模态，从表5中可以看出，储液晃动频率数值随水池半径的增大而减小；对比图2，图4和图5，水池半径不同时同一阶储液晃动振型基本相同。对于结构振动模态，频率数值也随水池半径的增大而减小，水池半径越大，液固耦合效应越显著；水池半径不同时，结构振动振型被激发的顺序不同。水池半径对储液晃动和结构振动频率均有影响，水池半径对储液晃动振型影响较小，对结构振动振型影响较大。

表5 储液高度70%的水池A，B和C的模态频率计算结果 Hz

3 储液晃动频率有限元法和理论法计算结果对比

GB 50032—2003室外给水排水和燃气热力工程抗震设计规范中尚未给出储液水池晃动基本周期计算公式。文献[3]中给出了基于如下假定的储液结构内液体振动频率计算公式，见式(1)，认为储液结构为绝对刚体，液体为无粘、无旋、不可压缩的理想液体，且做小振幅运动。

(1)

由式(1)计算所分析水池的储液晃动频率，列于表6中，并与ADINA计算结果进行对比。

表6 储液晃动频率理论与有限元计算结果对比 Hz

从表6中可以看出：不同储液高度、不同水池半径下，储液晃动前三阶频率的理论和ADINA计算结果相差很小，也说明了所建立的有限元模型合理可靠。由于有限元计算时储液结构具有一

定的弹性模量，而并非刚性，液面为自由液面且考虑表面重力波的影响，使得两种方法计算的频率值有一定的差异。基于上述分析，推导得到圆形水池储液晃动基本周期计算公式，见式(2)。储液晃动基本周期是计算储液结构地震响应的重要参数。

(2)

其中，T1为储液晃动基本周期，s；R为储液半径，m;HW为储液高度，m。

4 结语

本文对地面式钢筋混凝土圆形水池进行了考虑液固耦合效应的模态分析，主要得到以下5条结论：1)储液结构由于内部液体的存在，改变了结构的动力特性。储液结构模态包括刚体模态、以液体晃动为主的储液低阶晃动模态和以结构振动为主的结构高阶振动模态三种。2)水池半径相同时，储液高度越大，同一阶次储液晃动频率越大，同一阶次结构振动频率越小。储液高度越大，液固耦合效应越显著。3)液体表面重力波对储液结构模态影响较小。不考虑液体表面重力波时，ADINA软件可直接求得结构振动模态。4)储液高度相同时，水池半径越大，同一阶次储液晃动频率和结构振动频率越小，储液晃动振型基本相同，但结构振动振型被激发的顺序不同。5)有限元法和理论法计算储液晃动频率相差很小，验证了所建立有限元模型的可靠性。推导得到了水池储液晃动基本周期计算公式，可用于水池结构地震响应计算。

[1] Housner GW.Dynamic pressures on accelerated fluid containers[J].Bulletin of the Seismological Society of America,1957,47(1):15-35.

[2] Haroun MA.Vibration studies and tests of liquid storage tanks[J].Earthquake Engineering and Structural Dynamics,1983,11(2):179-206.

[3] 居荣初,曾心传.弹性结构与液体的耦联振动理论[M].北京：地震出版社,1983.

[4] 项忠权,李清林.立式储罐抗震[M].北京：地震出版社,1990.

[5] 陈志涛.卵形消化池流—固耦合系统的ADINA有限元分析[D].天津:天津大学,2007.

[6] 沈世杰.贮水池动水压力计算探讨[J].特种结构,1995,12(4):4-7.

[7] ADINA北京代表处.ADINA土木工程分析实例手册[M].北京:ADINA代表处,2005.

[8] 高 霖.地面式钢筋混凝土水池自愈、渗漏试验及地震响应分析[D].哈尔滨:中国地震局工程力学研究所,2015.

[9] 舒亚俐.考虑液固耦合振动的贮液结构动力特性和地震响应研究[J].特种结构,2013,30(1):69-75.

The modal analyses considering liquid-structure coupling effect of ground reinforced concrete circular tanks★

Gao Lin1Wang Mingzhen1,2

(1.CollegeofArchitectureEngineering,ChongqingUniversityofArtsandSciences,Chongqing402160,China; 2.InstituteofEngineeringMechanics,ChinaEarthquakeAdministration,KeyLaboratoryofEarthquakeEngineeringandEngineeringVibration,ChinaEarthquakeAdministration,Harbin150080,China)

The modal of ground reinforced concrete tanks are analyzed considering liquid-structure coupling effects. The influence of liquid state, liquid height, tank radius and surface gravity waves on modal are analyzed by using ADINA software. And the theory and finite element calculation results of sloshing frequency are compared. And the sloshing foundation period formula of circular reinforced concrete tank is derived.

tank, liquid-structure coupling, ADINA, modal analysis, sloshing period

1009-6825(2017)02-0047-03

2016-11-08★：重庆文理学院校级科技项目(项目编号：R2015JJ06)；国家自然科学基金资助项目(项目编号：51678544)；国家科技支撑计划课题(课题编号：2015BAK17B05)

高 霖(1988- )，女，博士，讲师

P315.8

A