基于PSO-SVM的四旋翼航向角误差补偿研究

王鹏彰， 孙美玲

(南京理工大学 自动化学院 控制理论与控制工程系，江苏 南京 210094)

基于PSO-SVM的四旋翼航向角误差补偿研究

王鹏彰， 孙美玲

(南京理工大学 自动化学院 控制理论与控制工程系，江苏 南京 210094)

针对强电磁干扰对四旋翼航向角产生较大影响，分析了多数文献提出的航向角误差补偿方法的不足，提出了一种基于粒子群优化(PSO)的支持向量机(SVM)的航向角误差补偿方法。在强电磁干扰下，建立了以测量航向角为输入，期望航向角为输出的误差补偿模型，并利用采集的数据进行仿真验证。结果表明，该模型可靠并大大提高了航向角精确度。

粒子群优化算法； 支持向量机； 强电磁干扰； 四旋翼； 航向角； 误差补偿

0 引 言

目前，关于电子罗盘误差补偿的方法，文献[3]采用最小二乘法进行误差补偿，运算复杂并且面对非线性易发散而得不到最优解。文献[4]采用基于最小二乘的分段补偿方法，主要针对水下工作的电子罗盘误差补偿。文献[5]采用基于径向基函数(RBF)神经网络的电子罗盘误差补偿方法，虽然神经网络具有很好的非线性映射能力和很强的自适应、自学习能力，但是神经网络需要大量的训练样本，其网络结构依靠经验，具有一定的盲目性，并且不太稳定。

针对以上出现的问题，本文提出了基于粒子群优化(particle swarm optimization,PSO)的支持向量机(support vector machines，SVM)航向角误差补偿方法，建立了以测量航向角为输入，期望航向角为输出的误差补偿模型。相对于神经网络而言，SVM具有严谨的理论知识和数学基础，克服了局部最小点、过学习等缺陷，适用于小样本、非线性机器学习问题[6]。利用PSO算法寻找SVM最优参数，有效地解决了参数选择问题，提高了航向角精确度。

1 误差分析

电子罗盘的误差来源可以分为三类：其一自身误差，主要包括制造误差和安装误差，一般对测量精度的影响较小。其二硬磁干扰，源于载体上的永久磁铁或者被磁化的金属等硬磁材料，其磁场相对稳定，分布均匀，本实验使用的电磁铁便属于硬磁干扰。其三软磁材料，软磁材料本身不产生磁场，但是它被环境磁场磁化后又影响其周围磁场，其大小随外界磁场变化而变化，比较复杂但相对于电磁铁等硬磁材料的影响较小[3,7]。

2 基于PSO算法的SVM

实践表明，SVM的性能与核函数的类型、核函数的参数和惩罚系数c有很大关系。通常人们进行大量实验直观简单地获得较优参数，但耗费了大量的时间和精力。PSO算法作为寻优优化算法，概念清新、效率高，可以很好地选择SVM最优参数。

2.1 SVM

SVM是一种基于统计学习理论的机器学习方法，能较好地解决小样本、非线性等实际问题[8]。SVM回归算法的基本思想是将给定的观测数据x通过非线性φ映射到高维特征空间，然后进行线性回归。利用式(1)进行回归估计

经历了国庆期间的一波疯涨之后，尿素价格再次回归平稳震荡区间，在2100元/吨左右的价格小幅震荡，跌跌涨涨不断。国庆期间尿素价格大幅上涨的原由已不必再做分析。国庆后，各国招标相继结束，国内尿素价格出现小幅回落，而后在上游厂家的惜售挺价操作下，又有所上调。可以看出，在失去了国际市场的强硬利好支撑之后，国内市场的促涨动力显出了疲态，市场再次进入僵持阶段，且预计将维持一段时间。

f(x)=(w,φ(x))+b

(1)

式中w和b为回归因子，通过最小化正则化风险泛函得

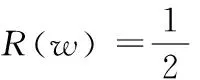
(2)

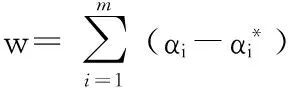
(3)

式中 k(xi,x)=(φ(xi;φ(x)))为核函数，常用的核函数有线性核函数、多项式核函数、径向量基函数(radialbasisfunction,RBF)核函数等[9]。由此看出惩罚因子和核函数参数对SVM的性能的重要性。

2.2PSO

PSO算法是一种基于群体智能的全局随机搜寻算法。粒子群初始化一群随机粒子(随机解)，通过迭代找到最优解。在每一次迭代中，粒子通过跟踪两个极值来更新自己的速度和位置。一个极值是粒子本身找到的最优解，称为个体极值Pbest,另一个极值是整个种群目前找到的最优解，称为全局极值Nbesti，每个粒子根据式(4)和式(5)来更新自己的速度和位置

V=wgV+c1r1(Pbest-X)+c2r2(Nbest-X)

(4)

X=X+βgV

(5)

式中 V指粒子的速度，其决定粒子的走向和位置，P指粒子当前位置和SVM优化参数值，w称为惯性因子，c1和c2是加速常量，r1和r2是介于0和1之间的随机数。β是约束因子[10]。

2.3PSO算法优化的SVM

SVM选用常用的RBF核函数，运用PSO算法对SVM的惩罚因子c和RBF核函数的参数g进行寻优，基于PSO的SVM的流程具体步骤如下：

1)初始化参数。初始化种群规模、迭代次数、加速参数等。

2)计算每一个粒子适应度。

3)更新粒子的个体极值和全局极值。

4)用式(4)和式(5)更新每一个粒子的速度和位置。

5)如果当前的迭代次数达到了预先设定的最大次数或达到最小误差要求，则停止迭代，输出最优解；否则，转到步骤(3)。

6)获得此次最优的SVM惩罚因子参数c和核函数参数g。

7)获得PSO算法优化的SVM回归机。

3 仿真实验与结果分析

本实验选用的是Pixhawk四旋翼飞行器，其电子罗盘型号为LSM303D，电磁铁采用的是伊莱科电气有限公司的产品，型号是ELE-P20/15。电磁铁安装在四旋翼飞行器的正下方，距离传感器距离大约15cm。将四旋翼飞行器放置在水平转台上，每15°记录一次在强磁干扰下的测量航向角和期望航向角，共24组实验数据作为SVM的训练样本，如表1所示。为验证本方法的有效性和准确性，又随机记录了10组数据作为测试样本。

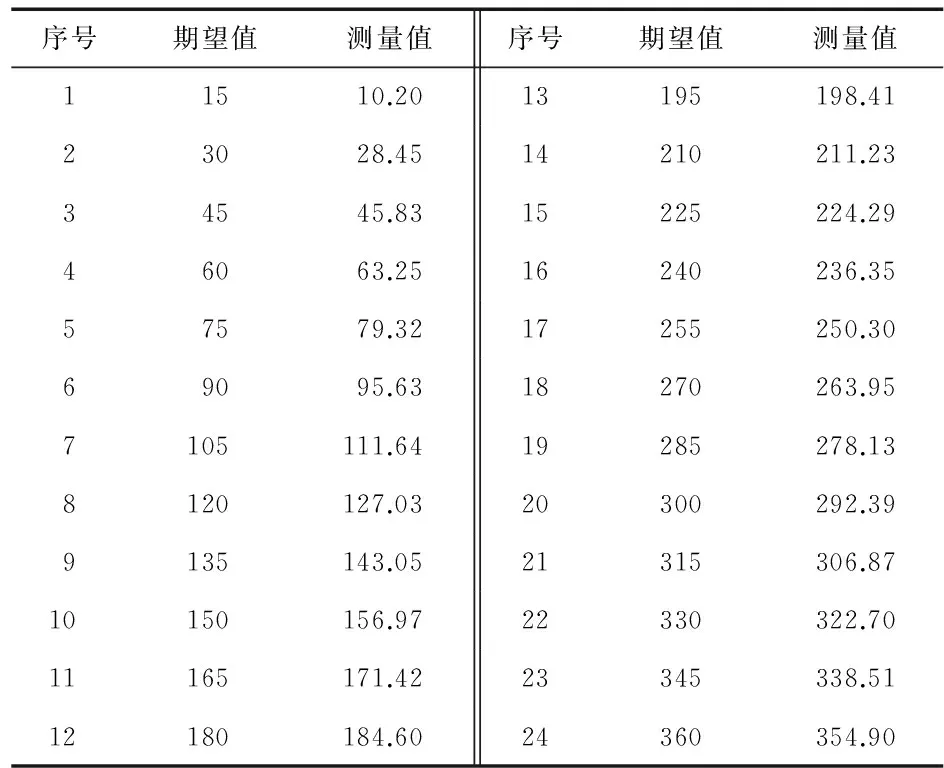
表1 训练样本数据

表1中期望值指航向角的理想值，测量值是指在在电磁铁通电时测得的存在较大误差的航向角。PSO算法的迭代次数为300，c1和c2加速度参数为1.5和1.7，粒子群寻优的适应度曲线如图1所示。

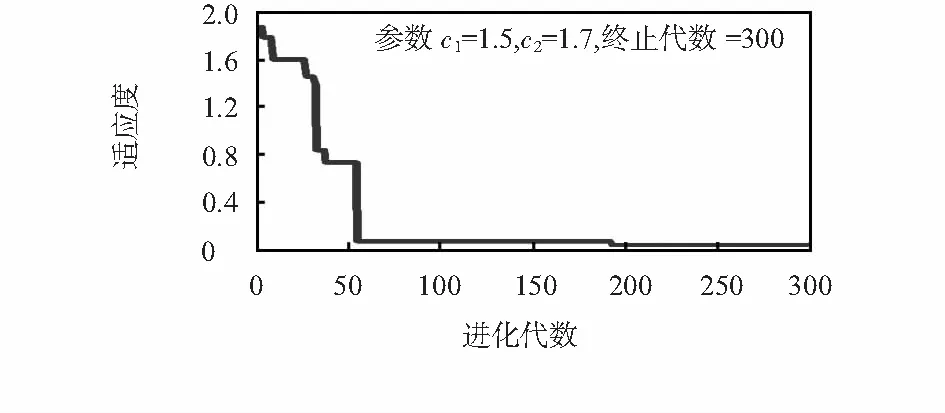
图1 粒子群适应度曲线

图1中PSO时的适应度曲线即参数寻优时SVM的均方差曲线，通过PSO算法得到，SVM惩罚因子参数c为975.209 2，RBF核函数参数g=0.196 6。利用训练好的SVM对测试样本进行仿真，结果如表2所示。

表2 测试结果

表2中期望值指航向角的理想值，测量值指在电磁铁通电时测得的存在较大误差的航向角，补偿值指经过本模型补偿过的航向角。由此可以看出，在机载电磁铁强电磁干扰下，经过基于PSO的SVM航向角补偿模型后，其误差基本可以控制在0.5°以内，不仅精度高而且稳定可靠。

4 结束语

本文结合实际比赛与应用，四旋翼飞行器机载电磁铁时的强磁干扰导致航向角出现较大误差，为减小机载电磁铁的影响，采用基于PSO的SVM算法对航向角误差进行补偿。经验证，本方法不仅工程实现简单、模型稳定可靠，并且提高了在强电磁干扰时航向角精度。

[1] Xiong J J,Zheng E H.Position and attitude tracking control for a quadrotor UAV[J].ISA Transactions,2014,53(3):725-731.

[2] Derafa L,Benallegue A,Fridman L.Super twisting control algorithm for the attitude tracking of a four rotors UAV[J].J Frankl Inst,2012,349:685-99.

[3] 邵婷婷,马建仓,胡士峰,等.电子罗盘的倾斜及罗差补偿算法研究[J].传感技术学报,2007(6):1335-1337.

[4] 张爱军,王昌明,赵 辉.三轴电子罗盘的磁航向角误差补偿研究[J].传感器与微系统,2008,27(8):33-35.

[5] 邵婷婷,樊延虎,林开东.基于RBF神经网络的电子罗盘误差补偿研究[J].电子测量技术,2014(3):36-38.

[6] 黄晨华,谢存禧,张 铁.支持向量机回归算法在机器人误差补偿中的应用研究[J].机床与液压,2009(1)2:47-51.

[7] 叶 健.带倾角补偿的数字式电子磁罗盘设计[D].南京：南京理工大学,2013.

[8] Basak D,Pal S,Patranabis D C.Support vector regression[J].Neural Information Processing—Letters and Reviews,2007,11(10):203-224.

[9] 赛 英,张凤廷,张 涛.基于支持向量机的中国股指期货回归预测研究[J].中国管理科学,2013(3):35-39.

[10] 邵信光,杨慧中,陈 刚.基于粒子群优化算法的支持向量机参数选择及其应用[J].控制理论与应用,2006(5):740-743，748.

Research on error compensation of four rotor heading angle based on PSO-SVM

WANG Peng-zhang， SUN Mei-ling

(Department of Control Theory and Control Engineering，School of Automation，Nanjing University of Science & Technology，Nanjing 210094，China)

Aiming at strong electromagnetic interference has big influence on four-rotor heading angle,analyze deficiencies of methods that most literatures suggest,propose a method of using support vector machine(SVM)based on particle swarm optimization(PSO).The input of the modle is the heading angle that is measured in strong electromagnetic interference,and the desired angle is the output.Through the simulation with the collected data,the results show that the model is reliable and greatly improving the accuracy of the heading angle.

particle swarm optimization(PSO)algorithm; support vector machine(SVM); strong electromagnetic interference; four-rotor; heading angle; error compensation

10.13873/J.1000—9787(2017)03—0048—03

2016—03—31

TP 212

A

1000—9787(2017)03—0048—03

王鹏彰(1991-)，男，硕士研究生，研究方向为组合导航定位技术。