基于手眼标定方程AX=XB的精度影响因素研究*
尚忠义, 董明利, 李伟仙, 李 巍
(1.北京信息科技大学 光电测试技术北京市重点实验室,北京 100192;2.北京邮电大学 信息光子学与光通信研究院,北京 100876)
基于手眼标定方程AX=XB的精度影响因素研究*
尚忠义1, 董明利1, 李伟仙1, 李 巍2
(1.北京信息科技大学 光电测试技术北京市重点实验室,北京 100192;2.北京邮电大学 信息光子学与光通信研究院,北京 100876)
机器人手位姿数据对手眼标定精度的影响不可忽略,将对基于手眼标定方程AX=XB的精度影响因素进行分析。通过手眼标定仿真和实测实验验证上述两个因素对手眼标定精度的影响与理论分析的一致性。通过仿真与实测实验,总结得出了减小摄像机与靶标间距离、减小机器人手的运动前后到基坐标空间距离的相差距离,可提高手眼标定精度,通过四元数法和矩阵直积法验证了此规律在解AX=XB标定方程时的通用性,并且在摄像机与靶标间距约为230 mm以及机器人手的运动前后到基坐标空间距离的相差距离为3.240 1 mm时,手眼标定平移向量相对误差最高精度可达0.040 3 %。
手眼标定; 机器人; 精度评价; 标定方程
0 引 言
手眼标定是确定机器人末端执行器坐标系与固定在其上摄像机坐标系之间的刚性变换矩阵的过程,是计算机视觉领域中一个热点问题,广泛应用于主动视觉、三维测量与重建领域。
手眼标定是由Tsai R Y等人[1]首先提出,其将手眼标定问题转化为求解齐次矩阵方程AX=XB问题,并将手眼标定矩阵分成两步来求解,这种方法计算简单,但是旋转矩阵误差会传递给平移向量。在求解矩阵方程时,Chou J C K[2]基于四元数原理采用奇异值分解的方法分步线性求解手眼关系,此方法将旋转矩阵和平移矩阵同时求解。文献[1~8]主要利用数学工具求解手眼标定方程来提高手眼标定精度,至今该领域研究相对成熟,精度提升空间有限。
目前,通过约束机器人运动方法提高手眼标定精度是手眼标定中一个重要的研究方向。马颂德[9]提出通过控制机器人做些典型运动约束来求解手眼关系。Schimidt J[10]指出标定数据同样会影响最终的手眼标定精度。Shi F H[11]提出了一种运动机制进而提高了手眼在线标定精度。邹劲松[12]采用定点变位姿的方法对手眼关系求解的精度进行分析。Tsai R Y[1]根据公式理论推导出影响手眼标定精度的四个原则,根据这四个原则筛选位姿数据,可提高手眼标定精度。但是Tsai文献中只做了大量的仿真实验,缺乏相应测量环境下的实测实验。
本文根据Tsai手眼标定精度影响因素分析模型,结合搭建的测量系统并基于仿真和实测实验研究基于手眼标定方程AX=XB的精度影响因素。
1 手眼标定精度影响因素分析
Tsai R Y[1]在手眼标定精度的影响因素方面做了理论分析,列出旋转矩阵和平移向量的不确定度公式如下
(1)
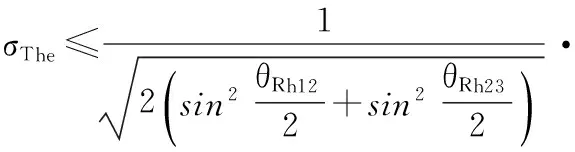
(2)

通过式(1)和式(2)进行分析,可以得到以下提高手眼标定精度的因素:1)调整摄像机和靶标间的距离(定义为因素①)使其最小;2)调整末端机器人手运动前后到基坐标的距离(定义为因素②)相差最小;3)增大机器人手相对运动旋转轴间的角度(定义为因素③);4)增大机器人手两次相对运动的旋转角度(定义为因素④);4个因素如图1所示,图1中①、②、③、④分别对应上面4个因素。

图1 4个因素示意图
Tsai R Y[1]中指出式(2)中|Te1|与|Th1-Th2|比∠(kh12,kh23)和θRe12产生较大的误差,以Tsai R Y文章中结论为依据得出:因素①和②相对手眼标定精度影响比③和④大。本文针对因素①和②进行研究,将通过仿真和实测实验验证上述规律同样也适用于四元数法和矩阵直积法。
2 实验结果与分析
2.1 精度评价方法
使用目前最常用的以目的为导向的精度评价方法进行精度评估[4]。根据已标定的手眼关系和机器手运动模型提供的变换矩阵,计算摄像机变换矩阵的估计值,将测量数据中的每个测量值与对应的估计值相比较,定义旋转和平移的误差如下

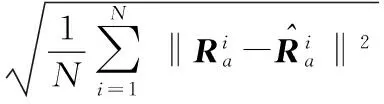
(3)

2.2 仿真实验
本文对Tsai R Y[1]文章的仿真思想进行改进,并在所搭建系统要求的基础上做仿真,同时采用四元数法和矩阵直积法处理仿真数据。将仿真影响手眼标定精度的因素表示如下:因素①:摄像机与靶标间距|Te|。因素②:机器人手运动前后到基坐标空间距离相差距离|Th1-Th2|。
2.2.1 因素①仿真实验
因素①仿真实验即仿真摄像机与靶标间距对手眼标定精度的影响。针对手眼标定模型AX=XB,由于实际测量中摄像机到靶标间距离(即为Ci的平移向量的模)变化范围为300 %,仿真过程中将Ci的平移向量的模从0 %~320 %以80 %为步进值放大,即将摄像机与靶标的间距放大。仿真过程如下:设定手眼标定真值X,给定一组满足实际的测量要求数据Ci(i=1,2,…,n-1),计算Ai=Ci+1(Ci)-1(i=1,2…n-1),以及B=X-1AX。在Ci的旋转轴上从0 %~6 %以0.5 %为步进值加高斯噪声,根据AX=XB分别用三种算法标定X;最后增大Ci平移向量的模为原始量的80 %,计算得到Ai和Bi,依此类推增大Ci平移向量的模为160 %,240 %,320 %时按上述仿真过程进行仿真。
由图2可知,三种方法中随着Ci平移向量的模逐渐增大即摄像机与靶标间距增大,平移向量相对误差增大,因此,减小摄像机与靶标的间距可使手眼标定精度提高。
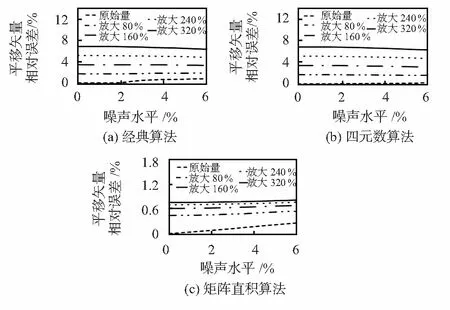
图2 因素①对手眼标定精度影响
2.2.2 因素②仿真实验
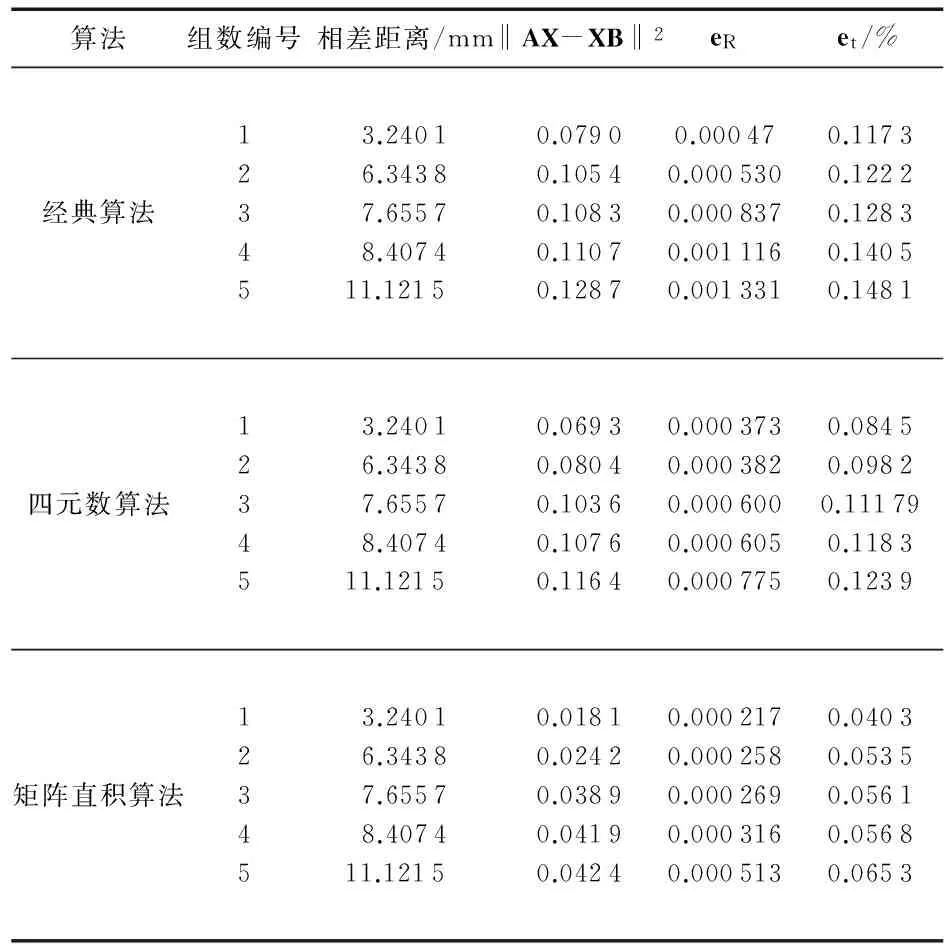
因素②仿真实验即为机器人手运动前后到基坐标空间距离相差距离。针对因素②对手眼标定精度影响做仿真实验,根据位置到机器人基坐标距离远近,将位置分为3个范围,分别以半径r1,r2,r3为约束(其中,r1 图3 仿真位姿示意图 图4 因素②对手眼标定精度影响 由图4可知,三种算法从集合P1与P2筛选的位置比集合P1与P3筛选的位置的AX=XB标定误差小,因此,减小机器人手运动前后到基坐标空间距离相差距离,可使手眼标定精度提高,此规律适用于经典算法,同时也适用于四元数方法和矩阵直积方法。 2.3 实测实验 为了验证仿真实验的结果,以DENSO的VS—6577GM型号的机器人为基础平台,在其机器人手末端安装摄像机,摄像机型号为凯视佳UD274M/C,其分辨率为1 628 pixel×1 236 pixel像元尺寸为4.4 μm,选用COMPUTAR 12 mm镜头。图5(a)是在3 mm×3 mm棋盘格平面靶标,设其为靶标1下的实测实验图,图5(b)在11 mm×11 mm棋盘格平面靶标,设其为靶标2下的实测实验图,图5(c)是在23 mm×23 mm棋盘格平面靶标,设其为靶标3下的实测实验图。 图5 棋盘格平面靶标下实测实验 2.3.1 因素①实测实验 因素①实测实验中,根据现有的3个靶标,设计了3组实验:摄像机坐标系到靶标坐标系的距离约为230,540,630 mm时,分别使用靶标1、靶标2、靶标3。为比较在因素①对手眼标定精度的影响,那么在三种靶标情况下各做5组实验求各个误差的平均值,以目的为导向的精度评价方式误差比较结果如表1所示。 表1 摄像机与靶标间距对手眼标定精度影响的误差比较 由表1可知,三种算法都随着摄像机与靶标间距的增大,误差逐渐增大。三种算法,在摄像机坐标系到靶标坐标系的距离约为230 mm时,平移向量相对误差最高精度为0.370 1 %;在摄像机坐标系到靶标坐标系的距离约为540 mm时,平移向量相对误差最高精度为0.503 4 %;在摄像机坐标系到靶标坐标系的距离约为630 mm时,平移向量相对误差最高精度为0.805 3 %,因此,摄像机与靶标间距离越小,手眼标定精度越高。 2.3.2 因素②实测实验 使用靶标1做因素②对手眼标定精度影响的实测实验,在摄像机与靶标的间距约为230 mm,采集15次,即各组位姿示意图如图6所示,机器人手位姿任意三个位姿组合,因此有15×14×13/3×2=455组组合,将455组组合按误差从小到大排序,筛选误差较小的前5组数据比较机器人手运动前后到基坐标空间距离相差距离对手眼标定精度影响,如表2所示。 图6 各组位姿示意图 由表2可知,三种算法都随着运动前后相差距离的增加,误差逐渐增大。因此,机器人手运动前后到基坐标空间距离相差距离较小时手眼标定精度高,在机器人手眼标定过程中减小机器人手运动前后到基坐标空间距离相差距离,可提高手眼标定精度。 表2 因素②对手眼标定精度影响的误差比较 本文针对机器人非接触测量中的手眼标定问题,在Tsai R Y[1]手眼标定算法的基础上通过仿真实验和实测实验分析影响手眼标定的因素,总结得到影响手眼标定精度两个关键因素,即在手眼标定过程中,减小摄像机与靶标间距离、减小机器人手的运动前后到基坐标空间距离相差距离可提高手眼标定精度,同时通过四元数法和矩阵直积法验证了此规律在解AX=XB标定方程时的通用性,并且在摄像机与靶标间距约为230 mm以及机器人手的运动前后到基坐标空间距离的相差距离为3.240 1 mm时,手眼标定平移向量相对误差最高精度可达0.040 3 %。 [1] Tsai R Y,Lenz R K.A new technique for fully autonomous and efficient 3D robotics hand/eye calibration[J].IEEE Transactions on Robotics and Automation,1989,5(3):345-358. [2] Chou J C K,Kamel M.Finding the position and orientation of a sensor on a robot manipulator using quaternions[J].International Journal of Robotics Research,1991,10(3):240-254. [3] Li A,Wang L,Wu D.Simultaneous robot-world and hand-eye calibration using dual-quaternions and Kronecker product[J].Inter J Phys Sci,2010,5(10):1530-1536. [4] 王君臣,王田苗,杨 艳,等.非线性最优机器人手眼标定[J].西安交通大学学报,2011(9):15-20. [5] Shah Mili.Solving the robot-world/hand-eye calibration problem using the kronecker product[J].Journal of Mechanisms and Robotics,2013,5(3):031007. [6] 戚 芳,席 锋.简便高精度的机器人手眼视觉标定方法[J].传感器与微系统,2006,25(1):27-29. [7] Heller J,Henrion D,Pajdla T.Hand-eye and robot-world calibration by global polynomial optimization[C]∥2014 IEEE International Conference on Robotics and Automation(ICRA),IEEE,2014:3157-3164. [8] Ruland T,Pajdla T,Kruger L.Globally optimal hand-eye calibration[C]∥2012 IEEE Conference on Computer Vision and Pattern Recognition(CVPR),IEEE,2012:1035-1042. [9] Ma Songde.A self-calibration technique for active vision system-s[J].IEEE Transactions on Robotics and Automation,1996,12(1):114-120. [10] Schmidt J,Niemann Heinrich.Data selection for hand-eye calibration:A vector quantization approach[J].International Journal of Robotic Res,2008,27(9):1027-1053. [11] Shi F H,Wang J H,Liu Y C.An approach to improve online hand-eye calibration[J].Lecture Notes in Computer Science,2005,3522:647-655. [12] 邹劲松,黄凯锋.一种新的三维测量机器人手眼标定方法[J].计算机测量与控制,2015(7):2270-2273. Research on precision influence factors based on hand-eye calibration equationsAX=XB* SHANG Zhong-yi1, DONG Ming-li1, LI Wei-xian1, LI Wei2 (1.Beijing Key Laboratory for Optoelectronic Measurement Technology,Beijing Information Science and Technology University,Beijing 100192,China; 2.Institute of Information Photonics and Optical Comunication,Beijing University of Posts and Telecommunications,Beijing 100876,China ) Hand pose data of robot affect hand-eye calibration precision can not be ignored.Influence factor based on hand-eye calibration equationAX=XBwhich affect on precision is analyzed.Calibration simulation and real experiments verify that influence of the above two factors on eye-hand calibration precision is consistent with theoretical analysis.Through simulation and actual experiments,the results are summarized that reducing distance between camera and target, reducing the difference between distance between the front and rear movement of the hand to the base coordinate space distances of robot,can improve hand-eye calibration precision,and by quaternion and matrix direct product method,verify that this rule of law in the solutionAX=XBuniversal calibration equations, when distance between camera and target is about 230 mm and distance from movement of robot hand to based coordinate space is 3.240 1 mm,precision of relative error of hand-eye calibration translation vector is up to 0.040 3 %. hand-eye calibration; robot; precision evaluation; calibration equation 10.13873/J.1000—9787(2017)03—0036—04 2016—04—15 国家重大科学仪器设备开发专项项目(2013YQ22089304);教育部“长江学者与创新团队”发展计划资助项目(IRT1212);北京市组织部青年骨干个人项目 TP 242 A 1000—9787(2017)03—0036—04 尚忠义(1988-),男,硕士研究生,主要研究方向为视觉精密测量。 董明利,女,通讯作者,教授,硕士生导师,主要从事视觉精密测量研究工作,E-mail:dongml@sina.com。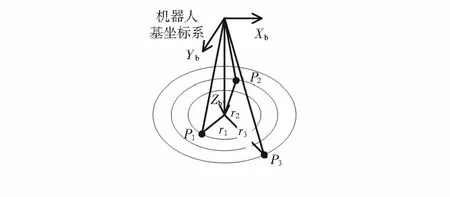




3 结 论

