LSFR算法在多传感器分布式检测中的优化研究*

刘 云, 陈昌凯， 崔自如

(昆明理工大学 信息工程与自动化学院， 云南 昆明 650500)

LSFR算法在多传感器分布式检测中的优化研究*

刘 云, 陈昌凯， 崔自如

(昆明理工大学 信息工程与自动化学院， 云南 昆明 650500)

在多传感器分布式检测系统中，常规融合规则算法要求传感器误差概率已知，且系统中传感器和融合中心同时优化存在一定困难。提出最小二乘融合规则(LSFR)算法，算法不依赖噪声环境稳定性以及传感器的虚警概率与检测概率，融合中心根据各个传感器的硬决策，得到全局的硬决策，并在传感器和融合中心处理达到最优时，获得最佳全局性能。仿真结果表明：对比似然比融合决策算法与Neyman Pearson融合规则(NPFR)算法，LSFR算法全局检测概率显著提高，且在不同数量规模传感器和更多类型的分布式检测系统中具有较好兼容性。

最小二乘融合规则算法； 多传感器； 分布式检测

0 引 言

在多传感器系统中，分布式的各个传感器检测同一目标，并且发送本地的硬决策到数据融合中心，融合中心通过处理得到全局决策[1]。通过改善多传感器系统性能，使之更加抗噪声干扰和电磁波干扰。

Zhang Hongting等人提出了似然比检验，每个独立传感器根据各自检测概率进行权衡，融合中心与门限进行比较达到全局的最佳检测概率[2]。在先验概率已知的情况下，各个传感器可通过似然比检验获得本地决策，可以导出似然比融合决策算法[2]。Zhang Q等人考虑由于功率或者带宽限制，每个传感器量化各自本地决策的二元信息至融合中心，给定全局虚警概率，全局检测概率达到全局最佳[3]。若先验概率未知，在本地传感器与融合中心，通过Neyman Pearson(NP)检测可以导出NP融合规则(NP fusion rule,NPFR)算法[3]。给定全局虚警概率，需最佳全局检测概率以获得最优融合算法，最佳全局检测概率只要在融合中心级别最优，就会造成系统性能降低[4]。文献[5]提出拟凸性，表明在融合中心级别有最优解，但在融合中心和传感器级别并没有同时达到全局最优[6]。

统计独立决策的NP融合优化，要求已知各个传感器的虚警概率与检测概率[7～9]。假定严格平稳的噪声环境，传感器的虚警概率与检测概率未知，融合算法将无法实现[10～12]。此外，由于环境噪声的波动与传感器阀值的不稳定性，也造成系统性能显著降低[13～15]。

本文提出了一种非参数化的硬决策的最小二乘融合规则(LSFR)算法，在传感器的虚警概率与检测概率未知、非严格平稳的噪声环境情况下，LSFR算法结合各个传感器的本地决策，得到全局决策，LSFR算法表现出较好的鲁棒性。

1 综合多参数的参考模型

假设有n个传感器节点，缺席目标为H0，存在目标为H1，且独立统计观测为x1,x2,…,xn，概率分布为p(xi|H0)，p(xi|H1)，i=1,2,…,xn。传感器i量化本地观测xi得到一个本地决策si，在二元决策中，传感器决策si取值0或1。融合中心处理本地决策{si}以获得全局决策s0。传感器的观测是统计独立，则{si}也为统计独立[3]。

在分布式检测系统中二元检测优化算法，根据NP准则，保持全局虚警概率PF低于给的定值，可得最佳全局检测概率PD[4]。其中PF=P(s0=1|H0)，PD=P(s0=1|H1)。

传感器对观测信息进行量化，得到本地二元决策

(1)

式中λi为传感器阈值，由第i只传感器虚警概率决定；Ti(xi)=p(xi|H1)/p(xi|H0)为第i只传感器的似然比检验。

融合中心的优化决策算法[4]可表示为

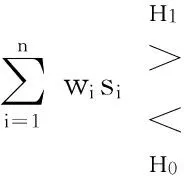
(2)

式中 λ0为融合中心的全局阈值，由融合中心的全局虚警概率PF决定；系数{wi}由第i个传感器的虚警概率PFi与检测概率pdi决定

(3)

pfi=p(si=1|H0),pdi=p(si=1|H1)，

i=1,2,…,n

(4)

从式(3)可知，最优融合算法需要已知每只传感器的虚警概率与检测概率，以及严格平稳的噪声环境。

根据NP准则，优化传感器和融合中心的结构，s表示传感器决策(s1,s2,…,sn)的向量，对于独立假设，则

(5)

融合中心的似然比检验[3]可表示为

(6)

在融合中心，全局虚警概率为

(7)

全局检测概率为

(8)

根据NP准则，最优融合决策[5]为

(9)

第i只传感器的最优融合决策为

(10)

i=1,2,…,n，j=0,1

(11)

式中s-i为s除去第i只传感器决策的向量。式(10)中的最优决策必须依赖于{Lij}，则须先求解式(9)的D(s)。另一方面，式(9)中的最优融合决策依赖于传感器阈值。综上所述，可得出由于传感器全局最优条件不是很明确，很难达到传感器全局最优。

2 LSFR算法

假设融合中心接收n只传感器决策si，i=1,2,…,n，经过数据融合，得到全局决策s0。向量s表示传感器的硬决策，即s=[s1,s2,…,sn]。假设:H0∶s=sc+N0，H1∶s=sc+N1。其中,sc为一向量，其各个元素为正确决策，N表示随机决策误差向量,则

Hθc∶s=sc+Nθc,θc=0,1

(12)

式中θc为正确决策，Nθc为随机决策误差向量，其元素值为0或1-2θc。

U为(n×1)列元素和为1的系数矩阵，θ值为0或1，F表示(n×1)列元素为1的矩阵，即

(13)

(14)

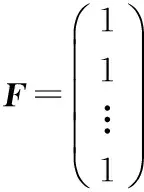
(15)

融合方程系统中

sU=θ

(16)

FTU=1

(17)

由式(12)、式(16)与式(17)可得

NθcU=θ-θc

(18)

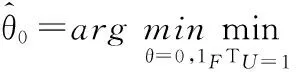
(19)

若s为零向量，融合中心的全局决策为H0；若s为元素全1的向量，融合中心的全局决策为H1。在这两种情况下，全局决策是正确的、独立的，但不符合实际情况。

定义下面的函数

f(U)=‖sU-θc‖2+γ(FTU-1)

(20)

式中γ为拉格朗日乘数。式(20)可写为

f(U)=UTsTsUT-UTsTθ-θTsU+θTθ+γ(FTU-1)

(21)

因为函数‖sU-θ‖2是凸函数，式(16)是线性的，那么式(21)为凸函数。对于变量U，最小化f(U)函数,则

(22)

由式(22)可得

U=(sTs)-1[sTθ-0.5γF]

(23)

式中 (sTs)-1为(sTs)的逆矩阵。如果式(22)为一常数，那么只有当

[In-(sTs)(sTs)-1](sTθ-0.5γ)=0

(24)

式中 In为序列n的特征向量。式(23)两边同时左乘FT，可得

FTU=FT(sTs)-1sTθ-0.5FTγF

(25)

因为F表示为n×1列元素全为1的向量，那么式(25)可以写为

FT(sTs)-1sTθ-0.5nγ=1

(26)

可导出

γ=(FT(sTs)-1sTθ-1)/(0.5n)

(27)

将式(27)代入到式(23)可得

U=(sTs)-1sTθ-([FT(sTs)-1sTθ-1]F/n)

(28)

由式(28)可知，若H0是正确的，则最优融合加权向量

U0=F/n

(29)

若H1是正确的，那么最优融合加权向量

U1=(sTs)-1sT-([FT(sTs)-1sT-1]F/n)

(30)

因为最优融合算法通过最小化f(U)函数可得，那么最优融合算法为

(31)

3 仿真分析

假定在瑞利分布下，n只传感器观测

p(xi|H0)=exp(-xi),xi≥0

(32)

p(xi|H1)=diexp(-di,-xi)

(33)

(34)

式中xi≥0，di>0,i=1,2,…,n，SNRi为第i只传感器的信噪比。

根据NP准则，融合中心融合算法为

(35)

根据NP准则二元决策融合，各传感器决策规则为

(36)

此外，本地传感器的检测概率与虚警概率关系[7]如下

(37)

图1可以看出:随信噪比的增加，似然比融合决策算法、NPFR算法与LSFR算法检测概率不断增加，LSFR算法的检测概率大于NPFR算法，NPFR算法的检测概率大于似然比融合决策算法。仿真结果表明，LSFR算法系统性能优于NPFR算法，NPFR算法系统性能优于似然比融合决策算法。

图1 在瑞利分布观测下不同传感器数n和不同虚警概率PF下的算法比较

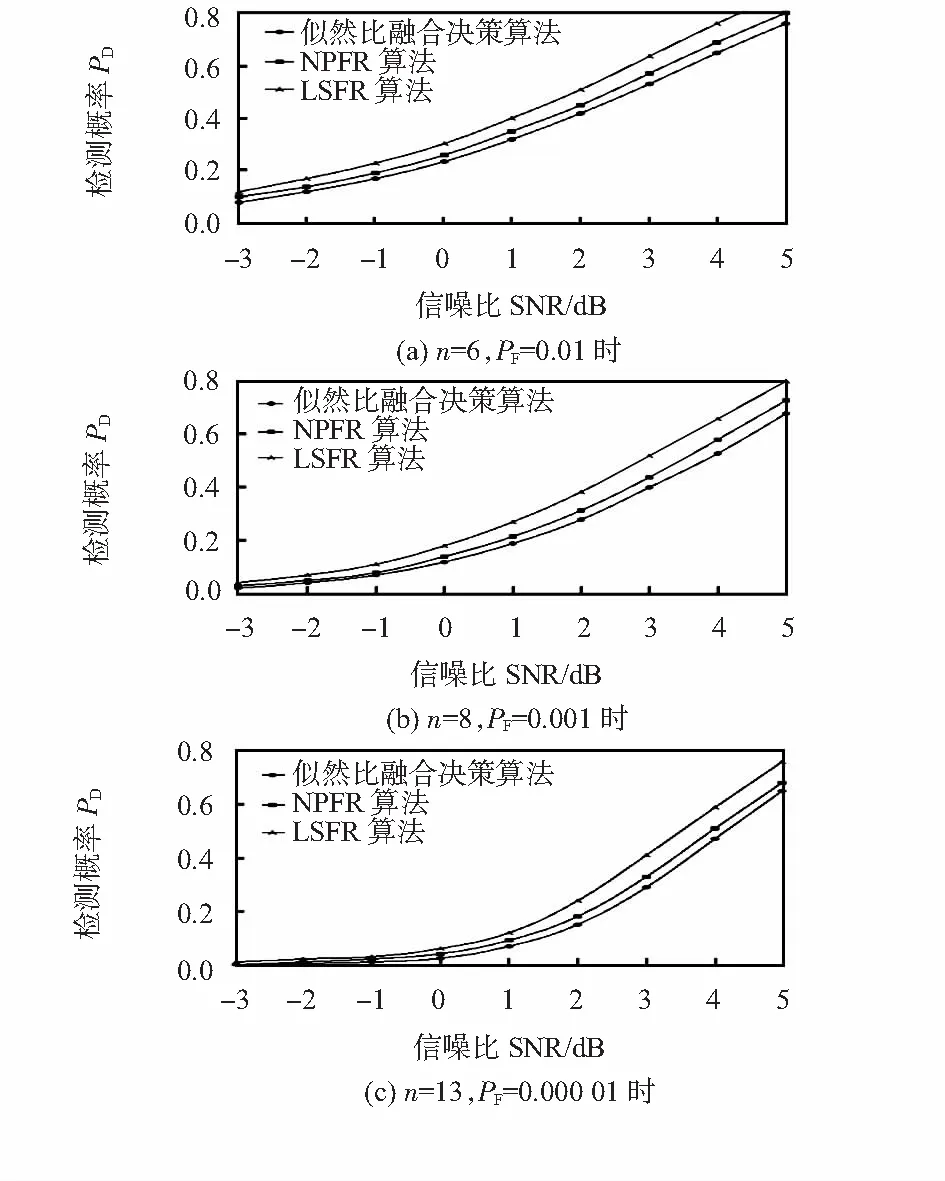
图2 在瑞利分布观测下不同传感器数n和较小虚警概率PF下的算法比较

图2可以看出:随信噪比的增加，似然比融合决策算法、NPFR算法与LSFR算法检测概率不断增加，LSFR算法的检测概率大于NPFR算法，NPFR算法的检测概率大于似然比融合决策算法。仿真结果表明，在较小的全局虚警概率情况下，LSFR算法可适用于任何传感器数量的分布式检测网络。

图1(a)和图2(a)可以看出，当传感器n=6以及虚警概率不同时，随着信噪比的增加，LSFR算法的检测概率大于NPFR算法，NPFR算法的检测概率大于似然比融合决策算法。虚警概率越大，LSFR算法、NPFR算法和似然比融合决策算法的检测概率收敛速度越快。

图1(b)和图2(b)可以看出，当传感器n=8以及虚警概率不同时，随着信噪比的增加，LSFR算法的检测概率大于NPFR算法，NPFR算法的检测概率大于似然比融合决策算法。虚警概率越大，LSFR算法、NPFR算法和似然比融合决策算法的检测概率收敛速度越快。图1和图2表明，在同数量传感器和同虚警概率情况下，LSFR算法都明显优于NPFR算法与似然比融合决策算法。

4 结 论

本文主要研究在多传感器分布式检测系统中数据融合问题，分析了算法需已知传感器误差概率。本文提出一种最小二乘融合算法，LSFR算法不要求已知误差概率，并获得较高检测概率。仿真结果表明：LSFR算法表现出良好的鲁棒性，以及在不同数量规模传感器和更多类型的分布式检测网络中具有较好兼容性。下一步工作将在数据融合方面自适应多传感器分布式检测系统深入研究。

[1] 张 晓,王 红.一种改进的基于大数据集的混合聚类算法[J].计算机工程与科学,2015,37(9)：1621-1626.

[2]ZhangHongting,WuHsiao-Chun,LuLu,Analysisandalgorithmforrobustadaptivecooperativespectrum-sensing[J].IEEETransactionsonWirelessCommunications,2014,13(2):618-629.

[3]ZhangQ,VarshneyP,WeselR.Optimalbi-levelquantizationofi.i.dsensorobservationsforbinaryhypothesistesting[J],IEEETransactionsonInformationTheory,2012,48(7):2105-2111.

[4]AshrafMAziz.Asoft-decisionfusionapproachformultiple-sensordistributedbinarydetectionsystems[J].IEEETransactionsonAerospaceandElectronicSystems,2011,47(3):2208-2216.

[5]ZoubirAM,KrishnamurthyVSayed.Signalprocessingtheoryandmethods[J].IEEESignalProcessingMagazine,2011,28(5):152-156.

[6]AldalahmehS,GhoghoM.Statisticalanalysisofoptimaldistributeddetectionfusionruleinwirelesssensornetworks[C]//IEEEConferencePublications,2012:49-53.

[7]LiuBin,JeremicA,WongKM.Optimaldistributedetectionofmultiplehypothesesusingblindalgorithm[J].IEEETransactionsonAerospaceandElectronicSystems,2011,47(1):317-331.

[8] 王海涛,刘 云.基于信任度的二次数据融合的研究[D].昆明:昆明理工大学,2013.

[9] 廖国琼,吴凌琴,万常选.基于概率衰减窗口模型的不确定数据流频繁模式挖掘[J].计算机研究与发展,2012,49(5)：1105-1115.

[10] 张步忠，程玉胜，王则林.基于片上多核的频繁项集并行挖掘算法[J].计算机科学，2014,41(3)：55-58.

[11]TangPeiyi,PetersonErichA.Miningprobabilisticfrequentcloseditemsetsinuncertaindatabases[C]∥The49thACMSoutheastConference,2011：24-26.

[12] 李如平，王 勇，徐珍玉.基于能量约束的多传感器故障非线性最优化规划决策机制[J].传感器与微系统,2014,33(11)：48-51.

[13]LiuBin,JeremicA,WongKM.Optimaldistributeddetectionofmultiplehypothesesusingblindalgorithm[J].IEEETransactionsonAerospaceandElectronicSystems,2011,47(1):317-331.

[14] 张 军，杨子晨.多传感器数据采集系统中的数据融合研究[J].传感器与微系统，2014,33(3):52-57.

[15]FerrariG,MartaloM.Decentralizeddetectioninclusteredsensornetworks[J].IEEETransactionsonAerospaceandElectronicSystems,2011,47(2): 959-973.

Optimization research on LSFR algorithm for distributed detection in multiple sensors systems*

LIU Yun, CHEN Chang-kai， CUI Zi-ru

(Faculty of Information Engineering and Automation,Kunming University of Science and Technology,Kunming 650500,China)

In multiple sensor distributed detection system, conventional fusion rule algorithm need to know the error probabilities of each sensor,and it is difficult to optimize the sensors and the fusion center simultaneously in the system.A least squares fusion rule(LSFR)algorithm is proposed,LSFR algorithm does not rely on any stability of the noise environment and false alarm and detection probabilities of the sensors.Fusion center combines the hard decisions of each sensor to make global hard decision,and acquire the optimal global performance when the processing of the sensors and fusion center are optimal.The simulation results show that,compare to likelihood ratio fusing decision-making algorithm and Neyman Pearson fusion rule(NPFR)algorithm,the global detection probability of LSFR algorithm is significantly improved,and LSFR algorithm has preferable compatibility in the distributed detection system of different scale of sensor and more types.

least square fusion rule(LSFR)algorithm; multiple sensors; distributed detection

10.13873/J.1000—9787(2017)03—0021—04

2016—04—08

国家自然科学基金资助项目(61262040)

TN 929.5

A

1000—9787(2017)03—0021—04

刘 云(1973-)男，副教授，主要从事无线通信研究工作。

陈昌凯，通讯作者，E-mail：663934451@qq.com。