太阳影子定位

姬安召，王玉风

(陇东学院能源工程学院，甘肃庆阳745000)

太阳影子定位

姬安召，王玉风

(陇东学院能源工程学院，甘肃庆阳745000)

太阳影子定位技术在视频数据分析中起着重要作用；采用天体运动中天球坐标系与地平坐标系之间的关系，建立杆影顶点的位置与杆高、太阳方位角与高度角的数学模型。根据视频拍摄的数据，以太阳方位角和高度角的方差之和最小为优化目标，将纬度、经度、时角和赤纬角视为变量。运用约束最优化算法进行求解，得出视频合理的拍摄时间和地点。

天球坐标系；地平坐标系；太阳高度角；太阳方位角；赤纬角；时角

太阳影子定位技术就是通过分析视频中物体的太阳影子变化，确定视频拍摄的地点和日期的一种方法，如何确定视频的拍摄地点和拍摄日期是视频数据分析的重要方面。本文研究是基于2015年全国大学生数学建模竞赛A题提供的材料。主要解决的问题：(1)建立影子长度变化的数学模型，分析影子长度关于各个参数的变化规律，并应用建立的模型画出2015年10月22日北京时间9∶00-15∶00之间天安门广场(北纬39度54分26秒，东经116度23分29秒)3米高的直杆的太阳影子长度的变化曲线。(2)根据某固定直杆在水平地面上的太阳影子顶点坐标数据，建立数学模型以确定直杆所处的地点。将所建立的模型应用于附件1的影子顶点坐标数据，给出若干个可能的地点。(3)根据某固定直杆在水平地面上的太阳影子顶点坐标数据，建立数学模型确定直杆所处的地点和日期。将建立的模型分别应用于附件2和附件3的影子顶点坐标数据，给出若干个可能的地点与日期。(4)附件4为一根直杆在太阳下的影子变化的视频，并且已通过某种方式估计出直杆的高度为2米。建立视频拍摄地点的数学模型，并给出若干个可能的拍摄地点。

1 假设和符号说明

1.1 模型假设

(1)忽略大气对太阳光的折射影响；

(2)太阳光线射入地球为平行光；

(3)在确定某一天，太阳的赤纬角不随时间(一天24小时之内)而变化；

(4)假设地球为圆球体。

1.2 符号说明

表1 公式符号说明

2 问题分析

通过问题分析和实际的观察可知，影子长度与太阳高度角、方位角、赤纬角、时角和杆长有关。地球自转并绕太阳公转，这个轨道线是固定的，日升日落。同一地点在一天内太阳高度角不断变化，而且一年四季每天的太阳高度角也是有变化的，但这个变化是固定的。若以地球作为参照物，地球是相对静止的，那么在地球上观察到的是太阳在天空中移动着。所以在一个规定的地方，每年同一天，太阳在此地上空运动轨迹我们认为是固定的，任何时刻的具体值都可求出。所以为了确切地描述太阳在天空中的移动轨迹与位置关系就应建立数学模型[1]。以地球球心O为中心，以任意长为半径作一假想球面，太阳这个球面上绕地轴转动，这个假想的球体称为天球[1]。延长地轴线与天球相交的两点称为天极，N′为北天极，S′为南天极，N′S′即为天轴。将地球赤道面无限放大与天球相交所成的圆PP′称为天球赤道。在无限放大的黄道平面上可以认为太阳沿着天球黄道绕地球周而复始地运动。

太阳在天球上的位置每日、每时都有变化。为了确定其位置，常用赤道坐标系和地平坐标系从不同角度来表示。

赤道坐标系[2]：是把地球上的经、纬度坐标系扩展至天球，在地球上与赤道面平行的纬度圈，在天球上则叫赤纬圈，在地球上通过南北极的经度圈，在天球上叫做时圈。以赤纬度(在南北回线之间变化)δ和时角Ω表示太阳的位置。

时角Ω：是指太阳所在的时圈与通过北点的时圈构成的夹角，单位为度。通过查阅文献[3]可知，时角Ω的计算方法为：

(1)

赤纬角δ：又称太阳赤纬，是地球赤道平面与太阳和地球中心的连线之间的夹角(见图2)。通过查阅文献[4]可得，赤纬角δ的计算方法为：

(2)

地平坐标系[5]：以地球表面上某一点的切面为基面建立空间直角坐标系，用太阳高度角hs和方位角As来确定太阳在天球中的位置(如图3所示)，从天球北极看，顺时针方向为正，逆时针方向为负。时角表示太阳在一天内的方位，因为天球在一天24h内旋转360度，所以每小时旋转15度。

图1 天球坐标系与地平坐标系的关系

太阳高度角hs：是指太阳直射光线与地平面间的夹角(见图1)，当太阳高度角为90度时，此时太阳辐射强度最大；当太阳斜射地面时，太阳辐射强度就小。通过查阅文献[6]可得，太阳高度角hs的计算方法为：

sin(hs)=sinδsinα+cosδcosαcosΩ

(3)

太阳方位角As：是指太阳直射光线在地平面上的投影线与地平面正北向所夹的角(见图1)，通常以北点S为0度(顺时针方向旋转，从0度到360度之间变化)。通过查阅文献[7]可知，太阳方位角As的计算方法为：

(4)

问题一：为了建立影子长度变化的数学模型，分析影子长度关于各个参数的变化规律。观测者是在地球地平面上对太阳的运动轨迹和影长进行观测，相对于观测者而言，地球是固定不动的，太阳围绕地球旋转。通过前面建立的天球坐标系和地平的坐标系关系，首先考虑太阳高度角与观测者所在地纬度、观测者观测日期的赤纬角和观测时间的时角的关系。太阳方位角观测者所在地纬度、观测者观测日期的赤纬角和观测时间的太阳高度角的关系；其次以观测者所在地的地平坐标系为参考系来描述太阳相对于该坐标系的运动规律，通过太阳高度角和太阳方位角来描述太阳相对于观测者的位置；再次以立杆与地平面的交点为坐标原点，地球经线在地平面的投影线为南北方向，北方向指向地球北极，地球纬线在地平面的投影线为东西方向。确定地平坐标系中立杆高度与太阳方位角和太阳高度角的几何投影关系，进而计算立杆顶点在地平坐标系中投影点随时间的变化关系；最后通过计算投影点的长度来描述影长与时间的变化关系。

问题二：结合问题一建立的数学模型，根据杆影顶点坐标数据反解出立杆所在地的经纬度。首先根据附件一已知的观测日期可以确定赤纬角，根据观测时间可以建立时角与经度的函数关系；然后由附件一观测的影子顶点坐标，结合问题一建立的模型，可以求出太阳方位角，再结合设定立杆的高度，可以求出太阳高度角；最后将上述结果代入问题一的模型即可求出可能的立杆所在地的经纬度。

问题三：结合问题二，设定立杆所在地的经度、纬度和赤纬角的变化范围，将上述数据代入问题一模型，可以计算出理论的影子顶点的位置数据，然后将计算出的结果与附件2和3的结果进行对比，求出两者之差的平方和最小为最优目标，当给定的纬度、经度和赤纬角满足上述条件时，即为立杆所在地的位置；最后根据赤纬角确定观测日期。

问题四：附件4中，由于在视屏中是2015年7月13日早晨九点左右拍摄的，由此可判断影子指向西方，根据影子移动变化方向，假设拍摄地在北半球，则影子在南北方向是向北移动的；假设拍摄地点在南半球，同样影子的方向为向西，而理论上影子应该偏南。对视屏中的杆影长度进行数据资料提取，得到杆影顶点坐标，然后代入问题二中的模型求解出位置。

3 模型的建立与求解

3.1 问题1模型建立及求解过程

以地平坐标系为基础，建立以立杆与地平面交点为坐标原点的杆影空间坐标系，y轴与地平坐标系的O′N轴(北极)平行，x轴与地平坐标系的O′E轴(东方向)平行，z′轴为与立杆重合，如图2所示。

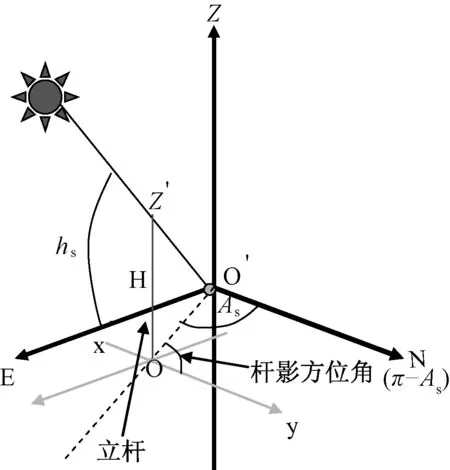
图2 太阳、杆影的位置关系图

根据上图的几何关系可得杆影顶点在xoy平面中的坐标：

(5)

将(1)～(4)代入(5)式可得杆影顶点的坐标，然后根据坐标计算出杆影的长度L。

(6)

表2 2015年各月份所对应的天数

将表2中的数据代入(6)式可得2015年10月22日的赤纬角为-12.1017度，纬度为0.6965rad。

将上述已知数据代入(6)式可得杆影长度与时间的关系曲线图，如图3所示。

图3 杆影长度与时间的关系曲线

由图3可得，从早晨9点到12点，杆影长度逐渐缩短，12点时杆影长度达到最小3.8411米，12点以后杆影长度逐渐变长。

3.2 问题2模型建立及求解过程

根据(5)式可得太阳方位角的表达式为：

(7)

由(7)式可知，只要已知杆影顶点坐标，就可求出太阳的方位角。注意：根据x和y值的正负关系判断方位角的大小。

具体确定方法如下：

(8)

根据(5)式可得太阳高度角的表达式为：

(9)

根据太阳方位角计算方法(4)式可得纬度计算公式：

cos(hs)cosδcos(As)=sinα-sin(hs)sinδ

(10)

当杆影位置和观测日期与时间已知时，通过求解(10)的非线性方程可得立杆所在地的纬度。具体求解方法如下：

令：

f(δ)=cos(hs)cosδcos(As)-[sinα-sin(hs)sinδ]

(11)

只要求解出(11)式的零点，即可求得纬度δ。

根据太阳高度角(3)式，将上述求解到的纬度δ、赤纬角和时角代入可得经度计算公式：

(12)

附件一的观测日期为2015年4月18日，根据表1中的数据代入(6)式可得2015年4月18日的赤纬角为10.511度。

将附件一数据代入(11)式求解可得可能的纬度为，结合(11)式求解的结果，根据(12)式计算可得可能的经度，具体计算的结果如下：

表3 杆影的位置

3.3 问题3模型建立及求解过程

在问题2模型的基础之上，将太阳赤纬角视为未知参数，日期是赤纬角的函数，通过设定立杆高度，根据给定纬度、经度和赤纬角的变化范围，通过(3)和(4)式计算可得太阳方位角和高度角；然后计算附件2和附件3中的已知数据，代入(8)和(9)可得已知杆影顶点数据的太阳方位角和高度角；最后通过两者之差的平方和最小为最优目标，求解附件2和附件3中可能的地点和日期。其具体模型如下：

(13)

根据(13)式模型的条件，编写MATLAB最优化程序，计算附件2、3得到结果如表4所示，附件2中的位置大约在北纬30.01529度，东经157.0815度。附件3中的位置大约在南纬27.0115度，东经98.04841度。

表4 杆影位置的求解结果

3.4 问题4的求解过程

附件4中杆高2米，拍摄日期和时间已知，直接将附件4中视频中采集的数据代入问题2计算可得立杆的拍摄位置，其具体计算结果如下表5所示。

表5 数据求解结果

附件4中的位置大约在南纬22.0127度，东经115.0567度。

4 模型结果分析

对于问题1：通过建立杆影长度与太阳高度角、方位角和杆高的关系，得到杆影长度随时间的变化关系，其基本规律符合观测结果，早晨太阳高度角较小，因此影较长，而中午太阳高度角较大，杆影长度较短，中午12点为最短。

对于问题2：通过问题建立的模型，反解立杆的位置，结合附件1算出不同杆高时所对应的位置，其具体变化规律为当观测日期及时间、影长不变时，杆高越长，其位置向北移动，而经度也略有变化。

对于问题3：相比问题2而言，问题3将观测日期视为未知参数，建立太阳方位角与计算太阳方位角之差平方和的关系，太阳高度角与计算太阳高度角之差平方和的关系，将二者的平方和之和的最小值作为目标，为给定区域寻求最优值，从而确定最佳的拟合位置和日期。附件2计算结果在北纬30.01529度，东经157.0815度，附件3计算结果大约在南纬27.0115度，东经98.04841度。

对于问题4：通过计算，附件4中确定位置的精度最高，方位角和高度角平方之和为0.13度。

5 模型评价

5.1 模型的优点

(1)模型中具有坚实可靠的数学基础，计算流程简单、方便、快捷、便于理解。

(2)模型应用广泛，在实际生活中具有实用性和代表性。

(3)模型中各个参数之间的关系表述明了、清晰。

5.2 模型的缺点

(1)没有考虑大气折射，忽略天气等自然因素的影响。

(2)没有把地球地轴运动考虑在内。

[1]王国安，米鸿涛，邓天宏，等.太阳高度角与日出日落时刻太阳方位角一年变化范围的计算[J].气象与环境科学，2007，9(30)：161-164.

[2]胡毅华，杨旭龙，刘媛萍.太阳影子定位模型的构建[J].洛阳师范学院学报，2015，11(34)：12-17.

[3]徐丰，王波，张海龙.建筑日照分析中太阳位置计算公式的改进研究[J].重庆建筑大学学报，2008，5(30)：130-134.

[4]陈晓勇，郑科科.对建筑日照计算中太阳赤纬角公式的探讨[J].浙江建筑，2011，9(28)：6-12.

[5]蒋洪力.太阳直射点纬度的数学推导和分析[J].数学通报，2007，9(46)：39-40.

[6]王建平.住宅单元日照环境的研究[J].建筑科学，2005，5(21)：31-36.

[7]朱丹丹，燕达.太阳能板放置最佳倾角研究[J].建筑科学，2012，1(28)：5-9.

【责任编辑 赵建萍】

The Location of the Sun’s Shadow

JI An-zhao, WANG Yu-feng

(SchoolofEnergyEngineering,LongDongUniversity,Qingyang745000,Gansu)

The sun shadow positioning technology plays an important role in the analysis of video data. Based on the relationship between the celestial coordinate and the horizontal coordinate during the motion of heavenly bodies, the mathematical model of the vertex position of the rod shadow and the height of the rod, as well as model of the sun’s azimuth and elevation angle is established. According to the data of video capture, and taking the minimum variance between the solar azimuth and altitude anglethe as optimization objective, the latitude, longitude, time angle and latitude angle are regarded as variables. The constrained optimization algorithm is used to solve the problem and to get a reasonable video shooting time and place.

errestrial coordinate system; horizontal coordinate system; solar altitude angle; solar azimuth; declination angle; hour angle

1674-1730(2017)01-0081-05

2016-03-24

姬安召(1983—)，男，甘肃庆城人，硕士，主要从事油气藏精细描述研究。

TE230

A