系统差及南纬站对GEO多站测距定轨精度的影响分析

高华宇，耿虎军，杜 兰，李 晶

(1.中国电子科技集团公司第五十四研究所，河北 石家庄 050081；2.解放军信息工程大学 导航与空天目标工程学院，河南 郑州 450002)

系统差及南纬站对GEO多站测距定轨精度的影响分析

高华宇1，耿虎军1，杜 兰2，李 晶1

(1.中国电子科技集团公司第五十四研究所，河北 石家庄 050081；2.解放军信息工程大学 导航与空天目标工程学院，河南 郑州 450002)

在基于多站测距的GEO卫星定轨中，为了提高卫星的定轨精度，通过仿真分析了测距系统差对定轨精度的影响。阐述了GEO卫星多站测距定轨的原理，分析了系统差的误差源及其修正精度，分析表明系统差综合修正误差在2 m左右；定轨仿真分析了系统差及南纬站对GEO卫星定轨精度的影响。实验结果表明，系统差主要影响GEO卫星切向和外法向定轨精度，南纬站的加入对改善外法向定轨精度作用显著。

GEO；定轨精度；系统差；多站测距；气象卫星

0 引言

地球静止轨道(GEO)是位于地球赤道上空固定高度约为36 000 km的轨道[1]。我国气象卫星有一定数量的GEO卫星，随着卫星研制技术的不断发展以及更多的业务需求，新一代气象卫星搭载了众多高精度有效载荷，这对GEO卫星精密定轨提出了更高的要求。

在多站测距体制中，观测数据所包含的测站系统差是影响定轨精度的主要因素之一[2]；更为重要的是，由于GEO的高轨静地特性，测量系统差难以通过定轨数据处理在线解算，更加依赖于外部校准。因此，测站系统差组合对GEO卫星定轨带来的影响将对工程应用具有指导意义。本文通过仿真分析了测距系统差对径向、切向和法向定轨精度的影响，并分析了南纬站对定轨精度的贡献。

1 多站测距定轨原理

多站测距定轨是通过多个地面测站对同一颗卫星进行双程测距，利用不同测站的观测弧段数据和卫星轨道动力学来确定卫星的运行轨道。

1.1 观测模型及其线性化

为简便起见，以单程测距观测量为例，其观测模型[3]可表达为：

Li(tj)=Gi(Xj,t)+Yi(tj)+ε。

(1)

式中，Gi(X,t)为t时刻测站i与GEO卫星的几何距离；Xj为GEO卫星tj时刻的运动状态；Yi(t)为t时刻各种系统差引起的等效测距误差之和；ε为随机误差。

对于某测站某确定时间段上的观测数据，定义

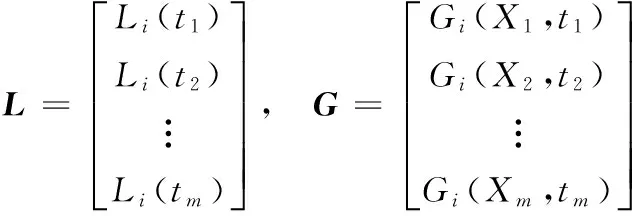
观测模型可表示为：

L=G+Y+ε。

(2)

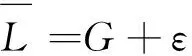
(3)

式(3)线性化后可得到线性化后的观测方程：

(4)

1.2 运动方程及其线性化

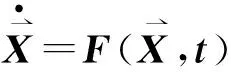
(5)

式中，

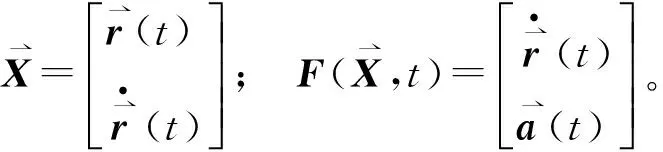
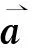
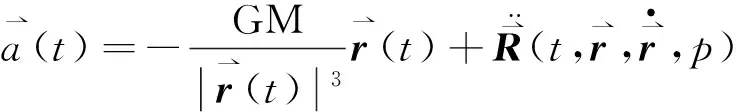
(6)

将式(5)在参考状态X*处进行泰勒展开，并略去高阶项可得线性化后的运动方程：

x(t)=Φ(t,t0)x(t0)。

(7)

式中，Φ(t,t0)为状态转移矩阵，可通过变分方程积分求得。

1.3 参数估计

由运动方程可知，卫星ti时刻的状态Xi可由初始t0时刻的状态X0进行积分得到，因此其函数关系可以表示为：

Xi=θi(X0,t0,ti)。

(8)

将式(8)代入式(4)可得观测方程[5-6]为：

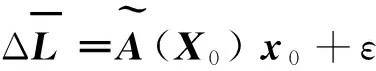
(9)

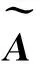
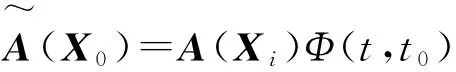
(10)

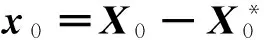
则观测残差可以表示为:

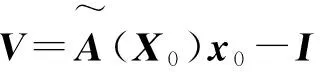
(11)

观测量权矩阵设为P，利用加权最小二乘法可得初值的最优改进量为：

(12)

解的协因数阵为:

(13)

2 系统差误差源及其改正量分析

系统差的误差源主要包括以下几类：与卫星有关的系统误差(如卫星钟差、卫星转发器延迟误差等)、与地面测站有关的系统误差(地面设备时延变化误差、站址偏差等)、对流层折射引起的等效距离误差和电离层引起的等效距离误差等[3]。

本文针对某GEO气象卫星，主要分析了以下误差源及其改正量，通过对误差源改正量求均方和得到了系统差估值，为后文仿真实验提供理论依据。

2.1 电离层延迟误差

电离层延迟误差是基于多站测距体制的GEO卫星定轨过程中较大的误差源，由此引起的误差最大时可达到150 m，最小时可达5 m[7-8]。常用的电离层修正方法有Klobuchar模型和双频改正法等，修正后电离层误差可达到1 m。

2.2 中性大气延迟误差

对流层延迟误差影响也是基于多站测距体制的GEO卫星定轨过程中主要误差源之一，主要是由对流层对电磁波的传播速度影响引起，对低仰角卫星，对流层总延迟最大可达30 m[9-10]，目前有Niell模型、Saastamoinen模型和Hopfield湿分量模型等，修正后对流层延迟误差优于0.5 m。

2.3 卫星转发器时延误差

卫星转发器在S频段的时延一般为几十米，但这是在地面测量获得的，发射到外太空，由于工作环境变为真空状态，并且受温度影响严重，卫星转发器零值与地面状态变化很大，通过修正，精度可达1 m。

2.4 地面设备时延变化误差

在相位调制测距系统中，由于温度、工作频率等因素影响[11]，调制信号会产生相位漂移误差，从而影响群时延特性，一般条件下一天时延的变化在1～2 m范围内，修正后精度优于1 m。

综上所述，不同误差源引起的系统差如表1所示。修正后的系统差均方和接近2 m。

表1 不同误差源误差结果

3 仿真实验

仿真时段为2016年6月13日0时至6时的多站测距观测数据，采样率为30 s，仿真的GEO卫星星下点经度为110.5°E，选择北京(B)、乌鲁木齐(W)、佳木斯(J)、广州(G)和墨尔本(M)5个测站对GEO卫星(S)进行跟踪观测，测站分布如图1所示。由于修正后的系统差均方和接近2 m，因此，测站系统差选择0.5 m、1 m、1.5 m和2 m四个量级进行测试，随机误差统一选择0.5 m，暂不考虑其他误差因素。

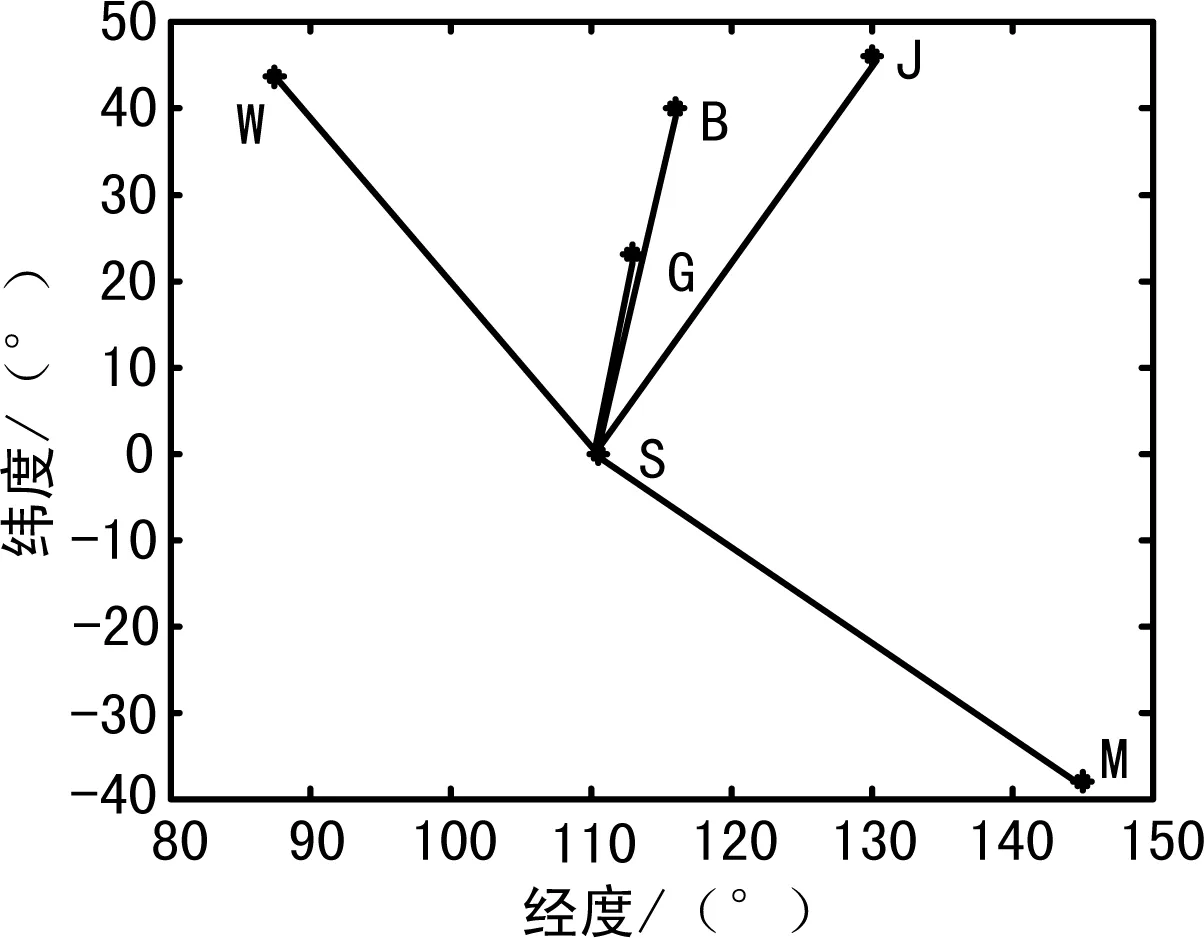
图1 测站分布

GEO卫星的摄动力考虑了30×30的地球非球形引力摄动、日月引力摄动、太阳光压摄动和潮汐引力摄动[12]。

3.1 仿真流程及定轨精度

首先，模拟一条真实轨道[13]作为参考轨道；然后，根据观测方程计算不同测站的双程几何距离，并加入系统差和随机误差作为观测数据；第三，使用多站的观测数据进行定轨，确定轨道精度。

定轨精度评定方法：在每个历元时刻，分别比较多站测距解算出的轨道和参考轨道在径向R、切向T和法向N的位置、速度误差Δi，计算不同历元时刻的均方根误差rmse作为定轨精度[14-15]，rmse值越小，定轨精度越高。

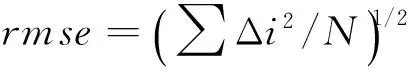
(14)

式中，Δi为i时刻解算轨道相对参考轨道的R/T/N分量误差，i=1,2,…,N。

为了客观评定仿真结果轨道精度，在确定一组测站系统差分配后，采用蒙特卡罗统计模拟方法仿真30次加入0.5m随机误差的观测数据，并进行定轨。对30次实验定轨结果做统计平均作为该组实验的结果。

3.2 仿真方案

在系统差设定中，令乌鲁木齐站和广州站系统差为-2m，佳木斯站和墨尔本站系统差为2m，所有测站的随机差均设置为0.5m。

方案1： 4个站测距定轨；去掉南纬站墨尔本站，设置北京站系统差分别为0.5m、1m、1.5m和2m四组实验，每组实验30次。

方案2： 5个站测距定轨。设置同上。

3.3 仿真结果分析

对每组实验中的30次重复实验进行统计平均后的定轨精度，分别给出了三维定轨精度和R、T、N方向的定轨精度，如表2所示。

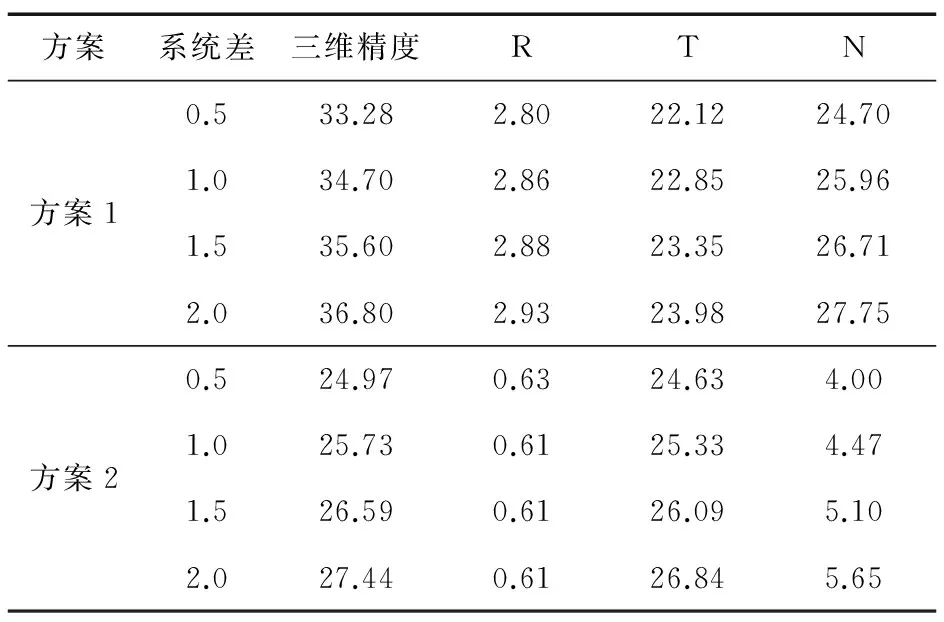
表2 平均定轨精度 (m)

2种方案中的8组实验统计平均后的定轨精度图如图2所示。图2中，4-0.5代表4个站定轨，北京站系统差为0.5 m时的定轨精度。

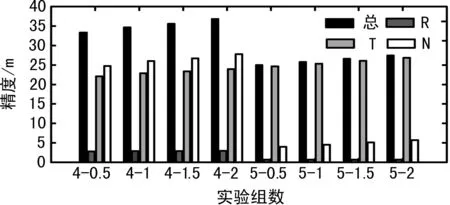
图2 每组实验平均定轨精度

从表2和图2可以看出，基于多站测距的GEO定轨误差受系统误差影响显著。

① 在没有南半球测站数据支持的情况下(见方案1)，其在径向上的影响与系统差本身量级相当，但是在切向和外法向上放大了10～40倍。

② 增加南半球测站对改进GEO外法向位置精度影响显著。与方案1相比，方案2由于南纬站墨尔本站的加入，外法向误差由近30 m减少到5 m左右，该方向位置分量精度提高近6倍。

③ 随着北京站系统差增加，整体定轨精度略有变差，但是浮动在米级。由于是仿真计算，不能完全反应真实数据条件下的各种复杂环境影响，因此，不断完善各类系统误差源的外部校正能力仍是十分必要的。

4 结束语

本文分析了5个站测距体制中测距系统差在2 m量级时，系统差对GEO卫星定轨精度的影响。仿真结果表明，测距系统差对定轨精度的影响主要表现在切向和法向上，而通过加入南纬站测距数据，可以很好地改进法向精度。但是本次研究完全基于仿真数据，不能完全反应真实数据条件下的各种复杂环境影响，需要不断完善系统差外部校正能力。同时，本次研究只是改进了法向精度，并没有改进切向精度，在后续实验中还会加入CEI观测数据来改进切向精度，利用测距和CEI观测数据联合定轨，提高GEO卫星定轨精度。

[1] 杜 兰，郑 勇，王 宏，等.GEO精密测定轨技术的现状及发展[J].飞行器测控学报，2005(6)：10-13.

[2] 杜 兰.GEO精密定轨技术研究[D].郑州：解放军信息工程大学，2006.

[3] 贺凯飞.顾及系统误差的GEO卫星定轨方法研究[D].西安：长安大学，2010.

[4] 刘伟平.导航卫星快速定轨和预报方法研究[D].郑州：中国人民解放军信息工程大学，2011.

[5] 王 威，于志坚.航天器轨道确定[M].北京：国防工业出版社，2007.

[6] 李济生.航天器轨道确定[M].北京：国防工业出版社，2003.

[7] 郝金明，吕志伟.卫星定位理论与方法[M].郑州：中国人民解放军信息工程大学，2012.

[8] 王文贯，唐诗华.GPS卫星定位误差概论[J].测绘与空间地理信息，2006(10)：39-42.

[9] 杨 杰,张 凡.高精度GPS差分定位技术比较研究[J].移动通信,2014,38(2):54-58+64.

[10] 沈洁莲,张 凡.CDMA网络辅助北斗定位时钟同步的可行性研究[J].移动通信,2015,39(5):71-74.

[11] 赵宏伟，刘 波，谢广钱，等.基于压缩感知的卫星干扰源定位[J].电讯技术，2015，55(5)：467-471.

[12] MONTENBRUCKOliver,GILL Eberhard.Satellite Orbits-Models,Methods and Applications[M].北京：国防工业出版社，2012.

[13] 智遂强.导航卫星实时定轨相关技术研究[D].郑州：中国人民解放军信息工程大学，2012.

[14] 李晓杰，杜 兰，黄金.CEI确定导航卫星轨道的精度分析[J].测绘信息与工程，2010，35(5)：14～15.

[15] 李晓杰.CEI在精密定轨中的应用研究[D].郑州：中国人民解放军信息工程大学，2009.

高华宇 男，(1990—)，硕士研究生。主要研究方向：航天测控、信号处理技术和航天器精密定轨。

耿虎军 男，(1971—)，硕士，研究员。主要研究方向：航天测控。

Influence of the Systematic Error on the GEO Determination Precision Based on Multi-station Ranging

GAO Hua-yu1,GENG Hu-jun1,DU Lan2，LI Jing1

(1.The54thResearchInstituteofCETC,ShijiazhuangHebei050081,China;2.InstituteofNavigation&Aerospace,InformationEngineeringUniversity,ZhengzhouHe’nan450002,China)

In order to improve GEO satellite orbit determination based on multi-station ranging,the influence of systematic differences on the precision of orbit determination is analyzed.Firstly,the principle of GEO satellite station ranging orbit determination is stated.Then the sources of the systematic error and their correction precision are analyzed.The results show that the systematic error valuation is in the order of 2 meters.Then the influence of the systematic error and south station on GEO satellite orbit determination is analyzed.The results show that the systematic error mainly influences the GEO satellite orbit determination precision in tangential and normal.Meanwhile,the addition of south station significantly improves the normal orbit determination precision.

GEO;precision of orbit determination;systematic differences;multi station ranging;meteorological satellite

10.3969/j.issn.1003-3106.2017.03.09

高华宇,耿虎军,杜 兰，等.系统差及南纬站对GEO多站测距定轨精度的影响分析[J].无线电工程,2017,47(3):35-38.

2016-12-20

国家高技术研究发展计划(“863”计划)基金资助项目(2013AA122105)；国家自然科学基金资助项目(41604011，61308061)。

P228

A

1003-3106(2017)03-0035-04