基于LBP特征和熵正则化Wasserstein距离的人脸表情识别

郑昌金 章登义 苏科华 武小平 洪 程

(武汉大学计算机学院 武汉 430072)

基于LBP特征和熵正则化Wasserstein距离的人脸表情识别

郑昌金 章登义 苏科华 武小平 洪 程

(武汉大学计算机学院 武汉 430072)

针对K最近邻分类中相似度量的量化问题,结合最优传输理论中Wasserstein距离数学特性,提出一种基于LBP特征和熵正则化Wasserstein距离的K近邻分类方法。首先对人脸表情图像进行预处理,然后使用LBP算子对图像进行特征提取获得LBP特征直方图,最后使用熵正则化的Wasserstein距离作为特征直方图之间的相似性度量的K最近邻分类方法进行人脸表情识别分类。实验结果表明该方法相较于单纯基于LBP的方法识别率有较大提高。

最优传输; Wasserstein距离; 人脸表情识别; 熵正则化; K最近邻分类

Class Number TP391.4

1 引言

人脸是人最重要的外貌特征,人脸表情是人类内在心里活动的外在反应,在人与人之间的情感表达和人际交往中起着非常重要的作用。基于面部表情的研究已经拥有一段很长的历史,20世纪70年代美国心理学家Ekman和Friesen[1]经过充分的实验,将人类表情定义为6种基本类型:开心、生气、难过、害怕、吃惊和厌恶,并指出这6种基本表情对不同种族具有普遍的适应性。心里学家Mehrabian[2]指出,人脸表情在人类日常交流中所传递的信息高达信息总量的55%。随着机器学习、数据挖掘和大数据时代的到来,基于人脸表情识别的数据挖掘和模式识别为人工智能的发展注入了新的活力,推动了人工智能领域研究的新一代浪潮。

人脸表情识别主要包含人脸检测、特征提取和特征分类三个方面的内容。图像识别所使用的特征提取主要分为几何特征和纹理特征。基于几何特征提取方法在提取人脸表情特征时一方面对人脸表情图像质量要求较高,另一方面忽略了脸部的纹理信息,在表情变化细微时识别率较低,因此本文采用基于纹理特征提取方法中比较常用的局部二值模式(LBP)特征。LBP算子由T.Ojala[3]提出,它是一种用来描述图像局部纹理特征的算子,具有计算简单、灰度不变性等优点,是通过比较周围像素点和中心点的大小来得到局部纹理特征的描述数据。2004年,T.Ahonen[4]首次在人脸识别中引入LBP。2006年,T.Ahonen在文献[5]中对LBP算法进行了改进。目前已经有许多基于LBP特征的人脸表情识别的研究,如蒋锐[6]提出基于多重中心化二值模式MLBP的人脸表情识别、齐兴[7]提出基于区域块LBP特征的人脸表情识别、叶棪[8]提出基于多尺度等价模式LBP的表情识别。

基于LBP特征表情识别主要采用K最近邻(KNN)[9]分类方法进行分类,但目前的研究大都是基于LBP特征的改进,对KNN分类方法中所使用的欧氏距离、曼哈顿距离等相似性度量存在的量化问题却少有研究,针对该问题并结合Wasserstein距离的数学特性,本文提出一种基于LBP特征和熵正则化Wasserstein距离的KNN人脸表情识别方法,使用Wasserstein距离可以很好地表征两个特征直方图之间的相似性。本文首先使用LBP算子对预处理之后的图像进行特征提取获得特征向量,然后结合最优传输理论中的Wasserstein距离和信息论中的熵,用熵正则化的Wasserstein距离作为图像之间相似性的度量进行K最近邻分类。

2 基本原理

2.1 局部二值模式(LBP)

原始的LBP算子定义在3*3的窗口内,以窗口中心像素为阈值,在给定的局部区域内的中心像素点像素值为gc,设以其为中心点的窗口近邻的8个点像素值分别为g1、g2、g3、g4、g5、g6、g7、g8,则3*3邻域内的8个点经比较可产生8位二进制数(通常转换为十进制数即LBP码,共256种),二值化比较处理过程中若满足gi>gc,i=1，…，8则置为1,反之就置为0,最后使用下列公式转化为十进制数值。

(1)

单个像素点的二值化处理如图1所示。

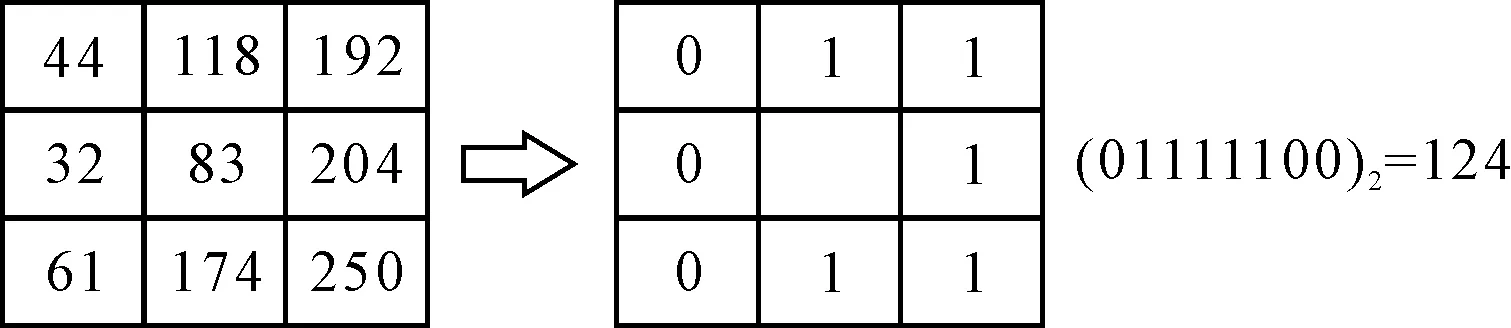
图1 单个像素点的LBP特征计算示例

2.2 最优传输理论和Wasserstein距离

最优传输问题已经有了一段很长的历史,最优传输问题的数学提法如下:给定欧氏空间中的区域U,V⊂R2,分配有概率密度u,v,总的测度相同满足:

∫Uu=∫Vv

(2)

考察一个微分同胚f:U→V,说这个映射是保测度的,对于任意一个集合B⊂V,其对应的原像满足:

∫f-1(B)u=∫Bv

(3)

称映射是保测度的,那么映射f:U→V的传输代价定义为

(4)

所有保测度映射中使得传输代价最小者就是最优传输映射。最优传输映射所计算的最小距离也就是Wasserstein距离。

人脸表情识别的最终任务就是通过某种准则来判断两种表情之间的相似性,而图像之间的相似性是以距离来反应的。从图像提取的LBP特征以特征统计直方图形式来表征,每幅图像的特征就组成一个特征向量。传统的距离度量从计算公式可以看出只考虑了两个空间向量之间的累积差异,却忽略了对应单个元素之间的差异。然而,特征向量每个位置的元素都代表一种LBP码的统计量,具有特定的意义。如特征直方图中第k个元素表示图像中LBP码取值为k的像素点的个数。从图像中所提取的特征向量因而就满足一个概率分布,而不仅仅是一个普通向量。使用传统的距离作为图像之间的相似性度量,将特征向量简单地当做普通向量处理,度量精度会存在较大的误差。因此,结合Wasserstein距离的数学特性,它对衡量不同概率分布之间的相似性具有很好的效果,因此本文采用最优传输理论中的Wasserstein距离来作为相似性度量。

在数学领域,Wasserstein距离作为一个距离的度量已经广泛地应用到概率论和数理统计中。它的数学定义如下:假设d(x,y)是一个度量,f(x)和g(x)是n维欧氏空间空间的概率分布函数。h(x,y)是联合分布函数,并且它的两个边际分布满足∫h(x,y)dx=g(y)和∫h(x,y)dy=f(x)。对于∀p>0,Wasserstein距离wp满足如下

(5)

min代表对于所有可能的h(x,y)所计算的距离取最小,p的一般取值为2。

2.3 熵正则化最优传输

最优传输中Wasserstein距离的原始计算办法是用线性规划求解,求解的核心就是找出所有联合分布中使得距离最小的方案。直接对所得特征向量进行相似度计算,计算复杂度会随着特征向量维度增加而变得非常复杂。为降低人脸表情识别中求解Wasserstein距离的时间复杂度,采用熵正则化约束的最优传输理论中通过在Wasserstein距离的基础之上增加熵项的方法[10～11],这种正则化具有许多优点,一方面将最优传输问题转化为一个严格凸问题,另一方面可以使用矩阵扩张算法中著名的Sinkhorn[12]不动点迭代来快速求解,理论证明可参考Cuturi[10]。根据信息论中熵的定义,为联合分布定义熵约束如下

H(h)=-∬h(x,y)lnh(x,y)dxdy

(6)

因此式(2)中的Wasserstein距离增加熵约束项之后可以定义熵正则化Wasserstein距离为如下形式:

(7)

当α>0,所要求解的h(x,y)是一个绝对连续的度量,否则,正则化熵项是不定的。通过增加-H(h)这一熵项约束让式(8)这个距离函数是严格凸函数,因此必定存在唯一的最优解。上述式子需要花费函数来表示从X到Y的运输花费,依据Cuturi的理论,运输花费函数的选择具有独立性。为方便计算定义核Kernel满足下式:

κ(x,y)=e-td(x,y)2

(8)

对于所有t>0,Kernel是正定的,将式(8)中定义的Kernel带入式(7)中,得到如下式(9):

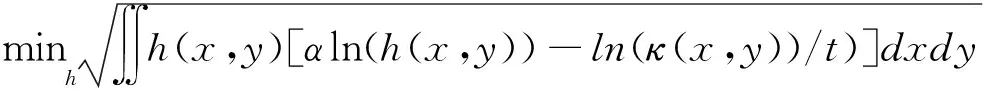
(9)

在实际求解过程中令t=1/α。

3 基于LBP特征和熵正则化Wasserstein距离的人脸表情识别

3.1 熵正则化Wasserstein距离的计算

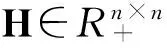
(10)

符号.*和./表示向量或矩阵之间对应元素的依次相乘和相除。

给定欧氏距离矩阵C依据式(8)得到正定矩阵K,Sinkhorn定理[13]表明存在唯一一个矩阵H满足如下的形式H=diag(p)Kdiag(q)并使得H∈P(M×M)。因此给定C和两个边际分布x和y,首先初始化两个m维(特征向量维度)的向量p和q,并由这两个向量构造出对角矩阵diag(p)和diag(q),然后使用矩阵扩张算法可以快速收敛,基于Sinkhorn不动点迭代的求解过程如下:

输入:两张人脸表情图像

输出:正则化Wasserstein距离d

1) 对输入的人脸表情图像进行预处理,提取局部LBP特征并得到特征向量;

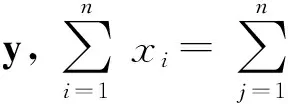
3) 初始化代价C为欧氏距离矩阵,初始化向量p和q为1;

4) //Sinkhorn迭代;

5) While(Δ(p)<ε){

6) p=x./K(a.*q);

7) q=y./KT(a.*p);

8) 计算Δ(p);

9) }//迭代向量p和q;

10) 使用式(10)计算d;

3.2 KNN人脸表情识别的步骤

人脸表情识别过程主要由三部分构成:图像预处理、特征提取、KNN图像识别分类。

1) 图像预处理

本文选择表情识别实验中常用的JAFFE[14]人脸表情数据库,该数据库中包含10位日本女性的生气、高兴、厌恶、惊讶、害怕、悲伤、中性7种表情,其中每人每种表情包含有3～4幅,考虑到JAFFE数据库表情原图中包含大量背景,因此首先选取一定数量的样本并选择脸部位置适中的地方进行统一的裁剪,图像的初始大小为256×256,裁剪之后大小为128×128,并把样本分为训练样本和测试样本两类。然后对所有样本采用高斯低通滤波来对图像进行平滑,过滤掉初始样本图像的部分噪点。裁剪之前的图像和裁剪后经过滤波处理的图像如图2所示。

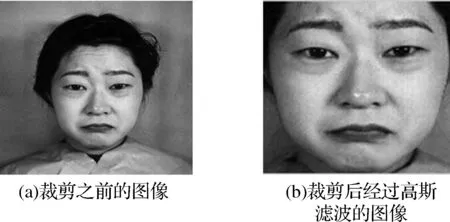
图2 裁剪前后图像

2) 特征提取

对预处理之后的所有样本进行特征提取,首先将一幅图像划分为互不相交的若干子区域如图3(a)所示,划分区块大小为32×32,然后对每一区域进行LBP特征提取,得到每个区域的LBP特征直方图,最后将每个区域的直方图归一化后组成特征向量,区域划分之后第一块和第二块的LBP特征直方图如图3(b)、3(c)所示。

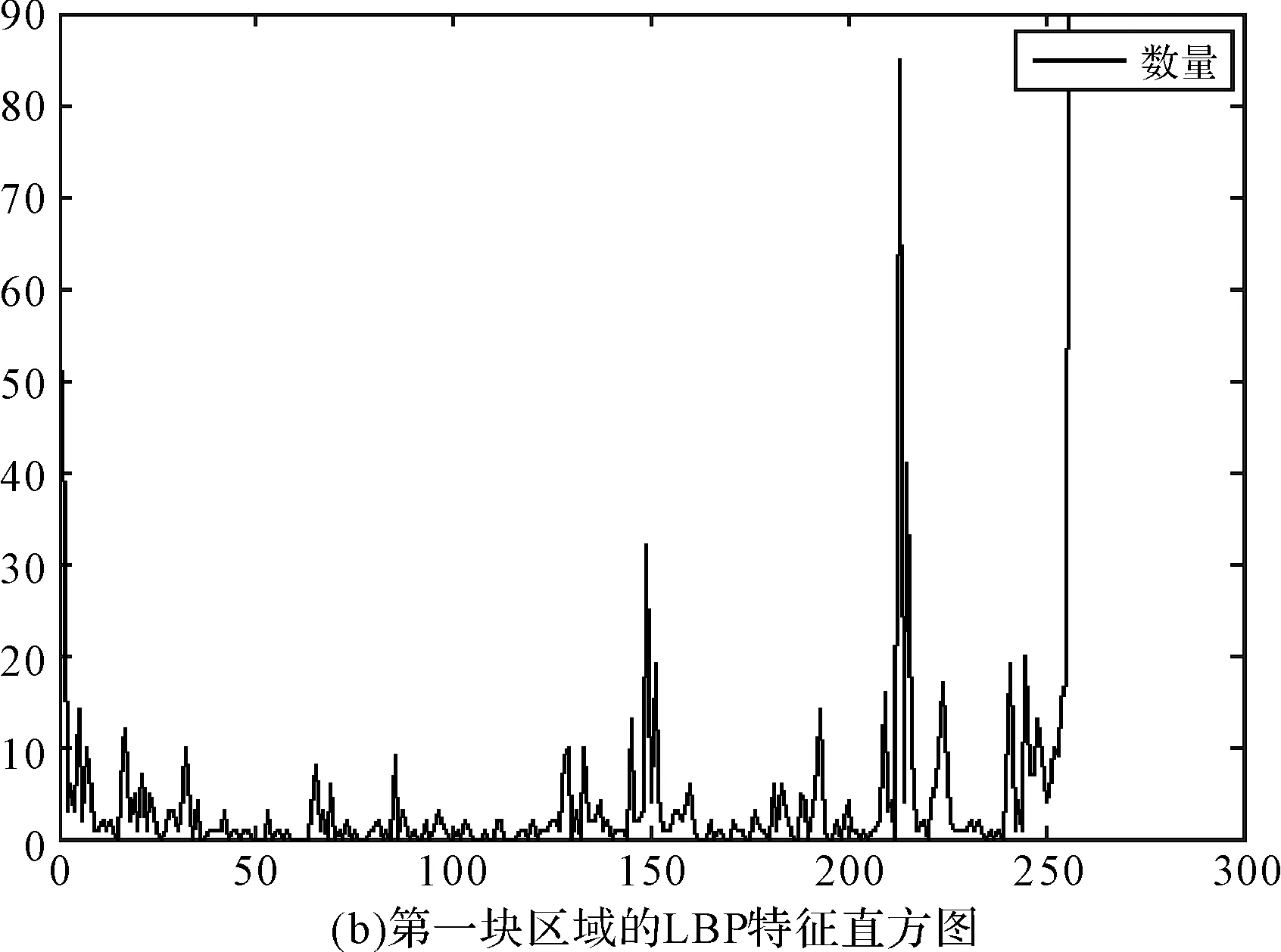
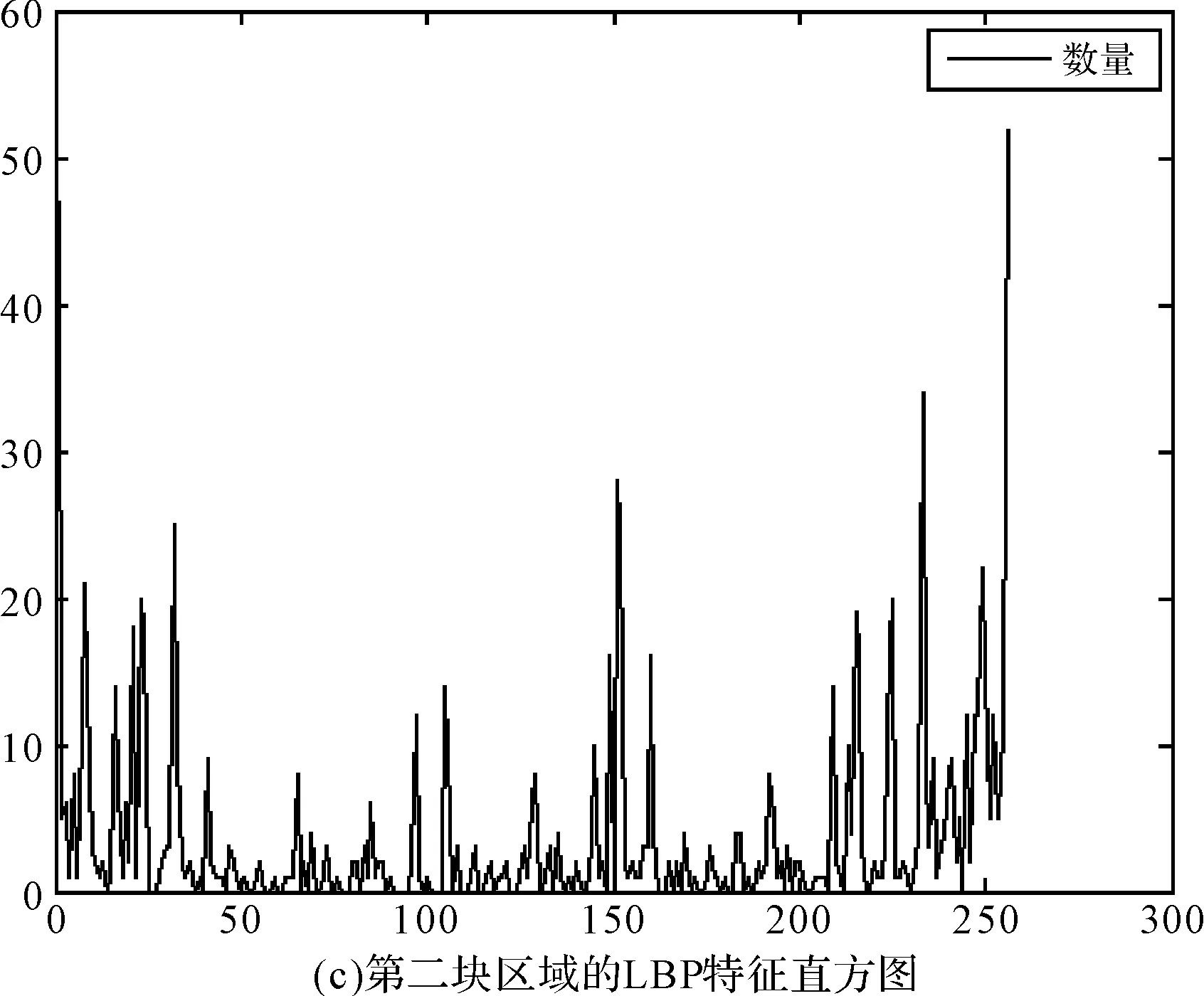
图3 特征直方图

3) KNN图像识别分类

以正则化的Wasserstein距离作为KNN分类中的相似度量,首先对训练样本中的不同表情赋予不同的标签,本文对六种表情分类,标签取值为1表示生气、2表示厌恶、3表示害怕、4表示高兴、5表示悲伤、6表示惊讶,然后计算每一个测试样本特征向量和训练样本特征向量之间的距离,依据所设定的K值记录距离每一个测试样本最近的K个训练样本中标签,最后将计数最多的标签值作为该测试样本所属的表情类别。

4 实验结果与分析

本文从JAFFE数据库中选择10位女性的前6种表情各3张共180张进行实验,其中每人每种表情2张共120张组成训练集,剩余每人每种表情各1张共60张作为测试集。

首先考察了KNN算法中K值对本文中的方法产生的影响,如下表1列出了K取不同值对准确率的影响,记平均识别率为c,每种测试表情的数量各10共60幅,每种表情实际识别数量为ri,i=1,2,3,4,5,6,则计算平均识别率如下:

(11)

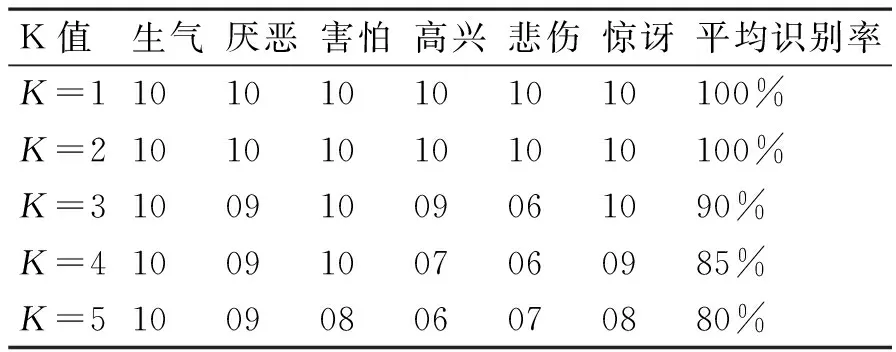
表1 5种K值下人脸表情识别率

通过实验结果可以表明K值的选择,对于分类结果的正确率存在一定的影响,当K值很小时,识别率很高但可能存在拟合,当K值变大时,虽然将更多的训练实例加入进行参考但是与此同时也会将与测试实例较远的训练实例加入增大了误差,因此选择适当大小的K值也至关重要。

接着选择表1中K值效果适中的值3并固定这个参数,对本文所采用的度量和KNN中常用的欧氏度量、角度距离、曼哈顿距离的效果进行对比,对比结果如表2所示。

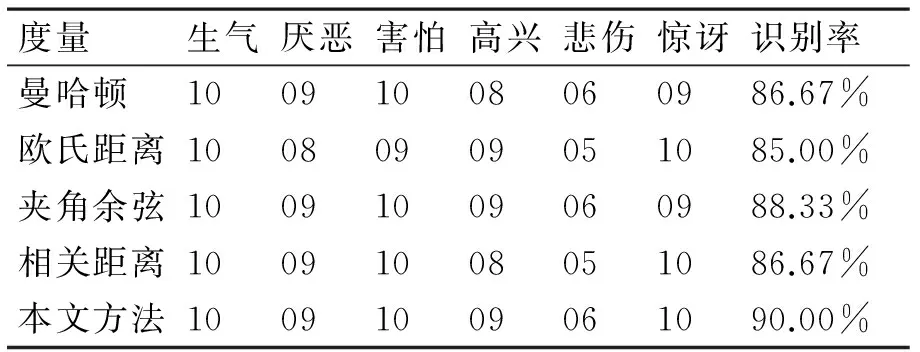
表2 5种距离度量人脸表情识别率

从表2中可以看出在固定参数K值之后,在保证相同的图像预处理,特征提取后特征向量相同的前提下,采用基于熵正则化Wasserstein距离的方法和其他几种距离度量相比较,具有更高的平均识别率,通过Wasserstein距离作为相似性度量提高了识别率,具有较好的效果。

最后就本文方法和文献[8]中方法进行对比,依次以120张样本中的每张表情作为测试样本,剩余的119张作为训练样本,最后按照不同的表情类别统计识别率,实验数据对比如图4所示。

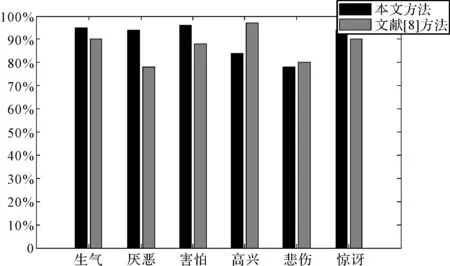
图4 本文方法和文献[8]方法对比图

从图中可以看出本文方法除高兴、悲伤以外其它表情的识别率都高于文献[8]中的方法。本文方法、文献[8]中的方法的平均识别率分别为92%、90%,从实验对比结果来看,本文方法平均识别率更高,从而说明使用Wasserstein距离相较于传统距离来作为满足一定概率分布的LBP特征直方图的相似度度量更加合适,验证了本文方法的有效性和可行性。

5 结语

本文结合最优传输理论研究的应用和其中最优方案度量Wasserstein距离的数学特性,并结合最优传输问题基于熵正则化最新求解方法,将熵正则化的Wasserstein距离作为图像之间的相似性度量应用到人脸表情识别中,使用最优传输的最小代价来表示不同特征分布之间的距离,避免了目前大多数度量中存在的量化问题,并通过实验结果证实了这种方法的有效性和可行性。

在以后的研究中,考虑将本文中的方法扩展到其它应用例如3D图像分类、图像插值、曲面图像识别和其他的工程领域。

[1] Ekman, P., Friesen, W. V. Facial Action Coding System. Palo Alto[M]. CA: Consulting Psychologists Press,1978.

[2] Mehrabian A, Russell J A. An approach to environmental psychology[M]. Cognition & Psychology,1974.

[3] Ojala T, Pietikäinen M, Mäenpää T. Multiresolution Gray-Scale and Rotation Invariant Texture Classification with Local Binary Patterns[J]. IEEE Transactions on Pattern Analysis & Machine Intelligence,2002,24(7):971-987,1-987.

[4] Ahonen T, Hadid A, Pietikäinen M. Face Recognition with Local Binary Patterns[J]. Lecture Notes in Computer Science,2004,3021:469-481.

[5] Ahonen T, Hadid A, Pietikäinen M. Face description with local binary patterns: application to face recognition[J]. IEEE Transactions on Pattern Analysis & Machine Intelligence,2006,28(12):2037-2041.

[6] 姜锐,许建龙,张爱朋.基于改进LBP的人脸表情识别[J].浙江理工大学学报,2013,30(4):546-549. JIANG Rui, XU Jianlong, ZHANG Aipeng. Facial expression recognition based on improved LBP feature[J]. Journal of Zhejiang Sci-tech University,2013,30(4):546-549.

[7] 齐兴,苏本跃.基于区域块LBP特征的人脸表情识别[J].安庆师范学院学报:自然科学版,2015,21(4):48-51. QI Xing, SU Benyue. Expression recognition based on block-area LBP features[J]. Journal of Anqing Normal University: Natural Sciences,2015,21(4):48-51.

[8] 叶棪,陈蕾,庞作超,等.基于多尺度等价模式LBP的人脸表情识别[J].计算机与数字工程,2016(1):40-44. YE Tan, CHEN Lei, CHANG Chao, et al. Facial expression recognition based on multi-scale LBP equivalent model[J]. Computer and Digital Engineering,2016(1):40-44.

[9] Short R D, Fukunaga K. A new nearest neighbor distance measure[C]//Proc. Fifth IEEE Int’l Conf. Pattern Recognition,1980:81-86.

[10] Cuturi M. Sinkhorn Distances: Lightspeed Computation of Optimal Transportation Distances[J]. Advances in Neural Information Processing Systems,2013,26:2292-2300.

[11] Solomon J, De Goes F, Peyr, Gabriel, et al. Convolutional wasserstein distances: efficient optimal transportation on geometric domains[J]. Acm Transactions on Graphics,2015,34(4):513-526.

[12] Sinkhorn R. A Relationship Between Arbitrary Positive Matrices and Doubly Stochastic Matrices[J]. Annals of Mathematical Statistics,1964,18(2):876-879.

[13] Sinkhorn R. Diagonal equivalence to matrices with perscribed row and column sums[J]. American Mathematical Monthly,1967,74(4):402-405.

[14] Lyons M, Akamatsu S, Kamachi M, et al. Coding facial expressions with Gabor wavelets[C]//IEEE International Conference on Automatic Face and Gesture Recognition, 1998. Proceedings,1998:200-205.

Facial Expression Recognition Based on LBP Features and Entropy-regularized Wasserstein Distance

ZHENG Changjin ZHANG Dengyi SU Kehua WU Xiaoping HONG Cheng

(School of Computer, Wuhan University, Wuhan 430072)

To solve quantification of similarity measure in the K-nearest neighbor classification, a KNN method is proposed based on LBP features and entropy-regularized Wasserstein distance, by combining the mathematical properties of Wasserstein distance in optimal mass transportation theory. Firstly, facial expression images are preprocessed. Secondly, LBP operator is applied to extract LBP feature histograms. Lastly, the K-nearest neighbor method with entropy-regularized Wasserstein distance as the similarity measure between feature histograms is used to recognize and classify facial expressions. Experimental results show that compared to the methods based on LBP only, the method greatly increases the recognition rate.

optimal mass trassportation, Wasserstein distance, human facial expression recognition, entropic regularization, K-nearnest neighbor classification

2016年8月5日,

2016年9月21日

湖北省科技支撑计划(编号:2014BAA149)资助。

郑昌金,男,硕士研究生,研究方向:计算机图形图像。章登义,男,硕士,教授,研究方向:计算机视觉。苏科华,男,博士,副教授,研究方向:计算机图形图像。武小平,男,博士,副教授,研究方向:计算机安防和实时监控。洪程,男,硕士研究生,研究方向:计算机图形图像。

TP391.4

10.3969/j.issn.1672-9722.2017.02.010