创设问题情境 激发学习兴趣
任晓燕
摘 要:所谓“问题情境”,是把学生置于研究新的、未知的学习氛围中,使学生在提出问题、思考问题、解决问题的动态过程中主动参与数学学习。这种学习活动不仅让学生将已有的知识灵活运用于实际,而且从这个学习过程中学生可以获得新的数学知识和方法。因此,在课堂教学中,创设各种情境不仅可以使学生在具体情境中理解和认识数学知识,体会数学知识的产生、形成与发展过程,还可以使学生获得积极的情感体验,感受数学的魅力,同时掌握必要的基础知识与基本技能。
关键词:问题情境;激发;兴趣
数学教学是解决数学问题的心智活动,让学生在具体的问题情境中获得对一类数学现象的规律性认识,并形成相应的数学模式,最后将模式广泛运用于同类问题情境中。因此,优化问题教学是激发学生学习兴趣和提高思维效率的关键。创设课堂问题情境应以吸引学生的注意力,激发学生的学习兴趣,与学生学习的知识能够产生直接或间接的关联为基础。根据小学生的心理与生理特点,创设优质的问题教学情境是调动学生心智活动积极性的重要途径。具体可从以下几个方面进行:
一、创设悬念性的问题情境
悬念设置的方法有很多,可以根据教学需要而定。若把悬念设置在课始,学生一上课,就有急于学习解决问题知识的需求,从而调动学生学习的积极性和主动性。若把悬念设置在课尾,具有“欲知后事如何,且听下回分解”的魅力,学生感到余味无穷,从而激发学生继续学习和思考的热情。
【案例一】(小学数学人教版第五册“正方形和长方形的周长”)
师:两只调皮的小蚂蚁决定比耐力,看谁爬得快?(师出示两边框)红蚂蚁沿着正方形边框爬一周,黑蚂蚁沿着长方形边框爬一周,看誰先回到起点。就在乌龟裁判宣布预备开始时,黑蚂蚁嚷开了:不公平,不公平,我爬的路比红蚂蚁的长,红蚂蚁也叫了:我爬的路比你的长才是呢!乌龟裁判是“丈二和尚摸不着头脑”,不知该如何?
师:小朋友们,你们认为呢?到底谁爬的路长?
(开始学生也不知怎么办,有同学猜一样长。)
生1:要知道两只蚂蚁爬的边框的长度各是多少,就可以比了。
师:根据刚才的观察,你能提出一个数学问题吗?
生1:求两只小蚂蚁各跑了多少路?
师:红蚂蚁和黑蚂蚁都沿着框爬了一周,从起点出发又回到这个起点,我们把这一周的长度叫做周长(板书:周长)。今天我们就来研究有趣的数学问题——周长。
创设问题情境的核心成分必须是新的、未知的内容,是为了学生正确掌握新的学习内容、基本技能及提高学生解决问题能力所精心设计的情境,把悬念设置在课始,学生一上课,就有急于学习解决问题知识的需求,把学生带入一种与问题有关的情境中去,进行有效的学习,从而调动学生学习的积极性和主动性。
【案例二】
年龄问题是小学数学较为复杂的应用题,学生对此问题非常感兴趣。如,在学生学习、掌握解决此类问题的一般方法后,课尾可提出这样的思考题:小花猫、大公鸡和山羊是好朋友,它们年龄虽然都不同,但爱好都很相似,正如它们对外夸口说的“忘年交”。一天,大象伯伯看到它们三个正在讲故事,便上前问道:“你们三个,究竟谁最大?谁最小?”山羊幽默地说:“我的年龄乘以■,公鸡的年龄乘以■,小花猫的年龄乘以■,这样算出来的三个年龄就一样大了。你能把我们三个按年龄的大小依次排列起来吗?”大象伯伯糊涂了,同学们,你们能在课后帮大象伯伯找出答案吗?对于这样的题目,学生兴趣盎然、乐此不疲地进行钻研。这一问题表面看“山重水复疑无路”很有难度,但学生一旦把握住“算出来的三个年龄就一样大了”这个关键,就会“柳暗花明又一村”,不难得出正确答案。
悬念可使学生的注意、记忆、思维高度集中,达到心智活动的最佳状态,有利于学生智力的开发,还能促进当前的学习。
二、创设生活性的问题情境
作为一个小学生,他们已有的知识很少,他们更多的是利用自己的生活经验来理解和接受新的数学知识。数学学习材料往往是比较抽象的,但在这抽象的背后我们总能找到它与生活的联系,因此,教师在创设情境时,先要对学生已有的生活经验和学习材料进行分析、比较,把握两者之间的联系,再来寻找一个合适的、有价值的、生活性的问题情境。如,在“人民币的简单计算”一课中,在学生掌握了元、角、分的换算后,用小数的方式表示商品的单价,如果直接告诉学生小数点的左边表示元,小数点右边第一位表示角,第二位表示分,学生接受起来可能会比较困难,那么创设一个在超市购物的情境,让学生根据已有的生活经验自己探索、交流,就变得不是难题了。
数学教学要密切地联系生活实际,贴近生活。如,我在教除法之前,向学生提了一个问题,让学生思考回答:当你家来了10个客人,你的妈妈让你做饭给他们吃,做的饭既不能不够,又不能有剩余,那该怎么做?有的说:问一问每个客人吃几碗饭,然后把所有的碗数加在一起得出总碗数;有的说:估计每人吃几两米,然后用10去乘每人吃的米的重量,得出总重量;有的说:按每两个人吃一碗米做的饭,看10个人里面有几个两人,就做几碗米的饭……最后,我出示例题,有120支铅笔,每40支装一盒,可以装几盒?让学生读后想,120支里有多少个40支,就可以装多少盒,学生很快就列出算式,解答出来了。
三、创设操作性的问题情境
教育家波莉亚说:“学习任何知识的最佳途径都是由自己去发现的。因为这种发现理解最深,也最容易掌握其中的规律、性质和联系。”而这种发现必须是通过学生动手操作、动眼观察、动脑思考获取的。所以在探求新知时,要为学生提供必要的思维材料,设置“动境”,使学生借助已有知识、技能,调动多种感官参与新知的主动探究。
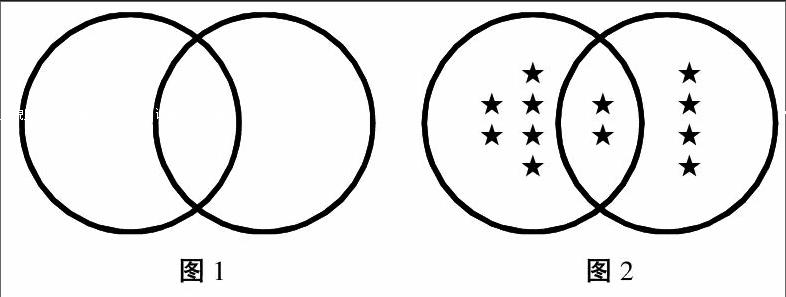
【案例三】(人教版三年级下册“重叠问题”)
师:拿出2个大的呼啦圈(一个红色、一个绿色),摆在地上(两圈相距约2米)。请第二小组(12人)喜欢打乒乓球的同学站到红色圈里,喜欢跳皮筋的同学站到绿色圈里。
生:喜欢打乒乓球的8人中,有6人站到红色圈里;喜欢跳皮筋的6人中,有4人站到绿色圈里,剩下2个同学先站到红色圈中,觉得不妥,又站到绿色圈中,依然感觉不妥,有些无所适从。感觉站到哪个圈似乎都不合适,有些迷茫地望着老师。
师:(看着一脸迷茫的同学)圈外边的两个同学该怎么站?
生:(看着两个离开的呼啦圈思考着。)
师:(静静的,没有过多提示语,只是微笑地看着认真思考的同学。)
生:一女生要求两个圈里的同学都出来,她把两个呼啦圈拉在一起,中间稍微重叠了一部分,摆成两圆相交状态(图1)
生:游戏继续,第2组同学根据自己喜欢的项目站成如上状态(图2)。
师:请同学们仔细观察,两个圈中间这一部分是喜欢什么项目的同学?你能用语文里的“既……又……”来说一说吗?
生:两个圈中间重叠部分是既喜欢打乒乓球又喜欢跳皮筋的同学。
师:第2组一共有多少名同学?
生1:6+2+4=12(人),
6表示只喜欢打乒乓球的同学,4表示只喜歡跳皮筋的同学,2表示既喜欢打乒乓球又喜欢跳皮筋的同学,一共有12人。
生2:8+6-2=12(人)
8表示喜欢打乒乓球的同学,6表示喜欢跳皮筋的同学,中间重复的2个人多算了1次,所以要减去一个2。
生3:8+4=12(人)
用红色呼啦圈里的人数8,加上右边绿色月亮里的人数4,等于两个呼啦圈里的人数之和。
生4:6+6=12(人)
用绿色呼啦圈里的人数6,加上左边红色月亮里的人数6,等于两个呼啦圈里的人数之和。
看似简单的游戏,其实里面“暗藏玄机”。创设这样一个“动境”,把思考的空间留给了学生,使学生在操作过程中,通过动眼观察、动手摆拼、动脑思维的自主探究获取新知识。同时,学生的创造性思维也得到了锻炼。
四、创设层次性的问题情境
问题应包含丰富的内涵,以点带面,逐渐扩展和深入,通过对一个问题的探究,全面触及知识的纵横,使学生从一个问题的解决中,有层次地掌握知识和技能,使课堂教学内容大大紧缩,促进课堂效率的提高。同时,针对不同层次的学生设计不同层次的问题,使每个学生都能获得学习的乐趣。
【案例四】(倍的认识)
教学“倍的认识”,在揭示了倍的概念后,设计这样一个问题情境:同学们布置教室开联欢会,按下图的顺序挂气球:
蓝 黄 黄 红 红 红 红 蓝 黄 黄 红 红 红 红
并分成这样几个问题层次:
第一层:黄色气球个数是蓝色气球个数的多少倍?红色气球个数是蓝色气球个数的多少倍?红色气球个数是黄色气球个数的多少倍?
第二层:同学们已经买来6个黄色气球,还应买来多少个蓝色气球和多少个红色气球?
第三层:同学们已经按上图的顺序蓝、黄、红三色气球买来37个,蓝、黄、红色气球各有几个?
三个不同层次的问题针对不同的学生,使后进生“吃得了”,中等生“吃得饱”,优生“吃得好”,促进学生的全面发展。
教学实践和研究都表明,从学生的年龄特征和心理状态着手,创设“悬念”“活动”“趣味”等教学情境,符合课改的要求,能“促进学生在教师的指导下主动地、富有个性地学习”(《纲要》语),还能有效地激起学生旺盛的求知欲,调动学生的学习积极性,增强他们学习数学的兴趣和毅力。
数学教学过程中教师要不断地创设问题情境,使学生有“一波未平,一波又起”之感,将学生引入“不平衡—探究发现—问题解决—平衡”的探究过程,让学生自始至终积极主动地参与数学的课堂学习。
问题情境创设的方法非常多,但如何来创设一个合适的、有价值的,能够让学生获取知识,促进学生发展和获得情感体验的问题情境,还需我们一线的教师在实践中不断地去分析、反思和探讨。

