综合平均曲率与网格边的特征线提取方法

王钦瑞 张应中 罗晓芳

(大连理工大学机械工程学院 辽宁 大连 116024)

综合平均曲率与网格边的特征线提取方法

王钦瑞 张应中 罗晓芳

(大连理工大学机械工程学院 辽宁 大连 116024)

随着数字几何获取技术的发展，大量的复杂形体采用网格模型表示。而网格模型的特征线或特征边缘的识别和提取是后续开展几何和特征识别的基础工作，为此提出一种综合平均曲率与网格边的三角网格模型特征线提取方法。分两次提取：首先利用三角面片法矢夹角大小对模型中的尖锐边进行初次提取特征点；然后综合平均曲率与网格边的关系对特征点进行二次提取；最后用两次提取边的顶点作为特征点，进行分类分组处理拟合成特征线。经过实例验证，该算法可以快速地提取尖锐边和过渡边等，具有很好的提取效果。

特征线提取 三角网格模型 曲率估计 逆向工程

0 引 言

随着数字几何获取技术的发展，大量的复杂形体采用三角网格表示。三角网格可以表达任意形状和拓扑的三维几何模型，但是对采样获取的三角网格模型还需要开展很多后续几何处理工作，例如几何特征提取、网格分割以及模型重构等。网格模型的特征线或特征边缘的识别和提取是后续几何和特征识别的基础。经过多年的发展，很多学者对如何从三角网格模型中提取特征线的问题提出了很多方法，主要分为两大类，即基于面和基于边的方法。此外还有一些学者将两种方法结合起来，如Razdan等[1]。

基于面的方法主要是对三角网格数据模型中的点根据某种属性(例如法矢、主曲率以及特征值等) 进行标识。然后选取一组“种子点”，从这些“种子点”开始进行K-阶邻域的区域增长，找出具有相同标识的点归为同一数据块，直到K-阶邻域没有与标识一样的点才停止区域增长。整个网格数据模型的点都被划分为不同数据块，而不同数据块之间的边界就构成了网格模型的特征线。例如，Wang等[2]先根据曲率将顶点分类，再利用统计学方法和高斯映射进行区域增长，从而确定模型的特征线；韩丽等[3]的基于离散曲率的网格分割方法，采用曲率作为点的标识，进行区域增长；Kim等[4]的基于张量投票理论的特征线提取方法，采用张量投票矩阵特征值作为点的标识，依据特征值分布与点的几何特征之间关系对顶点进行分类，张慧娟等[5]对其方法进行了优化处理。这种方法对二次曲面效果较好，对自由曲面则效果不佳。

基于边的三角网格数据模型特征线提取的方法一般先对网格离散顶点进行曲率估计，找出那些曲率突变点，并将其作为特征点，最后将这些特征点有序地拟合成线，即特征线。典型的有Milroy等[6]在OCS(Orthogonal Cross Section) 模型上，估算三角网格模型上各点的法矢，利用法矢和K-阶邻域的点的信息拟合成一张二次曲面，从而计算出主曲率与主方向。若主曲率在主方向上取得极值，则该点被确定为特征点，然后利用能量最小化原则将特征点连接成线，即为特征线。刘胜兰等[7]根据一条边上两个相邻三角面片法矢的夹角和每个顶点的主曲率是否在主方向上为极值，分两次提取，再将这些点连成线。这些方法对特征点的判断计算量大，降低了提取效率。

本文在深入分析以前算法的基础上提出一种新的对三角网格模型中的特征线提取算法。该算法是在三角网格数据模型的基础上采用综合平均曲率与网格边的方法来实现的，省略了对特征点的直接判断，而是通过网格模型三角形边是否为特征边间接地判断该特征边的两个端点是否为特征点，提高了效率。

1 Taubin曲率估计算法分析及改进

曲率估计算法一般分为两大类算法：一是K-阶邻域曲面拟合法[8]，二是顶点离散估计[9]。K-阶邻域曲面拟合法是将一点与周围K-阶邻域顶点进行局部拟合成一个曲面，利用拟合曲面的方程计算该点的曲率。K值越大，拟合区域越大，估算曲率也就越精确，抗噪性越好，但计算量就会越大。顶点离散估计法相对于拟合法减少了计算量，提高了估算效率。Taubin利用特征向量方法估算了顶点主曲率与主方向，该方法在网格分布均匀时因估算准确，计算量小而得到广泛使用。

1.1 网格顶点法矢估计

Taubin曲率估计算法[9]首先是对顶点法矢的估算，顶点法矢的估算尤为重要，直接影响后面对称矩阵的构造以及曲率的精确度。在三角网格拓扑重建过程中保存了点、线、面的邻接关系以及面的法矢，从图1可以看出，点vi的一环邻域中的点、线、面的关系。Taubin顶点法矢是以面积为权值的相邻三角面片的法矢的矢量和，具体估算为：

(1)

其中，fk为三角面片的面积，Fi为顶点相邻的所有三角形，Nfk为三角面片的法矢量。

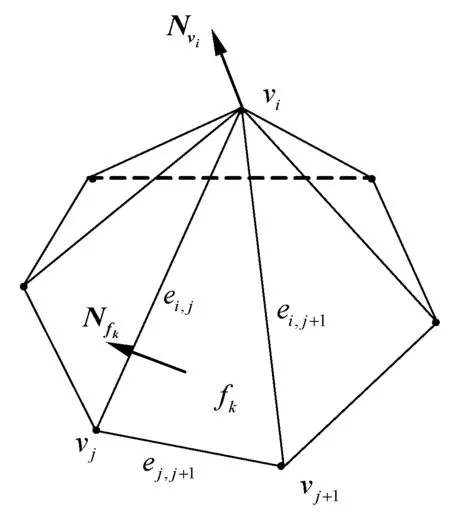
图1 法矢估计模型

然而，网格顶点法矢不仅受到相邻三角形大小的影响，还受到三角形的形状以及相邻三角形分布密度的影响。而Taubin曲率估计算法中，使用面积加权法对网格顶点法矢的计算只考虑了顶点相邻三角形的大小，忽略了三角形形状和密度的影响。目前有很多学者都提出改进的方法，如神会存等[10]在权值中加入三角面片顶点处内角。本文在Taubin的基础上提出一种新的加权方法，其表达式为：

(2)

其中，Lk为三角形周长，dj,j+1为顶点相邻三角形与顶点相对的边长，dk为三角形质心到顶点的距离。

|fk|/Lk不仅将三角形面积考虑在内，还将三角形分布密度作为影响因素包含在内，在顶点一侧区域面积一定的情况下，三角形密度越大，单个三角形面积越小，其对应的三角形周长反而相对增大，|fk|/Lk变小，这样就减小了紧密一侧三角形对顶点法矢的影响；对于狭长三角形，dj,j+1比较小，而dk比较大，这样dj,j+1/dk就会很小，从而降低了狭长三角形对法矢的影响。图2是权值改变前后，对某一网格模型局部的法矢计算结果对比，可以看出权值改变后法矢方向明显垂直于网格表面。

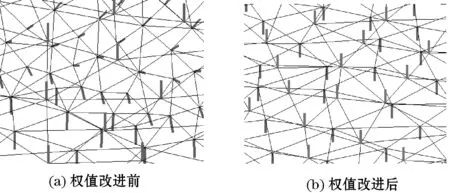
图2 权值改进前后结果对比

1.2 Householder矩阵及Givens变换

Householder矩阵的构造直接影响顶点主方向的计算。Taubin曲率算法一个关键步骤是将构造矩阵转化为对角阵，先后经过Householder变换和Givens变换，在Householder矩阵构造时，Taubin选取的Wvi阵构造方法，使得Qvi的第一列向量与顶点法矢Nvi成一个小的夹角，从而导致主方向所在平面也发生了旋转。此时的Qvi无法满足式(3)，即无法使式(4)右边矩阵的首行首列为0，降低了主方向的计算精度。

(3)

(4)

为了提高计算精度，本文利用了Nvi是构造矩阵Mvi的特征向量和其对应的特征值为0，并依据Householder矩阵的性质，采用一种新的Wvi构造方法，如下：

(5)

(6)

这样就保证了Qvi的第一列向量与顶点法矢Nvi相等向量，满足式(3)，完成对角化第一步得到式(4)。

图3为Householder矩阵改进前后对螺旋扫描体网格某型的同一局部的主方向计算结果对比。由图可以看出Householder矩阵改进后，在螺旋扫描体上两个主方向相互垂直，分别位于两个相切方向上，较符合理论实际情况，使该曲率估计精度得到了提高。

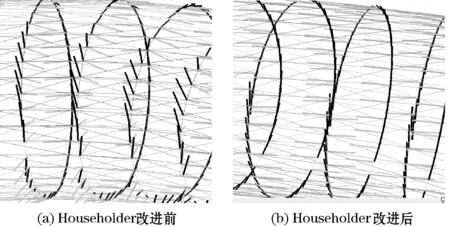
图3 Householder改进前后结果对比

在曲率估计算法中，主方向与Householder变换后的方向成一个夹角θ，需要经过Givens变换求出θ，进而获得主方向。则Givens变换为：

(7)

其中主对角线的值为：

(8)

(9)

由Givens变换副对角线值为零可以得到cosθ和sinθ值，可以获得主方向：

(10)

同样可以获得主曲率：

(11)

高斯曲率和平均曲率为：

(12)

2 特征线提取算法

本文算法利用网格模型中的三角形边分两次间接地对特征点进行提取，然后再根据提取方法的不同分类，将这些特征点分组提取为特征线，由STL文件到提取特征线过程如图4所示。

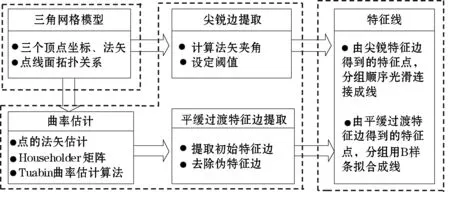
图4 提取算法流程图

主要分为三个模块：1) 三角网格模型拓扑关系重建，主要利用已有的数据结构[11-12]进行点线面关系重构；2) 特征点提取，分两次对尖锐边与平滑过渡边进行提取，通过法矢夹角运算与曲率计算识别特征边，进一步获得特征点；3) 点拟合成线，由两次得到的特征点按提取方法不同分类，各类特征点分组拟合成线。

2.1 特征边初次提取

在采样获取的三维网格模型中，只要几何特征还存在于模型中，就会留下痕迹，即凹凸边线。网格模型虽然弱化了一些特征，但对尖锐凹凸线还是会保留的，并且其三角形的边与特征线方向基本上保持一致。

在三角网格模型中，尖锐边相邻的两个三角面片夹角比较小，随着尖锐特征减缓，其夹角也逐渐增大；当夹角小于预设定的阈值时，则将该边标识为特征边，反之则不作标识，一般阈值设置为120。两个三角面片的夹角与其法矢夹角成互补关系，所以可以用法矢夹角大小来识别特征边；此时的阈值也与三角面片的阈值成互补关系，即法矢夹角大于此时的阈值(60)时识别为特征边，夹角越大，则边越尖锐，这样可以方便地提取网格模型中的尖锐边。

该方法计算简单，运行速度快，减少了耗费时间的曲率计算，对一些简单零件模型可以直接满足要求。但对于零件中的平缓过渡的特征边无法处理，还需要采用曲率与凹凸性关系的方法来识别三角面片之间的平滑过渡特征线。

2.2 二次提取特征边

平缓过渡特征边通常连接两个没有明显分界的曲面，该类特征边特征不明显，提取比较困难。文献[7,13]利用曲率判断该边上的点是否为极值点的方法来处理这种特征边，这种方法计算量大，处理时间长。本文利用平均曲率与凹凸性的关系来处理这种特征边，避免了对极值的判断，降低了计算量。

Besl等[14]根据高斯曲率与平均曲率的正负将点的局部曲面分为了9类，任意复杂曲面都可以由这些曲面组合而成，而平缓过渡特征边通常就是这些曲面的分界边，表1仅给出了平均曲率与曲面凹凸性的关系。

表1 平均曲率与曲面凹凸性关系

如图5所示，两个相邻三角形存在一个公共边ei,j，其两个端点分别为vi和vj，vi+1和vj+1称为该边相对的两个顶点。由表1可知，判断ei,j是否为特征边只需要比较该边相对的两顶点vi+1和vj+1的平均曲率与0的大小。本文采用区间(-0.01, 0.01)代替0值，这样能够形成三个区间，若两点的平均曲率值分别属于两个不同的区间，则将该边进行标识。

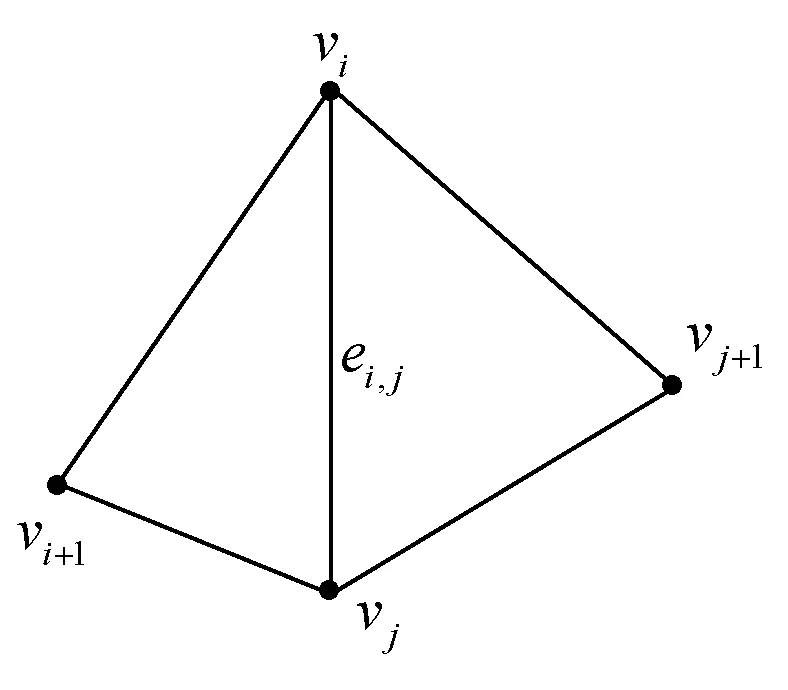
图5 边与相对点模型

尖锐边上的顶点，即初次提取的特征边上的顶点，这些顶点的曲率都是由差别很大曲面甚至尖锐边上的顶点估计出来的，可能会导致了这些点的曲率估计误差较大。若vi+1和vj+1取到这些点，可能会对边的判断产生较大的误差，本文如果采用出现这种情况，则直接放弃对该边的标记。

经过上述过程，一些因为网格化而形成的凸凹特征边也会被提取出来，里面存在一些伪特征边，需要将其分离出来以得到真正的特征边，因此除去伪特征边是必不可少的一步。通常判断一个点是否为特征点, 就是判断该点的曲率在主方向上是否为极值点[13]。本文基于这种思想定义了边的主方向，并利用边的主方向与边的夹角关系来除去伪特征边。

边的主方向：在网格模型中，边是由两个顶点连接而成，用这两个顶点主方向的矢量和作为该边的主方向，如下式：

PD=PD1+PD2

(13)

其中PD为边的主方向，PD1和PD2为边两个端点的主方向，矢量和示意如图6所示，这样定义边的主方向既减小了以单个顶点作为边的主方向所引起的误差又可以将边的变化趋势合理反应出来。

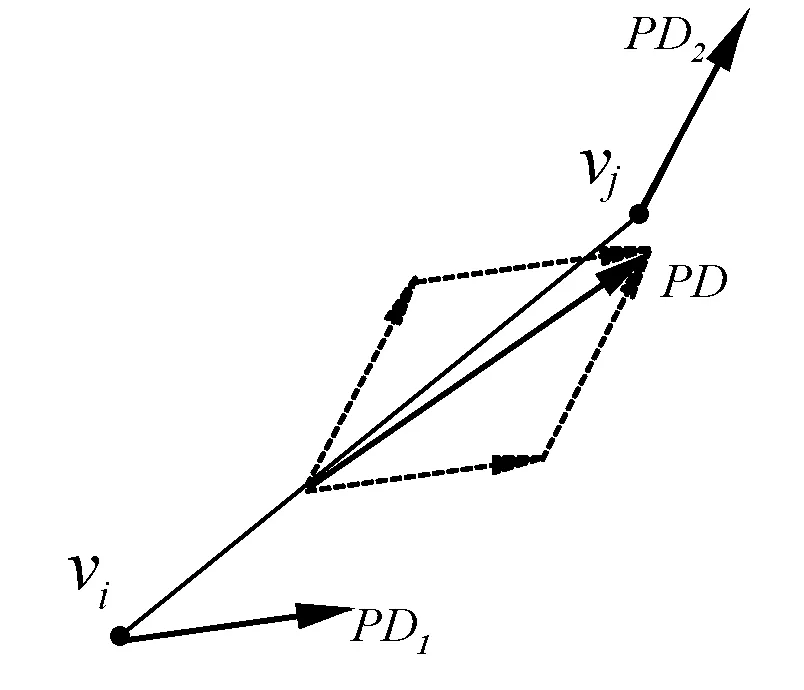
图6 边主方向计算示意图

当边的方向与边的主方向中的其中一个一致时，就将该边标识为特征边。在三角网格模型中，边与边主方向不可能完全一致，会成一个夹角关系,因此，本文设置了一个区间(0, 30)，当夹角在这个区间范围内时，就判定该边为特征边，否则就去除该边。

2.3 获取特征线

以上得到的特征边都是由三角形边组成的，这些边的顶点通过去除冗余点后就组成了特征点集合。文献[7]将这些特征点排序后分组拟合成B样条，由于B样条拟合会消除尖角处特征，那么两条特征线的夹角处特征就有可能被消除，如图7所示。

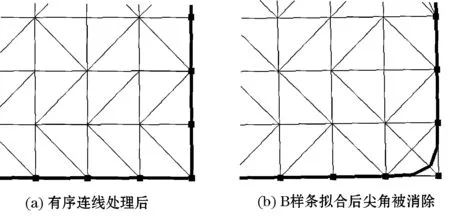
图7 尖角特征被消除

本文根据两次提取方法不同将特征点分成两类，一类是由尖锐边得到特征点，另一类是由平缓过渡边得到的特征点。对第一类特征点做分组有序连接线处理；另一类采用了刘胜兰等[7]的方法分组拟合成B样条曲线。

2.4 算法实现描述

本文整体提取算法步骤如下：

输入： STL文件格式数据。

输出： 三角网格模型特征线。

Step1 读入STL文件格式数据，并建立点、边、面之间的拓扑关系，分别储存于点表、边表和面表中。

Step2 提取尖锐特征边。边e两邻面法向量n1和n2，夹角φ= ，阈值θ，若φ>θ，标识该边为特征边，存在边数组EArray1中。

Step3 提取平缓过渡特征边。

Step3.1 利用改进后的Taubin曲率估算法估算顶点曲率。

Step3.2 根据平均曲率与凹凸性的关系，并以尖锐特征边顶点作为限制条件提取初始特征边。

Step3.3 去除伪特征边，并将特征边保存在边数组EArray2中。

Step4 将EArray1和EArray2中边的顶点分别保存在特征点数组Array1和Array2中，并分类分组处理拟合成线。

在Step2中的尖锐边不包括边界边，边界边可由一条边的相邻三角形个数进行判断[15]，这里不再赘述。

3 实 例

为了验证本算法的有效性，本文算法通过Visual C++ 2008和OpenGL开发平台编程实现，实验环境是Windows XP操作系统，主频2.6 GHz，内存为2.0 GB，为了更能说明本文算法提取结果的有效性，采用的文献[7]的算法进行对比分析。

表2给出两种模型基本信息和文献[7]算法与本文算法分别耗用的时间。图8、图9分别给出了利用文献[7]算法和本文算法对表1中的齿轮模型与大象模型分别提取特征线后的结果对比图。

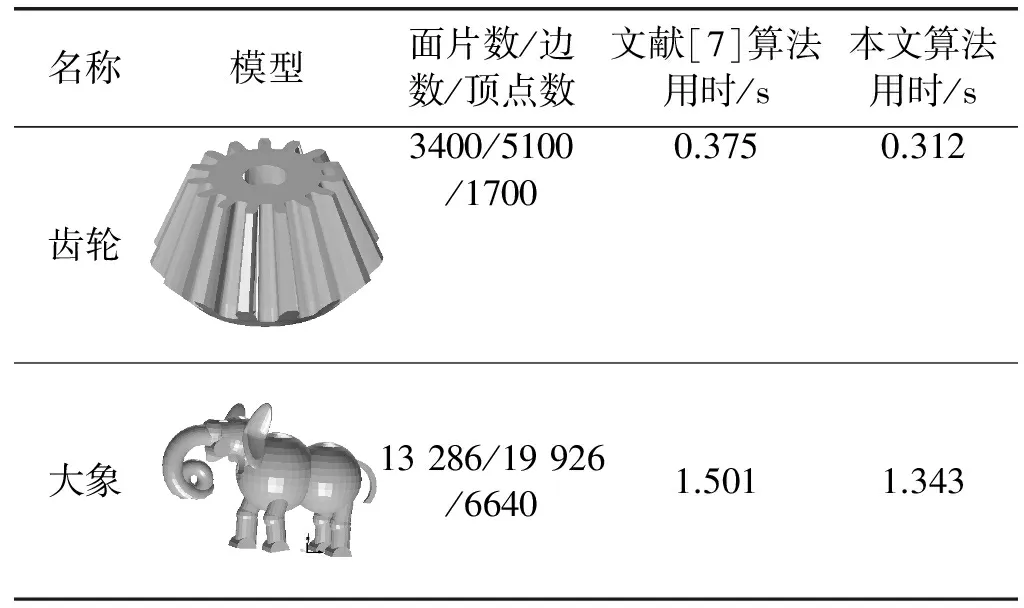
表2 模型特征线提取算法时间耗费

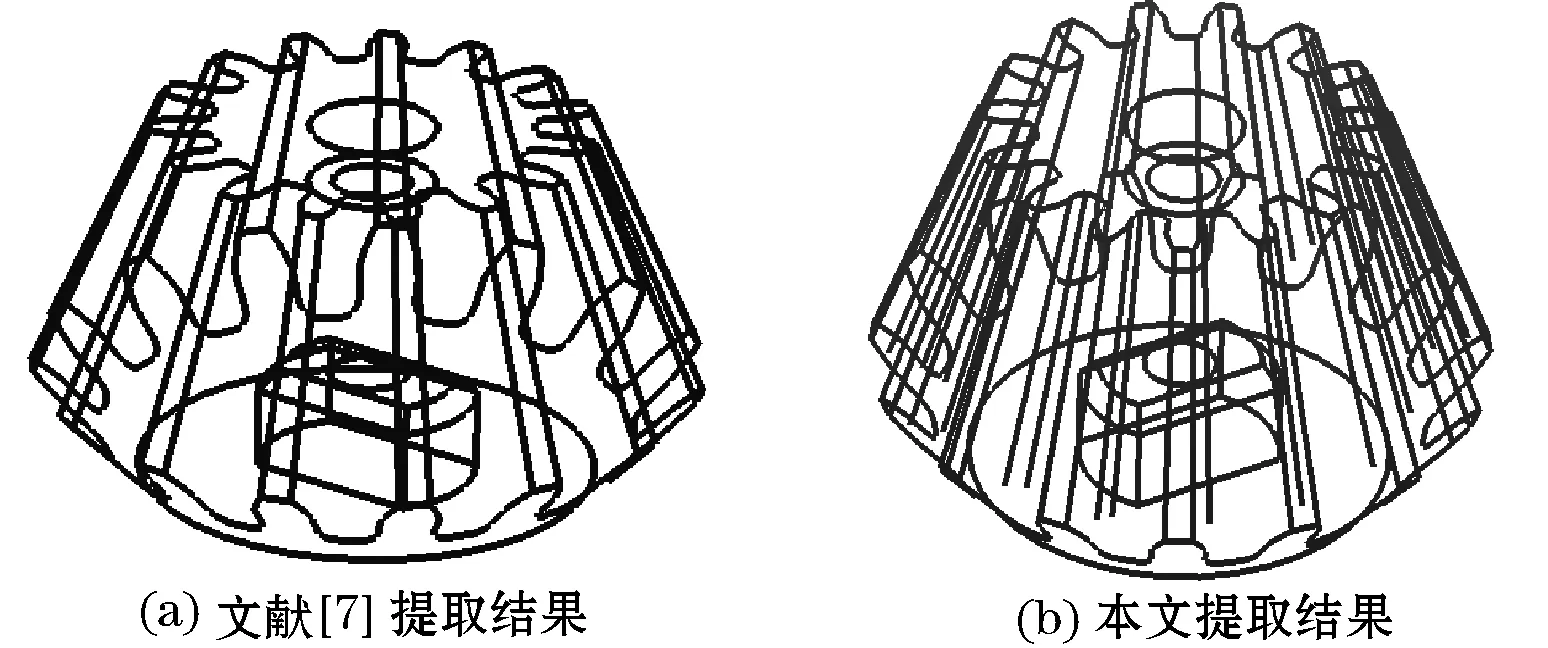
图8 齿轮模型两种算法对比图

图9 大象模型两种算法对比图

经过对两种算法的对比分析，本文算法与文献[7]算法识别的模型轮廓基本一致，有力地说明了本文算法的有效性。此外本文算法还可以有效地识别一些不易被识别出的平滑过渡线，如齿轮齿根处的过渡线，大象鼻子处的轮廓线；在光顺性方面，本文算法识别效果也比较突出，整体光顺性比文献[7]的有所提高。

在整个计算过程中，两种算法都进行了曲率估计，文献[7]运用曲面拟合，计算量大，本文使用离散估计，大大地减少了计算量。此外，相对于文献[7]中的算法，本文并没有直接对特征点进行判断，而是通过特征边间接地得到特征点，在此方面也减少了计算量，提高了算法效率。

4 结 语

本文对Taubin曲率算法做出了一些改进，并在此基础上提出了一种新的特征线提取算法。该算法充分利用了三角形法矢以及平均曲率与凹凸性的关系，分两次提取特征点，最后对特征点进行拟合成线处理。实验表明，该算法对网格模型特征线提取效果较好，尤其是对机械零件的特征线提取，直接跳过了对顶点的判断，减少了计算量。但是对含有大量噪声的模型或自然网格模型等网格模型提取结果连续性较差，有待进一步提高，下一步重点对此进行研究。

[1] Razdan A, Bae M. A hybrid approach to feature segmentation of triangle meshes[J]. Computer-Aided Design, 2003, 35(9):783-789.

[2] Wang J, Yu Z. Surface feature based mesh segmentation[J]. Computers & Graphics, 2011, 35(3):661-667.

[3] 韩丽, 高小山, 楚秉智. 离散曲率约束的三角网格模型拓扑分割算法[J]. 计算机辅助设计与图形学学报, 2009, 21(6):831-835.

[4]KimHS,ChoiHK,LeeKH.Featuredetectionoftriangularmeshesbasedontensorvotingtheory[J].Computer-AidedDesign, 2009, 41(1):47-58.

[5] 张慧娟, 耿博, 汪国平. 采用张量投票理论的三角网格特征边提取算法[J]. 计算机辅助设计与图形学学报, 2011, 23(1):62-70.

[6]MilroyMJ,BradleyC,VickersGW.Segmentationofawrap-aroundmodelusinganactivecontour[J].Computer-AidedDesign, 1997, 29(4):299-320.

[7] 刘胜兰, 周儒荣, 张丽艳. 三角网格模型的特征线提取[J]. 计算机辅助设计与图形学学报, 2003, 15(4):444-448,453.

[8]RazdanA,BaeM.CurvatureestimationschemefortrianglemeshesusingbiquadraticBézierpatches[J].Computer-AidedDesign，2005, 37(14):1481-1491.

[9]TaubinG.Estimatingthetensorofcurvatureofasurfacefromapolyhedralapproximation[C]//Proceedingsofthe5thInternationalConferenceonComputerVision, 1995:902-907.

[10] 神会存, 李建华, 周来水. 三角网格模型顶点法矢与离散曲率计算[J]. 计算机工程与应用, 2005(26):12-15.

[11]SiegerD,BotschM.Design,implementation,andevaluationofthesurfacemeshdatastructure[C]//Proceedingsofthe20thInternationalMeshingRoundtable.Heidelberg:Springer, 2011:533-550.

[12]GurungT,LuffelM,LindstromP,etal.Zipper:Acompactconnectivitydatastructurefortrianglemeshes[J].Computer-AidedDesign, 2013, 45(2): 262-269.

[13]YangM,LeeE.Segmentationofmeasuredpointdatausingaparametricquadricsurfaceapproximation[J].Computer-AidedDesign, 1999, 31(7):449-457.

[14]BeslPJ,JainRC.Segmentationthroughvariable-ordersurfacefitting[J].IEEETransactionsonPatternAnalysisandMachineIntelligence, 1988, 10(2):167-192.

[15]JunY.Apiecewiseholefillingalgorithminreverseengineering[J].Computer-AidedDesign, 2005, 37(2):263-270.

A FEATURE LINE EXTRACTION METHOD COMBINING MEANCURVATURE WITH MESH EDGES

Wang Qinrui Zhang Yingzhong Luo Xiaofang

(SchoolofMechanicalEngineering,DalianUniversityofTechnology,Dalian116024,Liaoning,China)

With the development of digital geometry technology, a large number of complex shapes are represented by the mesh model. It is the basic work for follow-up geometry and feature recognition to identify and extract feature lines. Thus, a feature line extraction method combining mean curvature with mesh edges is presented. Firstly, the angle between the normal of adjacent triangles is used for the initial extraction of sharp edges. Then the feature edges are extracted according to the relationships between concave-convex properties and mean curvature of the surface. Finally the vertices of the extracted feature edges are classified and linked into feature lines. The case study verifies that the proposed algorithm can extract sharp edges and transition feature edges efficiently and effectively.

Feature line extraction Triangular mesh model Curvature estimation Reverse engineering

2015-11-11。国家自然科学基金项目(51375069)。王钦瑞，硕士生，主研领域：数字网格分割及特征重构。张应中，副教授。罗晓芳，副教授。

TP391.41

A

10.3969/j.issn.1000-386x.2017.01.043