帯边际风险控制的投资组合问题的半定规划松弛
丁晓东,肖琳灿,罗和治
(1.浙江工业大学 理学院,浙江 杭州 310023;2. 浙江工业大学 经贸管理学院,浙江 杭州 310023)
帯边际风险控制的投资组合问题的半定规划松弛
丁晓东1,肖琳灿1,罗和治2
(1.浙江工业大学 理学院,浙江 杭州 310023;2. 浙江工业大学 经贸管理学院,浙江 杭州 310023)
边际风险衡量单个资产对投资组合总体风险的贡献,是投资组合和风险管理中的一个重要准则.考虑均值方差框架下带有边际风险控制的投资组合选择问题,其优化模型是一个非凸二次约束二次规划问题.通过探索模型的结构特点并结合提升方法和割不等式技术,给出了带有边际风险控制的均值方差投资组合选择模型的一个紧的半定规划松弛,分析了它与原问题的最优解和最优值之间的关系以及它与文献中的凸二次规划松弛所提供下界的比较关系.初步数值结果表明基于半定规划松弛的分支定界算法能有效地找到原问题的全局解.
投资组合;边际风险;半定规划松弛;分支定界
投资组合理论主要研究如何在收益不确定的情况下进行资产有效配置以最大化预期收益同时最小化风险.MARKOWITZ[1]在1952年采用均值和方差度量投资组合的预期收益和风险,提出了均值方差投资组合优化模型,奠定了现代投资组合理论的基础.LI等[2-3]分别将均值方差模型推广到多阶段投资组合和带有破产风险控制的动态投资组合问题.PARDALOS等[3]综述了投资组合选择的优化模型.自均值方差模型提出后,基于不同视角的新的风险度量方法和投资组合模型被相继提出.KNONO等[5]采用均值绝对偏差度量风险,建立均值绝对偏差投资组合模型,该模型可转化为线性规划来求解.YOUNG[6]采用投资组合可能出现的最坏收益作为风险度量,基于历史数据给出了极大极小投资组合模型,并通过引入变量替换方法将该模型转化为线性规划来求解.PHILIPPE等[7]利用风险值(Value-at-risk, VaR)来衡量一定置信度下投资组合所面临的最大损失.ALEXANDER[8]证明了在各资产的收益服从正态分布的假设下,带有VaR约束的投资组合模型可转化为等价的二阶锥规划问题.值得指出,这些风险度量方法仅考虑投资组合的总体风险,而忽略了单个资产对投资组合总体风险的贡献.边际风险来衡量单个资产对投资组合的总体风险的贡献,单个资产的边际风险定义为整个投资组合的风险与不包含该资产的投资组合的风险之差;GRINOLD等[9]将单个资产的边际风险定义为投资组合的收益标准差关于该资产持有量的偏导数.但遗憾的是,这些定义都有一个共同缺点:所有资产的边际风险之和不等于投资组合的总体风险.为克服这个缺点,ZHU等[10]通过分解资产收益的协方差矩阵提出了一个新的边际风险定义,建立了带有边际风险控制约束的均值方差投资组合选择模型,但该模型是一个带非凸二次约束的二次规划(QCQP)问题,求它的全局解是NP-难的;并给出了该模型的一个凸二次规划松弛和基于该松弛的分支定界全局算法.
寻找非凸QCQP问题全局解的常用方法是基于线性规划与二次凸松弛的分枝-定界方法,而分枝-定界方法的关键问题是如何有效地计算紧的下界.我们知道,半定规划(简记SDP)松弛对非凸QCQP问题可以提供更紧的下界.ZHENG等[11-12]研究了非凸QCQP的基于D.C.分解、矩阵锥分解和多胞形逼近等技术的SDP松弛方法;蔡伟荣等[13]利用矩阵分解方法研究了0-1二次规划的SDP松弛.为此,我们针对模型的结构特点并结合提升方法和割不等式技术,给出了带有边际风险约束的均值方差投资组合模型的一个紧的SDP松弛,讨论了它与原问题的最优解和最优值之间的性质以及它与文献[10]中的凸二次规划松弛所提供下界的比较关系.初步数值结果表明:基于SDP松弛的分支定界算法能在较短时间内求得模型的全局解,比文献[10]中全局算法的求解效率更高.
1 带边际风险控制的投资组合模型
描述文献[10]所提出的带有边际风险约束的均值方差投资组合选择模型.假设市场上有n个风险资产,r=(r1,r2,…,rn)T表示资产收益随机向量,其中ri表示第i个资产的收益随机变量.给定投资组合x=(x1,x2,…,xn)T,则投资组合x的收益随机变量可表为p(x)=rTx,其预期收益和方差可分别表为
μ(x)=E(rTx)=μTx
σ(x)=E(rTx-μ(x))2=xTQx
其中:μ∈Rn和Q=(σij)n×n∈Rn×n分别为资产收益r的均值向量和协方差矩阵.以预期收益μ(x)和方差σ(x)为双目标的均值方差投资组合模型可表为
(PMV) minτxTQx-μTxs.t.x∈D={x∈Rn:eTx=1,l≤x≤u}其中:e=(1,1,…,1)T,τ∈(0,∞)分别为风险厌恶参数,l,u∈Rn.然而,均值方差投资组合模型的弊端是未考虑单个资产对投资组合总体风险的贡献.为此,文献[10]给出了如下的边际风险的定义.
定义1 投资组合x=(x1,x2,…,xn)T的第k个资产的边际风险记为

(1)
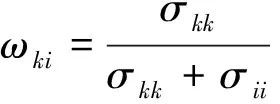

(PMR) minf(x)=τxTQx-μTxs.t.xTQkx≤ρkk=1,2,…,mx∈D
其中ρk(k=1,2,…,m,m≤n)为给定的第k个资产的边际风险容忍参数.需要指出的是,由于Qk为不定矩阵,问题(PMR)是一个非凸二次约束二次规划问题,求它的全局最优解是NP-难的.
引入如下记号:记v(·)为优化问题(·)的最优值,记Sn为n×n对称矩阵的集合.设A,B∈Sn,AB表示A-B是为半正定矩阵,Sn中的内积定义为A·B=Tr(AB).
2 半定规划松弛
给出模型(PMR)的一个SDP松弛及其性质,并讨论它与文献中已有的凸二次规划松弛的比较关系.根据Qi的定义可知:Qi为秩2矩阵,用特征值分解方法将其分解为
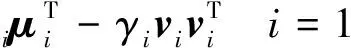
(2)
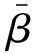

i=1,2,…,m
(3)
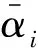

i=1,2,…,m
注意到当eTx=1时E·xxT=(eTx)2=1,其中E=eeT.另外,注意到xTQx=Q·xxT且xTQix=Qi·xxT.于是,令X=xxT并将其松弛为半定约束X-xxT0,我们可以得到问题(PMR)的一个SDP松弛为
(SDPMR) minτQ·X-μTxs.t.eTx=1,E·X=1Qi·X≤ρii=1,2,…,m

X-xxT0,l≤x≤u
首先,讨论问题(PMR)与其松弛(SDPMR)的最优解和最优值之间的关系.

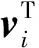


(4)
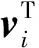

(5)

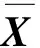
(6)
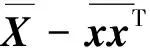

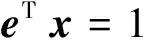


其次,我们讨论SDP松弛与文献[10]中所提出的凸二次规划松弛的比较关系.文献[10]先利用式(2)将问题(PMR)中的边际风险约束xTQix≤ρi,i=1,2,…,m改写为

i=1,2,…,m
(7)
(QPMR) minτxTQx-μTxs.t.eTx=1,l≤x≤u

i=1,2,…,m
我们有
定理3v(SDPMR)≥v(QPMR)

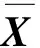


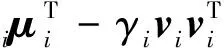


i=1,2,…,m

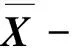
定理3证明了问题(SDPMR)比(QPMR)提供更紧的下界.注意到从下节的数值结果看到,对所有数值例子不等式v(SDPMR) 首先,给出模型(SDPMR)和(QPMR)对问题(PMR)提供下界的比较数值结果.数值测试在Matlab R2013b上实现,在PC机(3.33 GHz,8 GB,RAM)上运行,并用CVX 1.2中的SDPT3求解器来求解计算下界的SDP模型,用CPLEX 12.6中的QP求解器来求解计算下界的QP模型. 测试问题由文献[11]给出的随机方法生成.令ri=αi+βirM+δi,i=1,2,…,n,其中:ri为第i个资产的收益;rM市场指数的收益;δi为第i个资产收益的残差.从而可得到μi=αiβiE(rM),σii=Var(rM)+Var(δi),且σij=βiβjVar(rM),其中:参数αi=0.000 001×ra,rd为用正态随机分布生成的,i=1,2,…,m;βi为在[0.6,1.2]上用均匀分布随机生成的,i=1,2,…,m;E(rM)=0.02,Var(rM)=0.003,且Var(δi)是在[0,0.002]上用均匀分布随机生成的,i=1,2,…,m.再令l=(0,0,…,0)T,u=(1,1,…,1)T,τ=1.为了衡量下界的紧性,定义下界的改进率为 表1给出了对(PMR)的具有相同规模的10个测试问题的下界的平均改进率.从表1可看到:在所有的测试问题中,下界v(SDP}MR)比v(QPMR)更紧,且当ρi=0.003/n时测试问题的平均改进率提高更大. 表1 对问题(PMR)下界的平均改进率 Table 1 The average improvement ratio of lower bound for (PMR) nmR/%Pi=0.01/nPi=0.003/n10102.839.4720203.7013.8630304.8716.6040405.3517.9550505.3117.6660605.0918.2370704.9818.8280804.7918.6190904.7918.521001004.4618.38 其次,给出求问题(PMR)全局解的基于SDP和二次凸松弛的分支定界算法的比较数值结果. 记“BB-QP”为文献[11]中所提出的基于二次凸松弛(QPMR)的分支定界算法,而“BB-SDP”为下界由SDP松弛(SDPMR)得到的分支定界算法.表2给出了BB-SDP和BB-QP算法对5个测试问题的平均数值结果,其中“fval”,“iter”,“cpu”分别为算法对5个测试问题得到的平均最优值、平均迭代次数和平均CPU时间(单位:s).从表2可见:BB-SDP算法能有效地找到所有测试问题的全局解,而且比BB-QP算法所需时间更短. 表2 BB-SDP和BB-QP对5个测试问题的平均数值结果 Table 2 The average numerical results of BB-SDP and BB-QP for five test problems nmBB⁃QPfvalitercpuBB⁃SDPfvalitercpu105-0.017850.43.0-0.01781.00.41010-0.0182144.47.4-0.01821.00.1205-0.018726.41.5-0.01871.00.12010-0.0191131.87.7-0.01911.00.23010-0.018949.63.2-0.01891.00.23020-0.0186376.826.8-0.01851.00.34010-0.0189103.47.2-0.01891.00.34020-0.0187349.227.2-0.01871.00.45010-0.0190129.410.9-0.01901.00.45020-0.0191149.612.4-0.01911.00.66010-0.019173.26.8-0.01911.00.66020-0.0190273.627.9-0.01901.00.87010-0.019282.08.3-0.01911.00.77020-0.0191226.025.4-0.01911.01.18010-0.019430.03.6-0.01931.00.98020-0.019356.86.1-0.01931.01.29010-0.019225.23.3-0.01921.01.19020-0.0194209.228.9-0.01921.01.810010-0.019425.43.2-0.01941.01.410020-0.0193171.623.2-0.01931.02.210050-0.01921050.0224.4-0.01921.07.0 考虑了带有边际风险控制约束的投资组合选择问题,其优化模型是一个非凸二次约束二次规划问题,但求它的全局解一般而言是非常困难的.利用非凸约束的特殊结构并结合提升法和添加割不等式技术,给出了该模型的一个更紧的SDP松弛及其最优解的性质,证明了它比文献[10]中的二次凸松弛更紧.初步数值结果表明:基于SDP松弛的分支定界算法能在较短时间内求得由随机产生的测试问题的全局解,比文献[10]中的全局算法更有效. [1] MARKOWITZ H M. Portfolio selection[J]. Journal of finance,1952,7:77-91. [2] LI D, NG W L. Optimal dynamic portfolio selection: multi-period mean-variance formulation[J]. Mathematical finance,2000,10:387-406. [3] ZHU S S, LI D, WANG S Y. Risk control over bankruptcy in dynamic portfolio selection: a generalized mean-variance formulation[J]. IEEE transactions on automatic control,2004,49:447-457. [4] PARDALOS P, SANDTSAR M, ZOPOUNIDIS C. On the use of optimization models for portfolio selection: a review and some computational results[J]. Computational economics,1997,7:227-244. [5] KONNO H, YAMAZAKI H. Mean-absolute deviation portfolio optimization model and its applications to Tokyo stock market[J]. Management science,1991,37:519-531. [6] YOUNG M R. A minimax portfolio rule with linear programming solution[J]. Management science,1998,44:673-683. [7] PHILIPPE J. Value at risk: the new benchmark for controlling market risk[M]. Chicago:Irwin Professional Publishing,1996. [8] ALEXANDER G J, BAPTISTA A M. A comparison of VaR and CVaR constraints on portfolio selection with the mean-variance model[J]. Management science,2004,50(9):1261-1273. [9] GRINOLD R C, KAHN R N. Active portfolio management: a quantitative approach for producing superior returns and controlling risk[M]. New York: McGraw-Hill,1999. [10] ZHU S S, LI D, SUN X L. Portfolio selection with marginal risk control[J]. The journal of computational finance,2010,14(1):3-28. [11] ZHENG X J, SUN X L, LI D. Convex relaxations for nonconvex quadratically constrained quadratic programming: matrix cone decomposition and polyhedral approximation[J]. Mathematical programming,2011,129(2):301-329. [12] ZHENG X J, SUN X L, LI D. Nonconvex quadratically constrained quadratic programming: best D.C. decompositions and their SDP representations[J]. Journal of global optimization,2011,50(4):695-712. [13] 蔡伟荣,柳叶,罗和治.基于矩阵分解的0-1二次规划的SDP松弛[J].浙江工业大学学报,2015,43(5):582-586. Semidefinite programming relaxation for portfolio selection with marginal risk control DING Xiaodong1, XIAO Lincan1, LUO Hezhi2 (1.College of Science, Zhejiang University of Technology, Hangzhou 310023, China;2.College of Economics and Management, Zhejiang University of Technology, Hangzhou 310023, China) Marginal risk that is used to measure the contribution of an individual assets to the overall risk of the portfolio, is an important criterion in portfolio selection and risk management. In this paper, we consider the portfolio selection problem with marginal risk control in the mean-variance framework. In this problem, the optimization model is a quadratic programming problem with nonconvex quadratic constraints. By exploiting the structural characteristics of the model and combining the lifting method with secant inequality techniques, we present a tight semidefinite programming (SDP) relaxation for this problem. We discuss the relationships between optimal solutions and optimal values of the original problem and its SDP relaxation, and compare the lower bounds provided by the SDP relaxation and quadratic convex relaxation in the literature. Preliminary numerical results show that the branch-and-bound algorithm based on the SDP relaxation can find the global optimal solution of the original problem effectively. portfolio selection; marginal risk; semidefinite programming relaxation; branch-and-bound (责任编辑:刘 岩) 2016-04-12 国家自然科学基金资助项目(11371324);浙江省自然科学基金资助项目(LY17A010023) 丁晓东(1983—),男,河南郑州人,讲师,博士,研究方向为最优化理论、算法与应用,E-mail: dxdopt@zjut.edu.cn. O221.2 A 1006-4303(2017)01-0064-053 数值结果


4 结 论

