基于可变形部件模型的粒子滤波快速行人检测与跟踪
王传旭 郝艳婷
(青岛科技大学信息科学技术学院 山东 青岛 266061)
基于可变形部件模型的粒子滤波快速行人检测与跟踪
王传旭 郝艳婷
(青岛科技大学信息科学技术学院 山东 青岛 266061)
针对视频中的行人检测和跟踪问题,提出一种基于可变形部件模型的快速行人检测、改进粒子滤波的行人跟踪算法。在行人检测阶段,为了改善非刚体行人的检测精度,采用了混合多尺度可变形部件模型;同时为了加速行人底层特征的计算,采用了基于预测算法的快速特征金字塔计算行人特征,代替传统的计算图像特征金字塔的每一个尺度特征。在行人跟踪阶段,采用时变的状态空间模型和基于颜色梯度直方图的观测模型对检测到的行人进行跟踪。实验证明,改进的行人检测算法可以在性能损失忽略不计的条件下,大大提高检测速度,并且相对于传统的行人跟踪,改进的粒子滤波算法对行人这一非刚性目标能实现较好的跟踪。
行人检测 行人跟踪 可变形部件模型 快速特征金字塔 粒子滤波
0 引 言
近年来,基于视频的行人检测和跟踪受到了国内外研究学者的广泛关注。虽然现在已经有了丰硕的研究成果,但是还存在很多难点,如:行人自身的非刚性和运动的随机性[1-3],观测模型鲁棒性,多人跟踪的复杂性和行人跟踪系统实时性的问题[13]等,导致视频行人跟踪成为一个相当复杂的问题。针对这些难点,本文主要做了如下改进。
在行人检测阶段,采用Felzenszwalb等人提出的混合多尺度可变形部件模型[1],在PascalVOC数据集上训练得到混合人体模型。比较传统的行人检测,该模型大大提高了非刚性行人的检测精度。除此之外,采用基于预测算法的快速特征金字塔计算行人特征[1],代替传统的计算每一个尺度的特征[8],比较传统方法与快速计算方法的运算量,结果表明快速特征金字塔计算方法具有明显的优势。
检测到待跟踪行人后,采用基于粒子滤波的原理[5]对行人进行跟踪。由于传统粒子滤波的状态空间模型是时不变的,难以适应非匀速运动的行人目标,因此跟踪效果不佳。对此,跟踪阶段采用非匀速的状态空间模型代替传统的匀速运动模型,使其随着行人目标运动速度变化的情况不断调整,以适应在不同时间段内的运动状况,从而使该模型对行人目标运动情况的描述更为准确;同时,行人跟踪的观测模型采用颜色梯度方向直方图,这种观测模型不仅包含行人的颜色信息,还包含行人的纹理信息,使两帧之间的行人匹配更精确。
1 快速行人检测
1.1 混合多尺度可变形部件模型
相对于传统的行人检测器,可变形部件模型可适应行人目标的很多外表变化,如行人较多且间距较近、不同姿势变化、观察视角变化等,因此,在复杂场景下可以得到更高的检测精度。为了提高检测模型的鲁棒性,本文采用混合多尺度可变形部件模型来适应变化丰富的非刚性行人检测。
图1为行人检测阶段使用的人体模型,每一行是一个DPM。DPM为星型结构,包括一个粗糙的根滤波器和一系列高分辨率的部件滤波器以及相应的可变形模型构成。

图1 含有3个组件的混合人体模型
其中,第一列为粗糙的根滤波器,第二列为高分辨率的部件滤波器,第三列为每个部件相对于根滤波器的空间位置模型。前两列的可视化滤波器表示特征在不同方向的正权重,第三列的空间位置模型的可视化图表示将部件滤波器的中心放置到相对根滤波器的不同位置时产生的变形损耗,越白则变形损耗越高,即部件滤波器偏离其理想位置越远。
该行人模型的训练环境包括:Matlab版本Matlab2012b,c++编译器VS2010,训练数据集PascalVOC(包括训练验证集VOCtrainval_06-Nov-2007和测试集VOCtest_06-Nov-2007),VOC开发包VOCdevkit_08-Jun-2007。该模型在训练之前需要在VS2010中生成learn.exe。
1.2 快速特征金字塔原理
基于混合多尺度可变形部件模型的行人检测系统采用HOG特征金字塔计算行人特征,为了提高检测速度,本文采用快速特征金字塔计算行人特征,代替DPM检测系统中计算图像特征金字塔每一个尺度的特征。具体原理描述如下:

(1)

图2 快速特征金字塔原理图
只计算每组一个尺度,为速度与精确度之间提供了一个好的权衡,而且计算量显著减少。假设,计算Ω的运算量与n×n图像像素数量呈线性关系。构造每组m个尺度的特征金字塔的运算量是:
(2)

本文的行人检测系统采用FHOG表征行人特征,近似计算特征FHOG的λΩ的估计结果如图3所示。
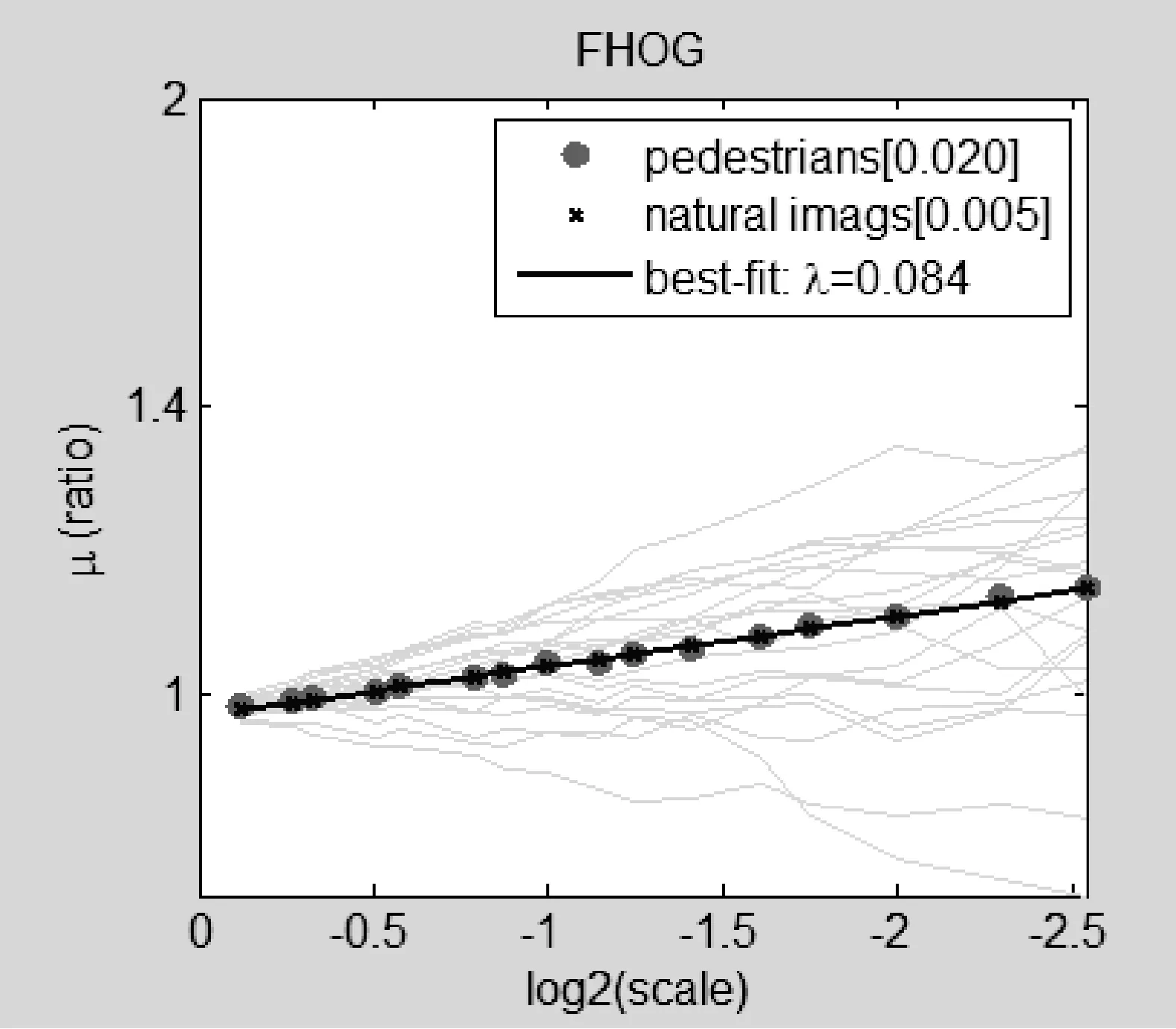
图3 FHOG特征缩放的幂次定律
图3描绘了在行人与自然图像集(选用INRIA数据集)中FHOG特征缩放的幂次定律,括号内的值为预测值和观测值的期望误差。从图中可以看出,μs与s′在对数坐标空间中呈线性关系,并且λΩ=0.084。
2 改进粒子滤波的行人跟踪
2.1 状态空间模型
传统的基于粒子滤波行人跟踪包括两个模型:状态空间模型和观测模型。其中,状态空间模型是时不变的,难以适应跟踪行人的运动变化情况。对此提出改进措施,用时变的状态空间模型代替传统的时不变模型,以适应行人在不同时间段内运动速度的变化,提高了粒子传播的有效性和指导性。具体原理介绍如下:
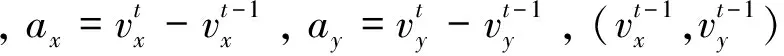
当行人运动加速度加快时,ax、ay相应增大,粒子传播范围增大,反之亦然。改进后的状态空间模型随着行人目标运动速度的变化趋势而改变,更加贴近行人的实际运动状况,从而为粒子在t+1时刻的传播提供更精确的预测。
2.2 观测模型
传统粒子滤波的观测模型采用颜色直方图对行人进行建模,由于颜色直方图没有包含行人的空间信息和纹理信息,因此无法精确地跟踪行人。对此,本文采用颜色梯度方向直方图表征行人特征,即在梯度方向上结合梯度强度和颜色值。具体原理介绍如下:
首先将快速算法检测到行人或粒子传播跟踪到的行人转换为灰度图,计算每个像素点的梯度幅值M和方向θ,然后将不同的梯度幅值划分到直方图级数中,最后结合行人的颜色信息,建立颜色梯度方向直方图:
(3)
其中,D为要划分的直方图级数,L为要划分的颜色级数,δ为Kroneckerdelta函数,C为归一化系数,C=∑(x,y)M(x,y)。
本文采用Bhattacharyya距离作为行人模型的相似度度量。Bhattacharyya系数ρ越大越相似。
ρ=ρ[H(d,l),HC(d,l)]
(4)
2.3 行人跟踪的算法框架
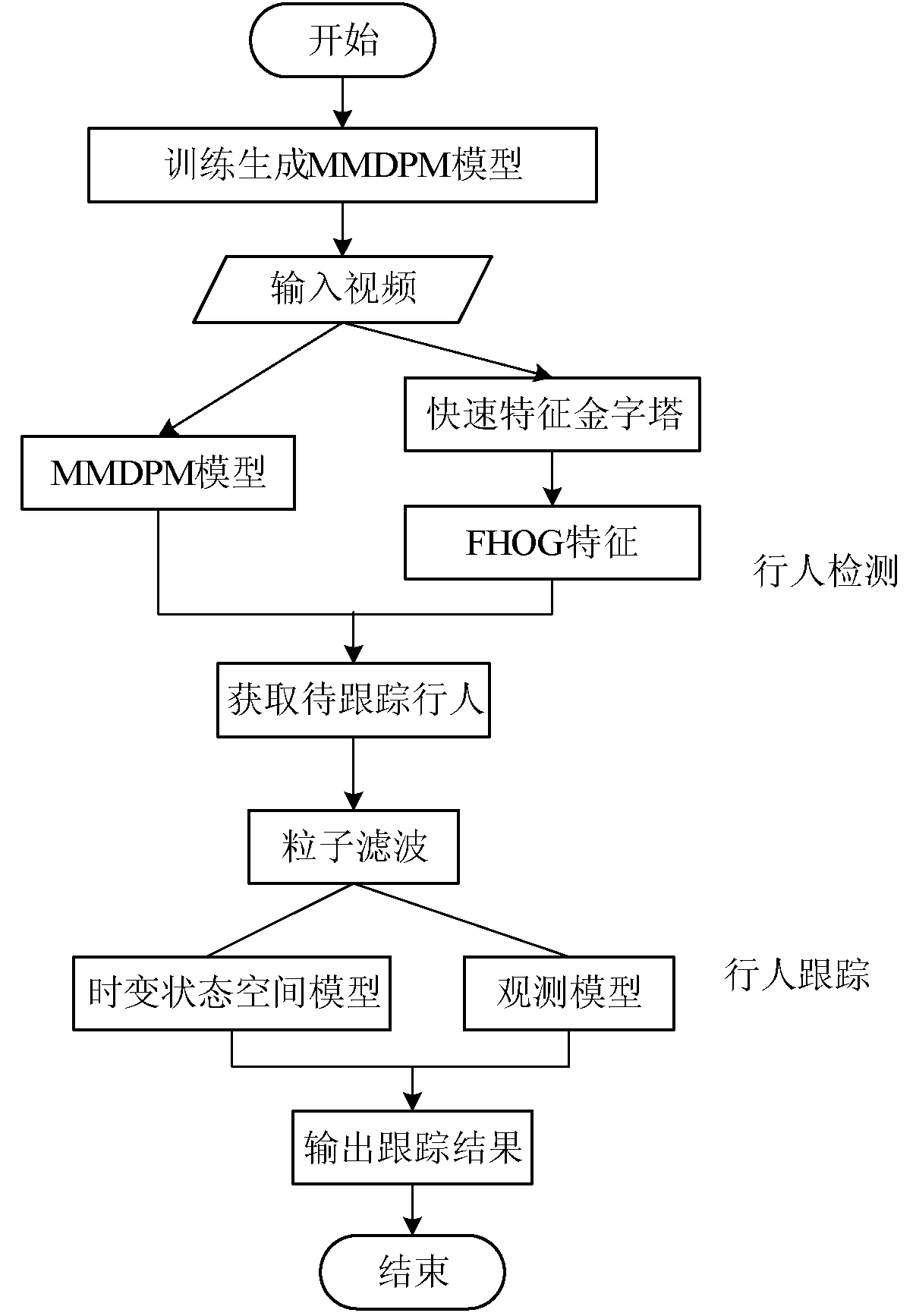
图4 行人跟踪算法框架
3 实验结果与分析
本文基于Matlab2012b平台,选择PETSBenchmark数据集(测试长度92帧)和hockey视频序列(测试长度540帧)来进行实验。实验设计分为两部分,分别是基于快速特征金字塔的DPM行人检测,以及跟踪算法验证和实验比较。
3.1 基于快速特征金字塔的DPM行人检测
为了证明快速行人检测的有效性,将快速HOG特征金字塔应用到DPM算法中。在10个PASCAL2007分类上,用标准的HOG金字塔方法和快速特征金字塔方法(每组10个尺度,9个用近似方法得到)来测试预训练好的DPM模型。两种方法(分别用DPMs和~DPM表示)的平均查准率(AP)得分如表1所示。10个分类的平均AP分别是,DPM为37.4%,~DPM为35%。用快速HOG特征金字塔,平均AP仅仅减少了2.4%,证明了提出的方法的有效性。

表1 平均查准率得分
在PETSBenchmark数据集(前3帧)上,分别用HOG+SVM算法和基于DPM的快速算法对行人进行检测,结果对比如图5所示。其中,图5(a)中检测所用的分类器是在INRIA数据集上训练得到。通过对比效果可以看出,DPM算法的检测精度明显高于传统的方法,并且引入快速特征金字塔后,在运算量大大降低的基础上,检测性能并没有损耗,表明该检测算法具有明显的优势。

图5 行人检测结果
在PETSBenchmark数据集(413帧)上,分别计算提取传统HOG特征和快速HOG特征的时间,实验结果如表2所示。通过对比可以看出,在相同的运行环境下,提取FHOG特征的时间是提取HOG特征的时间的5.2倍。由此表明本文的快速算法大大降低了运算量,降低了检测时间。
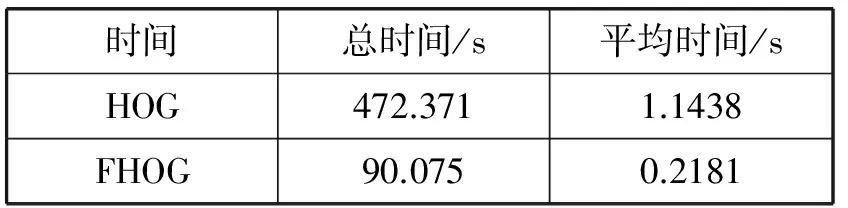
表2 本文特征与传统特征的提取时间
3.2 改进跟踪算法与传统算法的比较
在PETSBenchmark数据集上,分别用本文跟踪算法(基于时变状态空间模型和基于颜色梯度方向直方图的观测模型 的粒子滤波跟踪算法)、基于时变状态空间模型的粒子滤波跟踪算法和传统跟踪算法三种跟踪算法对行人跟踪进行实验,结果对比如图6所示。其中,粒子集N=100,各图中第一行依次为第1、15、42帧,第二行依次为第64、78、91帧,红色框为概率最大的粒子框,即跟踪结果。

图6 PETS数据集部分单人跟踪结果
通过对比效果可以看出,从第15帧开始,传统跟踪算法和基于时变状态空间模型的粒子滤波跟踪算法虽然可以定位行人的大体位置,但是匹配精度开始下降。由于本文算法的观测模型采用颜色梯度直方图对行人建模,不仅包含传统方法的颜色信息,还加入了行人的空间信息和纹理信息,因此可以准确地跟踪行人。即使行人被短时的部分遮挡后,也能迅速地锁定跟踪行人。
因为PETS Benchmark数据集中的行人运动速度相对稳定,所以,基于时变状态空间模型的粒子滤波跟踪算法和传统算法相比,并没有体现其优越性。因此,为了进一步验证改进跟踪算法的有效性,选择行人目标运动速度变化比较大的hockey视频做实验,跟踪结果对比如图7所示。其中,第一行依次为第38、93、183帧,第二行依次为第260、389、500帧。通过对比效果可以看出基于时变状态空间模型的粒子滤波跟踪算法可以较准确地定位行人的位置,但是匹配精度较低;本文跟踪算法在准确定位行人位置的同时,采用基于颜色梯度方向直方图的观测模型,匹配精度提高,因此可以跟踪非匀速运动的行人目标。此外,该视频序列中存在相同的人体外表和服饰,说明该算法在跟踪目标的外表干扰下也能较好地跟踪行人。

图7 hockey视频序列部分单人跟踪结果
在PETS数据集和hockery视频序列中,三种算法跟踪结果的平均均方根误差如表3所示。可以看出本文跟踪算法的平均均方根误差较小,具有较好的跟踪精度。

表3 平均均方根误差
4 结 语
对于非线性、非高斯分布的视频序列跟踪,本文选择基于粒子滤波原理的跟踪方法。其中,在检测行人时,为了解决制约检测算法的实时性和行人的非刚体性等问题算法,在混合多尺度DPM基础上,采用快速特征金字塔计算行人特征,加速多尺度特征的计算;在跟踪行人时,为了克服粒子传播的盲目性,提高粒子集的使用效率,采用时变的状态空间模型适应行人不同的运动状况变化,同时观测模型采用颜色梯度直方图对行人建模。实验证明,改进后的检测算法和跟踪算法提高了行人的检测准确率和跟踪鲁棒性。下一步将主要研究在提高跟踪算法的鲁棒性的同时,提高算法的实时性,使其满足复杂环境下的实时行人跟踪。
[1] Felzenszwalb P F, Girshick R B, McAllester D, et al. Object detection with discriminatively trained part-based models[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2010, 32(9): 1627-1645.
[2] Dollár P, Appel R, Belongie S, et al. Fast feature pyramids for object detection[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2014, 36(8): 1532-1545.
[3] Tang S, Andriluka M, Schiele B. Detection and tracking of occluded people[J]. International Journal of Computer Vision, 2014, 110(1): 58-69.
[4] Shenoy A V, Prakash J, Prasad V, et al. Practical issues in state estimation using particle filters: Case studies with polymer reactors[J]. Journal of Process Control, 2013, 23(2): 120-131.
[5] Hess R, Fern A. Discriminatively trained particle filters for complex multi-object tracking[C]//Computer Vision and Pattern Recognition, 2009 IEEE Conference on. IEEE, 2009: 240-247.
[6] Hu Y, Baraldi P, Maio F D, et al. A particle filtering and kernel smoothing-based approach for new design component prognostics[J]. Reliability Engineering & System Safety, 2015, 134: 19-31.
[7] Yin S, Zhu X. Intelligent particle filter and its application on fault detection of nonlinear system[J]. IEEE Transactions on Industrial Electronics, 2015, 62(6): 3852-3861.
[8] Dalal N, Triggs B. Histograms of oriented gradients for human detection[C]//IEEE Computer Society Conference on Computer Vision and Pattern Recognition. IEEE, 2005, 1: 886-893.
[9] Dollár P, Wojek C, Schiele B, et al. Pedestrian detection: An evaluation of the state of the art[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2012, 34(4): 743-761.
[10] Sonka M, Hlavac V, Boyle R. Image processing, analysis, and machine vision[M]. 4th edition. USA: Cengage Learning, 2014.
[11] Khan Z H, Gu I Y H. Online domain-shift learning and object tracking based on nonlinear dynamic models and particle filters on Riemannian manifolds[J]. Computer Vision and Image Understanding, 2014, 125: 97-114.
[12] Bera A, Galoppo N, Sharlet D, et al. Adapt: real-time adaptive pedestrian tracking for crowded scenes[C]//Robotics and Automation (ICRA), 2014 IEEE International Conference on. IEEE, 2014: 1801-1808.
[13] Li K, Feng R. Multiple feature fusion video pedestrian tracking algorithm based on particle filter[J]. Computer Engineering, 2012, 38(24): 141-145.
[14] Li H, Xiong S, Duan P, et al. Multitarget tracking of pedestrians in video sequences based on particle filters[J]. Advances in Multimedia, 2012, 2012: 1-14.
RAPID PARTICLE FILTER PEDESTRIAN DETECTION AND TRACKING BASED ONDEFORMABLE PART MODELS
Wang Chuanxu Hao Yanting
(CollegeofInformationScienceandTechnology,QingdaoUniversityofScienceandTechnology,Qingdao266061,Shandong,China)
Aiming at the problem of pedestrian detection and tracking, a new fast pedestrian detection based on deformable part models and an improved tracking algorithm based on particle filter are proposed. In the pedestrian detection stage, the mixtures of multiscale deformable part models is adopted to improve the detection accuracy of non-rigid pedestrian; meanwhile, the fast feature pyramids based on the prediction algorithm is adopted to reduce the computing time of multi-scale pedestrian features instead of traditional calculation of each scale characteristics of the pyramid. In the pedestrian tracking stage, the state space model of time-varying and the observation model based on color gradient histogram are used to track the pedestrian. Experiments show that the modified pedestrian detection algorithm yields considerable speedups with negligible loss in detection accuracy, and the modified particle filter algorithm can achieve a better tracking for the non-rigid pedestrian compared with the traditional pedestrian tracking.
Pedestrian detection Pedestrian tracking Deformable part models Fast feature pyramids Particle filter
2015-12-28。国家自然科学基金项目(61472196);山东省自然科学基金项目(ZR2015FM012)。王传旭,教授,主研领域:图像处理,计算机视觉。郝艳婷,硕士生。
TP391
A
10.3969/j.issn.1000-386x.2017.01.029

