考虑流固耦合作用桨毂形状对螺旋桨性能影响研究
邹 劲 许 杰 孙寒冰 任 振
(哈尔滨工程大学 船舶工程学院 哈尔滨150001)
考虑流固耦合作用桨毂形状对螺旋桨性能影响研究
邹 劲 许 杰 孙寒冰 任 振
(哈尔滨工程大学 船舶工程学院 哈尔滨150001)
基于STAR CCM+和ABAQUS软件,运用平均雷诺方程和SST k-ω湍流模型,建立一种基于流固耦合、可有效预报全浸螺旋桨水动力特性的数值计算方法。以标准模型DTMB P4381为网格验证对象,并对不同桨毂形状下的DTMB P4381水动力特性进行双向流固耦合计算,探讨圆柱形桨毂与球形桨毂对该无侧斜桨性能影响及作用机理。结果表明:考虑流固耦合作用能更准确预报螺旋桨水动力性能;桨毂形状对桨叶根部的流动影响明显,对桨叶表面压力分布的影响可延伸至0.5倍半径处,并且该影响随着进速系数的增大而增大。
螺旋桨;流固耦合;球形桨毂;圆柱形桨毂
引 言
针对螺旋桨水动力性能的数值模拟计算技术已经日趋成熟,在以往的一 些文献中,也探讨了湍流模型、Y+值以及网格类型的选取对数值模拟精度的影响[1-4]。此外,Young Y L[5-6]基于三维势流理论采用边界元法结合有限元法对复合材料螺旋桨进行流固耦合计算,较好地模拟了复合材料的变形,但基于无粘假设终究无法真实模拟流场运动。张帅等人[7]采用弱耦合的方法对某系列螺旋桨进行流固耦合运算。桨叶的变形改变了其表面的压力分布并引起螺旋桨周围流场的变化,桨叶变形前后的推力系数最大相差9.3%,扭矩系数最大相差8.1%,桨叶变形引起螺旋桨敞水性能的改变不可忽略。任弘等人[8]在ANSYS Workbench仿真环境中,分别运用单向流固耦合和双向流固耦合方法对螺旋桨静变形量进行计算分析和比较。采用双向流固耦合方法所得出的桨叶表面正、负压力峰值均升高, 分布较单向流固耦合更均匀。
不过,目前国内对于在流固耦合作用下,桨毂形状对螺旋桨性能影响的研究尚未涉及。
事实上,桨毂形状的改变成本较低,但对优化螺旋桨周围绕流场却具有一定的积极作用。因此,开展桨毂形状对螺旋桨性能的影响机理研究具有重要的实际意义。尹超等人[9]通过大型轴流风机出口的轮毂形状对风机的特性影响研究,发现风机出口轮毂形状的变化对该风机叶尖流场结构影响很小。当风机出口无轮毂时,在叶根区域出现了约占20%叶高区域的分离流,大大降低了工作效率;在相同的叶尖间隙下,风机效率随着出口轮毂扩压角减小而提高。王超等人[10]通过对常规螺旋桨桨毂末端加装毂帽鳍来研究其对螺旋桨性能的影响规律。鳍的存在改变了桨毂处水流的速度分布,使原先围绕桨毂随螺旋桨方向旋转的水流沿着鳍向桨后运动而不在桨毂处汇集,从而减弱了桨毂涡流。
本文针对以上问题,基于流体计算软件STAR CCM+和有限元软件ABAQUS,建立船用全浸螺旋桨流固耦合计算方法,以DTMB P4381[11]螺旋桨为研究对象,深入探讨桨毂形状对桨性能的影响规律及作用机理。
1 数值计算方法
1.1 流固耦合计算方法
本文基于STAR CCM+和ABAQUS平台对螺旋桨进行流固耦合计算:基于STAR CCM+求解N-S方程,得到水动力预报值;并且通过编译INP文件,将水动力预报值传递到ABAQUS中计算产生的应力及变形,再将收敛的变形值传递回STAR CCM+,如此反复直至计算收敛。具体计算流程见图1。
根据流固耦合所遵循的守恒原则,在流固耦合交界面上,流体域和固体域之间相互传递的应力τ 与位移d等变量应当是守恒的,即:
式中:下标f表示描述流体域的变量;下标s表示描述固体域的变量。
其中,三维粘性湍流流体的连续性方程和基于RANS的动量方程可以表示为:
式中:P为静态压力,Pa;μ为湍流粘度;ρ为液体密度,kg/m3;δij为克罗内克符号;为未知的雷诺应力项,Pa。需要湍流模型对动量方程进行封闭。本文选用SST k-ω湍流模型,因为该模型在近壁区采用k-ω方程,在其他区域则采用k-ε方程以获得湍流粘性作用。这样不仅考虑到了k-ω方程近壁区模拟时的有效性,也考虑到远场区无法准确模拟的不足。
在ABAQUS中计算由水动力产生的变形,求解瞬态动力学方程:
式中:M为质量矩阵,由密度和外形决定;Mh为水动附加质量矩阵;K为刚度矩阵;D为阻尼矩阵,由M和K决定;Dh为水动附加阻尼矩阵;Fce为旋转所产生的离心力,N;Fco为惯性力,当小变形时可忽略不计,N;Fh为水动力载荷,N;u为位移,m。
本文不考虑金属螺旋桨的阻尼特性。
1.2 计算模型
本文以无侧斜常规桨DTMB P4381为研究对象,以DTMB P4381桨作为标准桨模,相关试验及理论研究均较为成熟,可有效验证数值方法的精度。该桨的主要几何参数和材料属性参数见表1。

表1 DTMB P4381桨几何参数与材料属性参数
1.3 边界条件及网格方案
为精确获取螺旋桨周围流场的信息,避免流场变化平缓区域的计算资源浪费,故对整个计算域进行分区网格划分。取直径为5D、长度为11.5D的圆柱体为静止域,同时建立直径为1.2D、长度为0.85D的小圆柱体作为旋转域(如图2所示)。
在STAR CCM+中,运用多重参考系MRF,配合变形网格Morphing运动方法来实现桨叶的变形运动模拟,通过调节时间步长实现瞬态计算。旋转域设定动参考系绕X轴旋转。进口设置为速度入口,给定相应进速系数下的均匀来流速度;出口设置为压力出口边界;圆柱体侧面设置为对称面以模拟无穷域;桨叶及桨毂壁面设置为无滑移固壁。
Y+值是第一层网格质心距离壁面的无量纲距离,不同的湍流模型对Y+值的要求也不同。对于SST k-ω模型,螺旋桨计算理论上最合适的Y+值范围在30~300[12]。本文选取的Y+值为40,在沿着桨叶表面外法向共划分5层边界层网格,最内层尺寸为0.114 mm。
采用切割体网格对柱形桨毂DTMB P4381螺旋桨的计算域进行离散,旋转域近壁面采用棱柱层网格以捕捉边界层内部流动细节,在螺旋桨导边、随边、叶根和桨毂处进行加密处理。保持边界层网格尺寸及形式不变,选择5.7‰D、4.6‰D和2.3‰D这三种基本网格尺寸对桨叶划分网格(此处不考虑流固耦合作用),验证计算结果对网格数量的依赖性。三种网格方案如图3所示。
在均匀来流下,螺旋桨的水动力性能计算需要监控的水动力系数为[13]:
式中:KT为推力系数;T为推力,N;KQ为扭矩系数;Q为扭矩,N·m;η为效率值;J为进速系数。DTMB P4381螺旋桨的水动力系数结果及计算误差结果见表2。

表2 网格数量相关性验证
将不同网格方案的数值计算结果与试验值作对比,可看出在低速度段,三套网格都能保证一定精度。然而随着进速系数增大,第一套网格就暴露出由于网格数量较少而无法较好捕捉流场细节的缺陷。当进速系数为0.9时,效率误差达到-6.732%。第三套网格由于网格数量过多,网格计算残差不断积累而导致高速段计算误差不断增大。当进速系数为0.9时,效率误差达到-6.452%。第二套网格数量适中,既能较好地捕捉流场细节,也不会因计算残差积累而导致计算误差变大,全速段误差最大不超过5%。因此,综合考虑计算精度及成本,最终选择第二套网格方案。
在ABAQUS中,只对桨叶划分网格以减少网格数。由于桨叶是高度不规则曲面,所以采用自由划分的二阶四面体网格C3D10,在桨叶导边、随边及叶根处适当加密。设定桨叶面为交界面,桨叶根为固支边界条件,施加相应转速下的离心力。将稳态计算的流场作为双向流固耦合计算的初场,有利于加速计算收敛。图4为结构网格划分示意图。
1.4 流固耦合计算方法验证
运用已经建立的螺旋桨流固耦合计算方法,对柱形桨毂DTMB P4381螺旋桨进行全速段双向流固耦合计算,并将考虑结构变形后的水动力系数与试验值进行比较,计算结果及误差如表3所示。
从表3可见:考虑流固耦合作用时,在一定程度上更能真实模拟试验现象。流固耦合计算结果误差为3%~4%,计算精度优于没有考虑流固耦合作用的单纯水动力计算结果,船用全浸深螺旋桨的结构变形对性能的影响不能忽略不计。
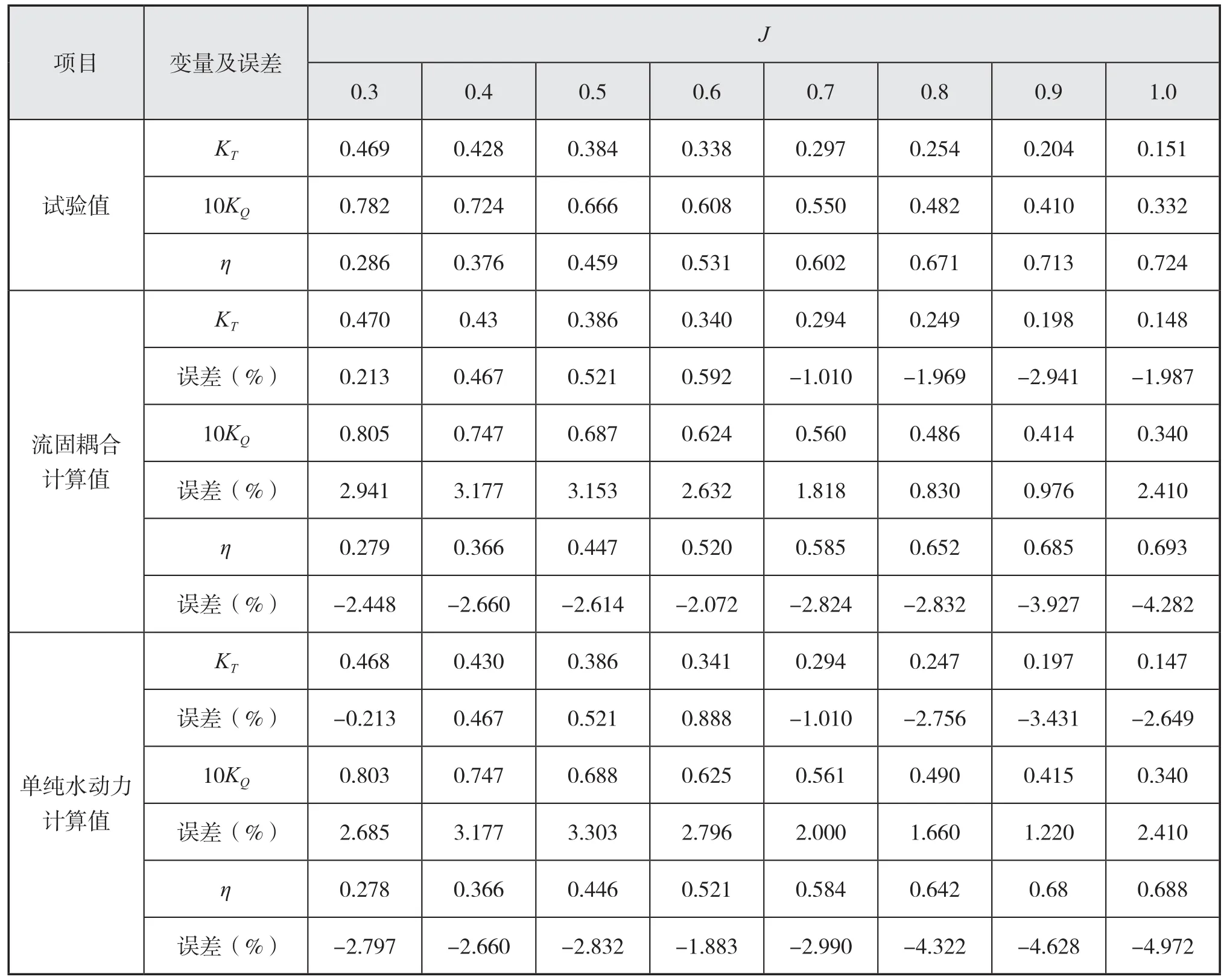
表3 试验值与计算值对比
2 两种桨毂计算结果对比分析
球形桨毂在来流方向上的形状是一个类似椭圆形的延伸体,去流方向段同上延伸至计算域。为加强可比性,本文将球形桨毂的直径设置为与柱形桨毂的直径相等,这也是此次桨毂形状对桨性能影响研究的关键。同样采用基本网格尺寸为4.6‰D,对球形桨毂螺旋桨模型进行网格划分,参见下页图5。
在ABAQUS中,也只需对球形桨毂螺旋桨桨叶进行网格划分,网格划分原则与柱形桨毂螺旋桨桨叶一致。
提取进速系数分别为0.3、0.6和1.0时的截面速度云图,对两种形状的桨毂叶根处的流动情况作对比分析,如下页图6所示,从中可以清晰看到两种桨毂在叶根处流动的差别。柱形桨毂由于桨毂在X方向上的结构不变,因此流场过渡平滑。相比于柱形桨毂,球形桨毂叶根处的流动情况更加复杂。由于其在X方向结构的变化,导致在结构突变处产生涡区,部分能量损失,所以在相同情况下,球形桨毂的效率值会低于柱形桨毂。对于球形桨毂,去流方向上的湍流涡区随着进速系数增加而向后扩大,与柱形桨毂的尾流场差别会越来越大。
图7为原点断面处径向压力分布图。对比图中不同进速系数时原点断面处的径向压力分布,可以得出:当进速系数为0.3时,叶根处的不同还不足以对整个绕流场产生重大影响,两种桨毂径向压力分布基本一致。当进速系数为0.6时,不可忽略叶根形状的不同。球形桨毂叶根处已出现低压区,对整个绕流场影响增大。当进速系数为1.0时,可以很明显看出两者不同——柱形桨毂低压区大概在距原点3/4半径处且绕流场均匀,而球形桨毂低压区则慢慢向叶根靠近时,叶根处流动的不确定性将导致绕流场不再似低速时那么均匀。
螺旋桨表面压力系数计算公式[14]见式(6):
式中:P为静压,Pa;P0为参考压力,取一个大气压力,Pa;VA为来流速度,m/s;n为转速,取10 r/s; R为半径,m。
由该式可计算得到当进速系数分别为0.3、0.6和1.0时,某一位置桨叶在0.35R和0.5R处的弦向压力系数,其对比见图8。
从图8可以看出,由于桨毂形状的不同所导致的桨叶根处的流动对叶表面压力的影响沿径向延伸至0.5倍半径处。同一进速系数下离叶根越近,流场影响就越大;同一半径处随着进速系数的增大,流场影响也越大。两组压力系数差别最大处出现在随边附近,这是因为球形桨毂前半段结构改变导致靠近叶根的桨叶面流速变化再经过螺旋桨旋转作用下不断积累的结果。球形桨毂桨叶表面压力系数在全速段几乎都小于柱形桨毂叶表面压力系数,说明球形桨毂螺旋桨单位时间内弦向流过的水比柱形桨毂螺旋桨流过的水更多。
3 结 论
在对螺旋桨进行数值模拟时,人们往往忽略桨毂形状对计算结果的影响。本文通过对无侧斜DTMB P4381螺旋桨的两种桨毂形状进行研究,发现桨毂形状对于螺旋桨特性的影响不仅存在,而且不可忽略。我们目前无从比较这两种桨毂的优良性,仅探讨在考虑了流固耦合作用下的两种桨毂对螺旋桨性能的影响,并得出如下结论:
(1)离散计算域网格并不是越多越精确,适量的网格数量既满足计算精度也节省计算资源。考虑流固耦合作用下的数值模拟能较好地预报水动力系数等相关参数。
(2)随着进速系数的增大,需要更精确模拟流场的真实流动情况。由于球形桨毂叶根处的流动情况比柱形桨毂变化更大,所以相同条件下,两者在高进速段的差别就越来越大。球形桨毂在结构突变处产生涡区,去流段涡区随进速系数的增加而扩大并向后延伸,都会损失部分能量。
(3)随着进速系数的增大,原点断面处径向压力分布低压区向原点靠近,叶根处流动情况相对较复杂的球形桨毂螺旋桨会引起整个绕流场的不均匀性。
(4) 与大侧斜螺旋桨相同,无侧斜螺旋桨在不同形状桨毂下的桨叶根部的流动对于整体性能的影响也不可忽略。桨毂形状的改变对桨叶表面压力分布的影响延伸至1/2半径处甚至更远,本文对此未作论述。同一进速系数下,离叶根越近对压力系数的影响就越大;同一半径处,进速系数越大对压力系数的影响也越大。
[1]何苗,王超,郭春雨,等.不同载荷工况下敞水螺旋桨尾流场的数值研究[C]//第二十三届全国水动力学研讨会暨第十届全国水动力学学术会议. 2011.
[2]郑小龙,黄胜,王超.基于CFD的螺旋桨定常水动力性能预报精度研究[J].舰船科学技术,2014(12):11-15.
[3]Morgut Mitja, Nobile Enrico. Influence of grid type and turbulence model on the numerical prediction of the flow around marine propellers working in uniform inflow[J]. Ocean Engineering,2012,42 :26-34.
[4]沈海龙,苏玉民.粘性非均匀伴流场中螺旋桨非定常水动力性能预报研究[C]//第十四届中国海洋(岸)工程学术讨论会论文集. 2009.
[5]Young Y L.Time-dependent hydroelastic analysis of cavitatingpropulsors [J]. Journal of Fluids and Structures,2007,23:269-295.
[6]Young Y L.Fluid-structure interaction analysis of flexible composite marine propellers [J]. Journal of Fluids and Structures,2008(6) : 799-818.
[7]张帅,朱锡,周振龙.易变形船舶螺旋桨流固耦合特性分析[J].海军工程大学学报,2014(1) : 48-53.
[8]任弘,李范春,杜玲. 流固耦合作用对螺旋桨强度影响的数值计算[J].武汉理工大学学报,2015(1):144-152.
[9]尹超,胡骏,屠宝锋,等. 出口轮毂形状对大型轴流风机性能影响的数值研究[J].航空动力学报,2014(5):1170-1176.
[10]王超,黄胜,常欣,等.螺旋桨毂帽鳍水动力性能数值分析[J].船海工程,2009(6):20-24.
[11]黄胜,白雪夫,孙祥杰,等. 基于流固耦合的螺旋桨水动力性能数值仿真[J].船舶,2015(1):25-30.
[12]叶剑平,庄光宇. 螺旋桨水动力性能计算粘性流体CFD方法的应用与研究[J]. 舰船科学技术,2013(4):29-34.
[13]王福军.计算流体动力学分析——CFD软件原理与应用[M].北京:清华大学出版社,2004.
[14]张帅,朱锡,侯海量.船舶螺旋桨流固耦合稳态求解算法[J].哈尔滨工程大学学报,2012(5):615-621.
E ff ect of hub geometry on propeller performance considering fl uid-structure interaction
ZOU Jin XU Jie SUN Han-bing REN Zhen
(College of Shipbuilding Engineering, Harbin Engineering University, Harbin 150001, China)
For the e ff ective prediction of the wetted propeller hydrodynamic performance, a numerical calculation method based on the fl uid-structure interaction is built by Reynolds-Averaged Navier-Stokes (RANS) equations and SST k-ω turbulence model with STAR CCM+ and ABAQUS software. Standard model DTMB P4381 has been regarded as the grid validation object. The hydrodynamic performance of DTMB P4381 with the di ff erent hub shapes are calculated under the two-way fl uid-structure interaction, and the e ff ect of cylinder hub and spherical hub on the performance of a zero-skew propeller and the operation mechanism. The results show that the propeller hydrodynamic performance can be predicted more accurately by considering the fl uid-structure interaction. It also shows that the hub shape has a great impact on the fl ow near the blade root, and the in fl uence on the blade surface pressure distribution can be extended to the half-radius and will be increased with the growing advance coeffi cient.
propeller; fl uid-structure interaction ( FSI ); spherical hub; cylinder hub
U661.31+1
A
1001-9855(2017)01-0021-08
国家自然科学基金资助项目(51509055)。
2016-10-08;
2016-10-27
邹 劲(1965-),男,博士,研究员。研究方向:高性能船整体设计与新船型开发。许 杰(1991-),男,硕士。研究方向:高性能船水动力性能。孙寒冰(1984-),女,博士,讲师。研究方向:舰船总体。任 振(1990-),男,硕士。研究方向:高性能船水动力性能。
10.19423/j.cnki.31-1561/u.2017.01.021

