基于离散Fréchet距离的地图匹配方法
郑少波, 周国祥, 张本宏, 石 雷
(合肥工业大学 计算机与信息学院,安徽 合肥 230009)
基于离散Fréchet距离的地图匹配方法
郑少波, 周国祥, 张本宏, 石 雷
(合肥工业大学 计算机与信息学院,安徽 合肥 230009)
针对离散Fréchet距离可以用于近似估计Fréchet距离且易于计算的特点,文章引入了离散Fréchet距离来判别轨迹曲线与路网路径的曲线间的距离,提出了一种基于离散Fréchet距离的全局地图匹配方法,并使用基于云模型的不确定性推理方法,实现全球定位系统(global positioning system,GPS)轨迹数据的全局地图匹配,并验证了该算法的有效性和实用性。
车辆定位;全球定位系统(GPS)轨迹数据;地图匹配;不确定性推理;规则发生器
车辆定位系统是由全球定位系统(global positioning system,GPS)和地理信息系统(geographic information system,GIS)组成,可以实现对车辆的跟踪和定位[1]。由于GPS定位精度的影响,GPS定位数据在结合数字地图的分析处理时会出现轨迹点偏离道路的现象,需要进行地图匹配,从而获得结合路网的行车轨迹[2]。
传统的地图匹配方法通常利用车辆行驶的方向与路网道路的夹角、车辆定位点到备选路段的距离长短等车辆信息来推算车辆当前的行车路段。文献[3]提出的地图匹配方法将方向、点到道路的距离等因素通过各自加权系数累加,运用权重的策略将点匹配到道路上。然而这种点到线的匹配由于缺乏对整体轨迹趋势的考虑,在复杂路网环境下的匹配容易导致误匹配。
GPS历史轨迹数据提供了车辆整体的运动趋势,目前大多数针对轨迹数据的地图匹配方法采用基于曲线相似度的全局匹配方法[4]。曲线匹配和点与线的匹配有差异,它需要使用距离准则来定义2条曲线间的相似程度[4]。文献[5]选择Fréchet距离作为路段的权重,并构建网络图,计算最短路径,最终获得最佳的匹配路段,但是Fréchet距离是考虑距离集合中的最大值,因此它很容易受到异常的影响。文献[6]使用平均Fréchet距离取代Fréchet距离用于曲线距离的评判,并利用智能云模型控制器完成地图匹配,但是其平均Fréchet距离计算量庞大,且文中未给出具体的云模型推理算法。
本文提出了一种使用离散Fréchet距离判断全局轨迹曲线和备选路径之间距离的全局地图匹配算法,离散Fréchet距离是在连续Fréchet 距离[7]的基础提出的,提供了连续测量的估计值,可以有效地用一个简单算法计算[7],简化平均Fréchet距离的计算,然后使用基于云模型的不确定性推理方法,设计路径云推理系统确定车辆实际行驶的道路,以期获得较小的时间复杂度和较高的正确匹配率。
1 离散Fréchet距离和云推理方法
1.1 离散Fréchet距离
在连续Fréchet距离的基础上,Eiter和Mannila提出了离散Fréchet距离的定义,提供了近似计算Fréchet距离的方法[7],其定义如下。
定义1 给定一个有n个至高点的多边形链P={p1,p2,…,pn},一个沿着P的k步,分割P的至高点成为k个不相交的非空子集{Pi}i=1,…,k,使得Pi=〈pni-1+1,…,pni〉,0=n0 给定2个多边形链A=〈a1,…,am〉和B=〈b1,…,bn〉,一个沿着A和B的组合步是由1个沿着A的k步{Ai}i=1,…,k和1个沿着B的k步{Bi}i=1,…,k组成,使得对于1≤i≤k,并且Ai和Bi中有1个恰好包含1个至高点[8]。1个沿着链A和B的组合步W={(Ai,Bi)}的花费为: (1) 离散Fréchet距离不足以判别曲线的相似度,因为它表示的是曲线之间关键特征点的距离,故引入定义2作为本文使用的距离。 Eiter和Mannila在文中给出了离散Fréchet距离的伪代码,并且论证了时间复杂度为O(pq)。算法使用动态规划来实现,效率非常高,不需要复杂的数据结构,可以使用离散Fréchet距离来近似地计算Fréchet距离。 1.2 云推理方法 正向云发生器是从定性信息中获得定量数据的分布情况和范围[10],以下是一维正向正态云的实现算法。 输入数据:N表示云滴数,(Ex,En,He)表示一维定性概念的数字特征。 输出数据:x表示N个云滴的定量值,u表示概念的确定度。 (1) 以En为期望值,He为均方差,生成正态随机数En′。 (2) 以Ex为期望值,En′为均方差,生成正态随机数x。 (4) (x,u)作为论域中的1个云滴。 (5) 重复步骤(1)~步骤(4)直到产生N个云滴结束。 前件云发生器的定义是对于论域里面1个确定量值x,经过正向云发生器,获得确定度u。其中u为x属于定性概念的确定度。一维前件云发生器实现算法[10]如下。 输入数据: (Ex,En,He)表示一维定性概念的数字特征,x表示定量值。 输出数据:u表示确定度。 (1) 以En为期望值,He为均方差,生成正态随机数En′。 对于确定度u∈[0,1],通过正向云发生器生成定性概念上满足确定度u的定量值x,称为后件云发生器[11]。后件云发生器实现算法[10]如下。 输入数据: (Ex,En,He)表示一维定性概念的数字特征,确定度为u,u∈[0,1]。 输出数据:x表示定量值。 (1) 以En为期望值,He为均方差,生成正态随机数En′。 本文算法按照GPS车辆轨迹采样点的定位精度构建缓冲区,获取当前车辆可能行驶的路段,按照曲线匹配距离准则计算整体车辆行车轨迹与备选路段曲线的距离,将各个距离和行车信息作为输入,用基于云模型的不确定性推理方法获取匹配度XB,实现地图匹配。算法基本步骤如下: (1) 计算当前定位点可能行驶的路段集合R。 (2) 计算R中各条可能路径与GPS轨迹路径的离散Fréchet距离。 (3) 获取车辆的当前信息,定位点与带匹配道路的距离d,定位点定位时刻行车方向与路段的正北方向角差值θ。 (4) 将上述2个信息和离散Fréchet距离带入基于云模型不确定性推理方法中获取路段的匹配度XB,根据各条路段匹配度选择车辆当前最可能行驶的路段。 2.1 备选路径集合的确定 本文采用采样误差椭圆的方法获取备选全局路段集合。假设相邻的2个轨迹点Pi和Pi+1,椭圆区域包含了2个轨迹点时间段内可能经过的所有路径,具体公式如下: (2) (3) (4) (5) 其中,vPi为轨迹点Pi处的速度;tPi为Pi处的时间,计算Pi至Pi+1所有可能的路径,得到备选路段集合R;a为所有可能路径的最大值;c为所有可能路径的最小值。 2.2 离散Fréchet距离的计算 离散Fréchet距离的计算步骤如下。 (1) 将备选路径曲线和路段曲线的至高点与至低点表示成A=〈a1,…,am〉和B=〈b1,…,bn〉,ai和bi分别为至高点和至低点,且m≤n,若n-m>5,则两曲线不相似,否则转到步骤(2)。 (2) 设曲线A至高点和至低点较少,将曲线B割分成m步,割分必须确保相同时刻的至高点和至低点相对应,设有k种划分,对于每种割分Wj={(Ai,Bi)}(1≤i≤m,1≤j≤k)。 (3) 对于每个割分,查找每步全部对应点之间的距离,找出距离中的最大值,再查找这种割分的全部步中最大距离,找出最大值[12]。 (4) 查找全部割分方法中的距离,找出最小值,当成两曲线的离散Fréchet距离。 (5) 计算得出峰谷点和峰顶点的最小离散Fréchet距离,这2个距离相减后取绝对值即为离散Fréchet距离。 2.3 三条件单规则发生器 三条件单规则发生器由三维前件云发生器与一维后件云发生器组合构成[13]。规则后件实际输出分成多种情况。三条件单规则发生器算法如下。 输入数据:前件三维定性概念的数字特征(ExA1,ExA2,ExA3)、(EnA1,EnA2,EnA3)、(HeA1,HeA2,HeA3)以及定量值(xA1,xA2,xA3),后件定性概念的数字特征(ExB,EnB,HeB)。 输出数据:满足确定度u的后件定性概念的定量值xB。 (1) 以EnA1为期望值,HeA1为均方差,生成正态随机数EnA1′。 (2) 以EnA2为期望值,HeA2为均方差,生成正态随机数EnA2′。 (3) 以EnA3为期望值,HeA3为均方差,生成正态随机数EnA3′。 (4) 计算确定度,具体公式如下: (5) 以EnB为期望值,HeB为均方差,生成正态随机数EnB′。 (7) 若是其他情况,则有: 当xA1≤ExA1,xB1计算式取负号,当xA1>ExA1,xB1取正号;xB2,xB3计算式正负号选取同理。 2.4 通过路径云推理系统确定匹配道路 本文使用的路径云推理系统实现步骤如下:获取导航定位点到候选道路的距离d、车辆行驶方向与路段方向角度差值θ以及上文所计算的离散Fréchet距离,定义路径云推理系统输入变量d、θ、离散Fréchet距离、路径云推理系统输出变量P;将路径云推理系统各变量表示为P={很小,小,中,大,很大},θ={小,中,大},d={小,中,大},离散Fréchet距离={小,中,大}。分别用云模型表示距离d中的3个定性概念为: A1=(0,10/3,0.01), A2=(10,10/3,0.01), A3=(20,10/3,0.01)。 用云模型表示其他变量的定性模型如下: B1=(0,10,0.01),B2=(30,10,0.01), B3=(60,10,0.01);C1=(0,10/3,0.01), C2=(10,10/3,0.01),C3=(20,10/3,0.01); D1=(40,5,0.01),D2=(55,5,0.01), D3=(70,5,0.01),D4=(85,5,0.01), D5=(100,5,0.01)。 三维云模型推理规则见表1所列。由表1可以看出,如果方向角度差值θ越小,定位点到候选道路的距离d越小,离散Fréchet距离越小,那么P越大。 表1 三维云模型推理规则 将输入(xA1,xA2,xA3)看成3个云滴定量值,对于27条规则,则可构造27个发生器,且均为三条件单规则。(xA1,xA2,xA3)分别作为每个发生器输入,使用三条件单规则发生器算法分别计算27条三维前件云发生器的确定度u。若确定度u>0,则此条规则被激活了;若确定度u=0,则没有激活这条规则。 (6) 其中,M为激活的规则的数目。 xB即为所求的综合匹配度,xB越大则该备选路径与所行驶的路段匹配度越高,至此可以得到匹配的路段。 为了测试该算法在实际应用中的效果,本文使用合肥协力公司2015年3月28日提供的GPS车辆定位数据,采样间隔为30 s,车辆经过明珠路-集贤路-芦花路-石楠路-铭传路-香樟大道,路网数据采用合肥市城市路网数据。文中以相邻采样点作误差椭圆获得候选道路集合,最终获得车辆当前最大概率行驶的道路。 车辆行驶轨迹如图1所示。图1中虚线上的点表示匹配之前GPS定位位置;虚线代表车辆行驶轨迹;实线表示实际匹配的道路。 图1 车辆行驶轨迹匹配效果图 由图1可以看出,在考虑了历史行车轨迹点后,车辆行车轨迹较为准确地匹配到最大可能行驶的道路上,文中算法对车辆行车路段的匹配精度有了很大提高。 本文算法与基于弱Fréchet距离全局匹配算法在时间复杂度上的结果见表2所列,其中,p表示轨迹曲线的采样点数目;q表示道路网的路径数目。 对采集到的轨迹数据进行地图匹配,统计正确匹配率,与点到线的匹配算法以及基于弱Fréchet距离全局匹配算法的匹配效果比较见表2所列。 由表2可以看出,综合考虑了历史轨迹信息和离散Fréchet距离后,匹配的总体精度获得了明显的提高。本文算法简化了弱Fréchet距离计算的同时保留了弱Fréchet距离计算曲线相似度的准确性,比传统点到线匹配算法的正确匹配率高出很多。 表2 地图匹配算法的时间复杂度和正确匹配率 本文提出了一种考虑车辆历史行车轨迹的全局匹配方法,并利用云模型的不确定性推理综合考虑了车辆的实时行车数据,使得算法的效率在时间复杂度和匹配准确性上均有所提高。通过实际数据的测试可以看出,本文算法具有实时性好、效率高、较好的匹配准确性等优点,一定程度上降低了地图匹配的误匹配率。 [1] 陶庭叶,高飞,吴兆福,等.利用高斯平滑法提取GPS观测序列中的结构振动监测信号[J].合肥工业大学学报(自然科学版),2010,33(1):106-109. [2] 陶帅,孙克文.GPS信号捕获策略的研究[J].合肥工业大学学报(自然科学版),2015,38(5):631-634. [3] YANG Jian,MENG Liqiu.Feature selection in conditional random fields for map matching of GPS trajectories[M]//Progress in Location-Based Services 2014:Lecture Notes in Geoinformation and Cartography.Switzerland:Springer International Publishing,2015:121-135. [4] 李清泉,黄练.基于GPS轨迹数据的地图匹配算法[J].测绘学报,2010,39(2):7-13. [5] YIN H B,WOLFSON O.A weight-based map-matching method in moving objects databases [C]//Proceedings of the 16th International Conference on Scientific and Statistical Database Management.Santorini Island:[s.n.],2004:437-439. [6] 曹凯,唐进君,刘汝成.基于Fréchet距离准则的智能地图匹配算法[J].计算机工程与应用,2007,43(28):223-226. [7] KENEFIC R J.Track clustering using Fréchet distance and minimum description length[J].Journal of Aerospace Information Systems,2014,11(8):512-524. [8] 朱洁,黄樟灿,彭晓琳.基于离散Fréchet距离的判别曲线相似性的算法[J].武汉大学学报(理学版),2009,55(2):227-232. [9] 朱洁,黄樟灿,彭晓琳.一种新的在线手写签名认证算法[J].计算机工程与应用,2008,44(31):178-181. [10] 陈昊,李兵.基于云模型的不确定性推理方法[J].小型微型计算机系统,2011,32(12):2449-2455. [11] 李德毅,孟海军,史雪梅.隶属云和隶属云发生器[J].计算机研究和发展,1995,32(6):16-21. [12] WYLIE T,ZHU B H.Following a curve with the discrete Fréchet distance[J].Theoretical Computer Science,2014,556:34-44. [13] PINTO A M,MOREIRA A P,COSTA P G.A localization method based on map-matching and particle swarm optimization[J].Journal of Intelligent & Robotic Systems,2015,77(2):313-326. (责任编辑 闫杏丽) A map matching algorithm based on discrete Fréchet distance ZHENG Shaobo, ZHOU Guoxiang, ZHANG Benhong, SHI Lei (School of Computer and Information, Hefei University of Technology, Hefei 230009, China) For discrete Fréchet distance can be used to approximate the Fréchet distance and has the feature of easy calculation, discrete Fréchet distance is introduced to determine the distance between the travel path curve and the curve of road network, and a novel map matching method based on discrete Fréchet distance is proposed. Finally, the global map matching for global positioning system(GPS) tracking data is implemented by using the uncertain reasoning approach based on cloud model. The effectiveness and practicality of the proposed algorithm is verified by simulation experiments. vehicle location; global positioning system(GPS) tracking data; map matching; uncertainty reasoning; rule generator 2015-12-18; 2016-02-19 国家自然科学基金资助项目(61501161) 郑少波(1991-),男,安徽六安人,合肥工业大学硕士生; 周国祥(1956-),男,安徽合肥人,合肥工业大学教授,硕士生导师. 10.3969/j.issn.1003-5060.2017.01.008 P228.4 A 1003-5060(2017)01-0042-05
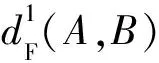
2 算法描述



3 实验结果与分析


4 结 论

