风电机组功率曲线参数模型求解方法研究

太 飞 李 飞 刘 宁 贾 斌

(1.河北建筑工程学院，河北 张家口 075400；2.中国移动通信集团河北有限公司张家口分公司，河北 张家口 075400；3.国网冀北电力有限公司张家口供电公司，河北 张家口 075400)

0 引 言

在能源与环境的双重压力下，风能作为一种优质的可再生能源逐步得到世界各国的重视.当前，中国风电经历了多年粗犷式的规模化发展后，必将走上精益化发展道路.对风电机组运行相关数据的记录和分析是实现风电场精益化运行与管理的有效途径.

风电机组功率曲线(wind turbine power curve，WTPC)精确描述了风电机组有功功率与来流风速之间的对应关系，本质上反应了风电机组的性能.WTPC是考核机组性能、评估机组发电能力、诊断机组故障和预测机组发电量的一项重要依据.风电机组制造商在向用户提供设备时，同步提供机组标准功率特性曲线，但厂家通常只提供特定温度和气压下有限对风速、功率点值M(vj,Pj).在使用功率曲线做控制或者数据分析时存在两个问题：一方面，对于风速vi若vj≤vi≤vj+1时，对应的功率需要通过曲线拟合或插值来近似获取；另一方面，当温度和气压并不是指定温度和气压时需要经过一定的换算来近似获取.由此带来的误差都会给控制与分析的结果带来不良影响.采用连续函数作为WTPC模型，并基于实测数据实时更新的WTPC模型能够有效克服上述问题，提高风电功率预测系统的精度，提高风电场精益化运行与管理程度.

粒子群优化(particle swarm optimization algorithm，PSO)算法作为一种新兴的群体智能优化技术近年来成为自然计算领域中的研究热点，并广泛应用于各类优化问题上，取得了良好的效果.类似于遗传算法，粒子群算法同样存在早熟、精度低以及易于陷入局部最优解等问题.双中心粒子群优化(double center particle swarm optimization algorithm，DCPSO)算法通过引入广义中心粒子和狭义中心粒子对粒子群算法实现了改进.

本文首先分析WTPC的五参数模型以及粒子群算法和双中心粒子群算法的基本原理.其次给出双中心粒子群算法优化WTPC五参数模型的方法.最后通过与遗传算法(GA)、PSO优化WTPC五参数模型比较证明DCPSO法优化WTPC五参数模型更具优势.

1 基本原理

1.1 WTPC五参数模型

WTPC的五参数模型即五参数逻辑方程.五参数逻辑方程是由五个未知参数确定的，一般形式如式(1)：

(1)

图1 五参数逻辑方程的逻辑曲线

式中X=(a,b,c,d,g)是一个五参数逻辑向量，a是预期的最大响应，b是斜率因子，c是曲线的中值，d是最小响应，g是不对称参数.五参数逻辑向量描述了五参数逻辑表达式形状，特定条件下的五参数逻辑向量能够使逻辑表达式的逻辑曲线如图1所示，由图可知该曲线与WTPC趋势相同.

将五参数逻辑表达式的参数作为最优化问题利用一定的算法辨识得到.目标函数如式(2)所示.

(2)

其中N为实测数据点数，Pa(i)为第i个点的实测有功功率，vi为第i个点的实测风速，Pe(X,vi)为风速vi时五参数为X时功率曲线模型的有功功率计算值.

1.2 粒子群优化算法

PSO算法模仿鸟群捕食行为，优化问题中的解被视作搜索空间中的一只鸟，即所谓的“粒子”.每个粒子均有一个由被优化函数决定的适应度，每个粒子均具有飞行速度以决定其飞行的方向和距离，然后粒子们就追随当前的最优粒子在解空间中搜索.PSO初始化为一群随机粒子(随机解)，通过迭代搜索最优解.每一次迭代，粒子依据追踪两个极值来更新自己的飞行速度，以实现更新自己的位置.首先是粒子本身搜索到的最优解，即个体极值(pbest)，其次是整个种群目前搜索到的最优解，即全局极值(gbest).PSO搜索过程的数学描述如下：

假设在一个维度为的目标搜索空间里，由M个粒子组成的初始种群X={X1,…,XM}.在t时刻，第i个粒子的位置(即最优问题的解)为Xi(t)=[Xi,1(t),Xi,2(t)…，Xi,N(t)]，速度为Vi(t)=[Vi,1(t),Vi,2(t)…,Vi,N(t)],粒子的个体极值(即粒子的最优解)为Pi(t)=[Pi,1(t),Pi,2(t)…,Pi,N(t)]；种群的全局极值(种群搜到的最优解)为Pg(t)=[Pg,1(t),Pg,2(t)…,Pg,N(t)].

由于适应度值与目标函数值对应，函数值小，适应度高.粒子的个体最好位置确定式为：

(3)

全局最好位置确定式为：

(4)

G(t)=Pg(t)=[Pg,1(t),Pg,2(t),…,Pg,N(t)],1≤g≤M

(5)

粒子群算法的更新公式为：

Vi,j(t+1)=wVi,j(t)+c1·r1,i,j(t)·(Pi,j(t)-Xi,j(t))+c2·r2,i,j(t)·(Pg,j(t)-Xi,j(t))

(6)

Xi,j(t+1)=Vi,j(t+1)+Xi,j(t)

(7)

其中，1≤i≤M，j(1,2,…,N)是粒子的第j维，w为惯性权重(inertia weight)，c1,c2为加速常数(acceleration constants)，一般取r1,i,j(t)和r2,i,j(t)为分布在(0,1)之间的随机数，t为迭代次数.

1.3 双中心粒子群算法

DCPSO的核心思想是在PSO算法基础上引入两个中心，即“广义粒子中心”和“狭义粒子中心”.广义中心粒子(General center particle，GCP)指当前粒子群中的所有个体极值的平均位置，狭义中心粒子(Special center particle，SCP)指当前粒子群中的所有个体的平均位置.两个中心粒子除了不具有速度之外，与其他粒子在本质上一样，参与个体优劣比较与全局极值的竞争.两个中心粒子与全局极值的更新公式如下：

(8)

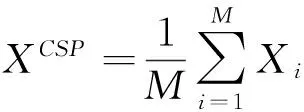
(9)

f[G(t)]=min{f[Pg(t)],f(XGCP],f[XCSP]}

(10)

2 DCPSO求解WTPC五参数模型

依据五参数逻辑方程和双中心粒子群算法的特点，本文提出采用如下步骤求解WTPC五参数模型：

Begin

Step1 搜索空间确定.依据风电机组功率曲线特征和五参数逻辑方程特性确定五参数模型参数搜索空间.

Step2 粒子群初始化.确定种群规模M，随机生成每个粒子的位置Xi和速度Vi.

Step3 适应度评价.根据式(2)评价每个粒子的适应度.

Step4 个体极值确定.根据式(3)确定每个个体的个体极值.

Step5 双中心粒子确定.根据式(8)和式(9)分别确定广义中心粒子和狭义中心粒子.

Step6 全局极值确定.根据式(4)和式(10)确定全局极值.

Step7 终止判定.如果全局极值满足问题需要或者达到最大迭代次数，则终止算法执行.否则根据式(6)和式(7)更新粒子群，执行Step2.

End

流程图如图2所示.

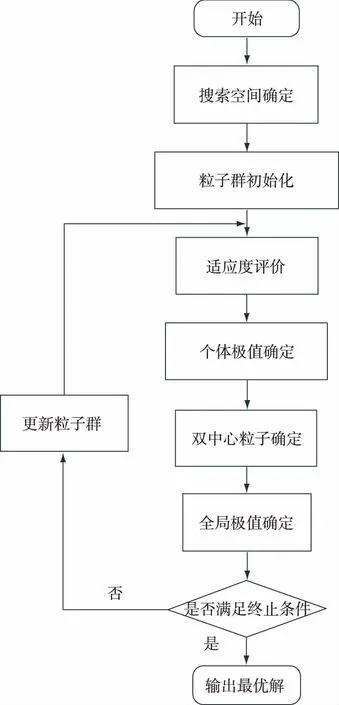
图2 DCPSO求解WTPC五参数模型流程图

3 算 例

下面通过比较GA、PSO和DCPSO算法优化WTPC五参数模型验证DCPSO求解WTPC五参数模型的优越性.实验采用的软硬件环境为：系统版本Microsoft Win7 Sp1x86旗舰版；处理器Intel(R)Core(TM)2 Duo CPU T6400主频2.0GHz；系统内存2.00GB；系统类型:32位操作系统.在Matlab R2012a语言环境下编写测试程序.为增强可比性，四种群智能算法的种群规模均为30，迭代次数均为200.GA算法中采用赌轮方法选择、交叉为单点交叉、变异采用基本位变异，交叉概率和变异概率分别为0.25和0.01.PSO与DCPSO中c1=c2=1.5，ω=1.

测试数据来源于张北地区某典型风电场SCADA系统中记录的某台具有代表性的2MW风电机组运行数据.该数据为时间序列的风速功率点值.每相邻两个点的时间间隔为10 min.将14715个数据点绘制到二维坐标的散点图如图3.

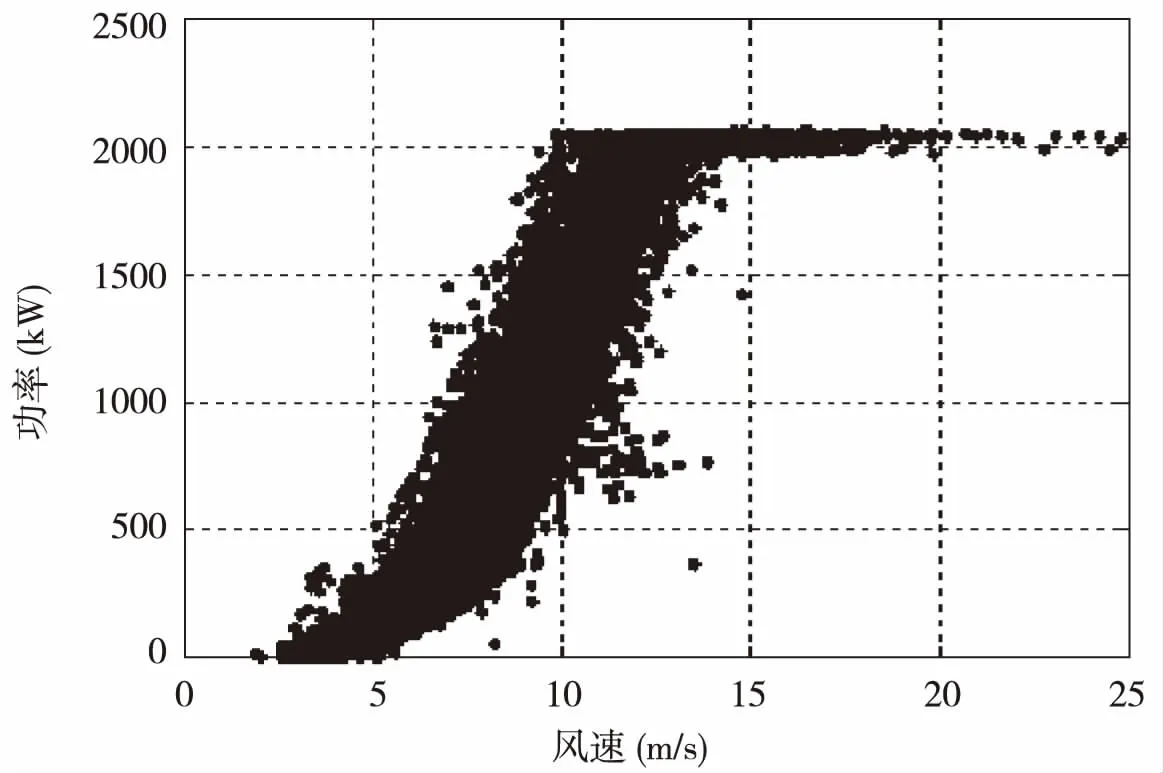
图3 测试数据散点图

采用平均绝对误差(MAE)和均方根误差(RMSE)作为结果优劣的评价指标.其中MAE、RMSE的定义如下：

(11)

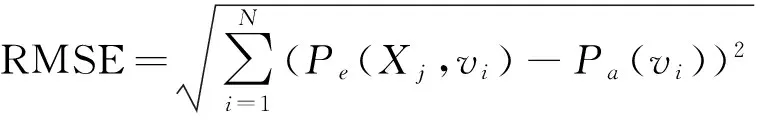
(12)

测试结果如表1和图4所示.

表1 测试结果

由表1分析可知，GA、PSO和DCPSO三种算法所求的功率曲线模型MAE和RMSE最大分别为151.31和198.60，分别为风电机组额定功率的7.6%和9.9%，具有较高的精度，因此五参数逻辑方程可以作为风电机组功率曲线的模型.GA、PSO和DCPSO优化五参数模型时，所用的CPU时间依次递增，但所求模型的MAE和RMSE逐渐递减.说明迭代200次的情况下虽然PSO算法和DCPSO比GA耗时较长，但能够求得更好的解.DCPSO比PSO耗时增加7%的条件下，所求解的精度提高了0.6%.

由表2分析可知，引入双中心后，DCPSO比PSO的收敛速度更快，如果以目标函数小于35000为计算终止条件，那么DCPSO的迭代次数明显低于PSO的迭代次数.

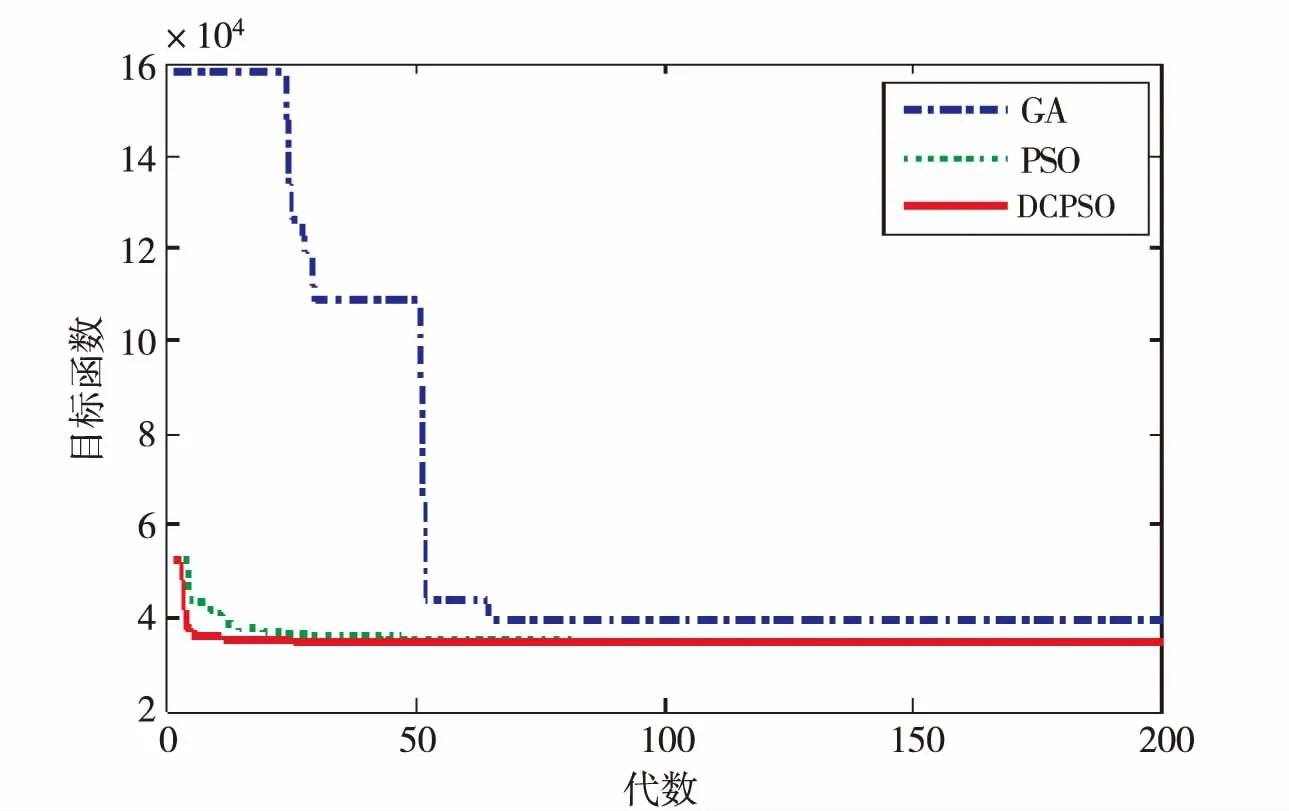
图4 三种算法下目标函数最小值变化曲线图

4 结 论

采用五参数逻辑方程作为风电机组功率曲线参数模型是有效的.双中心粒子群算法求解风电机组功率曲线时，在设定迭代次数的条件下能够求得更加精确的解，在设定模型精度的条件下能够减少迭代次数，缩短计算时间，较遗传算法和粒子群算法具有明显优势.

[1]P.G.Gottschalk，J.R.Dunn.The five parameter logistic:A characterization and comparison with the four-parameter logistic[J].Analytical Biochem.，2005，343(1)：54～65

[2]M.Lydia，A.Immanuel Selvakumar，S.Suresh Kumar，et al.Advanced algorithms for wind turbine power curve modeling[J].IEEE TRANSACTI ON SONSUSTAINABLE ENERGY，VOL.4，NO.3，JULY 2013：827～835

[3]汤可宗,柳炳祥,杨静宇等.双中心粒子群优化算法[J].计算机研究与发展,2012,49(5):1086～1094