Duffing混沌弱信号检测系统分析及电路实现

曹满婷, 宋菲菲

(燕山大学电气工程学院工业计算机控制工程河北省重点实验室，河北 秦皇岛 066004)

Duffing混沌弱信号检测系统分析及电路实现

曹满婷, 宋菲菲

(燕山大学电气工程学院工业计算机控制工程河北省重点实验室，河北 秦皇岛 066004)

采用Melnikov方法，对广泛使用的Duffing混沌弱信号检测系统进行了分析。通过Matlab软件实现了数值仿真分析，利用Multisim实现了电路仿真分析。设计制作了Duffing混沌实际电路板，通过调试得到了较为理想的检测性能。电路试验结果验证了Duffing混沌弱信号检测系统可以通过电子线路实现。该系统对Duffing混沌弱信号检测系统的实际工程应用具有促进作用，对其他混沌弱信号检测领域的进一步研究具有较高的参考价值。

Duffing系统; 混沌算法; Matlab; 抗噪性; 高斯分布; 瑞利分布; 色噪声

0 引言

当信号较微弱并且被淹没在强噪声环境中时，要提取真实的信号是相当困难的。传统微弱信号检测使用时域的方法，设备比较复杂。虽然检测方法和仪器实现技术日趋成熟，但是信噪比门限值较高、设备昂贵，这大大限制了传统微弱信号检测的应用范围。与传统弱信号检测系统相比，混沌弱信号检测系统的信噪比和检测门限可以达到更低的数量级。目前广泛使用的Duffing混沌弱信号检测系统由于很难通过电路实现，妨碍了它在弱信号检测领域的应用。为了克服上述Duffing混沌弱信号检测系统的不足，本文分析了Duffing混沌弱信号检测系统的性能，并设计、制作了相应的电路[1-6]。

1 Duffing混沌弱信号检测系统

1.1 系统性能理论分析

Duffing混沌系统是目前典型的、使用广泛的混沌弱信号检测系统。Duffing系统的基本动力学方程如下：

(1)

令a=1、b=1，则Holmes型Duffing公式为：

(2)

式中：k为阻尼比，令k=0.5；x-x3为非线性恢复力。

式(2)是一个哈密顿(Hamilton)系统，其哈密顿量表达式为：

(3)

当策动力幅值r=0时：

(4)

解得三个奇点为(0，0)、(1，0)、(1，0)。设系统的特征根为λ，系统特征方程为：

(5)

即：

λ2=1-3x2

(6)

此时，方程组可化为如下形式：

(7)

因为表达式x-x3中包含因子y，所以(0，0)为孤立奇点，也可以写成：

(8)

因为an=1、h(x)=-x2、n=1，则(0，0)的性质由n决定。因为n=1=2×0+1，则根据Briot-Bouquet引理可知：当a2×0+1>1时，奇点(0，0)为鞍点。由上述分析可知，当系统的哈密顿量h=0时，存在两条连结双曲鞍点的同宿轨道。

(9)

当策动力幅值r不为0时，系统表现出复杂的动力学形态。当r较小时，相点在两焦点附近作周期振动。随着r的增大，系统遍历同宿轨道、倍周期分岔轨道、混沌轨道；当r超过一定阈值时，系统为大周期轨道。

1.2 系统性能分析

通过相图观察及大量仿真，得出系统的策动力临界值为0.826 59。随着r的不断增大，系统相平面输出x、y经历同宿轨道、倍周期分岔、混沌状态以及大周期状态。从Duffing系统随时间变化的x、y时序图、庞加莱映射图以及随频率变化的功率谱图和随r变化的分岔图可得:系统的时序图无序，庞加莱映射图中有成片的、分形的密集离散点，功率谱连续。由此可知，Duffing系统是一个典型的二阶混沌系统。由分岔图可知，Duffing系统在随策动力幅值r逐渐增大的过程中，相点经历“周期振动-混沌-大周期”的状态。

Duffing系统弱信号检测原理是利用相轨迹分析法，观察相轨迹是否从混沌状态变为大周期状态，从而判断是否有微弱正弦信号。具体检测过程为：检测信号前，先调节幅值r，使变量x或y的输出电压为混沌波形且接近混沌到大周期的临界状态。如果外部输入同频率的弱正弦(或余弦)波电信号，之后外部输入微弱正弦波信号的幅值和r相加，使x或y输出的电压波形越过临界点。当相点从混沌波形变为大周期波形，表示检测到一个同频率的微弱正弦波信号[7-8]。

1.3 不同包络信号敏感度分析

由于实际测量中接收到的信号幅值会有一定变化，以下从指数分布、高斯分布、瑞利分布三种分布情况进行研究。幅值为指数分布的概率密度函数为：

(10)

式中：λ>0，且为常数，取λ为0.003。将系统设置为临界振荡状态，加入指数分布的同频信号，则可以看到系统由混沌状态变为大周期状态。

Duffing系统加入指数分布包络信号后的输出状态如图1所示。

图1 输出状态图

高斯分布的概率密度函数为：

(11)

式中：σ>0,σ=200;a为常数,取a=500。

高斯分布曲线如图2所示。

图2 高斯分布曲线

瑞利分布的概率密度函数为：

(12)

式中：x≥0；σ为常数，取σ=300。

瑞利分布曲线如图3所示。

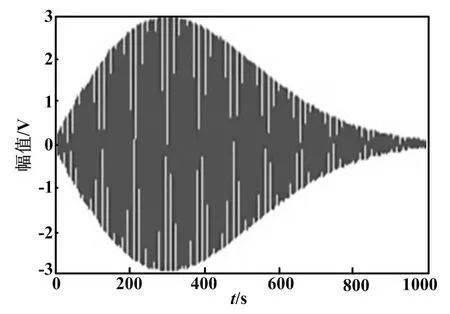
图3 瑞利分布曲线

以上分析表明：Duffing系统对弱信号极其敏感，适用于微弱信号检测。

1.4 信噪比分析

微弱信号检测的主要目的是提高信噪比。对于传统的微弱信号检测方法，如果信号频带和噪声频带重叠，则在抑制噪声的同时将不可避免地损害有用信号，甚至采用窄带化技术也未必奏效。接下来分析Duffing系统的信噪比。

1.4.1 加入白噪声

先将系统设置为临界振荡状态，加入均值为0、方差为0.001的高斯白噪声，结果表明，噪声并不影响其混沌特性，只是变粗糙了。

将Duffing系统调节为临界状态，此时加入幅值为0.000 1的待测信号，同时加入均值为0、方差为10-6的高斯白噪声，结果表明，噪声并不影响其变为大周期。

1.4.2 加入色噪声

采用方差为1、均值为0的高斯白噪声，通过一个四阶带通滤波器产生高斯色噪声。

该滤波器的传递函数为：

H(z)=[0.020 1(1-2z-2+z-4)]/(1-1.637z-1+2.237z-2-1.307z-3+0.641z-4)

(13)

该滤波器的上限截止频率为0.2Hz，下限截止频率为0.15Hz(均为归一化角频率)。

高斯色噪声的功率为：

(14)

首先令噪声放大器的增益u=1，待测正弦信号放大器的增益u=0，此时只加入内部正弦信号。调节系统内置信号的幅值f=fd，此时，该系统处于混沌临界状态。

加入色噪声后，由系统的相平面轨迹图可知，系统的相轨迹仍处在混沌状态。虽然噪声比较强，但是混沌吸引子仍然能够将相点束缚在轨道内，说明混沌系统对噪声具有免疫力。当所增加的噪声强度达到一定值时，系统的相轨迹出现了毛刺，但是仍然处于混沌状态，如图4所示。使待测正弦信号增益放大器为1，调节待测正弦信号的幅值为1nV，调节高斯噪声发生器的方差，使其方差为1×10-8，此时可以观测到相平面的轨迹为大尺度周期状态，如图5所示[9]。

图4 增大色噪声的相图

图5 方差为1×10-8的相图

当输入色噪声的功率为1×10-9W时，Duffing混沌检测系统的最低检测下限为20lg(1×10-9)=-180dB，检测信噪比下限为：

(15)

混沌系统对噪声有免疫力，而对周期信号却很敏感，表现为周期信号可以使处于混沌状态的相轨迹发生变化。

2 电路实现

利用Multisim进行电路仿真，设计中所有元件均采用真实元器件型号，应尽可能使仿真结果与实际电路保持高度一致性。运算放大器选择偏置电流为2～100pA、输入失调电压为2～9mV的ADTL084，乘法器选择精确度较高的AD734，电容选择漏电小的薄膜电容[10-11]。

使用Duffing仿真电路进行试验，调节系统阈值为0.825 56。然后，加入微弱待测信号：策动力为6 366.2Hz、幅值为0.84V的正弦波，在t为6～14ms、22～36ms及40～45ms的时刻加入6 366.2Hz的0.01V正弦波。当加入待测信号后，系统变为大周期状态。经过多次调试与检测发现，加入不同频率的待测信号后，系统有时对其并不是很敏感，需要延迟一段时间后才会变为大周期。但是可以基本验证Duffing混沌系统在有弱正弦信号输入时，混沌波形由混沌态变为大周期状态，说明Duffing混沌系统具有一定的弱信号检测特性。

根据Duffing混沌仿真电路设计，后期又制作了实际Duffing混沌电路板，进一步证明Duffing混沌系统弱信号检测的可行性，对检测领域的实际应用具有一定的参考价值。

3 结束语

利用Melnikov方法，对Duffing混沌弱信号检测系统进行了理论分析。利用Matlab仿真软件，分析了Duffing系统的相平面图、时序、庞加莱、功率谱和分岔图等系统特性以及系统对指数、高斯和瑞利不同包络信号的敏感度。分析了白噪声和色噪声对系统的抗干扰性能，利用Multisim实现了电路仿真分析，设计制作了Duffing混沌电路板，并通过调试得到了较为理想的检测性能。试验结果对Duffing混沌弱信号检测系统的实际工程应用具有促进作用。

[1] 聂春燕,徐振忠.混沌系统在弱信号检测中的应用[J].传感器与微系统，2003,22(1):55-57.

[2]ZHANGXY,GUOHX,WANGBH,etal.Anewmethodfordetectinglinespectrumofshipradiatednoiseusingduffingoscillator[J].ChineseScienceBulletin,2007,52(14): 1906-1912.[3]FUYQ,WUDM,ZHANGL,etal.AcircularzonepartitionmethodforidentifyingDuffingoscillatorstatetransitionanditsapplicationtoBPSKsignaldemodulation[J].ChinaInformationSciences,2011,54(6):1274-1282.

[4] 王冠宇,陈大军,林建亚,等.Duffing振子微弱信号检测方法的统计特性研究[J].电子学报,1998,26(10):38-44.

[5] 路鹏,李月.微弱正弦信号幅值混沌检测的一种改进方案[J].电子学报,2005,33(3): 527-529.

[6] 聂春燕.混沌系统与弱信号检测[M].北京:清华大学出版社,2009.

[7] 刘海波,吴德伟,戴传金,等.基于Duffing振子的弱正弦信号检测方法研究[J].电子学报,2013,41(1):8-12.

[8] 刘海波,吴德伟,金伟,等.Duffing振子微弱信号检测方法研究[J].物理学报,2013,62(5):50-51.

[9] 聂春燕,石要武,衣文索,等.强噪声下利用混沌系统测量频率的新方法[J].传感器与微系统，2004,23(3):57-59.

[10]LIUJM.Anewwaytogeneratehighdimensionalhyperchaos[J].JournalofComputers,2013,8(9):2348-2355.

[11]许喆,刘崇新,杨韬.一种新型混沌系统的分析及电路实现[J].物理学报,2010,59(1): 131-139.

Analysis and Circuit Implementation of the Duffing Chaotic Weak Signal Detection System

CAO Manting, SONG Feifei

(Key Lab of Industrial Computer Control Engineering of Hebei Province，Yanshan University, Qinhuangdao 066004, China)

The widespread used Duffing chaotic weak signal detection system are analysed by the Melnikov method.The numerical simulation analyses are been done by Matlab software.The circuit simulation analyses are been done by using Multisim software.The Duffing chaotic circuit board is designed and producted.The ideal detection performance has been gotten through the debugging.These verify that the Duffing chaotic weak signal detection system can be realized by electronic circuit.They has a role in promoting the Duffing chaotic weak signal detection system to the actual engineering application and has the high reference value for the further research in the field of weak signal detection of other chaotic signals.

Duffing system; Chaotic algorithm; Matlab; Noise immucnity; Gaussian distrtution; Rayleigh distribustion; Colored noise

曹满婷(通信作者)，女，高级实验师,主要从事计算机控制、混沌控制相关技术的研究及应用工作。E-mail:cat@ysu.edu.cn。

TH7;TP2

A

10686/j.cnki.issn 1000-0380.201701019

修改稿收到日期:2016-06-19