基于变权重因子差分进化算法的梯级水火电力系统调度*

孙成富 赵建洋 高 磊

(1.淮阴工学院计算机与软件工程学院，淮安， 223003;2.淮阴工学院自动化学院，淮安，223003)

基于变权重因子差分进化算法的梯级水火电力系统调度*

孙成富1赵建洋1高 磊2

(1.淮阴工学院计算机与软件工程学院，淮安， 223003;2.淮阴工学院自动化学院，淮安，223003)

梯级水火电力系统的复杂性导致其调度优化问题难以使用经典的优化方法进行解决。本文通过变权重因子改进差分进化算法，提出新的方法解决其调度优化问题。采用启发式策略解决优化问题中的平衡约束。为了充分发挥能耗较低的火力发电机作用，设计基于优先列表的启发式策略，解决动态电力平衡约束。在满足平衡约束条件的过程中，部分个体的取值被改变，增加了群体的多样性，拓展了算法的搜索空间，进而得到更优的调度解决方案。仿真结果表明，本文提出的方案有效地解决了梯级水火电力系统的调度优化。

差分进化；梯级水火电力系统；变权重因子；调度优化； 启发式策略

引 言

我国经济的快速发展，需要消耗大量的电力资源。传统单纯的火力发电不仅造成煤炭资源的枯竭，还造成严重的环境污染。新能源的开发利用能够解决上述问题，并能够助力国民经济的发展。中国水资源丰富，通过水力发电，能够提供可观的电能。目前，黄河、乌江、金沙江等水电资源的开发利用，主要以梯级水电站为主。水力发电容易受河流丰枯流量的影响，造成时间空间上分布不均，因此需要水力发电和火力发电协调调度，以实现经济效益的最大化。梯级水火电力系统调度优化是电力系统调度优化研究中急需解决的课题。梯级水火电力系统的调度优化具有变量多、约束条件复杂等特点。目前，工业生产中常采用群智能优化算法解决这类复杂问题。邢英等改进遗传算法，并将其应用于双弯曲反射面天线的设计[1]；黄睿研究粒子群算法和序贯搜索算法，通过发挥它们的互补作用，提出性能较好的群智能优化算法，并利用该优化算法解决高光谱波段的选择问题[2]；张俊杰等采用蚂蚁算法解决FIR数字滤波器优化设计，提出新的算法参数配置原则，提高FIR数字滤波器的性能[3]。谷雨等将鲍威尔搜索法的局部搜索能力引入粒子群算法，提高雷达网对隐身目标的探测能力[4]。龙伟军等将遗传算法的遗传算子作为蛙跳算法的局部更新算子，提高算法的寻优能力，并将改进算法应用于雷达波形设计中[5]。

在水火电力系统的调度优化研究中，群智能优化算法得到广泛应用。文献[6]通过混沌搜索策略改进差分进化算法，提出复合优化算法，解决水火电力系统的调度优化。设计者提出的启发式搜索策略不仅解决了优化问题中的约束条件，而且还能保持群体的活性，最终得到较好的解决方案。动态压缩粒子搜索空间被提出，以改进粒子群算法。改进的优化算法用于实现短期水火电力系统的调度优化[7]。通过仿真实验，动态探索空间压缩策略提高粒子群算法的性能，并较好地解决了水火电力系统调度。为了实现水火发电机组的调度优化，文献[8,9]研究增广拉格朗日Hopfield网络法和增强排队法，并将它们进行有机结合，增强群智能算法的寻优能力，并应用于水火电力机组的调度优化。改进的多目标文化算法被用于短期水火电力系统的调度优化[10]。基于粒子群算法和蛙跳算法的混合多目标粒子群算法用于求解三峡梯级电站的防洪调度[11]。文献[12]改进梯级水电站的水火电节能发电调度策略，节能效果明显。文献[13]设计风水火长期优化调度模型，并将其转化为线性混合整数模型予以解决，得到优异的调度优化方案。分析梯级水火电力系统调度问题中的优化目标和约束条件，有针对性地改进差分进化算法，并有效解决该调度问题，计算出较优的调度方案。

1 梯级水火电力系统调度优化数学模型

该调度优化问题主要实现在满足约束条件的前提下，使整个水火电力系统达到最大的经济效益，并尽可能减少污染物的排放，保护环境。在优化过程中，需要尽可能使用水力发电机，以达到要求。

1.1 水火电力系统经济调度

该电力系统的经济调度主要考虑火力发电机消耗的燃料，并使其尽可能的少。某个火力发电机的燃料消耗为

(1)

式中：编号为i的火力发电机燃料消耗因子为asi,bsi,csi，其在时刻t的有功输出功率为Psit。

如果整个水火电力系统同时运行的火力发电机的个数为Ns，那么这些火力发电机在时间周期T内，总燃料消耗最小量的表达式为

(2)

式中：整个电力系统最小的燃料消耗量为F,单位美元($)。

1.2 水火电力系统的最小化污染物排放调度

为了实现环境保护，火力发电机需要尽量减少污染物的排放。文献[14]中给出某个火力发电机在时刻t时污染物排放量的计算方法，即有

(3)

式中：编号为i的火力发电机污染物排放量因子为αi,βi,γi,ηi和δi。

该系统最少的污染物排放量为

(4)

其中：污染物排放量为E，单位磅(lb)。

1.3 梯级水火电力系统中的约束条件

(1)动态电力平衡约束

为了保证电力系统的稳定，需要系统的电力总输出和总需求之间达到平衡,即

(5)

式中：Psit是编号i的火力发电机时刻t的有功功率输出；Phjt是编号j的水力发电机时刻t的有功功率输出如式(6)所示；PDt，PLt为电力系统时刻t的总电力需求和电力损耗。

(6)

式中：C1j,C2j,C3j,C4j,C5j和C6j为编号j的水力发电机的发电系数；Vhjt和Qhjt分别为水库j在时刻t的蓄水量和排水量。

(2)发电机有功功率输出约束

发电机有功功率输出约束为

(7)

(8)

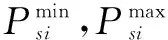
(3)水库蓄水量约束

水库蓄水量正约束为

(9)

(4)出库流量约束

出库流量约束为

(10)

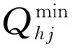
(5)梯级水库动态平衡约束

梯级水库功率平衡约束为

(11)

式中：Ihjt和Shjt分别为水库j在时刻t的进水量和溢出排水量；τmj为从水库m到j水流的时间延迟；Ruj为与水库j直接相通的上游水库数目。

2 改进差分进化算法

2.1 基本的差分进化算法

差分进化算法在执行的过程中，变异和交叉操作算子被用于改变种群中的每个个体，然后通过择优选择的方法确定足够数量的个体形成新一代的种群。

(1)变异操作 通过式(12)的变异操作算子实现种群个体的更新，即有

(12)

(2)交叉操作 交叉操作算子主要产生新一代种群的候选个体，即有

(13)

式中：第一个随机数为均匀分布于[0,1]的随机数；随机选择化问题的第q维；参数CR能够控制种群的多样性，需要预先设置。

(3)选择操作 针对最小化问题，根据式(14)进行择优选择，形成新一代的种群。

(14)

2.2 改进变异操作算子

在种群进化的过程中，种群中最优个体具有引导种群向有利方向进化的知识。为了充分利用最优个体的知识，引入改进的变异操作算子，指导种群个体的变异，即有

(15)

2.3 基于二次逼近的局部搜索操作算子

不仅种群最优个体本身包含的信息非常重要，而且该个体的局部领域内也包含重要的进化信息，能够指导种群进化。为了对最优个体的局部领域进行搜索，引入基于二次逼近的局部搜索操作算子，具体执行过程如下：

(1)确定种群中的最优个体。

(2)在种群中随机选择两个互不相同的个体b和c，并且保证它们均不同于个体a。

(3)设置维数i=1。

(4)计算

(5)如果demon为0，则变异个体Xnew的第i维的取值为个体a,b,c中随机选中个体的第i维的数值。

(6)如果demon不为0，那么Xnew的第i维取值为

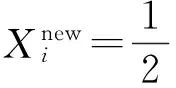
(7)i=i+1，如果i小于或等于优化问题的最大维数，那么跳转到(4)。

(8)确定新个体Xnew适应值，并进行取舍。

3 基于改进差分进化算法的梯级水火电力系统调度优化

通过分析梯级水火电力系统调度优化的数学模型可知，为了有效解决该优化问题，需要解决多目标、变量复杂和约束条件多等问题。

3.1 双目标问题转换为单目标优化问题

文献[15]中给出代价惩罚因子的方法，将梯级水火电力系统调度优化中的双目标问题转化为单目标优化问题，即

(16)

式中：修正后优化目标为TC；ht为某时间段t内使用的惩罚因子。

3.2 基于启发式策略的约束条件

3.2.1 梯级水库动态平衡约束

该优化问题中水库呈梯级状分布，它们之间蓄水量必须满足梯级水库动态平衡约束。本文通过启发式策略修正种群中的个体，使其满足该平衡约束。执行过程如下：

(1)使用变量j代表每个水库，初始化为1。

(2)在梯级水库溢出排水量为零的情况下，其动态平衡约束为

(17)

(3)在优化的时间区间中，随机确定某个时间段d，并计算Qhjd。给出计数变量num，并初始化为1。

(4)根据式(18)确定Qhjd，来达到满足开始和结束时刻梯级水库蓄水量约束条件

(18)

如果Qhjd的取值能够满足式(10)，那么转到(8)继续执行。

(5)否则根据式(19)对其进行修正。

(19)

(6)改变变量d的取值,并保证所选择的时间段没有被使用。同时递增变量num，num=num+1。

(7)若num≤T，就跳转到(4)执行。

(8)j=j+1，若j≤Nh，跳转到(2)执行。

(9)种群个体的修正过程结束。

3.2.2 动态电力平衡约束

为了充分发挥低能耗火力发电机的优势，本文在解决动态电力平衡的过程中，采用优先列表的方法。根据火力发电机在最大电力输出时的平均操作代价定义优先列表，则有

(20)

式中：某时间段t的代价惩罚因子为ht；ω1和ω2为两个不同的权重因子。

电网的平稳运行需要供给侧和需求侧保持动态平衡。种群中每个个体必须满足动态电力平衡约束，因此需要启发式策略对其进行修正，具体执行过程如下：

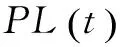
(2)初始化时间段变量t=1。

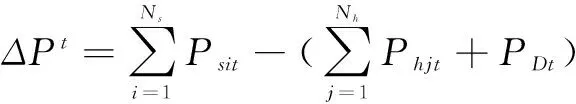
(5)若ΔPt=0，说明已经满足该约束条件，转到(14)执行；如果ΔPt<0，需要转到(10)执行。

(6)初始化计数变量m=1。

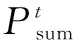
(9)m=m+1。若m≤Ns，转到(7)执行；否则转到(14)执行。

(10)重新初始化变量m=1。

(13)m=m+1。若m≤Ns，转到(11)执行。

(14)t=t+1。若t≤T，转到(3)执行。

(15)启发式的修正过程结束。

3.2.3 梯级水库的蓄水量约束

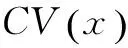
(21)

3.3 改进的梯级水火电力系统调度优化

改进的变异操作算子和二次逼近局部搜索策略能够提高差分进化算法的寻优能力，将其应用于梯级水火电力系统调度优化，能够获得较优的调度方案,优化过程如下。

(1)预设算法运行的相关参数。

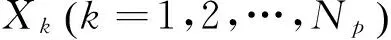
(22)

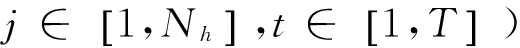
(23)

(24)

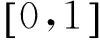
采用启发式策略修正种群中的每个个体，使它们满足梯级水火电力系统约束条件，确定每个个体的适应值。

(3)初始化迭代代数G=1。

(4)初始化种群个体下标i=1。

(8)采用代价惩罚因子，移出差的种群个体，以保证种群向好的方向进化。

(9)通过i=i+1更新变量i，若取值小于等于群体中个体的数目，转向(5)执行。

(10)应用二次逼近操作算子对最优个体的领域进行搜索，并生成新的个体Xnew。根据Xnew的适应值，以确定其是否进入种群，参与种群进化。

(11)G=G+1，若G小于或等于最大迭代次数，则转到(4)执行。

(12)得到种群中最优个体，确定梯级水火电力系统调度的解决方案。

4 仿真实验

4.1 实验环境及参数设置

将参与比较的优化算法的参数进行如下设置：基于变权重和二次逼近操作算子的差分进化算法(VWQADE)：种群规模为69，F=0.44，CR=0.85；差分进化算法(DE)：种群规模为70，F=0.44，CR=0.85；粒子群算法(PSO)：种群规模为70，惯性权重w由0.9随着迭代次数线性递减到0.4，c1=c2=2，而粒子运动的速度限制在决策变量取值范围的20%。

4.2 实验结果分析

4.2.1 梯级水火电力系统的经济调度

在梯级水火电力系统的经济调度优化中将本文提出的VWQADE算法，与粒子群算法和标准差分进化算法进行了比较，得到了这3种算法的平均燃料消耗量的收放曲线，结果如图1所示。由图1可知，VWQADE所得到的最优燃料消耗量为$41 610，而其对应的污染物排放量为30 596lb。差分进化算法和粒子群算法所得到的最优燃料消耗量分别为$42 371.00,$2 356.00，而得到对应的污染物排放量分别为 30 891.00lb和31 670.00lb。本文提出的优化算法能够得到更优的调度解决方案，算法执行的平均结果均优于比较的算法。图1给出3种优化算法所得到的平均燃料消耗量的收敛曲线。由图1可以看出。

4.2.2 梯级水火电力系统的环境调度

在梯级水火电力系统的环境调度中，差分进化算法通过执行得到的最优的污染物排放量为17 494.00lb，而其对应的燃料消耗量为$45 598.00。VWQADE所得到的最优污染物排放量为17 220.00lb，并且其对应的燃料消耗量为$45 729。粒子群算法得到更好的结果，其最优的污染物排放量为16 654.00lb，而其对应的燃料消耗量为$45 971.00。图2给出了3种优化算法执行过程中得到的污染物排放的平均变化曲线。由图2可以看出，VMQADE的性能介于粒子群算法和差分进化算法之间。

4.2.3 梯级水火电力系统的经济和环境综合调度

三种优化算法采用同样的方法将双目标优化问题转化为单目标优化问题。粒子群优化算法得到的最优燃料消耗量为MYM43 448.00，而其对应的污染物排放量18 368lb。粒子群算法得到的最优污染物排放量为18 149lb，而其对应的燃料消耗量为MYM43 675。差分进化算法所得到的最优燃料消耗量为MYM43 510，而其对应的污染物排放量为18 226lb；该优化算法得到的最优污染物排放量为17 908lb，而其对应的燃料消耗量为MYM43 522。本文提出的基于变权重和二次逼近操作算子的差分进化算法得到的最优燃料消耗量MYM43 205，而其对应的污染物排放量为17 712lb。图3给出经济和环境综合调度优化中得到的平均燃料消耗量收敛曲线；而图4给出污染物排放量的收敛曲线。由图4可知，本文提出的算法得到更优的调度解决方案，能够较好地解决梯级水火电力系统的经济和环境综合调度。

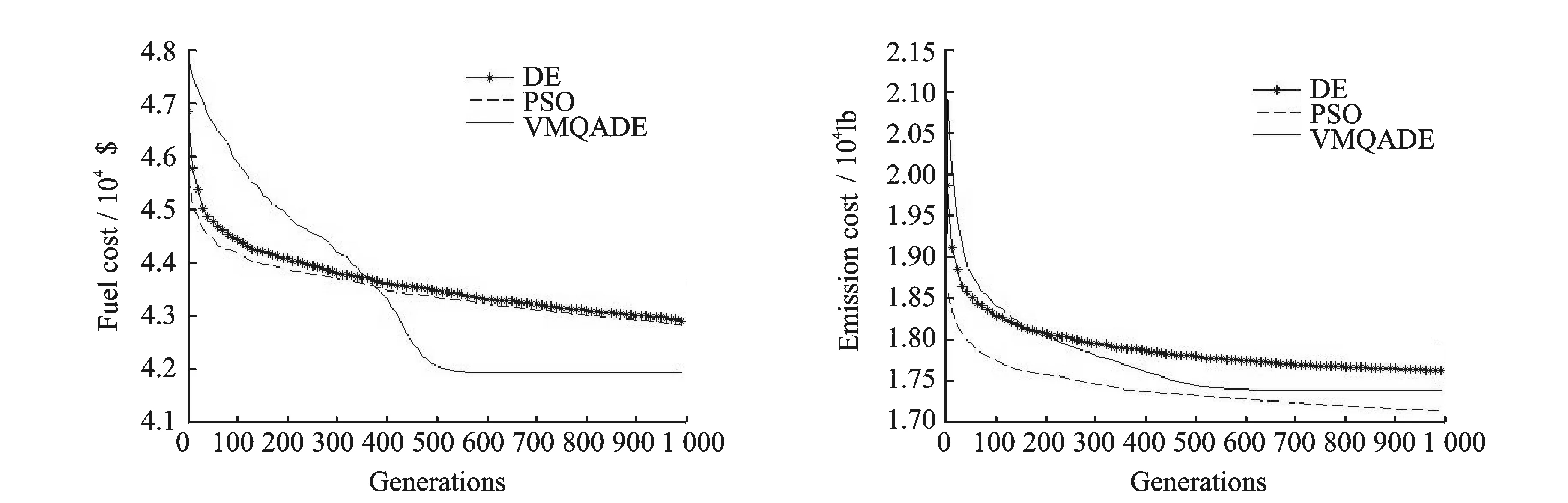
图1 ELS中平均燃料消耗收敛曲线 图2 EES中平均污染物排放量收敛曲线 Fig．1 Average fuel cost curve of ELS Fig.2 Average pollutant emission curve of EES

图3 CEES中平均燃料消耗收敛曲线 图4 CEES中平均污染物排放量收敛曲线Fig.3 Average fuel cost curve of CEES Fig.4 Average pollutant emission curve of CEES

与文献[16]相比，当进行梯级水火电力系统的经济调度优化时，VMQADE得到的最优调度解决方案能够节约$78.75/h；当进行梯级水火电力系统的环境调度优化时，VMQADE得到的最优调度解决方案能够降低43.21lb/h的污染物排放量；当进行梯级水火电力系统的经济和环境调度时，VMQADE得到的最优调度解决方案分别能够节约$71.2/h的燃料消耗和降低79.3lb/h的污染物排放量。

5 结束语

梯级水火电力系统的经济和环境综合调度优化问题是超高维的双目标优化问题。采用多目标优化算法很难得到理想的解决方案。为了有效解决该调度优化问题，本文提出基于变权重和二次逼近操作算子的差分进化算法，以得到较优的解决方案。首先，采用代价惩罚因子将该双目标优化问题转化成单目标优化问题大大降低了问题的复杂性。然后，在优化过程中通过启发式策略修正种群个体，使其满足梯级水火电力系统的各种约束条件，同时采用基于优先列表的启发式策略使能耗低的火力发电机优先进行电力输出，以达到更好的经济效益。仿真实验结果表明，本文方法能够有效地解决梯级水火电力系统的经济和环境综合调度优化问题。

[1]SelcukM,SabanO,HasanZ.SystemidentificationusingHammersteinmodeloptimizedwithdifferentialevolutionalgorithm[J].AEU-InternationalJournalofElectronicsandCommunications, 2016, 70(12):1667-1675.

[2] 黄睿, 何文勇.基于粒子群算法和序贯搜索的高光谱波段选择[J]. 数据采集与处理,2012, 27(4):469-473.

HuangRui,HeWenyong.Hyperspectralbandselectionbasedonparticleswarmoptimizationandsequentialsearch[J].JournalofDataAcquisitionandProcessing,2012, 27(4):469-473.

[3]MojtabaG,JamshidA,EbrahimA,etal.Adifferentialevolutionparticleswarmoptimizerforvarioustypesofmulti-areaeconomicdispatchproblems[J].Energy, 2016, 107: 182-195.

[4] 谷雨, 张辰璐, 李汉文, 等. 融合PSO和Powell的雷达组网反隐身部署优化算法[J]. 数据采集与处理,2016,31(3):525-531.

GuYu,ZhangChenlu,LiHanwen,etal.PSO-powell-integratedalgorithmforanti-stealthdeploymentoptimizationofnettedradar[J].JournalofDataAcquisitionandProcessing, 2016,31(3):525-531.

[5]YilmazA,ErkanB.Ageneticalgorithmsolutiontothecollaborativefilteringproblem[J].ExpertSystemswithApplications, 2016, 61:122-128.

[6]YuanXH,CaoB,YangB,etal.Hydrothermalschedulingusingchaotichybriddifferentialevolution[J].EnergyConversionandManagement, 2008, 49(12):3627-3633.

[7]HotaPK,BarisalAK,ChakrabartiR.AnimprovedPSOtechniqueforshort-termoptimalhydrothermalscheduling[J].ElectricPowerSystemsResearch, 2009, 79(7): 1047-1053.

[8]DieuVN,OngsakulW.EnhancedmeritorderandaugmentedLagrangeHopfieldnetworkforhydrothermalscheduling[J].InternationalJournalofElectricalPower&EnergySystems, 2008, 30(2):93-101.

[9]DieuVN,OngsakulW.ImprovedmeritorderandaugmentedLagrangeHopfieldnetworkforshorttermhydrothermalscheduling[J].EnergyConversionandManagement, 2009, 50(12): 3015-3023.

[10]LuYoulin,ZhouJianzhong,QinHui,etal.Ahybridmulti-objectiveculturalalgorithmforshort-termenvironment/economichydrothermalscheduling[J].EnergyConversionandManagement, 2014,52(5): 2121-2134.

[11]LiY,ZhouJ,ZhangY,etal.Novelmultiobjectiveshuffledfrogleapingalgorithmwithapplicationtoreservoirfloodcontroloperation[J].JournalofWaterResourcesPlanningandManagement, 2010, 136(2): 217-226.

[12]袁旭峰, 韩士博, 熊炜,等. 计及梯级水电站群的水火电节能调度策略[J]. 电网技术, 2014, 38(3): 616-621.

YuanXufeng,HanShibo,XiongWei,etal.Energy-savinggenerationschedulingstrategyofhydropowerandthermalpowerplantsconsideringcascadedhydropowerstations[J].PowerSystemTechnology, 2014, 38(3): 616-621.

[13]葛晓琳, 张粒子, 舒隽. 风水火系统长期优化调度方法[J]. 中国电机工程学报, 2014, 33(34): 153-161.

GeXiaolin,ZhangLizi,ShuJun.Along-termoptimalschedulingmethodforwind-hydro-thermalpowersystems[J].ProceedingsoftheCSEE,2014, 33(34): 153-161.

[14]AbidoMA.Multiobjectiveparticleswarmoptimizationforenvironmental/economicdispatchproblem[J].ElectricPowerSystemResearch, 2009, 79(7): 1105-1113.

[15]PalanichamyC,SundarBabuN.Analyticalsolutionforcombinedeconomicandemissionsdispatch[J].ElectricPowerSystemsResearch,2008, 78(7): 1129-1137.

[16]MandalKK,ChakrabortyN.Short-termcombinedeconomicemissionschedulingofhydrothermalpowersystemswithcascadedreservoirsusingdifferentialevolution[J].EnergyConversionandManagement, 2009, 50(1): 97-104.

Cascaded Hydrothermal Power System Scheduling Based on Variable Weight Differential Evolution Algorithm

Sun Chengfu， Zhao Jianyang, Gao Lei

(1.Faculty of Computer and Software Engineering, Huaiyin Institute of Technology, Huaian,223003,China;2.Faculty of Automation, Huaiyin Institute of Technology, Huaian, 223003,China)

The complexity of cascaded hydrothermal power system that its scheduling cannot be solved by the traditional method. Improved differential evolution algorithm is proposed and the scheduling problem are solved. In order to make full use of the information contained in the best individual of the population, variable weighting factor is applied to improve differential evolution algorithm, thereby the search ability of the algorithm is enhanced. The balance constraints of the scheduling problem are solved by heuristic strategy. The heuristic strategies based on priority list are devised to fully use thermal units with the lower average full-load cost and satisfy the dynamic balance constraints of power system. During the process of handling balance constraints, part of the individual’s value is changed, so that the search space is extended and the even better solutions are obtained. The simulation results show that the proposed approach can effectively solve the scheduling problem of cascaded hydrothermal power system.

differential evolution; cascaded hydrothermal power system; variable weight factor; scheduling optimization; heuristic strategy

淮安市科技支撑计划(工业)(HAG2011044, HAG2011045,HAG2013012)资助项目；淮安市重点研发计划(HAG2015034)资助项目。

2014-03-29；

2014-08-05

TP391.9

A

孙成富(1979-)，男，博士，副教授，研究方向：智能电网调度优化，E-mail:ajason509@163.com。

赵建洋(1963-)，男，博士，教授，研究方向：智能电网测控系统。

高 磊(1993-),男，硕士研究生，研究方向：智能电网自动化。