斗齿模锻过程优化设计方法研究

顾 勇， 袁鸿斌， 吴小涛

(杭州师范大学钱江学院，浙江 杭州 310036)

斗齿模锻过程优化设计方法研究

顾 勇， 袁鸿斌， 吴小涛

(杭州师范大学钱江学院，浙江 杭州 310036)

为提高模锻成形过程设计的计算效率，提出了一种基于正交设计和数值模拟相结合的优化设计方法，该方法将优化过程与有限元模拟相分离.将其应用于斗齿锻件模锻优化设计,优化了锻造过程的外形参数和工艺参数，获得了良好的效果.同时，该方法对其它模锻件成形过程的优化设计也具有指导意义.

斗齿；模锻；数值模拟；正交设计

近些年来，随着有限元技术的发展和应用，国内外学者对采用数值模拟和优化方法相结合进行锻造参数优化做了大量的工作.其中大多是以过程数学模型为基础的优化方法[1-3].这类优化设计方法能够较好地描述目标函数和变量之间的数量关系，但由于目标函数比较复杂、计算工作量大、计算效率较低等原因，一般只适用于一些简单的平面成形问题，而对于一些较为复杂的体积成形问题，这种数值模拟与优化方法耦合求解的方法计算效率将变得难以接受.所以，学者们又试图将数值模拟与优化方法进行分离求解来提高锻件成形设计的计算效率.本文提出了一种基于数值模拟和正交设计相结合的方法，用于斗齿模锻成形优化设计，从而简化优化计算过程，提高成形计算效率.

1 影响模锻成形质量的若干因素

模锻变形机理复杂，影响斗齿锻件质量的因素有很多，可以归纳为3大类，即模具因素、坯料因素和工艺因素.

1.1 模具因素

为使锻件能从模腔顺利地取出，锻件侧面上必须要有斜度.显然，模锻斜度越大，锻件越容易取出，但也增加了后续的机械加工余量，同时，模锻时金属所受到的模壁阻力也使金属充填困难.因此，通常要在保证锻件能顺利取出的前提条件下，尽量使模锻斜度取小值.

模具圆角半径对于保证金属流动、便于出模和提高锻模寿命等至关重要.模具圆角半径太大，将使得机械加工余量变大，降低了材料利用率.圆角半径太小，则金属流动不畅，模膛不易充满，还可能因此产生折迭等缺陷.

1.2 坯料因素

主要指坯料的形状尺寸.良好的坯料形状尺寸能够使金属顺利充型，并且可以降低成形载荷；相反，不合适的坯料形状往往会使坯料与模膛的适应性变差，坯料变形加剧，并且增加成形载荷，甚至发生“闷车”现象，降低了设备寿命.

1.3 工艺因素

成形工艺对模锻件质量也有较大影响.常见的可控工艺参数有摩擦因子、上模压下速度和锻造温度等.

摩擦因子对锻件最终质量很重要.不适当的摩擦会降低金属的流动性，影响锻件尺寸精度，使坯料在模具中的充填性能下降.同时，摩擦生热会破坏组织均匀性，造成锻件温度分布不合理.

对于热锻成形，模具压下速度对金属材料的流动性和充模程度有较大影响.采用较高的模具压下速度时，工件与模具的接触时间短，温度下降不多，有利于小件或厚度较小的零件的成形.同时塑性变形功还会转化为热量，使工件温度升高，模具压下速度过大则可能造成工件温度的过度上升，严重时将造成工件过烧.另一方面，模具压下速度大则工件上部运动惯性大，有利于上模的充型，这也是生产中常将工件难成形部位放在上模的原因.

锻造温度是影响坯料塑性和变形抗力的一个重要因素.当锻造温度较低时，变形抗力会增大，可锻性差.温度过高，容易导致锻件过烧、热裂纹等缺陷，浪费了能源.

课题前期研究结果表明，通过设计合理的预锻制坯形状并选择合理的工艺参数，斗齿可以经过一次预锻后终锻成形.而终锻模膛的形状主要取决于用户对斗齿形状的要求，是本课题不能过多改动的，因此本课题主要从预锻制坯形状尺寸、摩擦、模具压下速度和温度等几个方面进行研究.

2 模锻过程的优化方法

2.1 模锻过程的优化目标

模锻生产的目标应是以最低的成本和最短的时间内获得优质锻件.具体地说，理想的模锻过程，应具有以下特征：

1)锻件外形符合要求，并要节省成本.模锻过程既要保证材料充模完整，同时也要保证体积计算准确无误.这不仅可以节省材料消耗，而且可以减少后续加工工序.

2)成形载荷小.一方面可减少模具的磨损，延长模具的使用寿命；另一方面降低了设备的载荷，节省了能量，提高了设备寿命.

3)锻件具有理想的外部和内部质量.锻件的外部质量要求锻件无宏观的缺陷；内部质量要求锻件变形均匀和流线分布合理等.

上述各个特征，即为模锻过程优化设计中所要达到的目标.由于闭式模锻通常可以分成3个阶段[4]，在其形成纵向飞边阶段变形力急剧上升，这对模具寿命是极其不利的，所以本文的主要研究目标就是在不过分增大变形力的情况下尽可能使金属充满模膛，即在模膛充满度和变形力之间寻找某个合理的匹配，并尽量使应变分布均匀.显然，这是一个多目标的优化多变量的问题.

2.2 主要优化参数的确定

模锻变形复杂，坯料形状及各种工艺参数对成形结果有较大的影响，用解析法很难建立成形结果与坯料形状和工艺参数之间的对应关系.为了获得高质量的斗齿锻件，降低斗齿的生产成本，提高生产效率，有必要用基于数值模拟的方法对坯料形状及工艺参数进行优化.根据实际，本文即以预锻制坯形状、模具和工件间的摩擦因子和上模压下速度为优化设计变量来对模锻过程进行优化.

2.3 优化目标函数的建立

前文已提到模锻的控制目标是在充满模膛的条件下，满足成形载荷小、变形分布均匀.显然这是一个多目标优化问题，本文采用加权的方法来将多目标优化问题转化为单目标优化问题，即目标函数：

Ψmin=λiωi(1-V)+λjωjFmin+λk(1-ωi-ωj)Δεmin,

(1)

式中:λ是配位系数；ω是加权因子，取值范围[0,1]；V是充填度；Fmin是凸模最小载荷；Δεmin是最大应变差值.

2.4 优化目标函数系数的确定

2.4.1 加权因子的确定

在线性加权方法中，如何选择加权因子比较重要.在采用线性加权方法解决多目标优化问题时，为了消除各子目标函数在数量级上的差别，常常先将它们转化成为0～1之间的规整化子目标函数，再对其进行加权组成总的目标函数来计算数值的大小.

当目标函数经过规整化处理时，其加权因子应符合规范化权，即满足以下条件：∑ωi=1.

在应用中，加权因子的大小反映各子目标函数对整个方案的重要程度，其权值的大小可根据经验来确定.如先请多位有经验的用户对各子目标函数的重要程度进行“打分”，然后取其平均值作为对该项目目标函数的加权因子值.

本文在构造各子目标函数时，已经对目标函数进行了处理，所以在选择加权因子时，主要根据经验兼顾各子目标函数的重要性来进行确定.根据前期数据处理结果，对于整个目标充满和较小的成形载荷是主要的，因此选择加权因子ωi=ωj=0.4.

2.4.2 配位系数的确定

配位系数可将几个不同的数字统一到同一数量级上，为优化的实现提供方便.为方便计算，本文规定该统一的数量级为101.本文采用DEFORM3D软件为用户提供了直观的后处理信息，包括充填信息、载荷大小和应变值.根据前期预模拟结果，由于充填程度数值在(0，1)之间，故取λi=10；最小载荷数量级为107，故取λj=10-7；而变形过程中等效应变的值常在10以内，故取λk=1.

3 实验方案和结果

斗齿模锻是一个高温大变形过程，其变形复杂，影响因素众多，难以用解析法进行分析.为了获得斗齿成形过程中的详细信息并在此基础上对其成形过程进行优化，本文采用了数值模拟和正交试验相结合的方法.

3.1 实验模型的建立

根据斗齿锻件图[5-6]，得到斗齿模锻模具三维几何模型图，如图1所示.模拟中使用的其它计算条件如下：始锻温度为1 100 ℃；每步压下量0.425 mm；模具预热温度为300 ℃；坯料热容为418 J/(kg·K)；模具热容为352 J/(kg·K)；坯料密度为7.86 g/cm3；模具密度为9.36 g/cm3；坯料热传导系数为40 W/(m·k)；模具热传导系数23 W/(m·k)；环境温度为20 ℃.

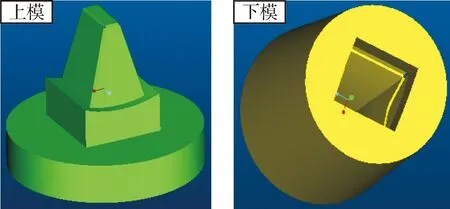
图1 斗齿模锻模具模型Fig. 1 Forging die model of bucket teeth

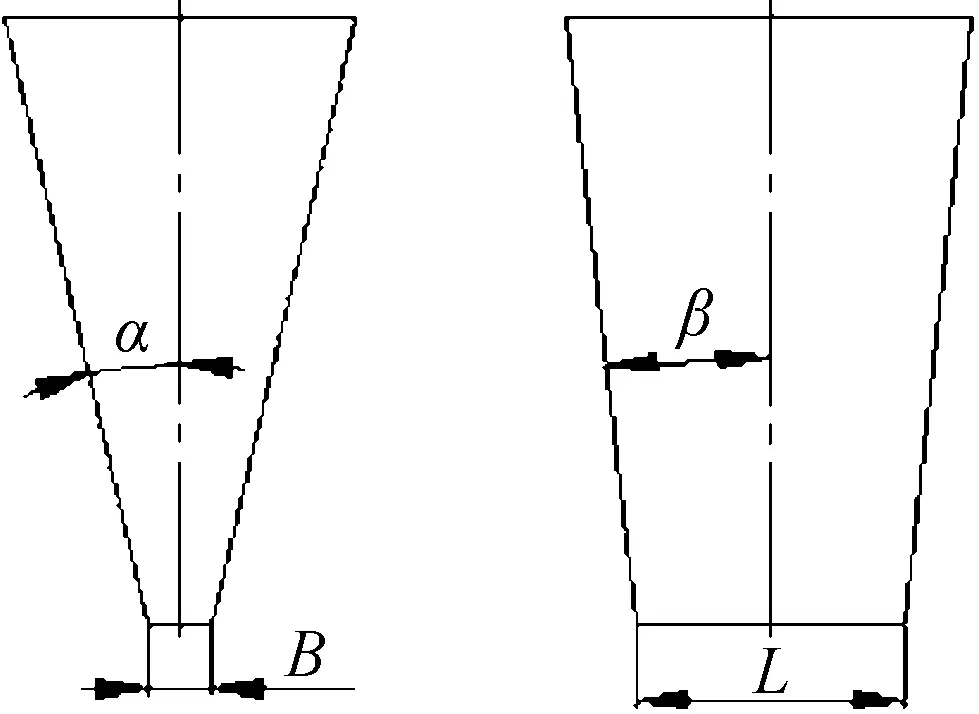
图2 预锻制坯方案Fig. 2 Pre Forging solutions

3.2 对坯料形状参数优化方案

根据斗齿锻件[5-6]形状，其预锻件宜采用对称形状，如图2所示.斗齿模锻是一个复杂的金属成形过程，属于多因素多水平问题.本文针对坯料的4个形状控制参数(α、β、B和L)给定每个因素3个水平.利用L9(34)正交实验法设计有限元模拟进行计算，对应的模拟结果见表1.依照表1结果综合分析，2号实验使得目标函数值最小，为最优方案，也即α=13°；β=4.3°；B=6 mm；L=66 mm.

3.3 对坯料工艺参数优化方案

同理,对工艺参数设计因素和水平，通过正交试验得出各个试验指标值，将各个试验指标值通过式(1)加权得到目标函数值(表2).由表2可知，在对工艺的优化过程中，3号试验目标函数值最小，即当摩擦因子m=0.2、上模速度v=80 mm/s时为最优方案.

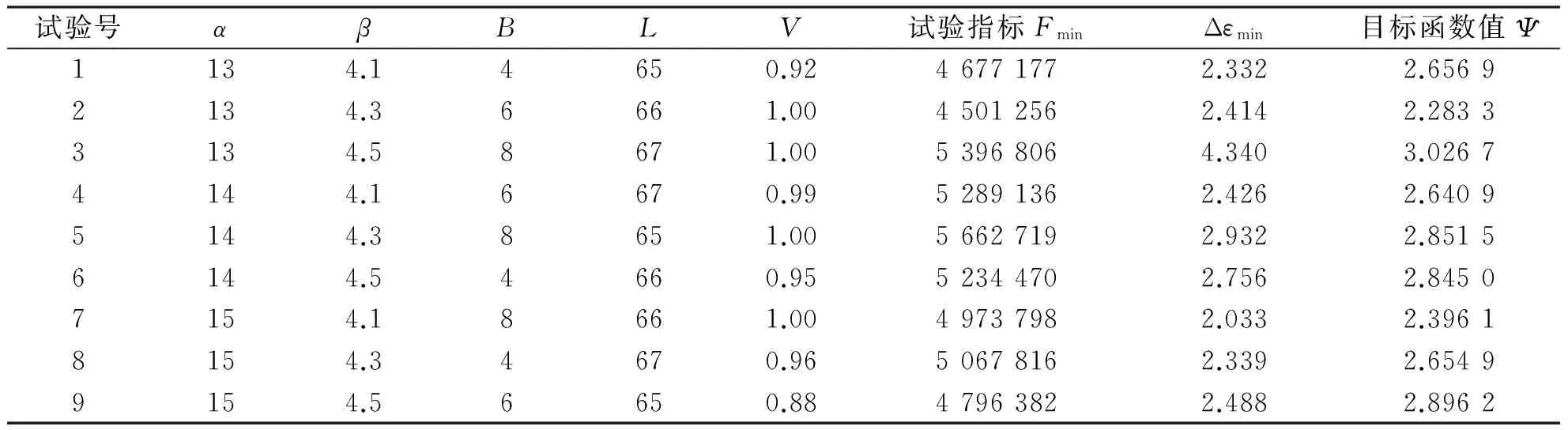
表1 外形参数实验结果Tab. 1 Experiment results of shape parameter

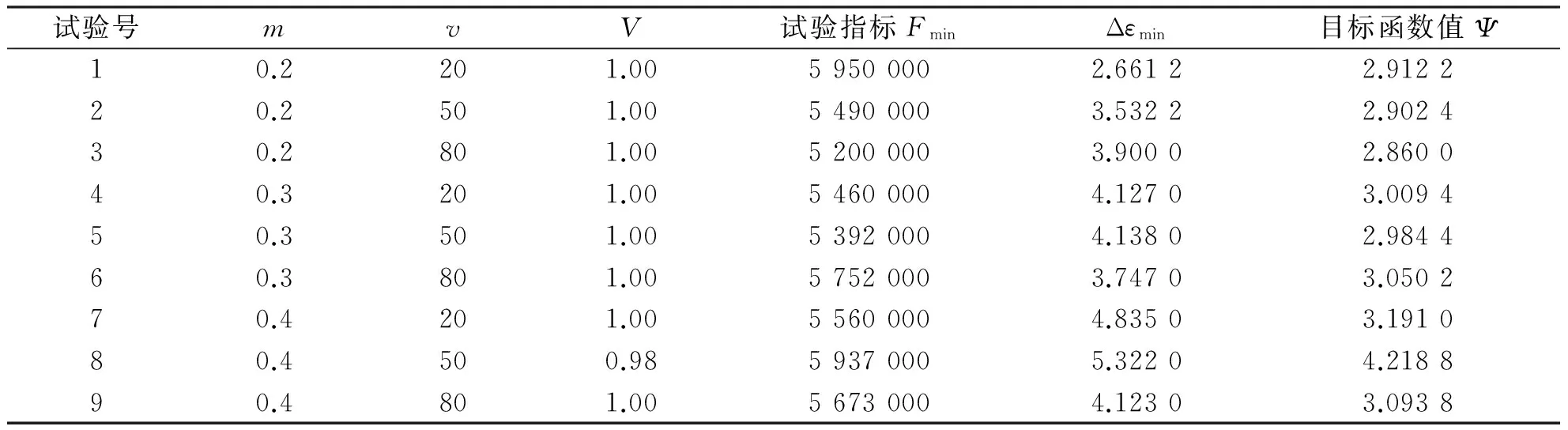
表2 工艺参实验结果Tab. 2 Experiment results of process parameter

3.4 优化结果

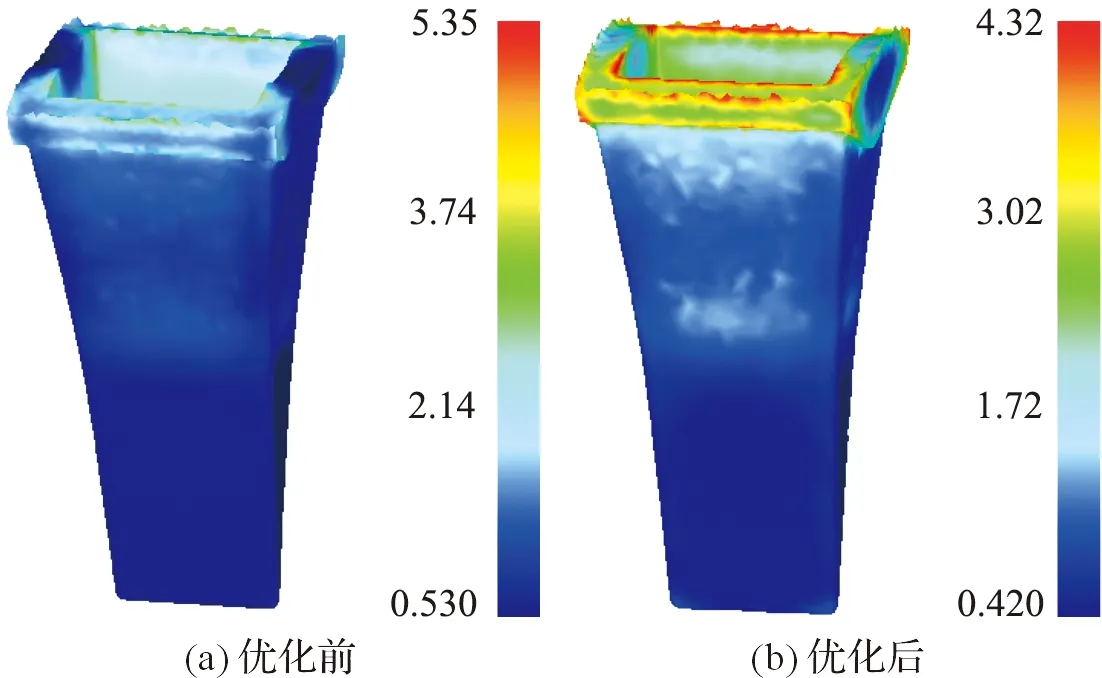
图3 优化前后的等效应变Fig. 3 Equivalent strain before and after optimization

以上的优化设计是以斗齿充填程度、成形力和变形参数为研究对象的.坯料选择形状参数为：α=13°、β=4.3°、B=6 mm、L=66 mm，工艺参数选取摩擦因子m=0.2和上模速度v=80 mm/s时，可以获得合格的锻件.综合优化后的参数，建立模型，并分析结果.

3.4.1 等效应变的比较

优化前后斗齿在成形过程中的等效应变分布如图3所示.从图中看出，整个成形过程中坯料底部都是变形的最小区域，而斗齿上部则始终是变形的最大区域.从图3(b)还可以看出，变形结束时工件应变的最大差值为3.9，比优化前要小，说明变形相对均匀，达到了优化目的.

3.4.2 成形载荷的比较

如图4所示，成形过程中随着模具不断往下运动，成形载荷逐渐增加.在变形前期和中期，由于模膛下腔尚未充满，金属的变形类似于正反复合挤压，流动阻力较小因而变形载荷上升较为缓慢，而在变形后期模膛下腔已完全充满，金属的变形转为反挤压和闭式模锻，流动阻力急剧增加，导致变形载荷急剧上升.比较优化前后载荷值，发现优化后载荷有一定下降，基本达到优化目的.

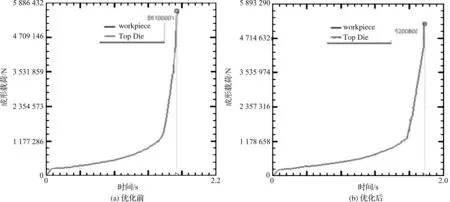
图4 优化前后的成形载荷Fig. 4 Forming load before and after optimization

4 结 论

本文分析了影响模锻成形质量的若干因素，研究了基于数值模拟的优化目标函数的构造方法，并针对模锻，给出了优化目标、设计变量及相关系数的取值.针对制坯方案，借助于正交试验方法，以充满模膛、变形载荷小及变形均匀为优化目标，得出了斗齿的合理制坯形状和工艺参数，即α=13°、β=4.3°、B=6 mm、L=66 mm、m=0.2和v=80 m/s.

[1] PARK J J, REBELO N, KOBAYASHI S. A new approach to preform design in metal forming with the finite element method[J]. International Journal of Machine Tool Design and Research,1983,23(1):71-79.

[2] GAO T, YANG H, LIU Y L. Backward tracing simulation of precision forging process for blade based on 3D FEM[J]. Transactions of Nonferrous Metals Society of China,2006,16(S2):639-644.

[3] ZHAO G Q，MA X W，ZHAO X H，et al.Studies on optimization of metal forming processes using sensitivity analysismethods [J].Journal of Materals Processing Technology，2004，147(2)：217-228.

[4] 吕炎.锻造工艺学[M].北京：机械工业出版社，1999：109-112.

[5] 顾勇，詹艳然.斗齿闭式模锻过程的工艺分析及数值模拟[J].热加工工艺，2010，39(17)：118-120.

[6] 顾勇，袁鸿斌，吴小涛.斗齿模锻数值模拟关键问题的处理及实现[J].机械制造，2016，54(2)：40-42.

Optimum Design Method for Forging Process of Bucket Teeth

GU Yong, YUAN Hongbin, WU Xiaotao

(Qianjiang College, Hangzhou Normal University, Hangzhou 310036, China)

An optimization method based on orthogonal design and numerical simulation to improve the computational efficiency die forging process design is presented in this paper. In this method, orthogonal design is employed as optimization mean, and the numerical simulation is used as computing tool. Thus, the optimization process is separated from FEM calculation. The method applies to optimum the design for bucket teeth forging, and obtained excellent optimum apparent parameters and process parameters. At the same time, the method is of great value to optimum the design for other forging blanks.

bucket teeth；forging ；numerical simulation；orthogonal design

2016-05-24

顾勇(1983—)，男，讲师，博士研究生，主要从事塑性成形工艺及模具CAD/CAE研究.E-mail：873939950@qq.com

10.3969/j.issn.1674-232X.2017.01.023

TG316

A

1674-232X(2017)01-0108-05