基于遗传算法的分布式数据库数据分配策略研究
袁 旭,孙纪敏
(中国电子科技集团公司第五十四研究所,河北 石家庄050081)
基于遗传算法的分布式数据库数据分配策略研究
袁 旭,孙纪敏
(中国电子科技集团公司第五十四研究所,河北 石家庄050081)
为进一步提升分布式数据库系统的访问效率,对数据分配问题进行分析,并结合实际应用构建出相应的数学模型。在现有以遗传算法求解该问题的研究基础上,重新优化了遗传算法,如采取选育措施得到优良初始种群、以顺序选择和最佳保存相结合的手段进行个体选择、利用大变异操作拓宽算法搜索广度等,进而提出了一种新的数据分配策略。仿真结果表明,与其他分配方法相比,运用该策略能够求得更为理想的数据分配方案。
数据分配;遗传算法;分布式数据库;数据存储
0 引言
随着企业信息化的逐步深入,业务数据高速增长、日益庞大,对数据存储的要求不断提高[1],传统集中式数据库的弊端愈加凸显。而分布式数据库则以其扩展能力强、成本优势大以及使用效果优等诸多特点[2]赢得了广阔的发展空间。分布式系统中,数据存储主要包括数据分片与数据分配两部分[3]。数据分片是指将全局数据在逻辑上划分成多个数据片段,数据分配则指的是将这些数据片段在物理上分配到系统各个工作站点上。作为分布式数据库核心设计环节,数据分配影响着系统效率和性能,是系统优化改进所需要考虑的关键性问题之一[4]。
对于数据分配问题,不同学者研究角度不同,得到的见解也不尽相同,例如文献[5-6]二者的观点也存在着差异。本文研究则面向数据处理局部性,是以减少各站点间的通信总代价为主要目标的。该方向上,有关学者给出了多种分配策略,如非冗余分配最佳适宜法、冗余分配添加副本法、启发式试消副本法[7]、基于数据片段访问特性的分配策略[8]、基于遗传算法的数据分配策略[9-11](本文称之为“GA1法”)等等。本文在GA1法的基础上进行研究,重新优化了遗传算法,提出了改良后的数据分配策略,即GA2法。
1 数据分配问题的数学模型
1.1 应用需求及问题描述
由6个位于不同城市的网络单元组成一个工作场景,每个网络单元中存在一个或多个工作站点,其内部信息交换是基于如图1所示的网络而实现的。在该工作场景的信息化建设中,很有必要采用分布式的数据存储方式。此时,数据分配问题需要充分考虑。

图1 某工作场景网络简图
结合上述,对数据分配问题描述如下:
分布式系统中存在一个存储着数据片段集F=(F1,F2,F3,F4,…,Fq)的站点集合S=(S1,S2,S3,S4,…,Sm),其各站点由计算机网络连接起来。系统内运行着检索事务集Q=(Q1,Q2,Q3,…,Qn1)和更新事务集U=(U1,U2,U3,…,Un2)。按照一定的方式将每个片段F(或副本)合理地分配到不同的站点S上能使整个系统的网络通信总代价最小,分配方案记为FAT
1.2 统计信息
实际应用中系统通信代价的影响因素纷繁庞杂,在量化研究过程中只能对相关信息进行有所依据的选取和简化处理,以降低问题的复杂性。最终采用的统计信息如下:
① 数据片段大小(size_f,行向量),体现各数据片段中的数据量;
② 访问控制信息:检索访问矩阵(rm)和更新访问矩阵(um),分别体现检索事务与更新事务(行项)对数据片段(列项)的访问需求。其中数字1表示需要访问,0表示无需访问;
③ 访问选择信息:检索选择矩阵(sel_r)和更新选择矩阵(sel_u),分别体现检索事务与更新事务的访问选择性,即不同事务(行项)对不同数据片段(列项)的数据访问量与该片段大小的百分比;
④ 事务频率信息:检索频率矩阵(freq_r)和更新频率矩阵(freq_u),分别体现各检索事务与更新事务(行项)在不同工作站点(列项)上发生的频率;
⑤ 网络传输信息:通信代价系数矩阵(delay),体现系统中单位数据于不同站点(行项、列项)之间进行传输的网络延时,且假设delay(Si,Sj)=delay(Sj,Si)。
1.3 代价公式
代价公式结合各项统计信息,建立起分配方案与其评价指标——通信代价之间的代数关系,是数学模型的重要组成部分。本文所采用的代价公式如下:
(1)
式中,sumcost为某一整体数据分配方案所对应的通信总代价;cost(Fj)为某数据片段Fj的某一分配方案所对应的通信代价,其计算公式为:
cost(Fj)=TQ(Fj)+TU(Fj),
(2)
式中,TQ(Fj)、TU(Fj)分别为数据片段Fj的分配方案所对应的检索、更新事务通信代价,其计算公式为式(3)和式(4)。
(3)
(4)
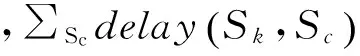
1.4 数学模型的构建与求解
在数据分配问题中,假设工作站点S的数量为m,则某片段Fj的分配方案可以用一个长度为m的二进制串结构数据来表示。若Fj被分配到站点Sk上,则该串结构数据第k个数位上的数字为1,反之为0。由此易知,片段Fj共有(2m-1)种分配方案,分别对应着不同的通信代价cost (Fj)。假设数据片段数量为q,则整个系统数据分配方案可表示为一个q行m列的0~1矩阵,共有(2m-1)q种,对应着不同的通信总代价sumcost。
数据分配问题的实质是一个典型的NP组合优化问题,其数学模型的目标函数为min(sumcost),其求解过程就是从其由(2m-1)q个q行m列的0~1矩阵组成的解空间中找出一个最优解(或满意解),即能使sumcost取最小(或近似最小)值的矩阵。
2 基于遗传算法的数据分配改良策略
遗传算法(Genetic Algorithm,GA)是一种借鉴生物界自然选择和进化机制发展起来的随机搜索技术[12-13],具有独特的算法形式与运行机理,是求解非线性复杂优化问题的有力工具[14]。此前,已有学者尝试利用遗传算法来求解数据分配问题并提出了GA1法。而本文所提出的GA2法同样基于遗传算法,宏观运算框架也与GA1法相似,仍不考虑各数据片段之间的关联,依次对数据片段集合中每一个数据片段的分配问题利用遗传算法分别求解,再进行整合得到最终的数据分配方案。但在对遗传算法的改进手法上,GA2法却有自己的特点。
现结合遗传算法运算流程,如图2所示,对某一数据片段Fj分配问题的求解过程进行简要说明。

图2 遗传算法流程图
① 设定进化参数。根据实际问题,适当设定需要预先给出的进化参数,如群体大小np,终止进化代数ng等。
② 编码成串位。将问题的解即某数据片段Fj的分配方案用二进制的串结构数据来表示,具体编码规则见1.4节。
③ 初始化群体。初始群体的特性对计算结果和计算效率均有重要影响[15]。GA2法采取选育措施来进行初始化,即:首先随机生成女排np0个个体,然后从中选取所对应通信代价最低的np个个体组成初始种群。这样操作能够在一定程度上保证初始种群中个体的优良程度。
④ 计算个体适应度值。利用式(2)、式(3)和式(4)依次求得群体中各个个体所对应的通信代价,此代价的倒数即该个体的适应度值。
⑤ 选择操作。GA2法将最优保存和顺序选择相结合来进行个体选择操作。
最优保存,当子代最优个体的适应度不及父代时,以父代最优个体取代子代最差个体,是算法收敛性的一个重要保证条件[15]。
顺序选择[16]利用个体适应度的排序将选择概率固定化,从而建立起相对稳定的选择过程,避免个别超级个体独霸种群的同时,也使得个体选择在个体间适应度相差不大的情况下仍能有效进行。其具体步骤为:首先计算群体中所有个体(数量为np)的适应度值并降序排列;再令参数p0取1/np,根据式(5)依次计算出排序后各个体(序号为j)的选择概率。
(5)
⑥ 交叉操作。为提高算法执行效率,GA2法采用简单常数概率pc下的单点交叉。
⑦ 变异操作。未成熟收敛(Premature Convergence,PC)是遗传算法中特有现象,且十分常见[15]。传统遗传算法中,为保证算法稳定性,变异概率取值通常很小,一旦出现早熟收敛,将很难跳出局部最优解。因此,GA2法采用了大变异操作[16]以便能够及时随机、独立地产生许多新个体,快速增加种群多样性,有效帮助种群脱离早熟,进而求得更为理想的解。其具体过程为:
i.判断某一代群体中个体的最大适应度fmax与平均适应度favg是否满足条件t*fmax ii.当步骤i中满足条件时,以一个比通常概率pm大5倍以上的大变异概率pmax执行变异操作,否则仍以通常概率pm执行变异操作。其中,pmax越大,算法越稳定,但这是以牺牲收敛速度为代价的。若pmax取0.5,则大变异操作就近似蜕化成了随机搜索。 另,第gen代群体经过选择、交叉、变异等操作后,得到第(gen+1)代群体。 ⑧ 判断是否满足终止准则。若当前该种群进化代数gen不大于终止进化代数ng,则转到第⑤步,继续进化。反之,若gen大于ng,则确定得到最终群体,进入第⑨步; ⑨ 解码最终群体适应度最高的个体,得到片段Fj的最优(或近似最优)分配方案。 3.1 仿真实验及运算结果 在实验中,工作站点S的数量不超过5,此时问题的解空间较小,完全能够以全遍历法直接求取最优解,采用其他方法的意义不大。因此,本文实验中的工作站点数量取值适当地增大。 结合网络场景简图1,假设有6个数据片段F、7项检索事务Q、7项更新事务U以及10个工作站点S,且其中S1~3(A城)、S4(B城)、S5(C城)、S6(D城)、S7~8(E城)、S9~10(F城)分别位于不同城市的网络单元内。单位数据在同一网络单元局域网中传输的时延及其影响都很小,且设本地访问的通信代价系数为0.1。据此模拟出实验环境I的各项统计信息(取相对值)如图3所示。 实验过程中,GA2法遗传算法的各项参数取值分别为:群体大小np=11;终止进化代数ng=50;群体初始化时预选个体数np0=50;交叉概率pc=0.9;大变异操作时,通常变异概率pm=0.05,大变异概率pmax=0.4,密集因子t∈[0.8,0.9],且随进化代数gen增加而逐渐减小,其取值如式(6)所示: (6) 图3 实验环境I中统信息 除实验环境I外,本文还模拟了站点数量分别为15和20的两个实验环境II和III。限于篇幅,其统计信息及相关参数不再列出。 在3种实验环境I、II、III下,分别运用非冗余分配最佳适宜法(简称“最佳法”),冗余分配添加副本法(简称“添加法”),启发式试消副本法(简称“试消法”),基于数据片段访问特性的分配策略(简称“特性法”)、GA1法及GA2法在Matlab工具上进行求解运算。其中GA1法、GA2法的运算结果具有随机性,此处取若干次运算的平均值,且相同环境下GA1法与GA2法种群大小及遗传终止代数取值相等。运算结果,即所得最终分配方案对应的通信总代价(数量级为105,越小越好)如表1所示。 表1 3种实验环境下不同分配策略的运算结果 3.2 实验结果分析及GA2法优越性的总结 3.1节中3种实验环境下的最佳分配方案都有一定的冗余度,采用非冗余分配最佳适宜法得到的方案自然不够理想;使用冗余分配添加副本法、试消副本法及基于片段访问特性的分配策略时,所得分配方案相对较好,但鉴于搜索广度有限,多数情况下仍存在可进一步优化的空间;由GA1法得到分配方案的质量最差,在实验环境II、III下甚至不如非冗余分配最佳适宜法;而GA2法在时耗不超过GA1法的前提下,所求得的分配方案对应的通信总代价最低。因此,相比其他策略,GA2法拥有更加优越的特性。 与同样基于遗传算法的GA1法相比,GA2法的优越性主要体现在以下几个方面:① 育种获得高质量的初始种群,使得搜索过程拥有较好的起点;② 顺序选择与最优保存相结合的选择机制在保证算法收敛性的同时,也促使选择操作更加稳定、有效;③ 大变异操作根据当前种群特征,及时补充种群多样性,提高了算法全局搜索能力。 在大型复杂工作场景的信息化建设中,本文基于改进遗传算法的数据分配策略能够为业务数据的分布式存储提供理论上的参考与支持。且相比于其他策略,以该策略为指导来解决数据分配问题更有利于系统整体访问效率的提高。但该策略只是一种静态的分配策略,仍有需要完善的地方,比如构建数学模型时为降低问题复杂度而忽略了一些次要影响因素,算法中部分参数的取值仍有待优化等等。这些问题将在后续研究中做进一步分析。 [1] 李琳琳,王庆超,姚 超,等.云存储中的数据冗余策略研究[J].无线电工程,2013,43(9): 1-3,32. [2] 齐 磊.大数据分析场景下分布式数据库技术的应用[J].移动通信,2015,39(12):58-62. [3] 岳立营.浅谈分布式数据库的数据存储[J].科技创新导报,2011(6):112. [4] 南菊松.分布式数据库系统中数据分配算法的研究[D].武汉:华中科技大学,2013. [5] Tamer O M,Patriek V.Principles of Distributed Database Systems(Second Edition)[M].北京:清华大学出版社,2002. [6] Huang Y F,Chen J H.Fragment Allocation in Distributed Database Design[J].Journal of Information Science & Engineering,2001,17(3):491-506. [7] 杨 艺.分布式数据库中数据分配方法的研究[D].重庆:重庆大学,2004. [8] 杨 洲.分布式数据库中数据分配策略的研究[D].哈尔滨:哈尔滨工程大学,2007. [9] 李 想.分布式数据库系统数据分配策略的研究[D].大连:大连理工大学,2009. [10] 王三虎.基于遗传算法的分布式数据库数据分配研究[J].西安石油大学学报,2012,27(2):102-105. [11] 张德生.基于遗传算法的大型数据库的数据分配策略算法[J].科技通报,2015,31(1):162-165. [12] 彭 璐,何加铭.基于遗传算法的多约束QoS单播路由算法[J].移动通信,2015,39(6):76-81. [13] 王小平,曹立明.遗传算法—理论、应用与软件实现[M].西安:西安交通大学出版社,2002. [14] 谈 敏,蔡 钧.基于改进遗传算法的双频滤波器自动设计[J].无线电工程,2012,42(10):48-50. [15] 雷英杰,张善文.遗传算法工具箱及应用[M].西安:西安电子科技大学出版社,2014. [16] 龚 纯,王正林.精通MATLAB最优化计算(第2版)[M].北京:电子工业出版社,2012. Research of Data Allocation Strategy in DDB Based on Genetic Algorithm YUAN Xu,SUN Ji-min (The 54th Research Institute of CETC,Shijiazhuang Hebei 050081,China) In order to improve further the accessing efficiency of DDBS,this paper analyzes the data allocation problem and builds a corresponding mathematical model in consideration of practical application.Based on the existing research of solving this problem with genetic algorithm,new measures are adopted to improve the genetic algorithm,for examples,an excellent original population is created by selective breeding in the initialization phase,the individuals are chosen by a rule which combines order selection and elitist selection during the evolutionary process,the big mutation is utilized to broaden the searching extent of the algorithm,and so on.Then a new data allocation strategy is put forward.The simulation results show that this strategy can be used to get a better data allocation scheme compared with other methods. data allocation;genetic algorithm;distributed database;data storage 10.3969/j.issn.1003-3114.2017.01.10 袁 旭,孙纪敏.基于遗传算法的分布式数据库数据分配策略研究[J].无线电通信技术,2017,43(1):39-43. 2016-09-19 国家部委基金资助项目 袁 旭(1991—),男,硕士研究生,主要研究方向:分布式数据库。孙纪敏(1963—),女,研究员,主要研究方向:软件工程、计算机应用。 TP311 A 1003-3114(2017)01-39-53 仿真实验及结果分析


4 结束语

