多周期信号的小波包方差分析方法

马亚男，戴尔晗，陈 诚

(南京邮电大学 自动化学院，江苏 南京 210023)

多周期信号的小波包方差分析方法

马亚男，戴尔晗，陈 诚

(南京邮电大学 自动化学院，江苏 南京 210023)

在多周期结构分析中，最大重叠离散小波变换得到的信号周期具有明显的局限性。在对比小波方差分析中，提出了用最大重叠离散小波包方差法分析不同尺度小波方差图、功率谱，从而得到信号周期估计的最大值。实验结果表明，对信号或时间序列周期结构的分析是一种有效的方法，该方法可以准确估计多周期信号的小波包方差。

功率谱；多周期；小波方差；小波包方差

0 引言

高分辨谱估计是信号处理中的一个热点问题。一个信号的周期性结构，在光谱分析中有两种方法：FFT谱估计方法和现代谱估计方法。传统的傅里叶变换方法只适用于平稳信号分析，其分辨率是固定的。当数据长度较短时，分辨率较低，且不能同时对高频信号进行分析。所以，在应用程序中有很大的局限性[1]。近年来，一些研究人员提出了基于小波变换的现代谱估计方法，对频率分辨率和估计精度有了较大的提高[2-3]。这些方法已逐渐被应用于金融、气象、水印、海洋、机械、医疗和电子信号处理领域[4-6]。信号周期旋转后，功率谱的周期结构发生变化[7-8]，因此，离散小波变换不能直接用于信号的周期结构分析。

本文将基于MODWT小波方差有效地分析估计信号的频谱，从而分析信号的周期结构。DWT和MODWT有良好的低频频率分辨率,但有较低的高频频率分辨率；自然极大重叠离散小波包变换(MODWPT)被认为具有更好的频率分辨率，高频率可取代MODWT。由于小波系数的突出优势和MODWT的缩放系数满足平移不变性、各分解层保持相同的分辨率和无相位失真，MODWPT非常适合于非平稳信号处理[9]。实验结果表明，使用基于MODWPT的方法来仿真信号的周期性结构具有良好的效果。

1 小波方差法

1.1 小波方差的定义

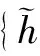
(1)

{Xt}基于尺度τj=2j-1的小波方差定义如下：

v2(τj)=var{Wj,t}

(2)

1.2 小波方差估计

(3)

(4)

其中Mj=N-Lj+1，且Lj是第j阶等效小波或缩放滤波器的宽度。

2 小波包方差法

(5)

(6)

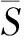
(7)

3 基于小波包方差周期结构分析

下面有5个正弦周期模拟信号：

xt=sin(2×100πt)+sin(2×175πt)+sin(2×200πt)+sin(2×300πt)+sin(2×320πt)

(8)

频率分别为f1=100 Hz，f2=175 Hz，f3=200 Hz，f4=300 Hz，f5=320 Hz。周期分别为T1=0.01 s，T2=0.005 7 s，T3=0.005 s，T4=0.003 3 s，T5=0.003 1 s。采样周期为0.001 s，采样点的数量是1 000。因此，该信号可以看作是一个离散时间序列。

式(8)中,xt是在MODWPT基础上在τ8=28Δt=0.256 s的尺度下由db4小波分解了6层和8层进行小波方差的估计。计算出频率对应于不同尺度的小波包的频率区间。基于MODWPT的小波包方差图如图1(a)和(b)所示。图1(a)表示尺度为0.064s的小波方差。图1(b)表示尺度为0.256s的小波方差。

从图1可以看到，小波方差图可以分为5大峰，其频率大致为100Hz、175Hz、200Hz、300Hz和320Hz。下一个峰值发生在最大峰值处。从图1可以得出结论：分解层数增加，泄漏更严重。

图1 小波包方差图

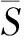
图2 小波包方差估计

有一个高频信号如下：

xt=sin(2×20 000πt)+sin(2×20 500πt)

(9)

根据MODWPT采样周期是0.000 01s和采样点的数量为10 000，信号被分解为10个等级，小波包方差如图3所示，实际尺度为τj=210Δt=0.010 24 s。对应的两大峰值的频率分别为f1≈20 000 Hz,f2≈20 500 Hz。因此，小波包方差的方法可以有效地识别高频信号周期结构。

图3 高频信号的小波包方差图

当尺度较大时，观测范围内的时间轴也较大。例如，一个低频信号如下：

xt=sin(2×0.4πt)+sin(2×0.5πt)+sin(2×0.6πt)

(10)

采样周期为0.5s，采样点的数量是2 000。在MODWPT基础上信号可以分解为5层，其中实际尺度τj=16 s，小波包方差图如图4所示。三大峰对应的频率分别为f1≈0.4 Hz,f2≈0.5 Hz,f3≈0.6 Hz。它表明，小波包方差的方法可以有效地识别低频信号周期结构。

图4 低频信号的小波包方差图

基于MODWPT分析信号的小波包的变异时，理论上可以在低频或高频获得高分辨率。但是由于小波变换的特殊性，当尺度因子减小时，小波包的时域波形变小，这相当于频率域的波形变宽，意味着带通滤波器更宽。如果减少了步长因子，小波包方差图不理想，原因是衰减很慢，并伴随着泄漏。

4 结论

使用基于MODWT或MODWPT时间信号的多尺度分

析可以避免初始点和信号长度的影响，而且还可以以不同的频率有效地分解方差的序列。基于MODWT方法仅在低频分析小波方差时有效，所以准确性估计的程度是有限的。信号的低频和高频域可以分别基于MODWPT被分解，因此可以得到比MODWT更高的分辨率。这表明，小波包方差法能更准确地估计多周期结构。此外，也可以在噪声信号的多周期结构分析中使用基于小波包方差的方法。仿真结果表明，通过MODWPT分析小波包方差和功率谱，信号周期的频率可以有效地估计。它提供了一种信号或序列的周期性结构分析的有效方法。

[1] HERLEY C, VETTERLI M. Wavelets and recursivefilter banks[J]. IEEE Transactions on Signal Processing, 2013,41(8): 2536-2556 .

[2] 李芬华，潘立冬，常铁原，等.精密频谱分析系统的设计与实现[J]. 电力自动化设备,2002,22(12):40-43.

[3] 张瑛，牟龙华，刘军.电力系统频率测量及跟踪[J]. 电力系统及其自动化学报，2003,15(3) :35-36.

[4] AGHAZADEH R,LESANI H,SANAYE-PASAND M,et al.New technique for frequency and amplitude estimation of power system signals[J]. IET Proceedings of Gener. Transm. Distrib.,2005,152(3) :435-440.

[5] NEWLAND D E. Ridge and phase indetification in the frequency analysis of transient signals by harmonIc wavelets[J] .Journal of Vibration and Acoustics, 1999,121(2):149-155 .

[6] SHERLOCK B G,KAKAD Y P. Windowed discrete cosine and sine transforms for shifting data[J].Signal Processing,2001,81(7): 1465-1478 .

[7] 胡茑庆,温熙森，陈敏.随机共振原理在强噪声背景信号检测中的应用[J].国防科技大学学报,2001,23(4): 40-44 .

[8] Wang Guanyu. The application of chaoticoscillator stoweak signal detection[J] . IEEE Transactions on Industrial Electronics,2001,46(2): 440-444 .

[9] 李一兵，岳欣，杨莘元．多重自相关函数在微弱正弦信号检测中的应用[J].哈尔滨工程大学学报，2004，25(4):525-528.

Wavelet packet variance analysis methods for multi-period signal

Ma Yanan,Dai Erhan,Chen Cheng

(School of Automation, Nanjing University of Posts and Telecommunications,Nanjing 210023, China)

In the multi-period structure analysis, the period of signal obtained by the maximal overlap discrete wavelet variance has significant limitations. In this paper, in contrast to the wavelet variance analysis, we present a method of maximal overlap discrete wavelet packet variance to analyze the variance diagram or power spectrum at different scales, and then obtain the period of signal by estimating the maximum value. Experimental results show that the method of wavelet packet variance can estimate the multi-period structure of the signal accurately. It is an effective method for signal or time series periodic structure analysis.

power spectrum; multi-period; wavelet variance; wavelet packet variance

TP216+.1

A

10.19358/j.issn.1674- 7720.2017.03.024

马亚男，戴尔晗，陈诚.多周期信号的小波包方差分析方法[J].微型机与应用，2017,36(3)：82-84.

2016-08-09)

马亚男(1994-)，女，硕士研究生，主要研究方向：信号周期检测。

戴尔晗(1973-)，男，硕士，副教授，主要研究方向：计算机，测控系统，电力电子。

陈诚(1991-)，男，硕士研究生，主要研究方向：信号周期检测。