载体高精度惯导辅助动中通传递算法

王梓函，姚敏立，闫志翔，何 芳，胡朝军

（火箭军工程大学，陕西 西安 710025）

载体高精度惯导辅助动中通传递算法

王梓函，姚敏立，闫志翔，何 芳，胡朝军

（火箭军工程大学，陕西 西安 710025）

为降低载体上动中通的测控成本，提高其测控精度。本文提出一种利用大型载体上的高精度惯导辅助动中通进行天线校正的传递测控算法。针对大型载体的动态形变导致传递测控产生较大偏差的问题，采用一种利用卡尔曼滤波算法精确估计载体的动态形变以补偿传递测控算法中的动态误差的方法。仿真分析了迭代算法与卡尔曼滤波算法对船体动态形变估计的偏差，并对比分析传递对准姿态与从惯导姿态对参考值的估计误差。对仿真结果进行分析：卡尔曼滤波算法与迭代算法相比对载体动态形变估计更为准确。互补滤波的传递测控算法与从惯导直接测量滤波相比更接近参考值。仿真结果说明：通过传递测控算法利用精确惯导辅助低成本动中通进行精确测控的方法有效可行。

高精度惯导；动中通；动态形变；卡尔曼滤波；传递算法

0 引 言

现有的动中通大致可以分为两类：一类是采用低成本、低精度的机械陀螺作为测量单元的民用动中通。该类动中通采用低成本的测量单元，大多情况下应用于路况较好的情况，而在复杂的地况条件下，天线的指向精度明显下降，应用环境受限[1-2]。另一类是采用高精度的惯性器件或组合作为测量单元的军用动中通系统。该类系统可以精确测量运动中载体的姿态信息，通过有效的姿态估计算法即可获得准确的天线修正角，从而对天线波束进行实时调控[3]。

国外研制高精度惯导动中通的成功案例有很多，例如美国的ERA公司研发的Spitfire低轮廓Ku波段动中通[4]，其采用惯性导航系统能够提供可靠的姿态数据，对动态性较强的飞机、车辆以及复杂战场环境下的车辆等应用载体都有着较高的通信能力。

纵观国内外高级移动载体（如坦克、航空飞机和大型舰艇等），均使用成本更高更稳定的高精度惯导动中通，但恰恰由于其成本较高，制约了高精度惯导动中通的推广和应用。

本文提出利用高级移动大型载体主惯导来辅助低成本动中通对天线姿态的精确控制的想法。

采用惯性测量匹配法能在载体上的不同位置获得相对于主惯导的相对指向从而可以加以利用主惯导的精确测控信息。假设船体的动态形变很小，认为陀螺输出是线性的，根据线性最优卡尔曼滤波能够有效估计载体的动态形变。此外，通过迭代算法、卡尔曼滤波算法等，能够有效估计两个惯导间的动态形变，能够近似估计载体上不同位置之间的动态形变。

1 数学模型

1.1 坐标变换与角速率匹配

为了实现利用外来惯导辅助动中通测控系统完成天线波束的精确调控，首要解决的问题是精确估计载体的动态形变，以便实现传递测控[5]。

以大型轮船为例，由于轮船工业制造的承受力产生弯曲形变以及安装误差（静态误差）等原因，往往使位于较远位置的从惯导 （slave inertial navigation system，SINS）坐标系与处于中心位置的主惯导（master inertial navigation system，MINS）坐标系的指向不统一。

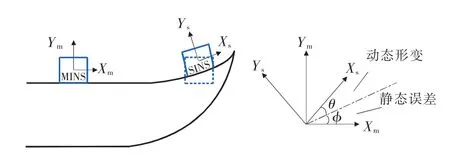
图1 船体主从惯导结构示意图与形变关系图

为了将船体上各个位置的姿态信息统一到同一坐标系中，研究船体的动态形变误差就很有必要性。

一般情况下，处于不同位置上的惯导测得的船体形变一般包含静态误差和动态形变，如图1所示。而二阶马尔科夫的各种参数能够有效地仿真载体形变的真实情况，从而有效模拟船体结构的动态形变。为了实现载体主惯导辅助测控算法的实现，本文首先介绍载体上惯导间的坐标变化情况，以及信息在载体上的共享方法[6]。

为实现在主惯导坐标系 oxmymzm和从惯导坐标系 oxsyszs之间的变换，设定 φz表示夹板平面的弯曲角；φx表示船体纵向弯曲角；φy表示绕纵向轴的扭力角，从 oxmymzm到 oxsyszs的传递过程[7]可以表示为

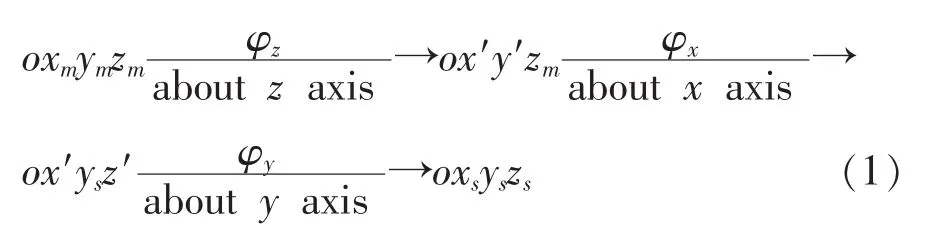
坐标系oxmymzm到坐标系oxsyszs的转化用旋转矩阵表示如下：

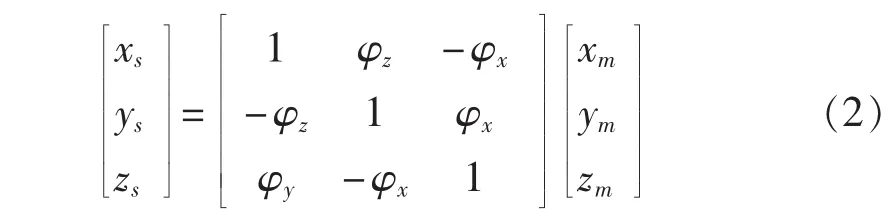
则坐标系相互转换的旋转矩阵为

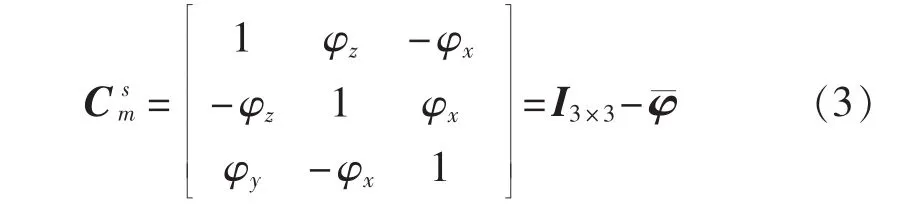
式中：I3×3——三阶的单位矩阵；

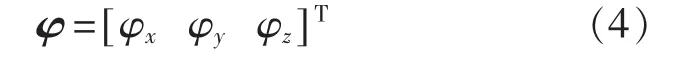
主惯导测得船舶的角速率矢量在坐标系oxmymzm为；从惯导测得船舶的角速率矢量在坐标系oxsyszs中为则两者的关系为

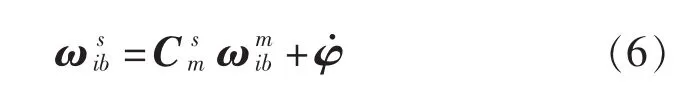
不同的惯导所测得船舶的姿态角的误差角可以表示为

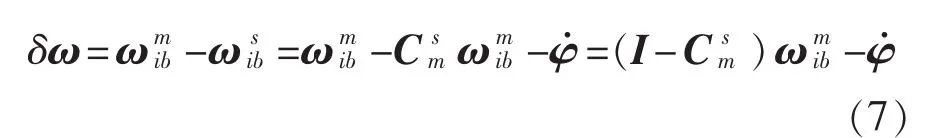
式（7）写成矩阵形式为

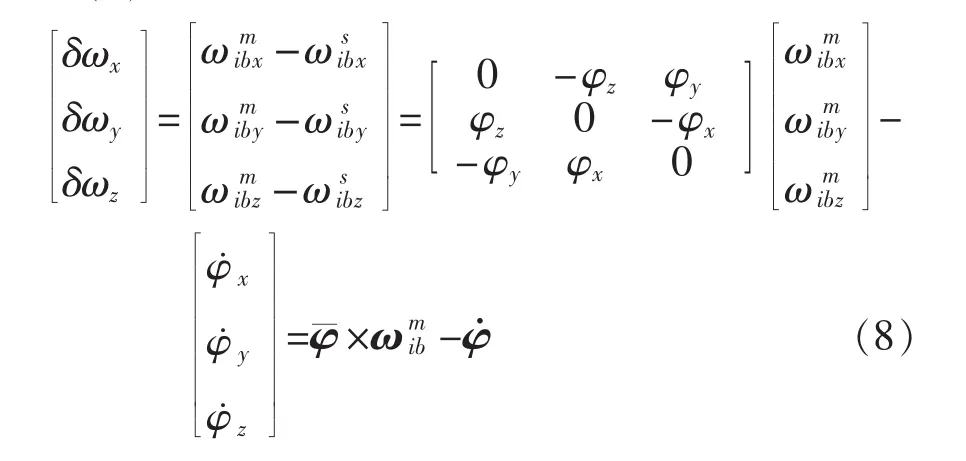
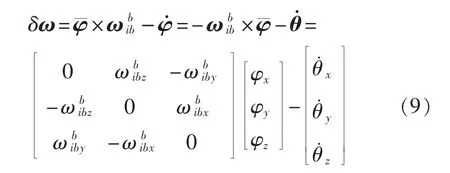
1.2 模拟动态形变

载体的动态形变类似于一个随机过程，可以用一个相关函数近似表示为

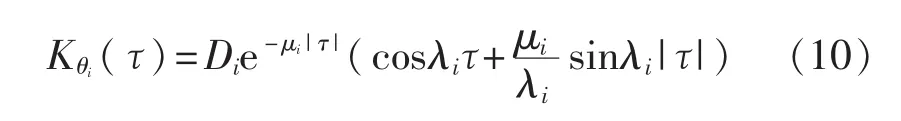
式中：μi——不规则系数；

λi——动态形变的噪声频率；

Di——动态形变系数。

式（10）通过变形可以得到：

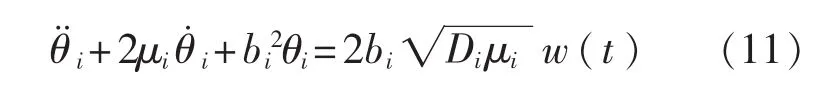
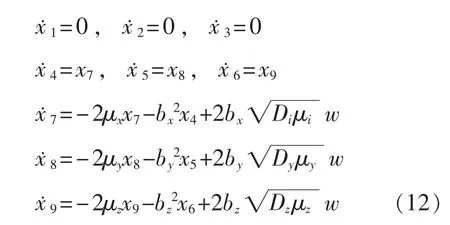
式中：x1，x2，x3——静态误差；

x4，x5，x6——动态误差；

x7，x8，x9——三轴的动态误差角速率[8]。

2 卡尔曼滤波算法

2.1 状态方程

由于主惯导是高精度惯导，所以其陀螺漂移近似为0。从惯导是低精度的，其陀螺漂移是随机的。随机过程的相关函数[9]可以表示为

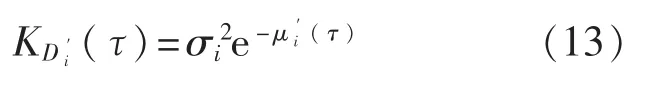
其变形等式可以表示为

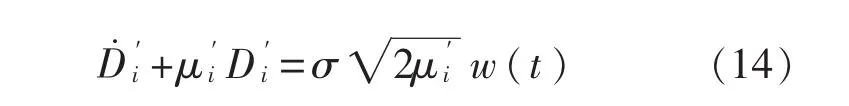
其中w（t）是均值为0、方差为1的高斯白噪声。状态等式中从惯导误差的随机漂移可以表示为

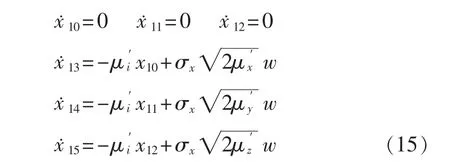
则卡尔曼滤波的状态方程表示为

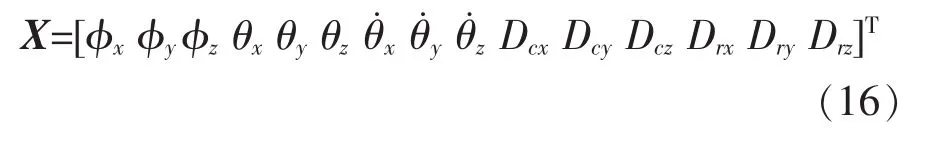
其矩阵形式为

其中状态转移矩阵为

2.2 量测方程

量测值包含主从惯导输出的陀螺数据值

量测方程表达式为

式中：z=[δωxδωyδωz]T；

ν——量测噪声；

H——观测矩阵，

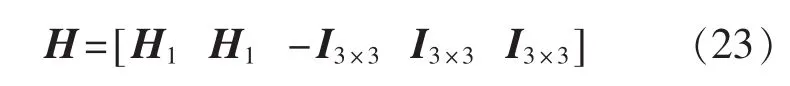
其中

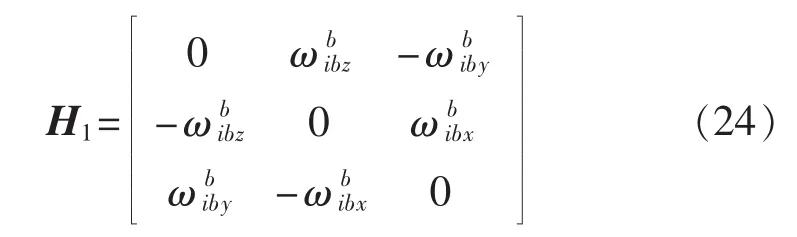
3 传递测控算法

假设载体的形变量为φ=[φxφyφz]T，静态形变为θ=[θxθyθz]T，则载体形变为

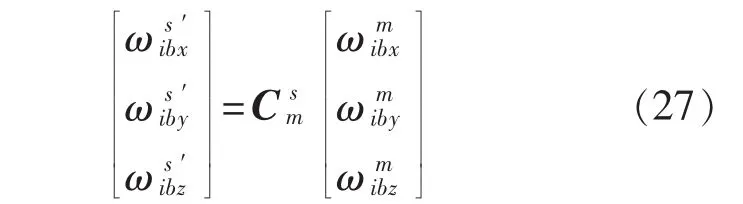
式中ψ=Φz，θ=Φy，φ=Φx。通过主从惯导所测得到的角速率δω′为

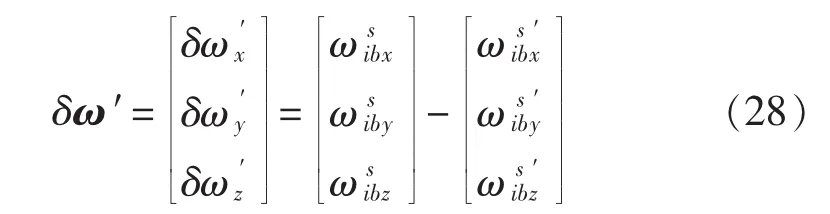
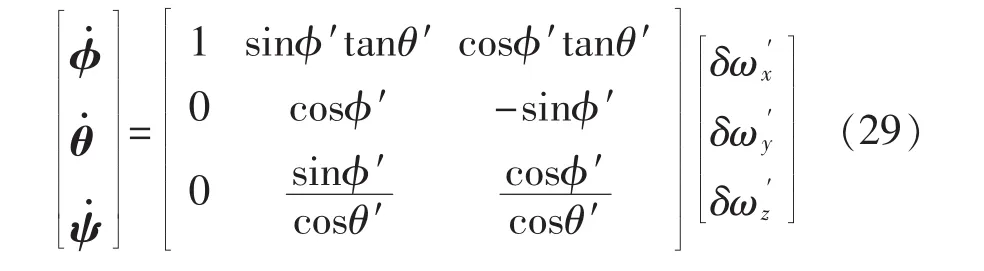
将得到的修正量通过转化方程传送到三轴陀螺，得到的陀螺修正数据为

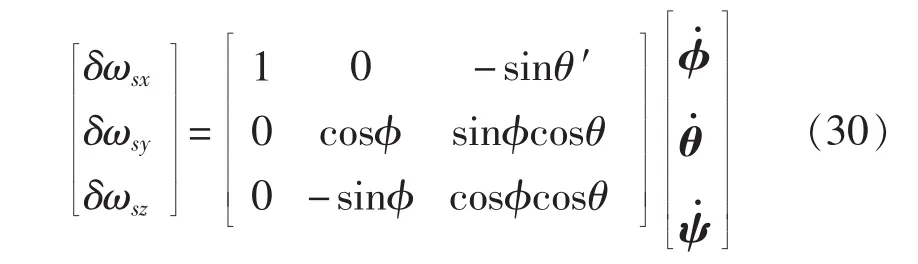
将陀螺修正数据传送到动中通的伺服控制系统，完成载体主惯导的传递对准[11-12]。

4 仿真结果与分析

通过二阶马尔科夫过程模拟载体的动态形变，利用迭代算法和卡尔曼滤波算法对载体形变进行仿真实验。仿真条件是高精度惯导（主惯导）的常值漂移为0.1°/h，随机漂移为0.01°/h，采样间隔为0.01s，载体的初始角度P=0°，R=0°，H=90°；将载体在行驶过程中的三轴变化定义成一种正弦变化：

载体的安装误差Φx=40″，Φy=20″，Φz=10″，动态形变角（D-phix，D-phiy，D-phiz）可以通过二阶马尔科夫过程来模拟，其中设（μi=0.02，λi=0.1）。根据仿真数据进行模拟，图2表示模拟的主惯导三轴角速率[ωxωyωz]；仿真依据船舶在行驶过程中各个参量的变化情况而定，时间为10min。图3是根据二阶马尔科夫过程模拟仿真的载体三轴动态角。

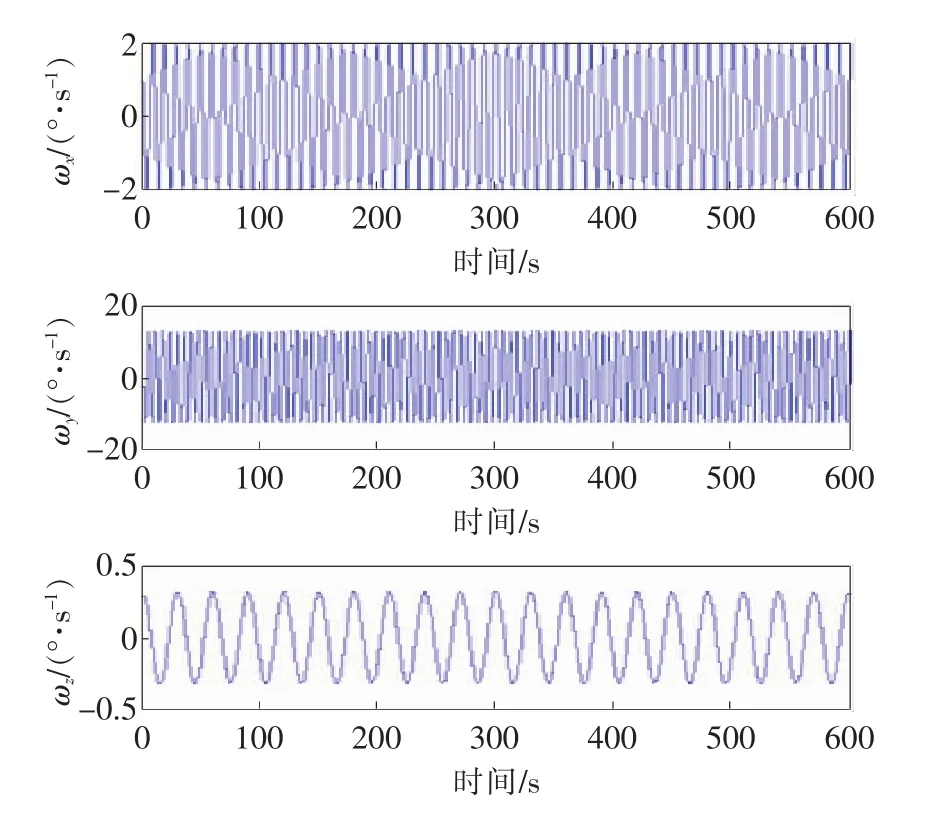
图2 模拟主惯导角速率图

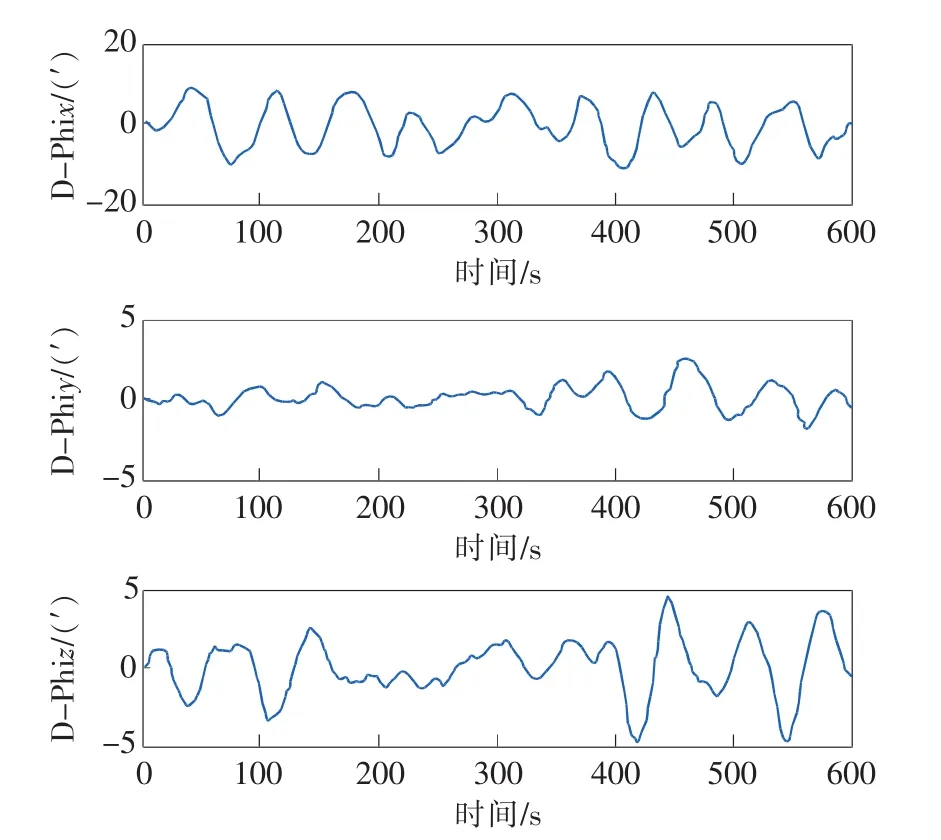
图3 模拟动态形变角

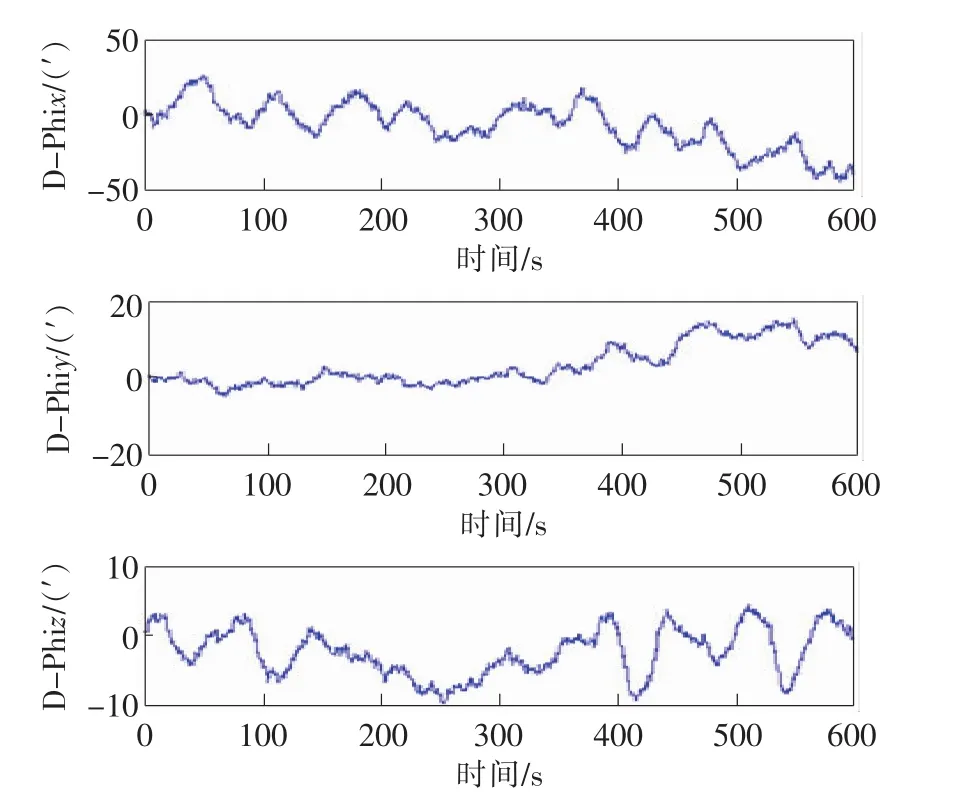
图4 迭代载体动态形变角图

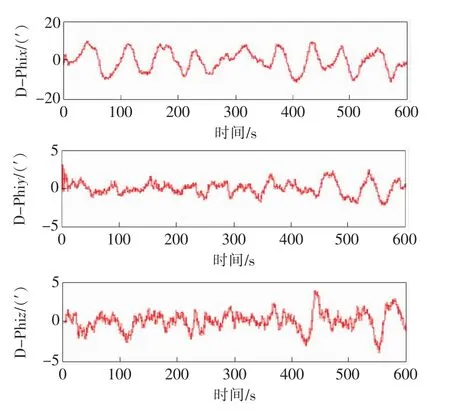
图5 卡尔曼估计动态形变角

用传统模型和卡尔曼滤波法对载体的动态形变进行估计，从图4和图5中可以得出，两种方法都能很好地反映载体的动态形变特性。从迭代形变动态角的纵坐标变化量可以发现，迭代过程中的误差会造成整体误差随时间的增加而不断累积，导致误差较大；用卡尔曼滤波算法进行估计产生的误差较小。为了验证算法的有效性，模拟仿真了在波动的海平面上进行行驶实验。由于波浪的不断涌动导致大型舰艇在行驶过程中会出现较大的载体形变，载体形变模拟仿真结果如图6所示。

从图中可以看出载体的动态形变角基本保持在一个固定值，然后上下波动。这与舰艇行驶在波浪海平面有关，形变角度也是根据舰艇受不同外力导致的形变而设定。其中φx受波浪起伏影响较大；φy受舰艇左右摇摆影响较大；φz受外力导致船身扭动的影响。

惯导的随机漂移仿真结果如图7所示。

图6 模拟载体动态形变角

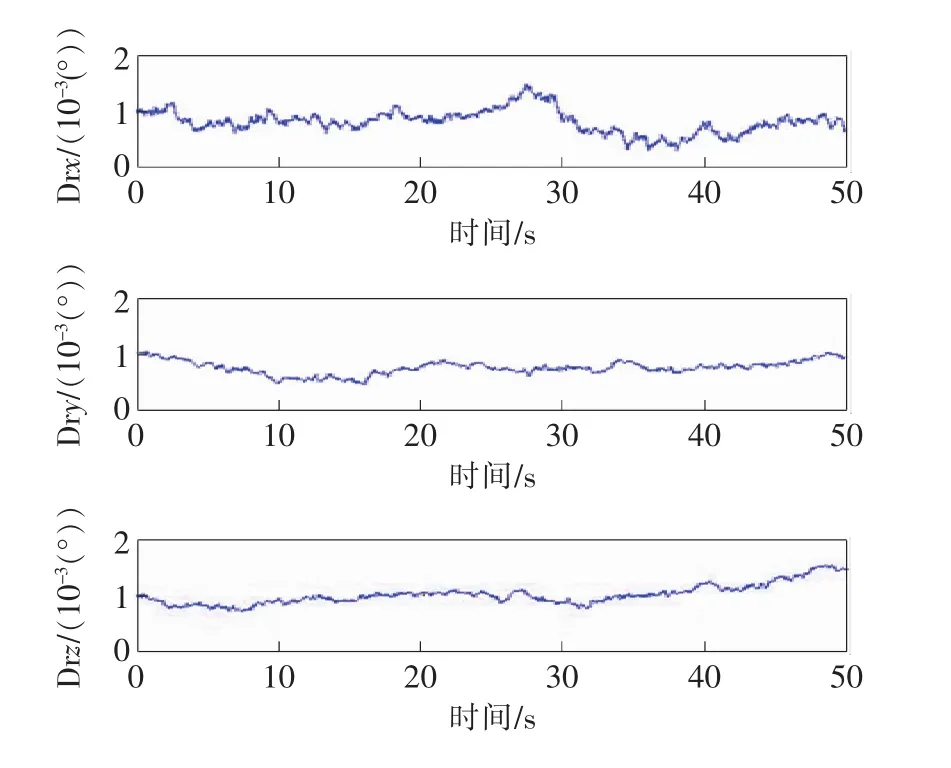
图7 从惯导陀螺漂移误差

给出一组参考值，模拟高精度惯导动中通的测量值，并仿真模拟对主惯导测量值进行传递算法修正到低成本动中通的修正值，以及模拟仿真对低成本动中通的测量值进行补偿去漂移误差算法的修正值。通过对两种方法仿真得出的修正值进行对比，可以非常直观地看出传递算法与参考值（真实值）更为接近。从惯导测得角速率和传递修正角速率对比见图8，传递对准姿态和从惯导姿态估计对比见图9。

从图9中可以看出由于测控精度较低，从惯导所量测的数据经过误差消除后，所得到的信息不能完全准确反映天线波束的变化情况，有部分信息其中包含载体形变角速率；而互补滤波传递测控算法能够较好地实现天线波束的变化角速率的测量，为天线波束的测控提供了可靠的观测值。

观察图8、图9还可以发现，当载体动态形变较大时，从惯导的陀螺数据能明显反映出这种动态误差贯穿于运动的始终，而传递测控算法实现天线的姿态校正，图中显示了从惯导直接测量所得的姿态估计结果和传递对准修正后的结果。可以明显看出，利用高精度惯导对大型载体上移动卫星通信系统进行传递对准，与从惯导姿态估计相比较，能更精确地满足天线姿态的估计精度，对准效果更为良好。

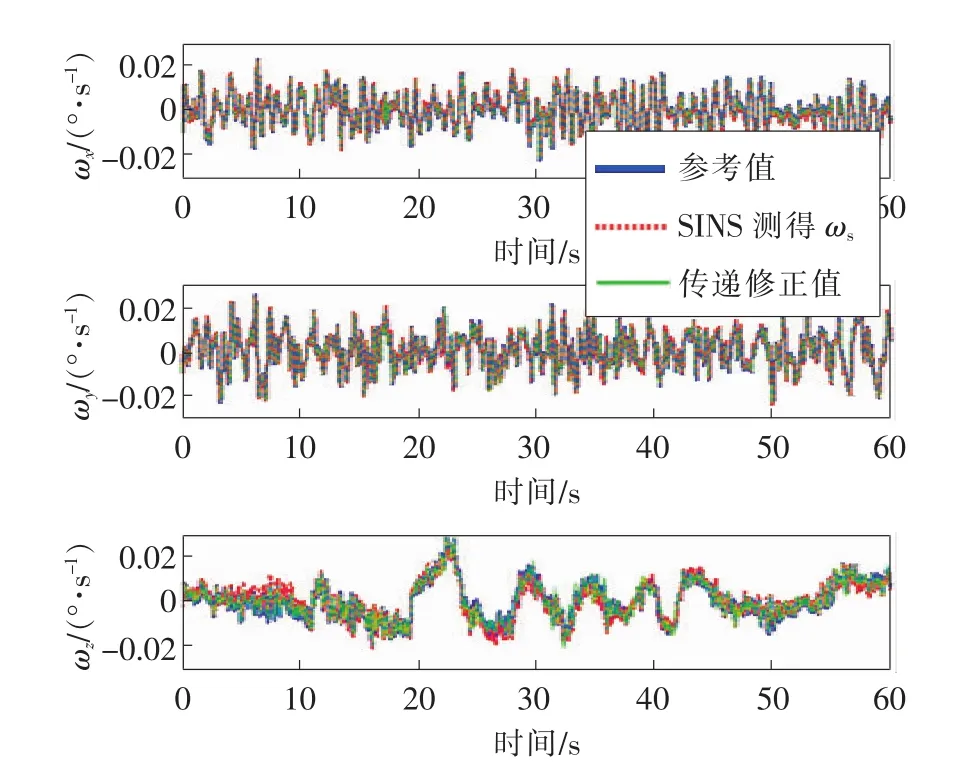
图8 从惯导测得角速率和传递修正角速率对比图

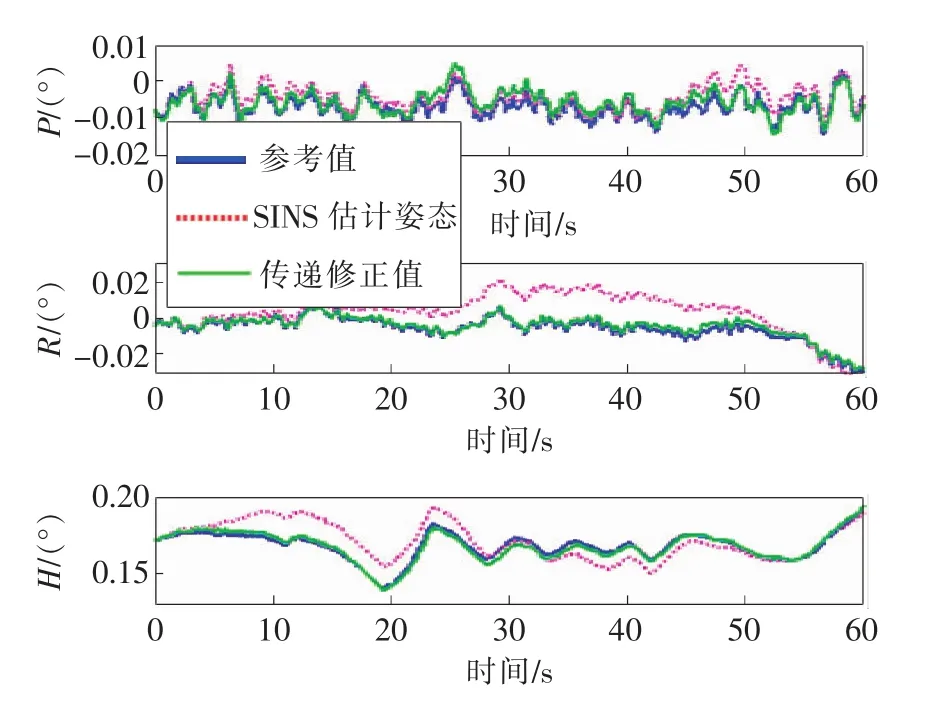
图9 传递对准姿态和从惯导姿态估计对比图

5 结束语

本文在产生有形变、存在动态误差的大型载体上，先通过卡尔曼滤波算法对船体的形变进行估计，再通过互补滤波传递测控算法，利用高精度惯导对低成本动中通进行姿态纠正。原有的迭代算法随着时间的增加，从惯导的测量误差随之增大，从惯导的累积漂移误差将不断影响着天线姿态的估计结果，如果长时间没有主惯导的修正，将会丢失卫星导致信号中断。仿真结果表明：卡尔曼滤波算法与迭代算法相比对载体动态形变估计更为准确，互补滤波的传递测控算法与从惯导直接测量滤波相比更接近参考值。本文所提出的利用载体高精度惯导辅助动中通的传递测控算法有效可行，降低了动中通的应用成本，提高了大型载体上的移动通信能力，可促进动中通的推广和发展。

[1]HILKERT J M.Inerially stabilized platform technology concepts and principles[J].IEEE Control Systems Magazine，2008，28（1）：26-46.

[2]刘丰．Ku波段动中通卫星天线的发展现状和应用情况[C]∥中国卫星应用大会-2007论文集，2007：33-46．

[3]ALBERTS D S，GARSTKA J J.Network Centric Warfare[M]．America CCRP，2004：33-45.

[4]闫志翔，姚敏立，赵建伟，等.移动卫星通信系统强跟踪姿态估计算法[J].电光与控制，2016（2）：324-327，332.

[5]ZHENG R C，YANG G L，CHEN C Y.Uniform attitude reference measurement system of the whole ship based on data fusion[C]∥Proceedings of 2010 International Symposium on Inertial Technology and Navigation，2010.

[6]WANG X Q，CHEN X Y.Inertial measurement method ofship dynamic deformation[J].Journal of Chinese Inertial Technology，2006，14（2）：24-28.

[7]SALMAN M J.Performance improvement of angular rate matching shipboard transfer alignment[C]∥Proceedings of2009 9th InternationalConference on Electronic Measurement&Instruments，2009.

[8]吕遐东，刘佳铭，姚腾钢.船舶动态变形特性分析与测量方法研究[J].华中科技大学学报，2014（S1）：117.

[9]姚敏立，伍宗伟，张峰干，等.动中通卫星通信系统级联卡尔曼滤波载体姿态估计方法[D].西安：第二炮兵工程大学，2015.

[10]丁国强.惯性导航系统传递对准技术关键问题研究[D].哈尔滨：哈尔滨工程大学，2010.

[11]高伟，张亚，孙骞，等.传递对准中杆臂效应的误差分析与补偿[J].仪器仪表学报，2013，34（3）：559-564.

[12]陈雨，赵剡，李群生，等.快速传递对准中主惯导信息滞后补偿方法[J].中国惯性技术学报，2013，21（5）：576-580.

（编辑：李刚）

Transfer algorithm based on high-precision inertial navigation system assisting SOTM on carrier

WANG Zihan，YAO Minli，YAN Zhixiang，HE Fang，HU Chaojun
（Rocket Force University of Engineering，Xi’an 710025，China）

To reduce cost of the SOTM (satcom on the move)measurement and control，improve measurement and control precision，the paper proposes a transfer algorithm that applies the highprecision inertial navigation system on large carrier to assist SOTM for antenna calibration.For the problem that large transfer measurement and control error will be caused by dynamic deformation of large carrier，a method that uses Kalman filter algorithm to accurately estimate the dynamic deformation of carrier to compensate the dynamic error in transfer algorithm is applied.Simulative analysis is carried out for estimates of dynamic deformation of ship with iterative algorithm and Kalman filter algorithm and contrastive analysis is carried out for estimates of reference value with transfer alignment attitude and inertial navigation attitude.Through analysis on simulation results，it can be found that Kalman filter algorithm has more accurate estimates of dynamic deformation of carrier than iterative algorithm and the transfer algorithm based on complementary filter has value more approximate to reference value than inertial navigation based on direct filter measurement. Therefore，using precise inertialnavigation system to assistlow-costSOTM foraccurate measurement and control with the transfer algorithm is feasible and effective.

high-precision inertial navigation；SOTM；dynamic deformation；Kalman filters；transfer algorithm

A

：1674-5124（2017）01-0106-06

10.11857/j.issn.1674-5124.2017.01.022

2016-05-22；

：2016-07-13

国家自然科学基金（61179005，61501469）

王梓函（1992-），男，北京市人，硕士研究生，专业方向为移动卫星通信。