X80管线钢拉伸载荷作用下磁记忆效应

贾 东，孙 乐，陈勇梅，牛 伟

（中国工程物理研究院总体工程研究所，四川 绵阳 621900）

X80管线钢拉伸载荷作用下磁记忆效应

贾 东，孙 乐，陈勇梅，牛 伟

（中国工程物理研究院总体工程研究所，四川 绵阳 621900）

为研究X80管线钢的金属磁记忆效应，通过不同载荷水平的板材拉伸加-卸载以及离线磁场测量，结合多项式拟合与矢量分析，得到试件表面磁场长度方向分量极值、法向分量梯度值以及合成矢量的变化规律，并根据应力等效磁化模型对其进行解释。研究结果表明：在加载环境磁场和拉伸载荷的耦合作用下，磁场长度方向分量极值和法向分量梯度值均呈现出单调递增的变化规律，而磁场矢量会发生反转。当载荷在20kN以内时，长度方向分量极值和法向分量梯度值均随载荷幅值增加而缓慢增加，磁场矢量大小及其与长度方向的夹角随载荷增加而缓慢减小；而当载荷大于20kN时，长度方向分量极值、法向分量梯度值以及磁场矢量大小均呈线性增加趋势，磁场矢量方向发生反向并逐渐趋于恒定。

金属磁记忆效应；应力磁化；磁场矢量；X80管线钢；拉伸载荷

0 引 言

俄罗斯Doubov教授[1]提出的金属磁记忆检测技术是近年来逐渐兴起的一种重要的无损检测方法，通过铁磁构件磁化后保留下来的磁信号检测来评价其应力集中和缺陷状态。磁记忆检测方法的理论基础是铁磁材料的磁机械效应，不少专家学者也开展了相关研究。在国外，Jiles等[2-3]针对铁磁材料的应力磁化效应开展了大量深入的研究，并给出了相应的应力磁化模型；Wilson等[4]通过拉伸加载后的剩余磁场对试件的应力进行测量；Roslpsz等[5]分析了循环加载下磁场法向及切线分量的变化特征，并给出了磁场信号与应力状态之间的对应关系。在国内，王正道等[6-7]在Jiles的力磁耦合模型基础上开展了新的理论研究，并对拉压应力在应力磁化作用上的区别进行了解释；徐滨士等[8-9]研究了金属磁记忆的产生机理，分析了铁磁构件循环拉伸载荷下的磁场分量的变化规律；徐明秀等[10]分析了金属磁记忆过程的微观机制。

作为油气管道最为常用的管线钢材，X80管线钢被广泛应用于油气输运的各类管线，其安全状态的准确检测对国家能源安全和经济有着重要意义。考虑到油气管道运营过程中主要受拉伸载荷作用，本文以X80管线钢板材试件为对象，通过不同载荷水平的加-卸载拉伸实验研究其应力磁化效应，为管线钢的磁记忆检测提供一定的理论基础。

1 实验方法

1.1 材料参数及试件设计

实验采用的材料为X80管线钢，其弹性模量约为190GPa，泊松比为0.3，屈服强度约为550MPa。为避免几何效应对试件磁场分布的影响，这里采用规则的无缺陷长方形板材试件进行单轴拉伸加载实验，试件的长度、宽度和厚度分别为500mm×50mm×5mm。

1.2 实验加载及测试方案

通过材料试验机INSTRON 5988对试件沿竖直方向进行拉伸加载，试件加载方向与南北方向垂直，表面法向与南北方向平行。考虑到延性金属塑性变形时会发生颈缩现象，导致试件出现不可逆的几何形变，所以这里根据X80管线钢的材料参数，为保证试件在弹性范围内进行加载，设定载荷值分别为0，10，20，40，60，80，100，120 kN共8种不同的实验加载条件，具体加载方式如图1所示。

图1 实验加载过程

在实验加载前，对板材试件进行退火处理，尽量消除试件中由于加工制造产生的残余应力，然后采用消磁器对沿东西方向放置的试件进行消磁处理，得到待加载的实验试件。将试件沿南北方向水平放置于地磁场环境中，在2 mm的提离高度下，采用Bartington磁通门传感器对试件中部（300mm以内）表面中心轴线由南向北每隔10mm进行一次数据采集（如图2所示），获取试件表面中心轴线在未加载情况下的磁场分量。

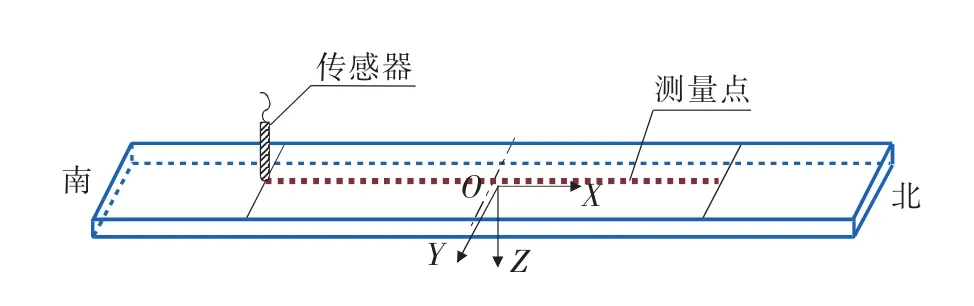
图2 试件表面磁场测量

然后通过试验机以恒定速率将试件加载到设定载荷点，并保载2min，再进行卸载并取下试件，将试件放置于地磁场环境下进行离线测量，获取试件表面中心轴线在不同拉伸载荷作用后的磁场分量。

2 实验结果

2.1 加载和测量时的环境磁场

由于试验机夹持装置存在铁磁构件，且在工作载荷作用下发生了磁化，所以试件加载环境磁场并不均匀，如图3（a）所示。而对于试件离线测量时的环境磁场，由于周围无其他磁源影响，所以其磁场基本为恒定磁场，如图3（b）所示。

2.2 试件表面磁场分布

由于试件为长方形板材构型，加载、测量时宽度方向（Y方向）的环境磁场分量趋于0且试件沿南北方向放置，拉伸载荷对试件宽度方向（Y方向）的磁场分量影响较小，所以这里主要分析试件的长度方向（X方向）及法向（Z方向）磁场分量在不同载荷水平作用后试件表面中心轴线上磁场分布，如图4所示。

由测量结果可以看出，X80管线钢在拉伸载荷作用下的磁记忆效应非常明显，随着载荷的增加，试件长度方向磁场分量整体大小和法向磁场分量的斜率都不断增大。

图3 环境磁场分布

3 分析与讨论

3.1 拉伸加载对磁场分量的影响

对于放置于外磁场环境中的铁磁试件，其周围空间磁场是由环境磁场和铁磁试件引起的附加磁场两部分组成，所以为了更好地分析拉伸加载对试件本身磁场分布的影响，利用矢量叠加原理得到去除环境磁场后的长度方向和法向磁场分量，如图5所示。

从试件测量区域磁场分量的分布形式上看，在不同拉伸载荷作用后，沿试件中心轴线的表面磁场长度方向分量均有极值特征，法向分量均呈现出三次曲线分布形式且所有曲线均过零点。所以这里分别采用二次和三次多项式函数对长度方向分量和法向分量进行拟合，并以拟合后的二次函数极值和三次函数一次项系数为参考，分析拉伸载荷作用后磁场长度方向分量极值和法向分量梯度的影响，如图6所示。

通过分析发现，拉伸载荷对试件表面中心轴线磁场的长度方向分量极值和法向分量梯度的影响规律是一致的。当拉伸载荷在20kN以内时，长度方向分量极值和法向分量梯度值均小于0；而当拉伸载荷大于20 kN时，长度方向分量极值和法向分量梯度值接近或大于0，且随载荷的进一步增加而呈近似线性增长的规律。

图4 试件表面磁场分布

3.2 拉伸加载对磁场分布的影响

通过前面的分析可知，试件引起的附加磁场矢量可近似看作由长度方向及法向磁场分量组成，所以此处定义试件表面中心轴线上任意一点处的附加磁场矢量大小和方向为

式中：H——附加磁场矢量；

图5 不同载荷作用后的磁场分量分布

α——附加磁场矢量与中心轴线的夹角。

根据上述公式可以计算得到试件测量区域在地磁场环境下的附加磁场矢量分布规律，如图7所示。

从图中可以看出，不同拉伸加载作用后，试件表面中心轴线上磁场矢量的大小均呈现出两端大中间小的分布规律，磁场矢量与中心轴线的夹角也呈现出相同的规律，且该夹角值在轴线中心附近趋于零，其磁场矢量分布具有明显的反对称性。所以考虑到磁场矢量幅值分布的对称性，这里以中心轴线上的测量起点和终点处幅值的平均值为参考，进一步分析磁场矢量幅值在拉伸加载后的磁记忆效应，以测量轴线起点、中心和终点处磁场矢量与中心轴线的夹角为参考，分析磁场矢量方向在拉伸载荷作用后的磁记忆效应，如图8所示。

图6 长度方向磁场极值及法向分量磁场梯度的变化

从图中可以看出，在不同载荷水平的拉伸加载作用后，磁场矢量均有不同程度的变化，当拉伸加载从20kN增加至40kN时，磁场矢量的幅值及方向均发生了明显的反转。其中磁场矢量幅值在20kN以内时变化并不明显，且逐渐减小，而在20kN拉伸加载后磁场矢量幅值呈现出明显的递增趋势；在环境磁场较强的端部和较弱的中部测量区域，磁场矢量与中心轴线夹角的绝对值在20kN以内时均呈缓慢减小的趋势，然后随着载荷的进一步增加逐渐趋于一恒定值，其方向与磁场矢量初始方向相反。所以，在磁场矢量发生反转后，应力磁化对磁场矢量幅值的影响十分明显，且表现为线性增加特征，而对磁场矢量方向影响不大。

3.3 加载环境磁场下的拉伸应力磁化

图7 不同拉伸载荷作用后的磁场矢量分布

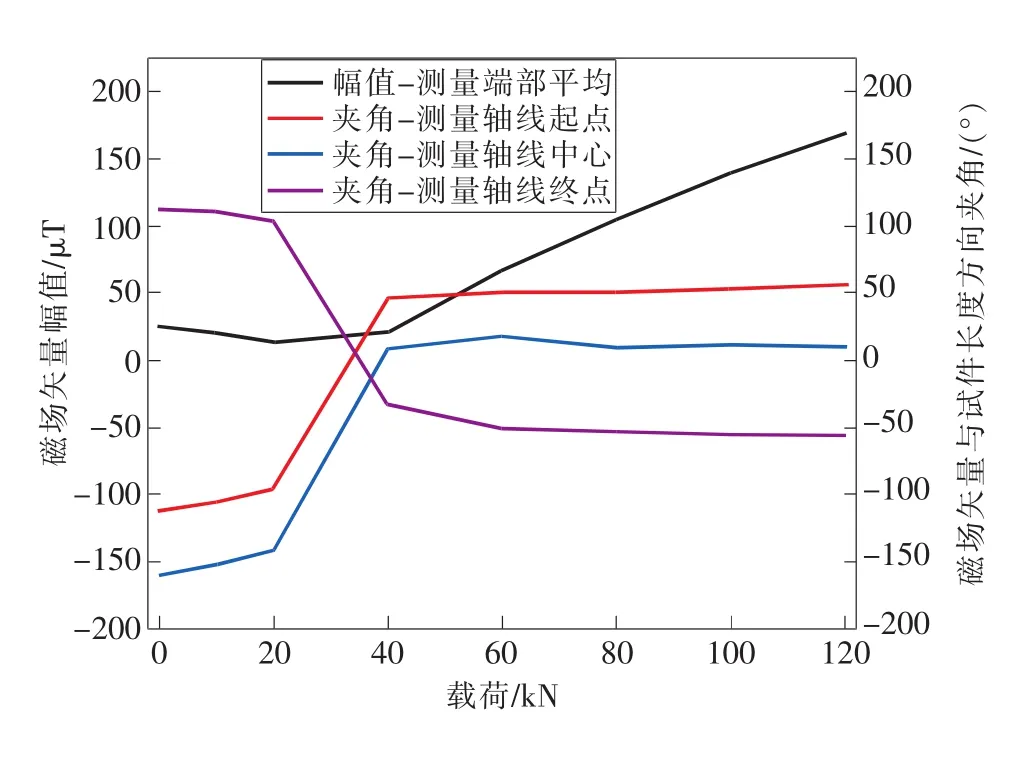
图8 磁场矢量在拉伸载荷作用后的变化

根据磁致伸缩的逆效应，在弹性应力和环境磁场的共同作用下，铁磁性材料内部的磁畴将发生可逆和不可逆的改变。所以在本实验中的每一次拉伸载荷作用后，尽管试件的应力发生了回复，但磁畴的不可逆变化却被保留了下来，表现为试件磁场的变化。根据应力等效磁场理论[11]，在外磁场作用下，拉伸应力引起的等效磁场Hσ可以描述为

式中：σ——加载应力；

μ0——真空磁导率；

λ——磁致伸缩系数；

M——磁化强度；

θ——加载应力与环境磁场矢量之间的夹角；

ν——泊松比。

该等效磁场中的磁致伸缩系数[12]可近似表示为

根据Kuruzar等[13]的研究数据，式中的γ1（0）、γ1′（0）可分别取为7×10-18m2/A2、-1×10-25m2/（A2·Pa）。将该数据代入上述式（3）、式（4）中可得：

所以应力引起的等效磁场与试件初始磁场的关系是由f（σ）g（θ）项来决定的，当f（σ）和g（θ）符号相同时，拉伸应力引起的等效磁场与试件初始磁场方向一致，会对初始磁场进行加强；反之，当f（σ）和g（θ）符号相反时，拉伸应力引起的等效磁场与试件初始磁场方向相反，会对初始磁场进行削弱。结合X80管线钢材料参数计算可知，上述公式存在影响函数f（σ）和g（θ）符号的临界值分别为σ0=70 MPa（对应拉伸载荷为17.5kN）和θ0=61.3°。在本实验中，加载环境磁场矢量在试件表面中心轴线上并不保持恒定，有着明显的分布效应，在测量区域内呈现出两端大中间小的磁场矢量分布形式，如图9所示。

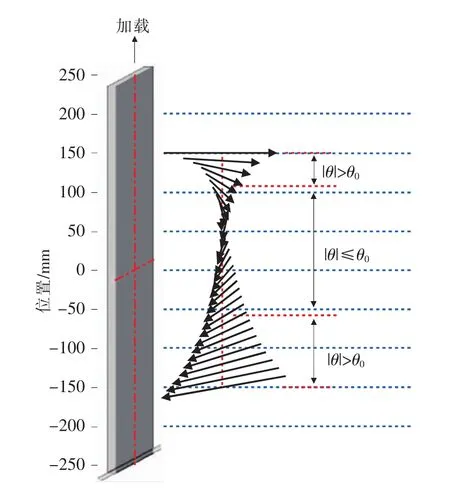
图9 试件加载时的力磁耦合环境

所以，在拉伸加载过程中，试件中心轴线上各测量点处的磁化作用并不相同，在测量区域的两端应力磁化作用较强，中心区域应力磁化作用较弱。在应力磁化较强的区域（-60～110mm以外的区域），环境磁场矢量与拉应力夹角|θ|＞θ0，所以在拉伸载荷较小（17.5 kN以内）时，f（σ）g（θ）＜0，应力磁化将导致初始磁场强度减小；在拉伸载荷较大（17.5kN以上）时，f（σ）g（θ）＞0，应力磁化将导致初始磁场强度增大。所以，在本实验拉伸载荷作用下，试件磁场矢量幅值表现为先减小后增大的变化规律，与上述理论预测的结果是基本相符的。

4 结束语

1）不同拉伸载荷作用后，试件长度方向磁场分量表现出极值特征，法向磁场分量表现为过零点特征且相交于同一点。

2）拉伸载荷对长度方向磁场分量极值和法向磁场分量梯度的影响规律是一致的，在20kN以内随载荷增大而缓慢增加，在20 kN之后随载荷增大呈近似线性增加的规律。

3）当拉伸载荷大于20kN，试件表面磁场矢量发生了磁化反转，此后随着载荷的进一步增加，试件表面磁场矢量大小呈近似线性增加，磁场矢量方向逐渐趋于恒定。所以磁化反转后的磁记忆效应主要表现为磁场矢量大小的变化，矢量方向变化不大。

[1]DOUBOV A A.Physical base of the method of metal magnetic memory[J].Nondestructive Testing of Materials and Structures，2002（42）：1-5.

[2]JILES D C，ATHERTON D L.Theory of magnetization process in ferromagnets and its application to the magnetomechanical effect[J].Journal of Physics D Applied Physics，1984，17（6）：1265-1281.

[3]JILES D C，LI L.A new approach to modeling the magnetomechanical effect[J].Journal of Applied Physics，2004，95（11）：7058-7060.

[4]WILSON J W，TIAN G Y，BARRANS S.Residual magnetic field sensing for stress measurement[J].Sensors and Actuators A，2007，135（2）：381-387.

[5]ROSLPSZ M，GAWRILENKO P.Analysis of change in residual magnetic field in loaded notched samples[J]. NDT&E International，2008（41）：570-576.

[6]WANG Z D，YAO K，DENG B，et al.Theoretical studies of metal magnetic memory technique on magnetic flux leakage signals[J].NDT&E International，2010（43）：354-359.

[7]WANG Z D，DENG B，YAO K.Physical model of plastic deformation on magnetization in ferromagnetic materials[J].Journal of Applied Physics，2011，109（1）：1-6.

[8]尹大伟，徐滨士，董世运，等.中碳钢疲劳试验的磁记忆检测[J].机械工程学报，2007，43（3）：60-65.

[9]DONG L H，XU B S，DONG S Y，et al.Variation of stress-induced magnetic signals during tensile testing of ferromagnetic steels[J].NDT&E International，2008（41）：184-189.

[10]XU M X，XU M Q，LI J W，et al.Metal magnetic memory field characterization at early fatigue damage based on modified Jiles-Atherton model[J].Journal of Central South University，2012，19（6）：1488-1496.

[11]YANG E，LI L M，CHEN X.Magnetic field aberration induced by cycle stress[J].Journal of Magnetism and Magnetic Material，2007，312（1）：72-77.

[12]LI L，JILES D C.Modeling of the magnetomechanical effect： application oftherayleigh law tothe stress domain[J].Journal of Applied Physics，2003，93（93）：8480-8482.

[13]KURUZAR M E，CULLITY B D.The magnetostriction of iron under tensile and compressive stress[J].International Journal of Magnetism，1971，1（4）：323-325.

（编辑：李妮）

The metal magnetic memory effect of X80 pipeline steel under tension load

JIA Dong，SUN Le，CHEN Yongmei，NIU Wei
（Institute of Systems Engineering，China Academy of Engineering Physics，Mianyang 621900，China）

In order to study the metal magnetic memory effect of X80 pipeline steel，the tensile loading and unloading tests and off-line magnetic field measurement of plate specimen were carried out at different load levels.Combined with the polynomial fit and vector analysis，the variations of extreme value of longitudinal component，gradient value of normal component and magnetic field vector were obtained.According to the model for equivalent magnetization of stress，the evolution of magnetic field was explained.The results show that the variation of extreme value of longitudinal component of magnetic field is consistent with gradient value of normal component，and the magnetic field vector will be reversed under coupling effects of loading environmental magnetic field and tension load.When the load is less than 20 kN，the extreme value of longitudinal component and the gradient value of normal component increase slowly，but the amplitude of the magnetic field vector and the angle between the magnetic field vector and the tension axis decrease slowly. When the load is greater than 20 kN，the extreme value of longitudinal component，the gradient value of normal component and the amplitude of the magnetic field vector increase rapidly，and the direction of the magnetic field vector tends to be not changed.

metal magnetic memory effect;stress-magnetizing;magnetic field vector;X80 pipeline steel;tension load

A

：1674-5124（2017）01-0017-06

10.11857/j.issn.1674-5124.2017.01.004

2016-05-20；

：2016-06-28

国家自然科学基金（11302206）；中国工程物理研究院科学技术发展基金（2014B04021）

贾 东（1986-），男，四川绵阳市人，助理研究员，硕士，主要从事材料力学性能及力磁耦合效应研究。