小型变体无人机动力学建模及配平分析
陈 伟,冯高鹏,拜云山
(中国工程物理研究院 总体工程研究所,四川 绵阳 621900)
小型变体无人机动力学建模及配平分析
陈 伟,冯高鹏,拜云山
(中国工程物理研究院 总体工程研究所,四川 绵阳 621900)
为了更好地分析变体无人机(Unmanned Aerial Vehicle,UAV)在变体过程中的动态响应,针对一种小型变后掠翼无人机,通过静矩来描述变体过程中重心位置的变化,推导了其六自由度非线性运动方程。变体飞机相对于固定翼飞机的运动学方程多出变体过程中引起的惯性力和惯性力矩项以及转动惯量和惯性积的微分项。利用准定常假设来简化计算变体过程中的气动力,认为在变体的任一瞬时,全机的气动力取决于该瞬时飞机的静态构型和飞行状态。从计算结果可知,在一定飞行速度和飞行高度范围内,影响气动参数的主要变量为机翼后掠角和迎角。为了确保变体飞机在变体过程中具有较理想的静稳定度,通过配平给出了不同构型时飞机重心在机体纵轴上的合理位置,有助于变体飞机控制系统设计。
变体无人机;运动方程;动态响应;配平
0 引 言
变体飞机在变体过程中,气动外形的变化必然引起飞机的转动惯量、质心位置、气动焦点位置等一系列机体特性的改变。近年来,一些学者针对特定的变体飞机进行了动力学建模与分析[1-3]。陈伟等对变后掠翼飞机进行了建模与分析[4]。乐挺等对Z型翼变体飞机进行了多体动力学建模,分析了质心位置移动和气动外形变化对变体飞机动态特性的影响,并研究了非定常效应对机翼折叠过程中气动特性的影响,认为当机翼折叠角速度较小时,可以忽略非定常气动力效
应[5-6]。Obradovic B等采用扩展刚体动力学方法得到了一种机翼可上下摆动的变体飞机的动力学方程[7-8]。Seigler T M等建立了固定于机身的机体坐标轴系,采用笛卡儿矢量描述变体飞机上各点相对于地面坐标轴系的坐标,利用达朗贝尔原理推导了变体飞机的一般动态特性[9-11]。
文中在Seigler T M等研究的基础上,推导了一种小型变体无人机的非线性运动方程。利用准定常假设来简化计算变体过程中的气动力,为了确保变体飞机在变体过程中具有较理想的静稳定度,通过配平给出了不同构型时飞机重心在机体纵轴上的合理位置,为变体飞机控制系统设计提供了基础。
1 变体飞机变体过程中的动力学建模
变体飞机在变体过程中,质心位置会发生改变,而质心速度不变。研究飞机上某固定点的速度要比质心的速度更有意义[10]。建立与机身固定的机体坐标轴系Sb-Oxyz,如图1所示。
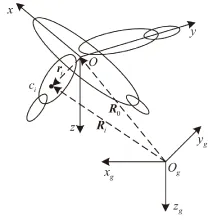
图1 坐标系
其中,Sg-Ogxgygzg为地面坐标轴系。变体飞机由μm个相互运动的部分组成,各个运动部分质量为mi,质心为ci。ri和Ri分别为ci在机体坐标轴系和地面坐标系中的坐标;R0为机体坐标轴系原点在地面坐标系中的坐标。基于以上所建立的机体坐标轴系,SeiglerTM推导了变体飞机的力方程和力矩方程[10]。
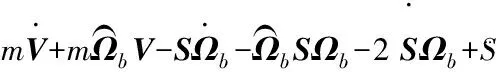
(1)
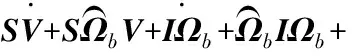
(2)
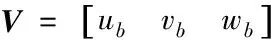
(3)
⌒为运算符,将矢量转换成反对称矩阵,有:
(4)
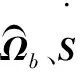
(5)
其中,Ix、Iy和Iz为绕机体坐标轴系的转动惯量;Ixy,Iyz和Izx为惯性积。
Fb为飞机受到的合外力在机体坐标轴系中的矢量。
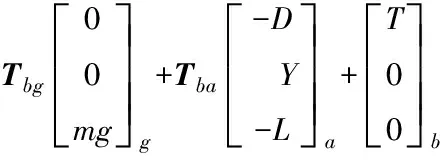
(6)
其中,Tbg为地面坐标轴系到机体坐标轴系的转换矩阵,Tba为气流坐标轴系到机体坐标轴系的转换矩阵,具体坐标系定义及转换矩阵表达式见文献[12];g为重力加速度;T为推力,与机体x轴方向平行;L为升力,Y为侧力,D为阻力;Mb为Fb产生的力矩在机体坐标轴系中的矢量:
(7)
2 六自由度非线性运动方程
基于图2所示的小型变体无人机进行研究。图2中给出了机翼后掠角为0°、30°和45°时的构型。机翼后掠角可以在0°~45°之间任意变化,与MFX-2变体飞机的机翼变形机构类似[13]。该变体飞机在机翼后掠角变化过程中,机翼宽度会按照一定的比例随着机翼后掠角一起变化,即机翼后掠角确定,机翼气动弦长和机翼面积确定,可认为变体自由度为1。在机翼后掠角最大时,机翼宽度最小。为了方便叙述,文中用机翼后掠角表示飞机构型,如机翼后掠角为0°时,简称0°构型。表1给出了变体飞机在0°构型、30°构型和45°构型时的外形参数。飞机质量m=25kg。
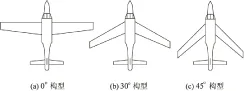
图2 变体飞机
表1中,Sw为机翼参考面积;cA为机翼的平均几何弦长;b为机翼展长。变体飞机从0°构型向45°构型变化过程中,飞机的机翼参考面积和展长逐渐减小,机翼的参考面积最大可改变36%,机翼展长最大可改变25.7%,机翼平均几何弦长最大可改变15%。
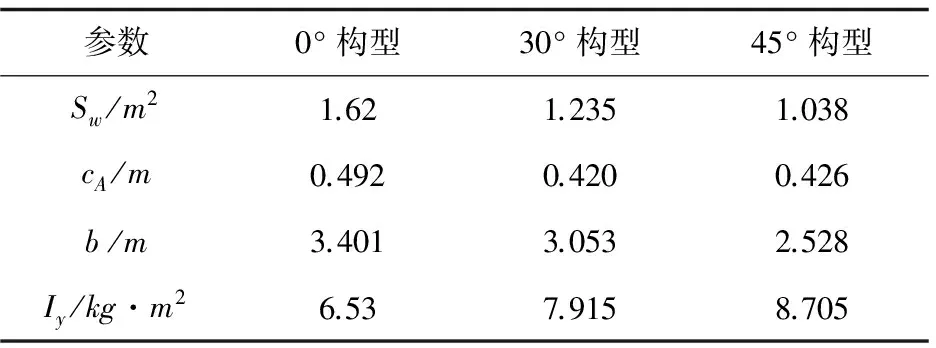
表1 变体飞机的不同构型参数
在机翼后掠角变化过程中,飞机质心和气动焦点沿机体x轴移动。设左机翼质心在机体坐标轴系中的坐标为r1=r1xi+r1yj+0k,质量为m1;右机翼质心坐标为r2=r2xi+r2yj+0k,质量为m2;机身加机尾的质心坐标为r3=r3xi+0j+0k,质量为m3。因为飞机左右对称,则有m1=m2,r1x=r2x,r1y=-r2y,Ixy=Iyz=0。飞机的转动惯量张量I为:
(8)
飞机的静矩S为:
(9)
其中,Sx≈2m1r1x+m3r3x,Sy=Sz=0,有:
(10)
将式(8)和式(10)代入式(1)和式(2)得到该小型变体飞机的力和力矩方程,按照文献[12]中推导固定翼飞机非线性运动方程的步骤,推导出变体飞机六自由运动方程:
xg=Vcosγcosχ
(11)
yg=Vcosγsinχ
(12)
(13)
(14)
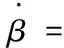
(15)
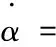
(16)
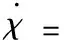
(17)
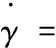
(18)
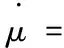
(19)
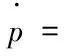
(20)
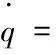
(21)
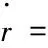
(22)
其中,xg、yg、zg为飞机在地面坐标轴系的位置分量;V为飞行速度;h为飞行高度;χ为航迹方位角;γ为航迹倾斜角;μ为航迹滚转角;α为迎角;β为侧滑角;θ为俯仰角;φ为滚转角;ψ为偏航角;FIx、FIy、FIz为变体过程引起的惯性力在气流坐标轴系中的分量,有:
(23)
MIx、MIy、MIz为变体过程引起的惯性力矩在机体坐标轴系中的分量,有:
(24)
从变体飞机运动方程来看,变体飞机相对于固定翼飞机的运动学方程多出了变体过程中引起的惯性力和惯性力矩项以及转动惯量和惯性积的微分项。在机翼后掠角变化过程中,飞机重心沿机体x轴移动,静矩Sx会随之变化。当静矩Sx不等于零时,重力相对于机体坐标轴系原点会产生力矩,在力矩方程组中分别体现在Sxgcosθsinφ、-Sxgcosθcosφ、Sxgcosθsinφ三项中。另外,在机翼后掠角变化过程中,飞机气动外形和气动焦点会发生改变,飞机的气动参数会发生较大变化。
3 不同构型的配平状态
利用准定常假设来简化计算变体过程中的气动力,认为在变体的任一瞬时,全机的气动力取决于该瞬时飞机的静态构型和飞行状态。
表2给出了在飞行速度V=25m/s、飞行高度h=1 000m、迎角α=0°时变体飞机不同构型的部分气动参数。
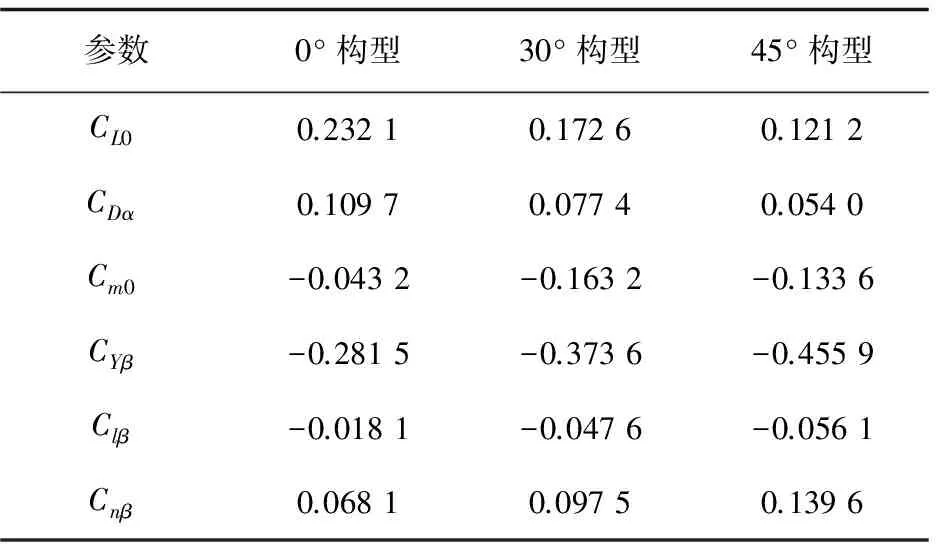
表2 变体飞机不同构型气动参数
其中,CL0为零迎角升力系数;CDα为阻力系数相对迎角的导数;Cm0为零迎角俯仰力矩系数;CYβ为侧力系数对侧滑角的导数;Clβ为滚转力矩系数对侧滑角的导数;Cnβ为偏航力矩系数对侧滑角的导数。
对于该小型变体无人机来说,由于受到发动机推力和自身设计参数的限制,飞行速度和飞行高度被限制在一定范围内,在该范围内飞行速度和飞行高度对气动参数的影响较小。主要影响气动参数的变量为机翼后掠角和迎角。图3给出了在V=25m/s、h=1 000m、δe=0°、β=0°、q=0 (°)/s时的升力系数CL、阻力系数CD、俯仰力矩系数Cm随机翼后掠角和迎角变化的拟合曲面。在迎角小于8°时,CL与迎角具有较好的线性关系,升力线斜率CLα可近似为常值,随着迎角的增大,CLα逐渐减小最终变为负值,CLα等于零对应的迎角为失速迎角。0°构型时的失速迎角在14°左右,45°构型时的失速迎角要大于16°。CD随迎角的增大而增大。在机翼后掠角变化过程中,飞机重心始终在气动焦点之前,飞机是纵向静稳定的。
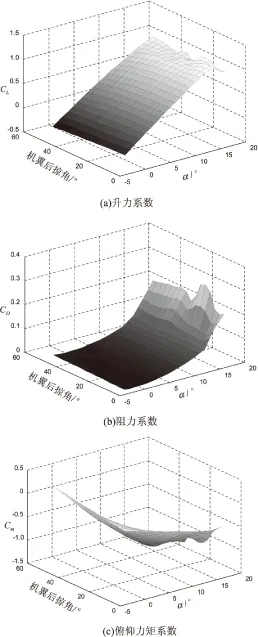
图3 气动参数随机翼后掠角和迎角变化的拟合曲面
在水平飞行状态,对变体飞机的不同构型进行配平。配平代价函数为
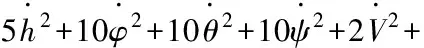
(25)
在一定的飞行速度V和飞行高度h下,通过计算配平迎角α0、配平俯仰角θ0、配平推力T0、配平升降舵偏角δe0使得代价函数值趋近于0,即飞机所受到的力和力矩平衡。由于变体飞机在变体的过程中,气动焦点在机体x轴上的位置变化较大,为了确保变体飞机具有较理想的静稳定度,随着机翼后掠角的改变应当通过配重块将飞机重心配置在合理位置上,即气动焦点在重心之后的距离与平均气动弦长的比值在10%附近。这里通过配平给出了不同构型时重心在机体x轴上相对建模原点O的位置,如表3所示,同时表3给出了在飞行高度h=1 000m、飞行速度分别为V=25m/s、V=30m/s、V=40m/s和V=50m/s时,变体飞机在0°构型、30°构型和45°构型时的配平值。
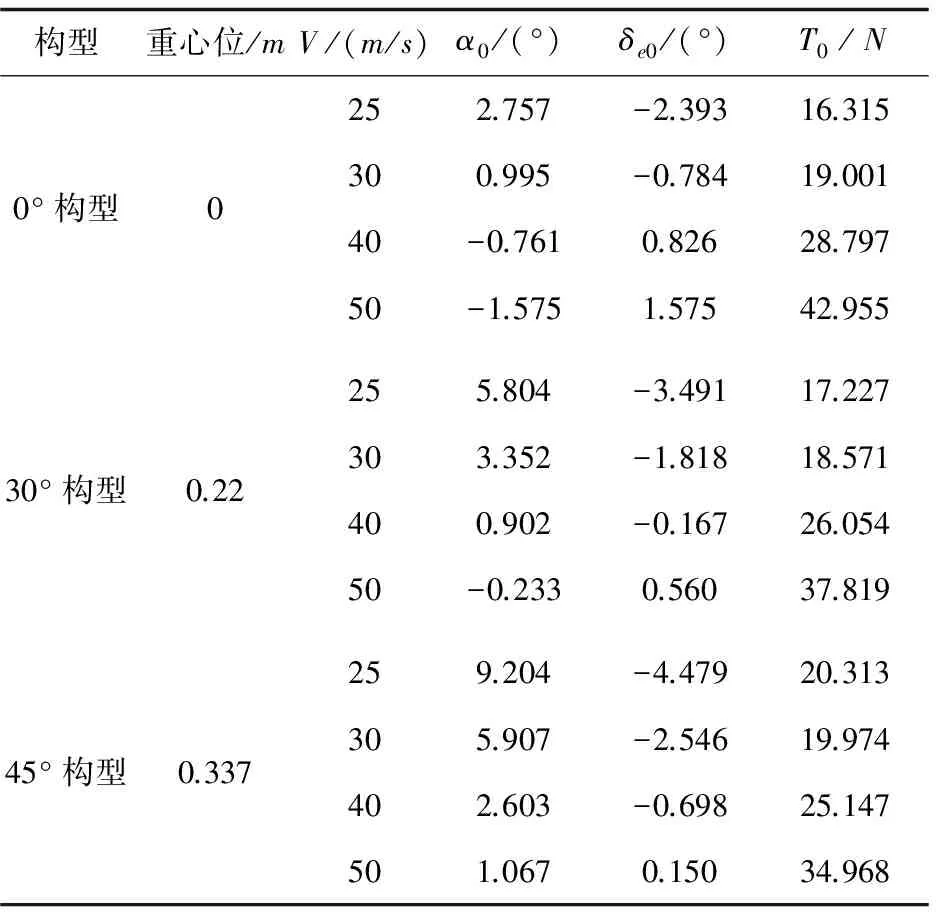
表3 配平状态
表3中,由于机翼面积随着机翼后掠角增大而减小,在飞行速度一定时为了提供相同的平飞升力,配平迎角会随着机翼后掠角增大而增大。由于配平迎角的增大,为了平衡迎角产生的低头力矩,配平升降舵偏角随着机翼后掠角增大而上偏。当飞行速度较高时,由于配平迎角较小,同时阻力系数对迎角的导数和机翼面积随着机翼后掠角增大而减小,配平推力会随着机翼后掠角增大而减小。当V=25m/s时,45°构型的配平迎角达到了9.204°,在该飞行速度下做机动动作时迎角可能会达到失速迎角,表明45°构型不适合在低速下飞行。根据以上分析可知,在低速巡航时,为了使升阻比最大,增大巡航时间,可采用0°构型或者小后掠角构型飞行;在快速进入战区或逃离战区时,为了减小飞行阻力,可采用45°构型飞行。
4 结束语
文中推导了一种变后掠翼无人机的非线性运动方程。利用准定常假设来简化计算变体过程中的气动力,认为在变体的任一瞬时,全机的气动力取决于该瞬时飞机的静态构型和飞行状态。为了确保变体飞机在变体过程中具有较理想的静稳定度,通过配平给出了不同构型时飞机重心在机体纵轴上的合理位置。为了确保变体过程中的飞行稳定性,所设计的飞行控制系统应当较好地抑制重心位置变化带来的影响。
[1] 陈 伟,卢京潮,王晓光,等.基于backstepping/RHO的变体飞机控制器设计[J].北京航空航天大学学报,2014,40(8):1060-1065.
[2] 陈 伟,卢京潮,章卫国.基于LQ/RHO多回路技术的变体飞机控制器设计[J].北京航空航天大学学报,2013,39(3):290-294.
[3] 陈 伟,卢京潮,刘志君,等.基于指令滤波器的变体飞机RHO控制器设计[J].飞行力学,2014,32(5):423-426.
[4] 陈 伟,冯高鹏.变体飞机建模及自适应动态面控制[J].测控技术,2016,35(2):91-95.
[5] 乐 挺,王立新,艾俊强.Z型翼变体飞机的纵向多体动力学特性[J].航空学报,2010,31(4):679-686.
[6] 乐 挺,王立新,艾俊强.变体飞机设计的主要关键技术[J].飞行力学,2009,27(5):6-10.
[7]ObradovicB,SubbaraoK.Modelingofflightdynamicsofmorphing-wingaircraft[J].JournalofAircraft,2011,48(2):391-402.
[8]ObradovicB,SubbaraoK.Modelingofdynamicloadingofmorphing-wingaircraft[J].JournalofAircraft,2011,48(2):424-435.
[9]SeiglerTM.Dynamicsandcontrolofmorphingaircraft[D].Virginia:theVirginiaPolytechnicInstituteandStateUniversity,2005.
[10]SeiglerTM,NealDA,BaeJS,etal.Modelingandflightcontroloflarge-scalemorphingaircraft[J].JournalofAircraft,2007,44(4):1077-1087.
[11]SeiglerTM,NealDA,InmanDJ.Dynamicmodelingoflarge-scalemorphingaircraft[C]//AIAAstructures,structuraldynamics,andmaterialsconference.Newport:AmericanInstituteofAeronauticsandAstronautics,2006:3668-3678.
[12] 吴森堂.飞行控制系统[M].北京:北京航空航天大学出版社,2005:20-70.
[13]GandhiN,CooperJ,WardD,etal.Ahardwaredemonstrationofanintegratedadaptivewingshapeandflightcontrollawformorphingaircraft[C]//AIAAguidance,navigation,andcontrolconference.Chicago:AmericanInstituteofAeronauticsandAstronautics,2009.
Dynamics Modeling and Trimming Analysis for Small Morphing UAV
CHEN Wei,FENG Gao-peng,BAI Yun-shan
(Institute of Systems Engineering,China Academy of Engineering Physics,Mianyang 621900,China)
In order to better analyze the dynamic response of morphing Unmanned Aerial Vehicle (UAV),the moving of the center of gravity is described by quiet moment,and the six free nonlinear equations of motion for a small variable sweep UAV is derived.The kinematic equation of morphing aircraft has more items that are inertial force and inertial moment than fixed wing plane.The aerodynamic forces and moments in the process of morphing are calculated with the quasi-steady assumption,the aerodynamic force is depended on the static configuration and flight state of morphing aircraft at the moment of morphing.From the results it can be known that the main variable that affects the aerodynamic parameters ie sweep angle and angle of attack within a certain range of flight speed and altitude.To make sure that the morphing aircraft has an ideal static stability margin,the responsible position of the center of gravity on the longitudinal axis of the body at different configurations is obtained by trimming,which lays a foundation for the control system design for the morphing aircraft.
morphing UAV;equations of motion;dynamic response;trimming
2016-03-26
2016-06-29
时间:2017-01-04
国家自然基金联合基金(U1430113);中国工程物理研究院科学技术发展基金(2014B0101009)
陈 伟(1986-),男,博士,工程师,研究方向为制导武器控制系统设计;冯高鹏,通讯作者,高级工程师,研究方向为武器系统设计。
http://www.cnki.net/kcms/detail/61.1450.TP.20170104.1039.068.html
TP273
A
1673-629X(2017)02-0125-05
10.3969/j.issn.1673-629X.2017.02.028

