同态加密的分布式K均值聚类算法研究

姚禹丞，宋 玲，鄂 驰

(广西大学 计算机与电子信息学院，广西 南宁 530004)

同态加密的分布式K均值聚类算法研究

姚禹丞，宋 玲，鄂 驰

(广西大学 计算机与电子信息学院，广西 南宁 530004)

针对分布式环境下多方联合执行K均值聚类挖掘任务过程中存在的安全性问题，如潜在的合谋攻击和窃听攻击导致隐私泄露和敏感知识被发现，提出了一种隐私保护算法(PPDK)。在数据对象水平分布的情况下，该算法利用同态加密的思想，设计了一种新的加密机制。通过改进加密密钥的生成方式，使得参与计算的各方持有不同的密钥，对于产生的密文，其他参与方无法解密，并且在计算过程中所有的加密解密操作均由各参与方独立完成，因此可以限制半诚实的参与方试图窃听其他参与方的私有信息，以及与中心站点合谋揭露隐私的可能性。通过理论分析和实验结果表明，在有效的时间内，PPDK算法可以在确保分布式K均值聚类挖掘任务得到正确结果的前提下，很好地保护数据的隐私性。

分布式；K均值聚类；同态加密；隐私保护

0 引 言

随着计算机网络和数据库技术的发展，许多组织和机构收集和存储了大量数据，这些数据背后蕴含着很多重要的信息而且大部分都按地理位置分布于多个场所。为了更好地利用这些数据，人们希望对其进行更深层次的分析。利用数据挖掘[1-4]技术可从这些数据中提取有价值的知识，但在分布式场景下，数据挖掘任务需要通过多方之间的合作来完成。

传统的集中式数据挖掘无法胜任，首先将所有存储在各个地方的数据放到一个中心进行挖掘是不可能的，其次在双方或多方合作进行数据挖掘时，出于数据库可能含有敏感的隐私或者商业价值的顾虑，参与者往往不愿意将数据与他人共享而只愿共享数据挖掘的结果，这种情况在科学研究、医学研究及经济和市场动态研究等方面屡见不鲜。这就要求提出在分布式环境下能保持隐私性的数据挖掘算法。对于参与者而言，只能获得最终的挖掘结果，除此以外，不能获得其他人的任何信息。

为了解决多方合作进行聚类挖掘时带来的隐私泄露和敏感知识被发现的问题,提出了越来越多的分布式算法。在分布式环境下，参与者根据其行为可分为准诚信攻击者和恶意攻击者。准诚信攻击者是遵守相关计算协议但仍试图进行攻击的站点；恶意攻击者是不遵守协议且试图披露隐私的站点。而分布式的数据集有两种划分方法：基于水平的划分和基于垂直的划分。基于水平的划分是每个站点都存储着全部数据对象的一个子集，且这些子集之间没有交集。基于垂直的划分则使得每个站点都存储着所有数据对象全部属性的一个子集，且子集之间没有交集。

K均值是经典的基于距离划分的聚类算法，其具有简单高效的特点，在很多领域都得到了广泛应用。文中假设所有站点为准诚信攻击者，并在水平划分的数据集上进行隐私保护的K均值聚类算法的研究。为了解决目前分布式K均值聚类算法中还存在的隐私泄露的问题，设计了一种可以独自生成私有密钥的同态加密算法，同时采用主从两级节点的分布式计算模型来保证数据挖掘任务准确高效的执行。

1 相关工作

众多分布式环境下基于隐私保护的数据挖掘应用都可以抽象为安全多方计算(SecureMulti-partyComputation，SMC)的模型，SMC是近年来在信息安全与分布式计算领域迅速崛起的一个活跃的研究方向。它能够保证参与计算的多方在各自的输入信息不泄露的前提下获得合作计算的结果，这正好符合分布式数据挖掘中隐私保护的要求。文献[5]利用把私有数据划分成n份并分发给其他参与方的思想，设计了安全多方求和协议和安全多方求平均值协议，使用该协议可以保证在水平分布或垂直模型中当其余所有参与方合谋时，剩下一方的私有数据才受到威胁。文献[6]引入一个半可信第三方，将本地数据和扰乱后发送给半可信第三方可以实现安全求和与安全求平均值，该算法在保证隐私的前提下减少了各参与方之间的通信量。

基于数据加密的隐私保护技术可以实现通讯的安全性以及对私有数据的保护，因此其多用于分布式应用中。在隐私保护数据挖掘算法中，SMC可以看成是基于加密技术的一个特例。2009年，GraigGentry提出基于理想格的完全同态加密技术(FullyHomomorphicEncryption,FHE)。如果一种加密算法对加法和乘法都能找到其对应的同态操作，即满足e(m1)⊕e(m2)=e(m1⊕m2)，则称其为全同态加密算法。目前，基于同态加密的分布式隐私保护数据挖掘已经取得了丰富的研究成果。文献[7]基于同态加密和安全置换的算法，实现了在垂直划分下隐私保护的K-means聚类。文献[8]提出了一种完全同态加密的分布式聚类挖掘算法。文献[9]基于全同态公钥加密协议和数据扰乱方法，设计了一个安全比较协议。文献[10-11]分别使用了Paillier公钥加密机制[12]和ElGamal加密机制[13]，同样具有同态的性质。文献[14]设计了一个加密方案用以提供云计算环境中的隐私保护。文献[15]基于椭圆曲线的同态加密消除了SMC中的可信第三方。

2 问题描述

2.1 合谋攻击

在多个参与方合作进行分布式聚类挖掘任务时，存在信息泄露的问题。利用同态加密技术可以保证参与计算的多方在各自输入信息不泄露的前提下获得合作计算的结果。但是在对以往分布式隐私保护聚类算法的研究中发现，若使算法中的中心站点(SP)，即半可信的第三方，对中间计算结果进行解密，这将对数据隐私构成威胁。因为在现实中很难找到可信的第三方，无法保证合谋的情况下私有数据不被泄露，如图1所示。

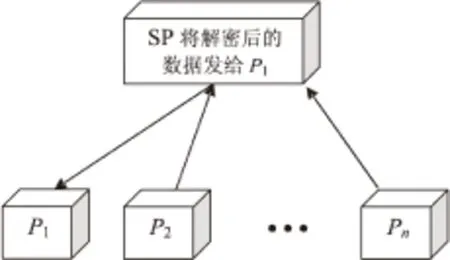
图1 中心站点SP与P1合谋的情况

2.2 窃听隐私

此外，以往算法还不具备防窃听的能力。参与分布式聚类计算的各方利用同态加密算法对私有数据进行加密，各参与方可使用相同的密钥P解密。由于相互之间不通信，可以保证各自的隐私。但若某参与方(如P1)窃听了他方的发送数据，便可使用共有密钥P对他方的数据进行解密，从而暴露了隐私，如图2所示。

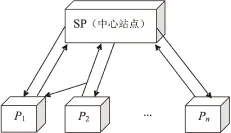
图2 P1窃听其他参与方的情况

3 基于改进同态加密的隐私保护分布式K均值算法

针对以上问题，基于同态加密算法设计了一种新算法(PPDK)，可以在参与方数n≥3的情况下保证隐私的安全。其基本思想是:利用改进的同态加密算法，对分布式K均值算法中出现的敏感数据进行加密，使得中心站点只负责计算密文的和，所有的加密解密过程全由局部站点执行。改进后加密算法中的密钥(P,ri)有两个参数，其中P为一个大数，ri≪P(i=1,2,…,n;n≥3)为各参与方生成的随机数，且值不相同，改进后的算法仍满足同态加密的性质。由于各参与方的加密密钥不同，使得在联合计算中即使出现合谋或者窃听的情况也能保证密文不被解密。

3.1 改进的同态加密算法

基于同态加密思想，提出了一种新的加密算法，该算法满足e(m1)+e(m2)=e(m1+m2)。

(1)算法主要步骤。

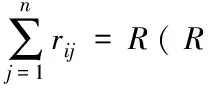
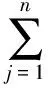
③Pi选择一个大数P作为密钥的一个参数，再各自选择一个随机数qi，最后对扰乱后的数据加密。

(1)

D(E(di))=(E(di)modP)-nR

(2)

(2)算法的同态性质的证明。

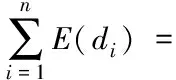
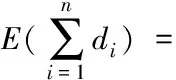
3.2 PPDK算法

输入:各站点Pi的数据集为Di(i=1,2,…,n;n≥3)，每个Di对象个数为mi(i=1,2,…,n;n≥3)，聚簇个数为k。

输出:k个最终聚簇。

(1)PPDK算法-中心站点。

①中心站点SP随机产生k个初始聚簇中心cj(j=1,2,…,k)以及随机数R，并发送到从站点Pi。

③直到每个聚类不再发生变化。

(2)PPDK算法-局部站点。

①各局部站点Pi(i=1,2,…,n;n≥3)根据中心站点发来的初始聚簇中心cj(j=1,2,…,k)，计算其与本站点数据集Di包含的mi(i=1,2,…,n;n≥3)个对象的欧氏距离，确定每个对象所属的类。

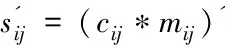
④直到每个聚类不再发生变化。

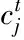
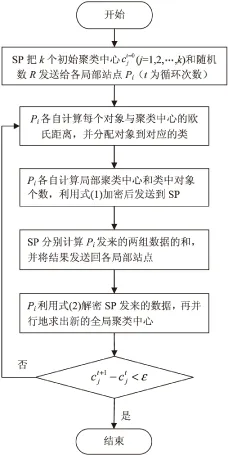
图3 PPDK算法流程图

4 算法理论分析及实验

文中对同态加密的密钥引入了一组随机数的和作为密钥的另一个参数，对于涉及到数据隐私的以下几方面，该算法都具有保护性：(1)联合计算过程中各站点数据的安全性；(2)通信过程的安全以及防窃听性；(3)合谋情况下数据隐私的安全性。加密解密过程会增加算法的时间复杂度，但由于算法本身时间复杂度不高，其增加在可以容忍的范围之内。

4.1 安全性分析

(1)联合计算过程中各站点数据的安全性。

由于各站点输入的是加密后数据，保证了在联合计算时各站点的私有信息不被泄露，并且整个计算过程的加密解密操作全由各站点独立完成，所以可以保证在联合计算过程中各站点数据的安全性。

(2)通信过程的安全以及防窃听性。

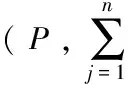
(3)合谋情况下数据隐私的安全性。

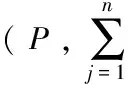
4.2 聚类精度分析

PPDK算法是对局部聚类中心进行加密，但保留了分布式K均值聚类的迭代过程。分布式K均值聚类算法结果的差异性在于初始聚类中心的选取方式和距离的计算方式，PPDK算法没有修改两者，且迭代过程依然是从第一次迭代到最终次迭代不断修正聚类中心，所以算法的正确性得到保证。

文中通过计算所有对象与其所属聚簇的聚类中心的欧氏距离和来评价聚类的精度。

(3)

其中，k为聚类的簇数；mj为第j个聚簇内的对象数；dji为第j个聚簇内第i个对象；cj为第j个聚簇的聚类中心。Precision的值越小说明聚类结果越好。

4.3 时间复杂度分析

从图3可知，PPDK的时间复杂度为O(ktm+ktn)。其中，k为聚簇数，t为循环次数，m为数据集的数据对象总数，n为参与方的个数。由于加密解密过程的存在增加了算法的时间复杂度，每次循环其时间复杂度为O(kn)，但同态加密算法本身的复杂度为常数级，因此相比于无隐私保护的分布式K均值挖掘过程，PPDK计算时间的增加在可容忍的范围之内。

4.4 实验与结果分析

文中算法用Java语言实现，在一台计算机上模拟3个局部站点，使用RMI(Remote Method Invocation,远程方法调用)实现站点间的通信。实验运行环境为：Intel(R) Core(TM) i5-4 200 M CPU @ 2.50 GHz 2.50 GHz 4.0 GB/Windows7。

对UCI机器学习数据集中的3个数据集进行了对比实验，如表1所示。

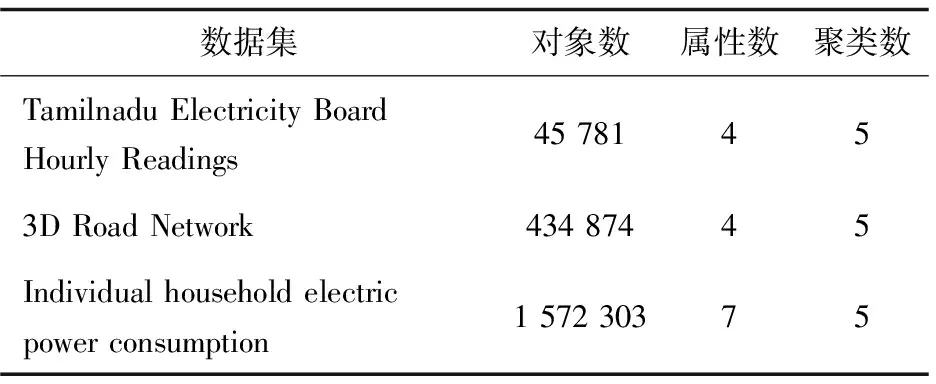
表1 UCI机器学习数据集

需要说明的是，随机选取的初始聚类中心会使算法的执行时间具有不确定性。这里阈值ε=0.01，实验结果取10次运行的平均值，见图4和图5。

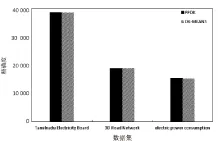
图4 算法聚类精度对比

从图4可见，PPDK算法的聚类精度与DK-MEANS算法保持一致。图5显示PPDK执行时间略高于DK-MEANS，这是因为加密解密过程额外增加了算法的执行时间，但为线性增长。

5 结束语

文中针对分布式环境提出了一种保护隐私的聚类挖掘算法—PPDK。该算法基于同态加密算法，使得各

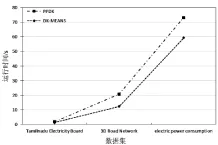
图5 算法运行时间对比

参与方拥有不同的密钥，从而避免合谋攻击和窃听攻击。理论分析和实验结果表明，PPDK能在保持挖掘结果精确度的同时防止各参与方隐私数据的泄露，且时间增加在可容忍的范围内。

[1]HanJW，MichelineK.数据挖掘概念与技术[M].范 明，孟晓峰，译.北京：机械工业出版社，2012.

[2] 周水庚，李 丰，陶宇飞，等.面向数据库应用的隐私保护研究综述[J].计算机学报，2009，32(5):847-861.

[3]PrakashM,SingaravelG.Areviewonapproaches,techniquesandresearchchallengesinprivacypreservingdatamining[J].AustralianJournalofBasic&AppliedSciences,2014,8(10):251-259.

[4] 郑苗苗,吉根林.DK-Means—分布式聚类算法K-Dmeans的改进[J].计算机研究与发展,2007,44(s2):84-88.

[5] 杨丹凤,余青松,郑冀之.分布式数据隐私保护K-均值聚类算法[J].计算机与数字工程,2008,36(7):113-116.

[6] 张国荣,印 鉴.分布式环境下保持隐私的聚类挖掘算法[J].计算机工程与应用,2007,43(18):165-167.

[7]VaidyaJ,CliftonC.Privacy-preservingk-meansclusteringoververticallypartitioneddata[C]//NinthACMSIGKDDinternationalconferenceonknowledgediscovery&datamining.[s.l.]:ACM,2003:206-215.

[8] 刘英华,杨炳儒,曹丹阳,等.分布式聚类算法的隐私保护研究[J].计算机科学,2012,39(3):160-162.

[9] 方炜炜,杨炳儒,夏红科.基于SMC的隐私保护聚类模型[J].系统工程与电子技术,2012,34(7):1505-1510.

[10]ErkinZ,VeugenT,ToftT,etal.Privacy-preservingdistributedclustering[J].EURASIPJournalonInformationSecurity,2013,2013(1):1-15.

[11]YiX,ZhangY.Equallycontributoryprivacy-preservingk-meansclusteringoververticallypartitioneddata[J].InformationSystems,2013,38(1):97-107.

[12]PaillierP.Public-keycryptosystemsbasedoncompositedegreeresiduosityclasses[C]//Internationalconferenceontheoryandapplicationofcryptographictechniques.[s.l.]:Springer-Verlag,1999:223-238.

[13]ElgamalT.Apublickeycryptosystemandasignatureschemebasedondiscretelogarithms[J].IEEETransactionsonInformationTheory,1985,31(4):469-472.

[14] 黄汝维,桂小林,余 思,等.云环境中支持隐私保护的可计算加密方法[J].计算机学报,2011,34(12):2391-2402.

[15]PatelSJ,ChouhanA,JinwalaDC.Comparativeevaluationofellipticcurvecryptographybasedhomomorphicencryptionschemesforanovelsecuremultipartycomputation[J].JournalofInformationSecurity,2014,5(1):12-18.

Investigation on DistributedK-means Clustering Algorithm of Homomorphic Encryption

YAO Yu-cheng,SONG Ling,E Chi

(College of Computer and Electronic Information,Guangxi University, Nanning 530004,China)

Aiming at security problems in the process of multi parties performingK-meanclusteringminingtaskunderdistributedenvironment,suchaspotentialcollusionattacksandeavesdroppingattacksleadingtoprivacydisclosureandsensitiveknowledgetobefound,aprivacyprotectionalgorithm,PPDK,isproposed.Inthecaseofthehorizontaldistributionofthedataobjects,thisalgorithmhasdesignedanewencryptionmechanismbasedontheideaofthehomomorphicencryption.Byimprovingthegenerationoftheencryptionkey,itmakeseachpartiesholddifferentkeys.Onepartycan’tdecrypttheciphergeneratedbyotherparties.Andintheprocessofcalculating,allencryptionanddecryptionoperationsareexecutedbytheparticipantsindependently.Therefore,itcanlimitthepossibilityofsemihonestpartiestryingtoeavesdroptheotherparties’privateinformationandconspirewithcentersite.Theoreticalanalysisandexperimentalresultsshowthatwithintheeffectivetime,PPDKalgorithmcanensurethatthedistributedK-meansclusteringminingtasksgetacorrectresults,andtheprivacyofthedatahasaverygoodprotection.

distributed;K-means;homomorphicencryption;privacyprotection

2016-04-01

2016-07-06

时间：2017-01-10

广西自然科学基金项目(2013GXNSFAA253003)

姚禹丞(1988-)，男，硕士研究生，研究方向为数据挖掘；宋 玲，教授，研究方向为网络信息安全。

http://www.cnki.net/kcms/detail/61.1450.TP.20170110.1019.052.html

TP

A

1673-629X(2017)02-0081-05

10.3969/j.issn.1673-629X.2017.02.019