光栅传感器信号精细分方法的探究

刘泊　高海霞　邹峰　王明星

摘要：光栅传感器信号精细分中细分误差较大的问题，提出一种新的精细分设计方法——A/D采样重构法，来实现精细分，该方法构造的函数与其线性函数之间的理论误差最大不超过0.3%，并在实际测量中与传统的正切法相比，可判断该方法能有效的解决了信号输出非线性较大的问题。

关键词：光栅传感器；精细分；重构法

DOI：10.15938/j.jhust.2016.06.007

中图分类号：TN911.7

文献标志码：A

文章编号：1007-2683（2016）06-0035-04

0.引言

精密测量技术与我们的生活息息相关，不但在仪器制造、机械生产，武器研制等方面发挥着重要的作用，它更是衡量一个国家科技水平发展的一个标尺，计量光栅作为精密测量的元件，已被广泛的运用，然而，我国的计量光栅技术发展水平还不够完善，难以到达精密测量的要求。

因此，需要对器件输出的信号进行细分来满足精密测量对精度的要求，由于光栅传感器输出的莫尔条纹信号近似为正余弦信号，该正余弦函数是与相位和空间位移——对应的，因此，可以通过对光栅传感器输出的莫尔条纹信号进行细分，来实现精密测量的目的。

光栅传感器实现精密测量的原理是：在使用CPLD对光栅传感器输出的正余弦信号进行N倍细分的同时，对小于1/N栅距的位移进行A/D采样实现更高次的细分。可见，在莫尔条纹信号细分过程中高次细分为重中之重，是决定整个系统分辨力的关键因素。

但在莫尔条纹信号细分过程中高次细分过程中，近似为正弦波的莫尔条纹在90°和270°附近线性很差，变化率很小，直接进行A/D采样会带来难以控制的误差，因此需要将正弦波转化为线性度较好的三角波，这样就会减少误差，从而提高测量精度。

本文设计了A/D采样重构法来实现将正弦波转化为三角波，因该方法是通过A/D对莫尔条纹进行采样，而后重新构造函数，故命名为A/D采样重构法.通过在理论分析和实际测量等方面与传统的正切法相比较，来判断A/D采样重构法在精细分过程中的是否更具优异性。

1.精细分实现方法的原理分析

正余切函数经过上面的变换之后，构造成一个新的函数u_A/u_A的matlab仿真图如图1所示.

2.两种方法仿真误差的计算与分析

2.1正切法理论误差计算与分析

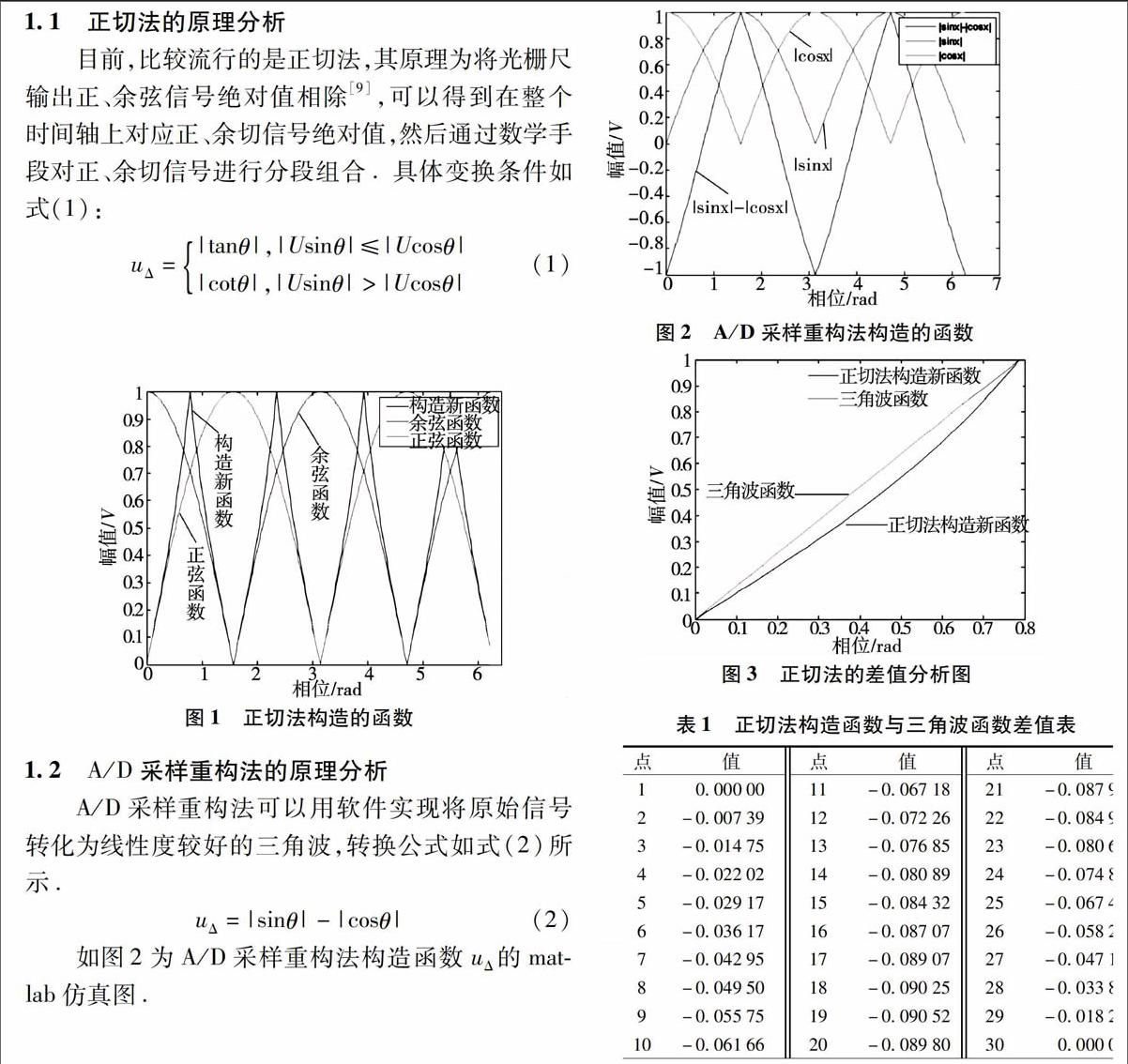
图3为用MATLAB软件对正切法进行的差值分析的图，由该图可进行正切法的线性误差进行分析：正切法构造的新函数比三角波函数线性度差很多，因此，在理论上会使得精细分的误差较大。

接下来通过对正切法构造的函数进行随机采样，比较各个采样点与三角波函数上对应点差值的大小来进一步说明正切法的准确性如何。

表1为随机选取的30个点得正切法构造函数与三角波函数在对应点的差值，对表中的数据求平均得Arv=-0.05670；对表中的数据求方差得Var=0.00088；对表中的数据求最大值得Mix=0.09052。

由计算出的结果可知，正切法所构造的函数与三角波函数的误差较大，这样就会在细分原理上造成较大的误差，进而降低了整个系统的测量精度，因此需要一种较正切法更好的一种细分方法来实现精密测量，对此本文提出了A/D采样重构法来减少在细分原理上的误差。

由结果可知，A/D采样重构法构造的函数与其线性函数之间的误差最大不超过0.3%，即将该方法的构造函数来进行细分时，细分原理上引入的最大误差不超过0.3%。

接下来通过MATLAB来实现显示与计算A/D采样重构法的构造函数与三角波函数的理论误差。图4为用MATiAB软件对A/D采样重构法进行的差值分析图，由图可以明显的看出：A/D采样重构法构造的新函数与正切函数线性度线性误差较小.与正切法相比，A/D采样重构法线性度好得多，因此，理论上，在精细分过程中，A/D采样重构法比正切法带来的误差较小。

接下来通过对A/D采样重构法构造的函数进行随机采样，比较各个采样点与三角波函数上对应点差值的大小来进一步说明该方法的准确性如何，

表2为随机选取的30个点得A/D采样重构法函数与三角波函数的差值计算值。

对表中的数据求平均值得Arv=-0.02645；对表中的数据求方差得Vat=0.00019；对表中的数据求最大值得Mix=0.04214。

借用MATLAB软件，通过比较两种方法的构造函数与三角波函数之间的差值的平均值、方差和最大值等，可得A/D采样重构法的构造函数的理论误差明顯好于正切法的构造函数。

3.两种方法实际测量误差的计算与分析

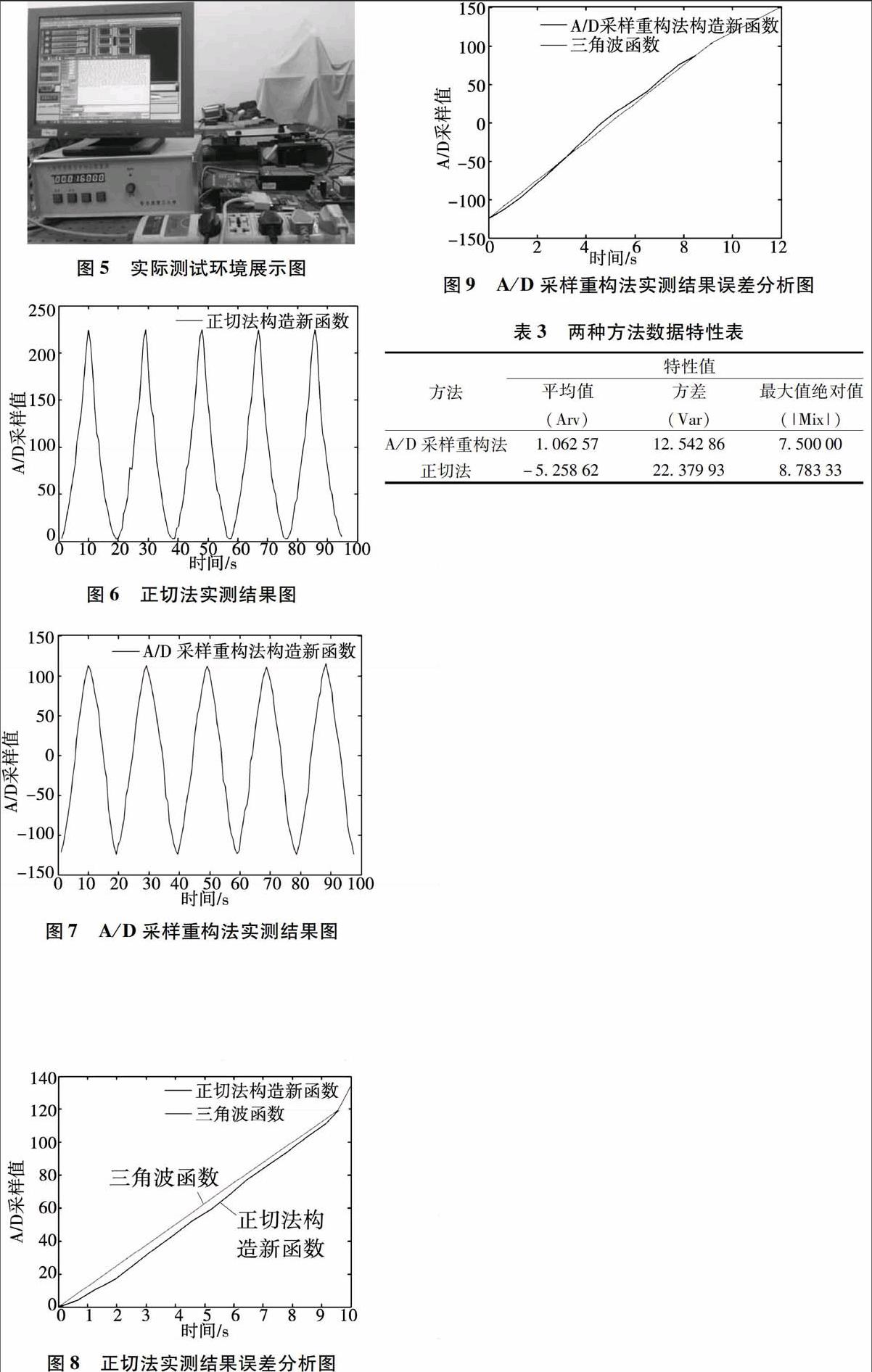
通过具体的实际测试来对两种方法的误差进行计算分析，实验环境的搭建是通过具有匀速性的电机作用于光栅传感器（如图5），然后分别用两种方法对产生的莫尔条纹进行处理，接着单片机将数据通过串口输送给计算机，最终由计算机对数据显示、处理并进行误差分析。

通过实际测试，将两种方法所得到的数据分别进行展示（如图6、7），得到的结果分别如图所示：

接下来，分别针对两种方法进行测量所得到的数据进行误差分析，借助MATLAB软件，可以分别得到两种方法的误差分析图（如图8、图9）。

同样可以得到数据在对应点的线性误差值，分别对两种方法求平均值、方差、最大值绝对值，结果如表3。

通过表3可以清楚的看到，A/D采样重构法与三角波的近似度明显好于正切法。

4.结论

本文分别在平均值、方差、最大值绝对值等方面，分析两种方法与三角波函数在线性度方面的误差，得出A/D采样重构法比正切法线性度好得多，这样在A/D对构造的函数进行采样的过程中可以有效的减小细分原理上的误差，因此更适用于光栅传感器信号精细分系统的设计。