瓦特型六杆机构的简化函数综合法

孙永国　冀文雨　张庭　杜明伟　纪培国　王磊

摘要：针对瓦特型六杆机构优化困难的问题，基于六杆机构简化函数综合原理，采用层叠目标优化算法，对瓦特型六杆机构进行分析，建立数学模型，给出了优化算法流程，并进行了实例计算、仿真分析，结果表明层叠优化算法适用于求解瓦特型六杆机构，将六杆机构拆为四杆机构和二杆机构这种方法是可行的，仿真数据表明误差控制在很0.4mm的范围内，证实了该方法正确有效，为研究对六杆机构综合提供了新的思路和方法。

关键词：瓦特型六杆机构；简化函数综合；四杆机构；二杆机构；层叠优化算法

DOI：10.15938/j.jhust.2016.06.006

中图分类号：THll2

文献标志码：A

文章编号：1007-2683（2016）06-0028-07

0.引言

瓦特型六杆机构是平面六杆机构的一个大类，在工程中具有重大的应用价值.应用瓦特型六杆机构的游梁式抽油机，输出杆的摆角是原抽油机的4倍，使抽油机冲程大为增加，提高了其性能，由于平面六杆机构较四杆机构可实现更多的精确点，从而更好的满足实际设计的需要.国内外许多学者对平面六杆机构函数综合做了大量研究。

连杆机构简化综合的核心就是将多个设计参数分成少数的几组分别进行综合，借助计算机解算技术，将机构运动综合问题归结为求解多变量约束优化问题求解，目前国内对六杆机构的研究主要涉及的是史蒂芬森型六杆机构的研究，而对于瓦特型六杆机构的函数综合的研究还不是很深入，康利君利用ADMAS仿真得到了瓦特型六连杆机构的运动情况，同时应用ANYSYS软件对摇臂构件进行了模态分析。

杨捷将Matlab和数值解法运用在平面机构的设计及优化当中，提升了机构优化设计的速度和精确程度，潘敏介绍了四杆机构和六杆机构在焊装家具中的应用，并简化了夹具的结构。

陈平详细的研究了平面连杆机构尺度综合专家系统的主框架、知识库和推理机，黄康对平面连杆机构计算机辅助设计系统进行了开发，对常用的平面连杆机构进行运动分析及综合，张建军将平面六杆机构间歇函数综合优化模型的设计参数减少为4个，并建立了平面六杆机构间歇函数综合的优化模型，并将求解问题转化为鞍点规划模型，利用BFGS方法和遗传算法结合求解。

李景雷文提出的平面六杆双间歇机构近似函数综合思想，编制了一套平面六杆双间歇机构近似函数综合以及仿真软件，并进行了实例计算，钱志良以主动曲柄和从动摆杆问的给定运动关系为基础，通过引入二自由度五杆机构及其连杆铰接点曲线，提出函数插值轮换综合法。

隆飞通过调节连杆的位置来实现多函数的平面六杆瓦特型可调机构及其综合方法，吴努提出了利用Roberts定理设计六连杆平动引导机构的思路，介绍了几何解析法确定引导机构几何尺寸的方法，傅伟成提出一种用于内燃机的新型曲柄连杆机构，建立了该机构的运动学数学模型，并编制了计算机程序。

苏和平分析了安装角、偏转角、偏距对一种瓦特Ⅱ型机构的影响，韩建友给出了Watt-I型六杆机构尺寸综合的一种新方法，该方法对于刚体有限分离问题通过建立机构解域，最终能够得到满足给定设计条件的全部可行解，但该方法求解复杂，计算时间较长。

本文将瓦特型六杆机构拆分为四杆机构和二杆机构，建立数学模型，提出层叠目标优化算法，用于求解给定问运动的平面六杆机构综合问题，最终实现瓦特型六杆机构的简化函数综合。

1.瓦特型六杆机构综合模型

1.1瓦特型六杆机构的机构类型

瓦特型六杆运动链是一种具有相邻的三副杆的六杆转动副运动链，也称为Watt链，Watt型六杆机构的基本形式，如图1示，以不同构件作为机架，可以得到两种watt型六杆机构，即Watt-I型和watt-Ⅱ型，如图2和3所示，限于篇幅，本文针对Watt-I型六杆机构进行分析。

1.2瓦特型六杆机构坐标

标定运动副节点的Watt-I型六杆机构，如图2所示，以G点为坐标原点，建立x轴过A点的分析坐标系，如图4所示，其中8个杆的长度分别为l₁，l₂，l₃，l₄，l₄，l₅，l₆，l₇，各杆件的水平夹角分别为α，βy，ε，θ，ξ，η。

1.3瓦特型六杆机构简化模型

为建立瓦特型六杆机构简化函数模型，将六杆机构拆分成一个四杆机构和一个二杆机构，如图5（a）、（b）所示。

2.目标优化层叠算法

目标优化层叠算法是指针对一个系统问题，需要把系统问题拆分为多个部分求解，首先对第一次部分进行优化，以第一部分的优化结果为基础再对系统问题的第二个部分进行优化，以此类推，直到完成系统问题最后部分的优化，最后判断所有部分的优化结果是否满足系统问题，满足则优化结束，否则返回第一部分再次优化，直到满足系统问题，如图6所示：为瓦特型六杆机构的优化算法流程图。

步骤1：初定四杆机构尺寸，设定其上、下限，通过E点实际值与计算值的函数关系建立目标函数，确定约束条件，优化四杆机构机构尺寸。

步骤2：由于ED杆长不变，D点运动轨迹与E点实际运动轨迹应该满足固定肋，建立目标函数，确定约束条件，优化二杆机构尺寸。

步骤3：修订六杆机构尺寸，当偏差足够小，完成优化，否则重复上述步骤。

3.计算实例

垂直搅拌器结构，如图7所示，为一铰链六杆机构.当安装于搅拌头（被引导件）7上的手柄H向下运动时，铰链中心D和E的运动轨迹分别为K_n和K_e当机构尺寸设计适当时，这两轨迹在搅拌器工作范围内近似直线且相互平行，因此，搅拌头7作近似直线平动，当搅拌头向下垂直运动到最下端，铰链D、E、F分别到达D、E、F位置.弹簧用于手柄日上撤去外力后使搅拌头回复至上端位置.构件4为机架，构件2和6均為连杆并分别与连杆1铰接，连杆2还与连杆5铰接，搅拌头7分别与构件6和8铰接于点D和E。

垂直搅拌器简化图，如图8所示，其中4、G与地面相连，依据A、B、c、D、E、F、G对应位置关系以及各杆件之问的相对位置可知，该六杆机构可以转化为Watt-I型六杆机构。

如图4所示，为搅拌器转化原理图.以G点作为坐标原点，建立坐标系，由于点E、F、B在一个杆件上，杆EFB可以看作一个刚性构建，转化为图4中的阴影三角形EFB，同理杆ABC转化为图4中的阴影三角形ABC，D点分别与E、C点相连接。

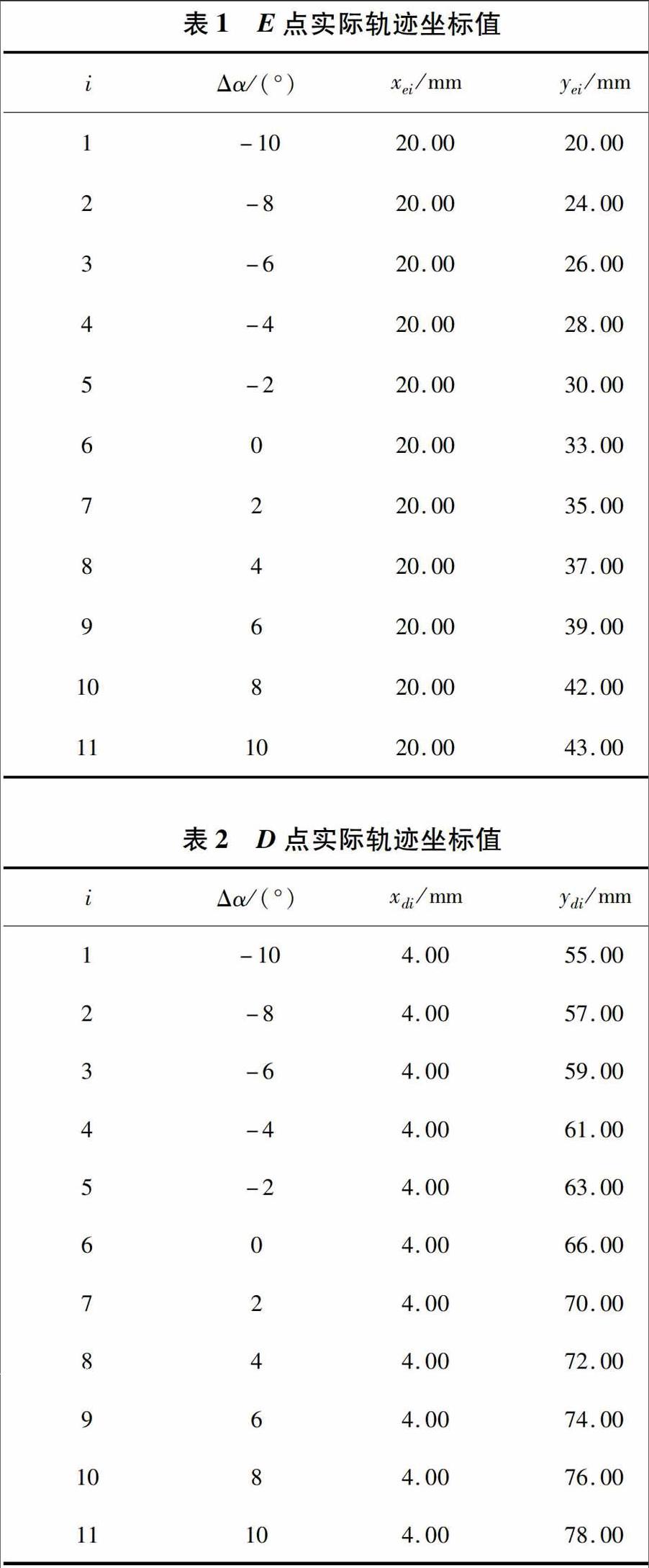
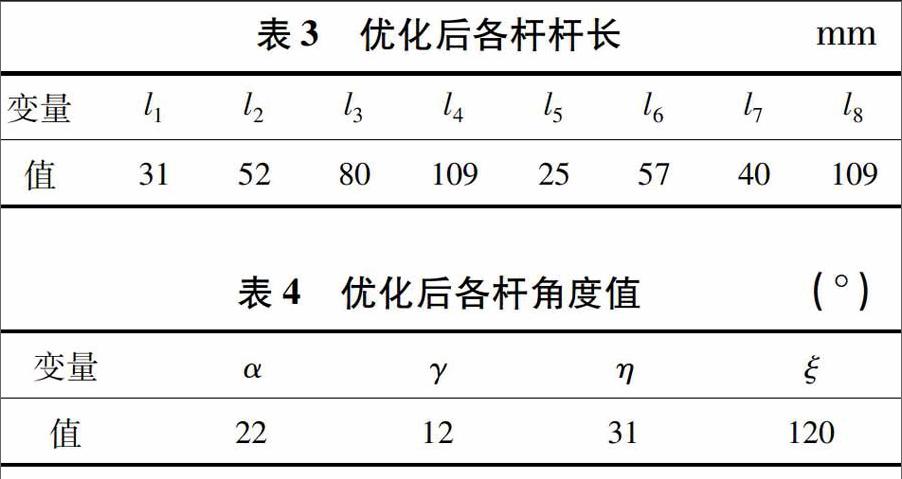
通过实际测量，可以获得E、D两点的实际坐标值.如表1所示，为E点实际轨迹坐标值，如表2所示，为D点实际轨迹坐标值。

依据本文提供的方法，将六杆机构拆分為四杆机构和二杆机构，采用目标优化层叠算法，首先对四杆机构进行优化，用Matlab编程，采用Matlab中fmincon函数。

[x，fval，exitflag，output]=fmincon（fun.X0，b，Aeq，beq，lb，ub）

其中fun为目标函数；XO为初始值，4、b满足线性不等式约束，Aeq、beq满足等式约束，lb、ub满足边界约束。

将式（11）、（12）、（13）代入fmincon函数，其中式（11）为目标函数，式（12）、（13）为约束条件。

编写Matlab程序，并运行.优化结束以后得到四杆机构的初始杆长，以此为基础对二杆机构进行优化，再次使用fmincon函数，将式（19）、（21）、（22）、（23）、（24）代入，fmincon函数中。

其中式（19）为目标函数，式（21）、（22）、（23）、（24）为约束条件。

再次编写Matlab程序，并运行.优化后得到二杆机构的杆长，以得到的六杆机构的所有杆长为基础对六杆机构进行总体优化。

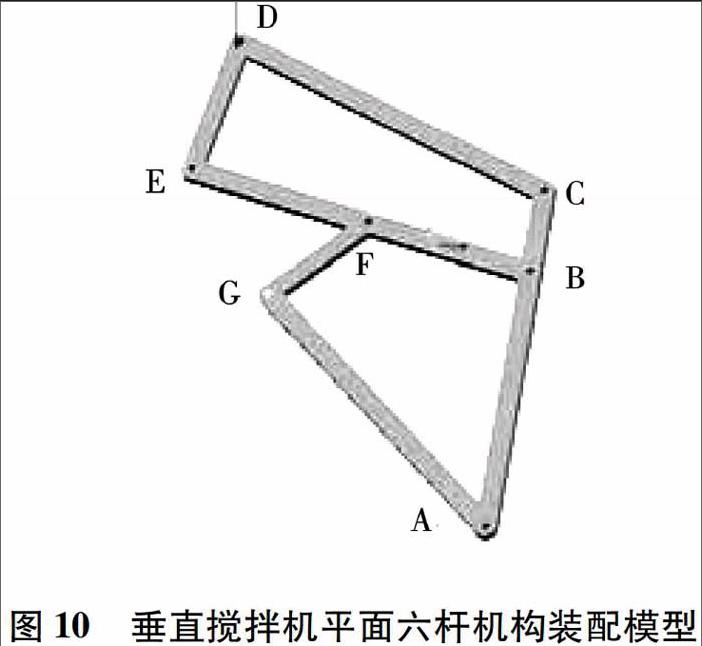
最终优化后得到的结果如表3、表4所示：

4.仿真分析

依据表3、表4得到的数据，运用proe绘制垂直搅拌机平面六杆机构并进行装配，装配图如图10所示。

AG杆与地面固定，在A、B、C、D、E、F、G点处添加转动副，在G点处添加伺服电动机，GF杆为驱动轴，定义运动周期为3s，对机构进行运动学仿真，在E、D点处添加轨迹曲线，来测量E、D点的运动轨迹，分别测量E点x坐标、y坐标随时问的变化曲线，D点x坐标、y坐标随时问的变化曲线。

将E、D点的仿真数据与实际数据进行对比分析，可以得到图13和图14，由图13、14可知D点仿真轨迹近似成一条直线，与实际轨迹近似平行，同时E点仿真轨迹近似成一条直线，与实际轨迹近似平行，由此可知六杆机构肋杆近似作垂直往复运动，从而实现了垂直搅拌机六杆机构的垂直往复运动。

由图13、14可知E、D两点在x轴方向存在摆动，最大摆动误差为0.15mm.在Y轴方向与实际值变化趋势一致，近似实现了E、D两点的轨迹。

将E、D两点的仿真值和实际值进行对比，建立表格，如表5、表6所示.在表5、表6中，△α（°）为杆1偏转角度，△X和△y分别为D点在X轴和y轴方向的偏移误差，（X_di，y_di）为D点的实际值，（X_Di，y_Di）为D点的仿真值.同理（X_ei，y_ei）为E点的仿真值，（X_ei，y_ei）为E点的实际值，△X和△y，分别为E点在x轴和y轴方向的偏移误差。

由表5可知在一个运动周期内，D点x轴方向产生的最大误差为0.15mm，Y轴方向产生的最大误差为0.30mm，误差较小，随着杆1偏转角度的增大，D点的误差呈增大的趋势，在行程极限位置处最大。

由表6可知在一个运动周期内，E点x轴方向产生的最大误差为0.15mm，y轴方向产生的最大误差为0.32mm，误差较小，随着杆1偏转角度的增大，E点的误差呈增大的趋势，在行程极限位置处最大.由表5、表6可知，E点和D点的误传变化趋势一致。

5.结论

1）本文提出层叠目标优化算法求解瓦特型六杆机构的函数综合算法，通过优化结果和仿真数据的对比分析表明，层叠目标优化算法用于求解六杆机构的函数综合正确有效。

2）本文提出了将瓦特型六杆机构拆分为四杆机构和二杆机构的方法，首先对四杆机构进行优化，在此类基础上优化二杆机构，最终实现六杆机构的优化，该方法减少了了优化过程中的未知变量，简化了优化过程，可以简单快速的实现瓦特型六杆机构的综合。

3）实例仿真分析的误差控制在0.4mm以内，近似实现了E、D点的垂直往复运动，证明本文提出的方法适用于求解瓦特型六杆机构优化问题，拓宽了瓦特型六杆机构函数综合法。